일반적으로 이용하는 행렬곱의 방법
[Math Processing Error]
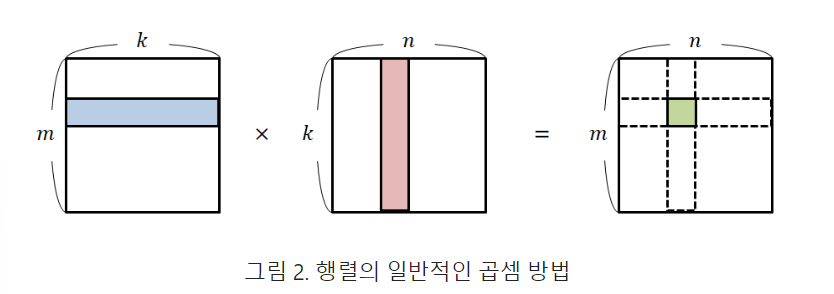
이것을 잘 뜯어 생각해보면, 왼쪽에 있는 행렬에서 행 하나를 가져오고 오른쪽에 있는 행렬에서 열 하나를 가져와서 계산하게 된다는 것을 알 수 있다.
행렬 곱이 이런 방식으로 정의되는 이유는 행렬이 일종의 함수라는 관점에서부터 얻어진다고 할 수 있다.
추후에 자세하게 다루겠지만, 행렬을 어떤 함수 [Math Processing Error]라고 생각해보자.
즉, 2 차원 벡터를 입력 받아 2차원 벡터를 출력하는 함수의 기능을 한다고 보자는 것이다.
다시 말해, 벡터 [Math Processing Error]와 아래의 행렬 [Math Processing Error], [Math Processing Error]에 대하여 (여기서는 mapping의 의미를 강조하여 [Math Processing Error]와 [Math Processing Error]로 씀)
[Math Processing Error][Math Processing Error]
각각의 매핑은 다음과 같다.
[Math Processing Error][Math Processing Error]
이 때 두 매핑의 합성 [Math Processing Error]를 생각해보면,
[Math Processing Error][Math Processing Error]
과 같다. 따라서 합성 매핑 [Math Processing Error]는 다음과 같이 정의되면 된다.
[Math Processing Error]
이 합성 매핑을 행렬의 곱으로 정의하고, 특별한 연산 기호는 쓰지 않고 두 행렬을 나란히 써서 나타낸다1.
또, 가져온 행 혹은 열을 벡터로 생각한다면 계산된 행렬의 각 원소값은 벡터의 내적을 표현한 것임을 알 수 있다.
즉, 식(1)의 계산 결과에서 1행 1열의 원소값은 계산 되기 전 두 행렬 중 왼쪽 행렬의 1행의 행벡터와 오른쪽 행렬의 1열의 열벡터를 가져와 계산한 것임을 알 수 있다.
열벡터의 선형 결합
다시 말해 행렬과 벡터의 곱은 행렬을 구성하고 있는 두 열벡터의 선형결합을 다른 방식으로 표현한 것이라고 할 수 있는 것이다.
열공간을 기반한 해석
벡터의 선형결합 부분에서 설명했던 것 처럼 벡터의 선형결합이 의미하는 것은 벡터 공간의 생성이다. 즉, 행렬과 벡터의 곱이라는 수식이 우리에게 묻는것은 “주어진 열벡터들을 이용해 만들 수 있는 벡터 공간(즉, 열공간(column space))에 대한 탐구”라는 점에서 매우 중요하다고 할 수 있다.