이 포스트는 The Byzantine Generals Problem - Leslie Lamport을 읽고 저만의 방식으로 정리한 글입니다.

Signed Message

앞서 살펴본 Oral Message 케이스와 달리 이번에는 배신자의 능력을 제한시킬 것인데, 그 방법으로 위조할 수 없는 사인이 된 메시지를 사용할 것이다. 앞의 Assumtions에 우리는 하나의 가정을 추가할 것이다.

• A4
  (a) 충실한 장교의 사인은 위조가 불가능하고, 내용을 변경하였을 시에는 바로 들킨다.
  (b) 아무나 사인의 authenticity(진실성)을 확인 가능하다.

사령관은 자신의 사인이 된 지시를 장교들에게 내리고, 장교들은 그 지시에 자신의 사인을 추가시켜서 나머지 장교들에게 또 전달한다. 이런 식으로 반복하는데, 이 때 지시의 내용은 변경이 불가능하다.

---

SM(m)

먼저 알아야 하는 것들

• choice

  choice 수는 지시의 집합에 적용되어서 하나의 값을 반환한다.

  1. 만약 집합 V가 하나의 원소 v(i)만 포함한다면 choice(V) = v(i)이다.

  2. 집합 V가 공집합이면 choice(V) = retreat(후퇴)이다.

• 집합 V

  집합 V(i)는 i번째 장교가 받은 지시의 집합이다. 주목해야 하는 점은 지시의 집합이지 메시지의 집합이 아니다. 즉, 사령관이 충실하다면, V는 하나의 원소만 포함하여야 한다. 같은 지시 내용에도 서로 다른 메시지는 있을 수 있다.

• v:i

  v:i는 v라는 값이 i번째 장교에게 사인되었는 것을 말한다.

알고리즘

태초에 모든 i에 대하여 V(i)는 비어있다.(공집합)

1. 사령관은 값에 자신의 사인을 하여서 모든 장교에게 전달한다.

2. 모든 i에 대하여,
   A. 만약 i번째 장교가 v:0의 형태의 메시지를 사령관으로부터 받았고, 이것이 처음 받은 지시라면,
   1) V(i) = {v},
   2) 다른 장교들에게 해당 지시에 자신의 사인을 추가한, v:0:i를 전달한다.

   B. 만약 i번째 장교가 v:0:j(1):j(2):...:j(k)의 형태의 메시지를 받았고, 이 지시가 V(i)에 포함되지 않는다면,
   1) 해당 지시 v를 V(i)에 포함한다.
   2) 만약 k<m 이면, v:0:j(1):j(2):...:j(k):i를 나머지 장교들에게 보낸다.

3. 모든 i에 대하여 i번째 장교가 더 이상 메시지를 받지 않을 때, 그는 choice(V(i)) 값을 따른다.

예로 알아보자.

해당 케이스는 SM(1), 사령관이 배신한 상황이다.

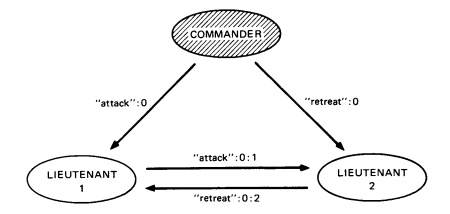
1. 배신한 사령관은 장교에게 각자 다른 지시를 사인하여 보낸다.
2A. 장교 1 입장에서 "attack":0이라는 지시를 처음 받았기 때문에, V(1) = {"attack"}이고, 장교 2에게 "attack":0:1을 전달한다.
2B. 장교 1 입장에서 "retreat":0:2이라는 형태의 메시지를 받았고, "retreat"이라는 지시는 V(1)에 포함되어 있지 않기 때문에, V(1).push("retreat"), V(1) = {"attack", "retreat"}이다. k=m=1이기 떄문에 2B(2)는 실행하지 않는다.

결과적으로, V(1) = V(2) = {"attack", "retreat"}이다. 일단 이 두상황에서 장교 1과 2는 사령관이 각기 다른 지시에 사인을 했다는 것을 가정 A4를 통해서 알 수 있고, 사령관이 배신하였다는 사실도 쉽게 밝혀낼 수 있다.

예를 보면 알 수 있듯이, 만약 SM(m)이라면, m-1번째 사인까지 메시지에 포함될 수 있고 m번째로 받은 사람은 사인을 하지 않고, 그냥 받는다.

---

증명

우리의 목표는 SM(m)이 장교의 숫자와 상관없이 최대 m명의 배신자가 존재 할때 비잔틴 장군 문제를 해결할 수 있다는 것을 보이는 것이다.(이 때 장교의 숫자는 최소 m+2명은 되어야 한다. 최소 2명의 충실한 장교가 있어야 비잔틴 장군 문제를 푸는 것이 의미가 있기 때문이다.)

Theorem 2

모든 m에 대하여, 최대 m명의 배신자가 있을 때 SM(m)은 비잔틴 장군 문제를 풀 수 있다.

증명

1. 먼저 IC2를 보이자.
   사령관이 충실할 때, 사령관은 자신의 사인이 포함된 지시 v:0을 모든 장교에게 보낸다. 모든 장교는 2A에서 이 지시를 받는다. 아무리 배신한 장교라고 해도, 지시의 내용을 변경할 수 없기 때문에(A4), 모든 충실한 장교의 V = {v}이고, 결국 choice(V) = v로 사령관의 지시를 따르게 된다.
   
   

2. IC1을 보이자. 사령관이 충실한 경우에는 IC1이 IC2를 자동으로 따라가기 때문에, 우리는 사령관이 배신한 경우만 고려하면 된다.

   IC1을 만족하려면 모든 장교는 같은 지시를 따라야 한다. 우리의 알고리즘을 살펴보면 어느 장교 i와 장교 j가 같은 지시를 따르려면 같은 지시의 집합, V(i) = V(j)를 만족하면 된다. 만약, 장교 i가 2번 과정에서 지시 v를 추가했다면, 장교 j도 2번 과정에서 지시 v를 추가하여야 한다. 각 케이스를 살펴보자.

   a. 장교 i가 지시 v를 2A에서 받았을 때

   그렇다면, 장교 i는 지시 v를 2A(2)에 의해서 다른 장교들에게 보내고, 이 때 장교 j도 받을 것이다.

   b. 장교 i가 지시 v를 2B에서 받았을 때

   그렇다면, 장교 i는 v:0:1:2:...:k의 형태의 메시지에 새로운 지시 v를 받았다는 말이다. 만약 장교 j가 (0~k)에 포함된다면, 장교 i가 받기 전에 이미 장교 j는 해당 지시를 받았을 것이다. 만약 포함되지 않는다면,

   1. k < m
      이 때 2B(2)에 의하여 장교 i는 v:0:1:2:...:k:i를 (0~k)에 포함되지 않는 장교들에게 보낼 것이고, 이 때 장교 j도 수령할 수 있다.
   2. k = m
      이 때 사령관이 배신하였기 때문에, 장교들 사이에는 최대 (m-1)명의 배신자가 존재한다. k = m이므로 (0~k) 사이에는 최소 한명의 충실한 장교가 존재한다. 그렇다면, 이 최소 한명의 충실한 장교는 해당 메시지를 수령하였을 때, 다른 충실한 장교에게도 전파하였을 것이기 때문에, 장교 j도 받았을 것이다.