[풀잎스쿨] CS231n 3강(1) Loss Functions

데이터 여행자·2021년 1월 8일

[AIFFEL 대전 1기] 학습일지

목록 보기

9/42

스탠퍼드 대학의 CS231n: Convolutional Neural Networks for Visual Recognition
본 포스팅은 CS231n 3강의 내용을 정리한 것이다. 이곳에 출처가 따로 언급되지 않은 이미지들은 스탠퍼드 대학에서 제공하는 강의 슬라이드에서 가지고 왔다.

[CS231n] http://cs231n.stanford.edu/2017/syllabus.html

지난 시간 복습

Loss Funcion(손실 함수) 는 가중치 $W$ 이 얼마나 나쁜지를 정량적으로 보여주는 함수이다. 즉 가중치 $W$ 를 사용해서 나온 예측 점수에 대해 불만족의 정도를 숫자로 나타내는 것이 손실함수이다. 따라서 Loss가 작을 때 그 분류기는 이미지를 잘 분류함을 알 수 있다.

Optimization(최적화) 는 손실함수를 최소화할 수 있는 parameter를 찾는 방법이다. 다시 말하면, 어떤 $W$ 가 Loss를 가장 적게 하는가를 보여주는 것이며, (실제값-Loss)의 간격을 최적화를 통해 줄일 수 있다.

손실 함수

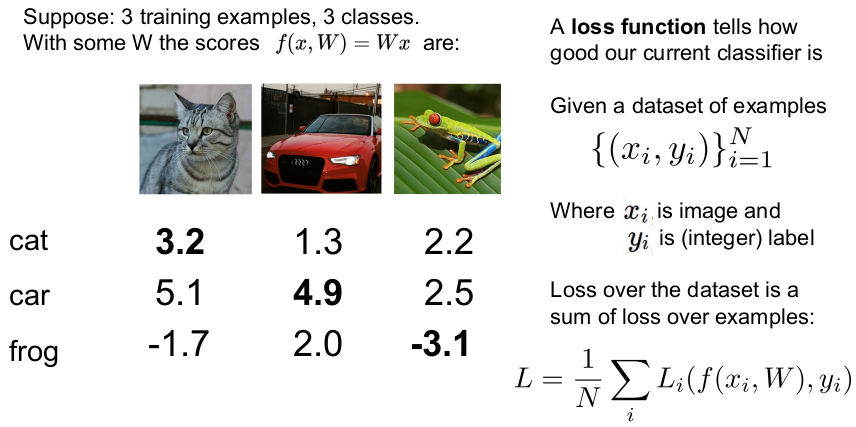
여기서 $x_i$ 는 입력 이미지이고 $y_i$ 는 예측 레이블(타겟)이다. 총 Loss는 데이터에 대한 각각의 Loss의 평균값이다.

이 강의에서는 Loss의 2가지 예를 살펴본다. Multiclass SVM(Support Vector Machine) 을 이용한 Multiclass SVM loss(Hinge loss) 와 Softmax function 을 이용한 Cross entropy loss 이다. 우선 Multiclass SVM loss를 살펴보자. (Multiclass SVM loss는 2개의 클래스를 다루는 SVM을 일반화한 것이다.)

Multiclass SVM loss

SVM loss는 위의 식으로 계산할 수 있다. 식에서 $s_j$ 는 이미지에 대한 오답 클래스의 예측 점수이고 $s_{y_i}$ 는 정답 클래스의 예측 점수이다. 1 은 Safty margin 이라고 불린다. Multiclass SVM Loss는 점수간 상대적인 차이에 중점을 두기 때문에 margin의 크기는 사실 어떤 것이든 상관 없다. 이에 대한 자세한 설명은 온라인 코스 노트를 참고하면 된다.

safty margin은 정답 클래스의 예측 점수가 다른 클래스의 예측 점수보다 최소 얼마나 더 커야하는지 정해준다. 정답 점수가 다른 점수에 비해 safety margin만큼 크지 않으면 loss가 생길 수 있다. safety margin이 1일 때, (정답 클래스의 예측 점수-오답 클래스의 예측 점수)이 1보다 크면 loss가 생긴다는 뜻이다.

Multiclass SVM loss는 그래프의 모양이 경첩같이 생겨서 Hinge loss 라고 부르기도 한다. 정답인 클래스의 예측 점수가 오답인 클래스의 예측 점수보다 크면 Hinge Loss는 작아진다. (loss가 커지면 이미지를 잘 분류하지 못하고, loss=0이라면 이미지를 잘 분류한다는 뜻).

3개의 클래스를 갖는 3개의 학습 데이터를 가정하고, W는 Linear Classifier를 따른다고 해보자. Hinge loss를 직접 계산해 보면 아래와 같다.

Cat 이미지: $L1 = max(0, 5.1-3.2+1) + max(0, -1.7-3.2 +1)= max(0, 2.9) + max(0, -3.9) = 2.9 + 0 = 2.9$
Car 이미지: $L2 = max(0, 1.3-4.9+1) + max(0, 2.0-4.9+1)= max(0, -2.6) + max(0, -1.9) = 0 + 0 = 0$
Frog 이미지: $L3 = max(0, 2.2-(-3.1)+1) + max(0, 2.5-(-3.1)+1)= max(0, 6.3+1) + max(0, 6.6) = 6.3 + 6.6 = 12.9$

각 클래스의 Loss의 평균은 5.27로, 이 이미지 분류기는 이미지를 잘 분류하지 못한다고 볼 수 있다. Loss가 0에 가까울수록 이미지를 잘 분류하는 것이기 때문이다.

Q1. 자동차의 점수를 조금 바꾸면 Loss는 어떻게 되는가?

변화가 없다. 자동차 클래스(정답 클래스)의 크기가 다른 오답 클래스의 점수보다 크기 때문에 Loss는 변함 없이 0이 된다. 그러나 만약 자동차의 점수가 2.0 이하(크게 변화)라면 Loss에 변화가 생긴다. (이해가 안 된다면 직접 수를 넣어 계산해 보자.)

Q2. Loss의 최대값, 최소값은 무엇인가?

정답 클래스의 점수가 클 때 Loss는 최소값인 0이 되고, 정답 클래스의 점수가 (이론상) 아주 큰 음수라면 Loss의 최대값은 $∞$ (무한대)가 된다.

Q3. 일반적으로 가중치 W를 매우 작은 값으로 초기화한다. 그 때 모든 s는 0에 가깝게 된다. 이런 상황에서 Loss의 값은 무엇인가?

(클래스 수 - 1) (계산을 직접 해보면 알 수 있다.)

디버깅 전략(Sanity Check): $W$ 를 처음 학습할 때 Loss ≠ (클래스 수 -1)라면 버그가 걸렸다는 것을 알 수 있다.

Q4. Loss 구하는 식이 정답을 포함한다면 Loss는 어떻게 될까?

Loss + 1이 된다. (직접 계산해 보자.)

Q5. 합 대신에 평균을 사용하면 어떻게 될까?

Loss는 영향을 받지 않는다. Multiclass SVM loss function에서는 점수가 중요한 것이 아니라 점수의 상대적인 차이를 중요시 한다. 따라서 합 대신 평균을 사용하는 것은 점수의 차이를 단지 rescaling하는 것 뿐이다.

Q6. Loss를 구하는 식이 위의 식과 같이 된다면 어떻게 되는가?

Loss function 값이 완전히 달라진다. (이 Loss function을 Squared Hinge Loss라고 부른다.) 오답 클래스의 Loss가 나쁜 것은 더 나쁘게 되는, 좋은 것은 더 좋게 만드는 등 상황이 달라진다. 따라서 어떤 Loss function을 설계하는지가 중요하다.

결론적으로 이미지 분류기가 이미지를 잘 분류한다면 Loss=0이 된다. 그렇다면 Loss=0인 가중치 $W$ 가 유일할까?

이에 대한 대답은 '아니다'이다. 아래의 그림에서 보듯 2 $W$ 역시 Loss=0이 된다.

위의 식에서 L=0이 되는 $W$ 를 고르는 것은 좋지 않다. 그 이유는 training data에만 맞는(fitting) Loss function만 찾는 것이기 때문이다. 이 경우, test data를 넣었을 때 이미지 분류기가 이해하지 못할 행동을 할 수 있다.

Regularization

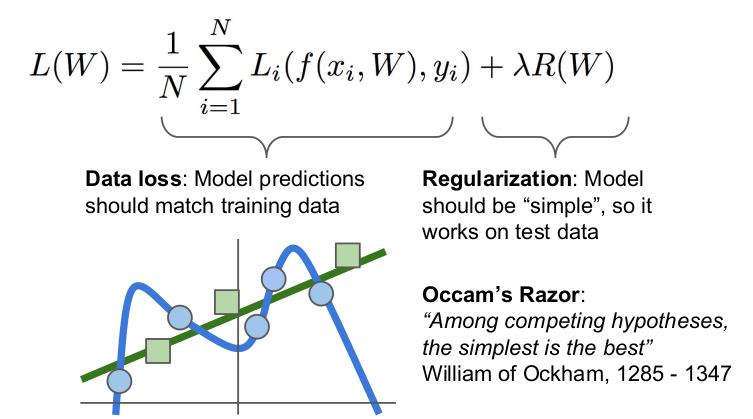
우리는 test data에 관심이 있는데 위의 그림에서 파란색 선은 새로운 data를 잘 설명해주지 못한다.

위의 식에서 Data loss 는 training data에 최적화된 예측 모델을 찾고, Regularization 은 test data에 적합하도록 일반화된 예측 모델을 찾는다. 비슷한 가설이면 간단한 것이 최고라는 오컴의 면도칼 이론처럼 예측 모델은 일반화되고 단순한 것이 좋다. Loss=0이면 training data에 너무 딱 맞아서(overfitting) 새로운 데이터에는 적용되지 않는다. 따라서 우리는 파란색 선보다 일반화되고 단순한 초록색 선을 더 선호한다. 초록색 선을 만들기 위해 Regularization을 Loss function에 넣어준다. Regularization은 예측 모델( $W$ )이 복잡한 고차 다항식을 선택할 때 페널티를 줌으로써, 단순한 저차 다항식을 선택하도록 만든다.

다시 말하면 Regularization은 예측 모델(W)이 training data에 완전히 fit하지(overfitting) 못하게 모델 복잡도에 패널티를 부여하는 것이다. loss function에 Regularization이 들어가면 training error는 더 커지지만 우리의 목적인 test data의 결과는 좋아진다.

data loss는 training data에 맞는 $W$ 를 찾고, Regularization은 test data를 잘 설명할 수 있는 일반화된 $W$ 를 찾으려고 한다. data loss와 Regularization은 서로 경쟁을 하면서 data loss와 Regularization에 최적화된 $W$ 를 찾는다. (a way of trading off data loss and regularization on test set)

위의 것들은 Regularization에 사용되나 일반적으로 Regularization으로 L2를 많이 사용한다. 참고로 Deep learning에 최적화된 것은 Dropout, Batch normalization, Stochastic depth이다.

참고: 딥러닝 용어 정리, L1 Regularization, L2 Regularization 의 이해, 용도와 차이 설명
L1이 sparse모델에 적합한 이유

Linear Classifier의 함수 $f(x,W)=xW$ 와 같이, 4열 벡터에 서로 다른 가중치 $W_1$ , $W_2$ 를 내적하면 둘 다 결과는 1이 나온다. $W_1$ 의 경우, 첫번째 원소 외에 다른 원소들은 무시하지만 $W_2$ 는 모든 원소들을 골고루 반영한다.

$L1$ 의 경우는 $W_1$ 을 더 선호한다. L1은 W에서 0의 갯수에 따라 모델 복잡도가 달라지며(복잡도: $W$ 의 0이 아닌 수의 갯수), $W$ 의 원소를 대부분 0이 되게 한다. 이를 sparse solution이라고 한다. 반면, $L2$ 는 $W_2$ 를 선호한다. L2의 Regularization는 x의 모든 원소가 골고루 영향을 미치게 한다. 이를 coarse solution이라고 한다. L2는 $W$ 의 feature를 최대한 고려하며, 동일한 점수라면 더 넓게 펼쳐져 있는 것을 선호한다. 숫자가 넓게 퍼질 때, 모델 복잡도는 덜 복잡해진다.

복잡도는 문제에 따라 달라지므로 모델에 맞춰 선택해야 한다.

Softmax Classifier

Softmax는 또다른 Classifier이다. 이것 역시 이항의 Logistic Regession을 다차원으로 일반화시킨 것이다.

Multiclass SVM Loss는 예측 점수 자체는 고려하지 않고, 정답 클래스의 예측 점수가 오답 클래스의 예측 점수보다 크기만을 바란다. 그러나 Softmax는 클래스별 확률분포를 사용하여 예측 점수 자체에 추가적인 의미를 부여한다.

Softmax Classifier에서 사용하는 Loss는 Cross entropy loss 라고 하며, 정답이 나올 확률의 최소값을 의미한다(음수는 확률을 구할 수 없기 때문). 즉 Loss $=-log$ (정답 클래스가 정답일 확률)이다. (log는 지수와 반대되는 개념이므로 취해준다. loss의 정의가 $W$ 가 얼마나 나쁜지에 대한 것이므로 -를 붙인다.)

Softmax Classifier는 예측 점수를 지수화하여(확률로 나타내기 위하여) 점수를 양수로 만들고, 정규화를 시켜 확률분포로 만든다. 정규화시켰으므로 0.13, 0.87, 0.00, 이 세 수의 합은 1이다. 우리의 관심인 정답 클래스가 정답일 확률은 0.13.이고 cross entropy loss는 0.89이다.

예를 들어 고양이 이미지를 고양이로 분류하면 고양이 클래스일 확률은 1이고 나머지 클래스의 확률은 0이다. Softmax classifier는 정답 클래스가 정답일 확률을 1(loss=0)에 가깝게 만들려고 한다.

Q1. Cross entropy loss의 최소, 최대값은?

0부터 무한대까지( $-logx$ 의 치역을 보자).
최소값은 정답일 확률이 1일 때이고, 최대값은 정답이 아닐 확률 0일 때이다.

최소값(정답일 경우): $-log(1) = 0$ , 즉 Loss = 0, 스코어는 무한대
$-log(0) = -(-∞) = ∞$
그러나 유한정밀도를 가지고는 $∞$ 를 얻을 수 없다. 이런 일은 발생하지 않는다.

Q2. W를 처음 학습할 때 주로 W는 작게 설정하기 때문에 모든 s는 0에 가깝게 된다. 그 때 Loss의 값은 무엇인가?

Loss = $-log(\frac{1}{C})$ = $log(C)$
디버깅 전략(sanity check): 첫번째 iteration에서 Loss $≠ log(C)$ 라면 버그가 걸린 것이다.

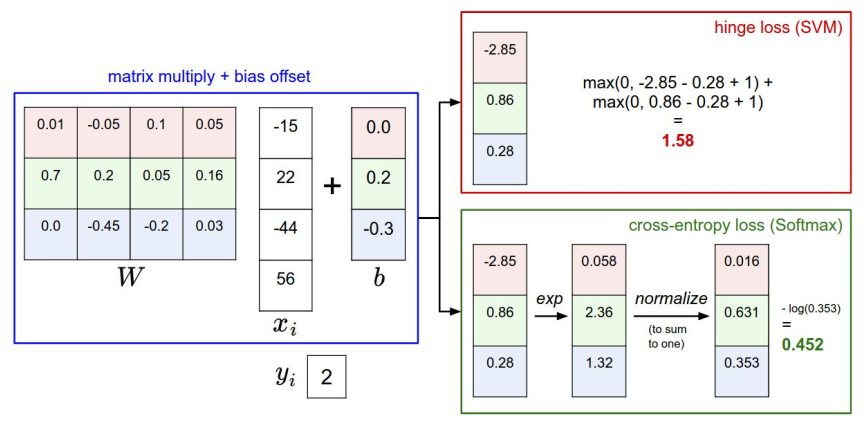
두 Loss function을 비교한 그림이다. 둘 다 예측 점수는 같으나 예측 점수를 해석하는 방법이 다르다. Multiclass SVM은 정답 클래스의 예측 점수와 오답 클래스의 예측 점수의 차이를 중요시 하고, Softmax는 예측 점수 자체를 해석하고자 한다.

Q. 예측 점수를 조금 변화시킨다면 각각의 함수에서 Loss는 어떻게 될까?

SVM은 예측 점수 자체보다 정답 클래스의 예측 점수와 오답 클래스의 예측 점수의 차이에 관심을 두기 때문에 Loss는 변하지 않지만(둔감) Softmax는 정답 클래스의 예측 점수를 확률로 만들기 때문에 Loss는 변한다(민감). 그러나 예측 점수가 많이 변한다면 Hinge Loss도 변화한다.