[GD-P2] 머신러닝 모델 정리

Complement Naive Bayes Classifier(CNB)

많은 샘플이 특정 클래스에 치우져 있을 경우에 사용. 가중치를 부여하여 나이브 베이즈 분류기를 보완했기 때문에 나이브 베이즈 분류기보다 성능이 좋다.

• 참고: 나이브 베이즈 분류기는 각 데이터가 조건부로 독립적이라는 가정을 한다. 따라서 많은 데이터가 특정 클래스에 치우져서 속해있다면 모델은 특정 클래스를 선호한다.

Logistic Regression

가장 널리 알려진 선형 분류 알고리즘. 소프트맥스(softmas) 함수를 사용한 다중 클래스 분류 알고리즘이며, 다중 클래스 분류를 위한 로지스틱 회귀를 소프트맥스 회귀(Softmax Regression)라고도 한다. 이름은 회귀지만, 실제로는 분류를 수행한다.

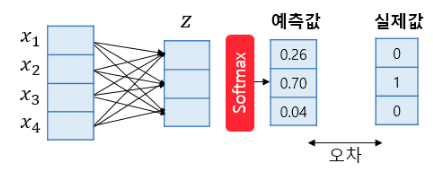
• 소프트맥스 함수: 클래스가 N개일 때, N차원의 벡터가 각 클래스가 정답일 확률을 표현하도록 정규화를 해주는 함수.

위의 그림은 4차원의 벡터를 입력으로 받아 3개의 클래스를 예측하는 경우의 소프트맥스 회귀의 동작 과정을 보여준다. 3개의 클래스 중 1개의 클래스를 예측해야 하므로 소프트맥스 회귀의 출력은 3차원의 벡터고, 각 벡터의 차원은 특정 클래스일 확률이다. 오차와 실제값의 차이를 줄이는 과정에서 가중치와 편향이 학습된다.

SVM(Support Vector Machine)

대표적인 선형 분류 알고리즘.

- 2 차원 공간에서, 즉 데이터에 2개의 클래스만 존재할 때

• Decision Boundary(결정 경계): 두 개의 클래스를 구분해 주는 선
• Support Vector: Decision Boundary에 가까이 있는 데이터
• Margin: Decision Boundary와 Support Vector 사이의 거리

Margin이 넓을수록 새로운 데이터를 잘 구분할 수 있다. Margin 최대화 -> robustness 최대화

• Kernel Trick: 저차원의 공간을 고차원의 공간으로 매핑해주는 작업. 데이터의 분포가 Linearly separable 하지 않을 경우 데이터를 고차원으로 이동시켜 Linearly separable하도록 만든다.

• cost: Decision Boundary와 Margin의 간격 결정. cost가 높으면 Margin이 좁아지고 train error가 작아진다. 그러나 새로운 데이터에서는 분류를 잘 할 수 있다. cost가 낮으면 Margin이 넓어지고, train error는 커진다.

• $\gamma$: 한 train data당 영향을 미치는 범위 결정. $\gamma$가 커지면 영향을 미치는 범위가 줄어들고, Decision Boundary에 가까이 있는 데이터만이 선의 굴곡에 영향을 준다. 따라서 Decision Boundary는 구불구불하게 그어진다. (오버피팅 초래 가능) 작아지면 데이터가 영향을 미치는 범위가 커지고, 대부분의 데이터가 Decision Boundary에 영향을 준다. 따라서 Decision Boundary를 직선에 가까워진다.

많은 선형 분류 모델은 대부분 이진 분류 모델이다. 그런데 이진 분류 알고리즘을 일대다(one-vs.-rest 또는 one-vs.-all) 방법을 사용해 다중 클래스 분류 알고리즘으로 사용할 수 있다. 일대다 방식은 각 클래스를 다른 모든 클래스와 구분하도록 이진 분류 모델을 학습시킨다. 클래스의 수만큼 이진 분류 모델이 만들어지고 예측할 때는 만들어진 모든 이진 분류기가 작동하여 가장 높은 점수를 내는 분류기의 클래스를 예측값으로 선택한다.

• 참고
  [머신러닝] SVM (서포트 벡터 머신)
  머신러닝 - 2. 서포트 벡터 머신 (SVM) 개념
  서포트 벡터 머신(Support Vector Machine) 쉽게 이해하기

결정 트리(Decision Tree)

결정 트리는 분류(범주형)와 회귀(연속형) 모두 가능한 지도학습 모델. 특정 기준(질문)에 따라 데이터를 구분하는 모델. 한 번의 분기 때마다 변수 영역을 2개로 구분한다.

• 노드(Node): 질문이나 정답을 담은 네모 상자
• Root Node: 맨 처음 분류 기준
• Terminal Node / Leaf Node: 맨 마지막 노드
• 각 terminal node에 속하는 데이터의 개수를 합하면 root node의 데이터수와 일치한다.

과정

데이터를 가장 잘 구분할 수 있는 기준으로 데이터를 나눈다. 나뉜 각 범주에서 데이터를 가장 잘 구분할 수 있는 질문을 기준으로 데이터를 나눈다. 이 방식을 계속 한다.

가지치기(Pruning)

데이터를 계속 나누다보면 오버피팅이 되기 때문에 최대 깊이나 터미널 노드의 최대 개수를 제한한다.

• min_sample_split: 한 노드에 들어 있는 최소 데이터의 수 결정
• max_depth: 최대 깊이 결정

Entropy, Impurity

• 불순도(Impurity): 해당 범주 안에 서로 다른 데이터가 얼마나 섞여 있는지를 보여준다. 한 범주에 한 데이터만 있으면 불순도가 최소이고 한 범주 안에 서로 다른 데이터가 정확히 반반 있으면 불순도가 최대가 된다. 결정트리는 불순도를 최소화하는 방향으로 학습한다.

• 엔트로피(Entropy): 불순도를 수치적으로 나타낸 척도. 엔트로피가 높으면 불순도가 높다. 엔트로피가 1이면 불순도가 최대, 0이면 불순도는 최소이다.

Entropy = $- \sum_i (p_i)log_2(p_i)$

($p_i$: 한 영역 안에 존재하는 데이터 가운데 범주 i에 속하는 데이터의 비율)

정보 획득(Information gain)

분기 이전의 엔트로피에서 분기 이후의 엔트로피를 뺀 수치. 결정 트리는 정보 획득을 최대화하는 방향으로 학습한다. 어느 feature의 어느 분기점에서 정보 획득이 최대화되는지 판단해서 분기가 진행된다.

Information gain = entropy(parent) - [weighted average]entropy(children)

트리 계열 모델은 고차원이고 희소한 데이터에 대해 성능이 나오지 않는다.

• 참고
  머신러닝 - 4. 결정 트리(Decision Tree)

랜덤 포레스트(Random Forest)

랜덤 포레스트는 여러 개의 결정 트리를 모아 만든 모델이다. 결정 트리는 훈련 데이터에 오버피딩을 되기 쉽기 때문에 랜덤 포레스트를 통해 오버피팅을 방지할 수 있다.

과정

n개의 요소(feature) 중 랜덤으로 i 개의 feature만 선택해 하나의 결정트리를 만들고, 또 랜덤으로 i 개의 feature를 선택해 또 하나의 결정 트리를 만드는 방식을 반복해 여러 개의 결정 트리를 만든다. 각 결정 트리마다 내놓은 하나씩의 예측값 중 가장 많이 나온 값(분류) 또는 평균값(회귀)을 최종 예측값으로 정한다. 이렇게 의견을 통합하거나 여러 결과를 합치는 방식을 앙상블(Ensemble)이라고 한다.

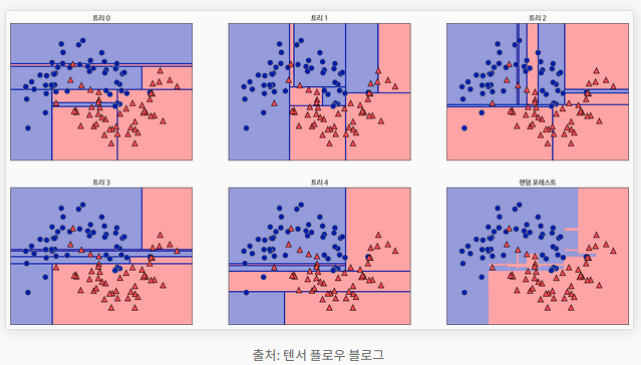
[랜덤 포레스트의 시각화]

Bagging

Baggin은 트리를 만들 때 training set의 부분집합을 활용해 형성하는 것이다. 즉 1000개의 데이터가 존재하면 각 트리를 생성할 때 100개의 데이터만 임의로 선택해 트리를 만들 때 활용한다. 여기서 중요한 것은 데이터를 임의로 선택할 때 중복을 허용한다는 것이다. 따라서 데이터를 많이 뽑아도 unique한 데이터셋을 형성할 수 있다.

파라미터

• n_estimators: 랜덤 포레스트 안의 결정 트리 갯수, 클수록 좋지만 메모리와 훈련 시간이 증가한다.

• max_features: 무작위로 선택할 feature의 갯수, max_features가 크면 트리들이 비슷해지고, 작으면 달라진다. 일반적으로 default를 쓴다.

• 참고
  머신러닝 - 5. 랜덤 포레스트(Random Forest)
  Random Forest(랜덤 포레스트) 개념 정리

그래디언트 부스팅 트리(GradientBoostingClassifier)

앙상블

• 부스팅: 랜덤 포레스트
• 배깅: AdaBoost, Gradient Boost 등
• Gradient Boost의 변형 모델: XGBoost, LightGBM, CatBoost

회귀와 분류에 모두 사용할 수 있는 모델. 여러 결정트리를 묶어 강력한 모델을 만드는 앙상블 기법. 하나의 leaf(타겟 값에 대한 초기 추정값)에서 시작. 보통 초기 추정값은 평균이다. tree의 error는 다음 tree에 영향을 준다. 보통 leaf의 개수는 8~32개이다.

얕은 트리 같은 간단한 모델을 많이 연결하는 모델. 각 트리는 데이터의 일부만 잘 예측하므로 트리가 많을수록 성능이 좋아진다.

그레디언트 부스팅 트리는 이전 트리의 오차를 보완하는 방식으로 순차적으로 트리를 만든다. 무작위성이 없고, 강력한 사전 가지치기가 사용된다. 또한 그래디언트 부스팅 트리는 일부 특성을 무시한다는 특징이 있어서 보통 랜덤 포레스트를 먼저 사용해보고, 성능이나 예측 시간 면에서 만족스럽지 않은 경우에 그래디언트 부스팅 트리를 시도해보는 것이 좋다.

일반적으로 1 ~ 5 정도의 트리를 사용하므로 메모리도 적게 사용하고 예측도 빠르다. 정확도도 준수하고, 예측 속도가 빨라 데이터 경진 대회에서 많은 우승을 했다. 훈련 시간의 속도가 좀 오래 걸리고 희소한 고차원 데이터에 대해서는 잘 동작하지 않는다는 단점이 있다.

• 참고
  머신러닝 - 15. 그레디언트 부스트(Gradient Boost): 과정이 자세히 설명되어 있으므로 나중에 살펴볼 것.
  [지도학습] 의사결정나무/랜덤포레스트/그래디언트 부스팅
  : 간략한 설명, 원리, 장단점을 잘 설명했으므로 나중에 살펴볼 것!

보팅(Voting)

앙상블 학습

여러 개의 분류기를 생성하고 그 예측값을 결합하여 1가지 분류기를 사용할 때보다 정확한 예측을 도출하는 기법이다.

성능(강력한 모델) < $\sum_n$ 성능(약한 모델)

앙상블 학습 유형

보팅(voting)

• 투표를 통해 최종 예측 결과 결정
• 서로 다른 알고리즘 결합
• 보팅의 종류
  • 하드보팅(hard voting): 다수의 분류기가 예측한 결과값을 최종 결과로 선정
  • 소프트보팅(soft voting): 최종 결과물이 나올 확률값을 다 더해서 최종 결과물에 대한 각각의 확률을 구한 뒤 최종값 도출

배깅(bagging)

• 데이터 샘플링(bootstrap)을 통해 모델을 학습시켜 결과를 집계
• 같은 유형의 알고리즘 사용
• 데이터 분할 시 중복 허용
• 과적합 방지에 효과적

부스팅(boosting)

• 여러 개의 분류기가 순차적으로 학습 수행

• 이전 분류기가 예측이 틀린 데이터를 올바르게 예측하도록 다음 분류기에서 가중치를 부여하면서 학습과 예측 진행

• 예측 성능이 뛰어나 앙상블 학습 주도

• 속도가 느리고 과적합 발생 가능성 존재

• 참고: 머신러닝 앙상블(Ensemble) 학습

로이터 데이터 사용시 모델별 성능 비교(정확도)

• Naive Bayes Classifier: 65%
• Complement Naive Bayes Classifier: 77%
• Logistic Regression: 약 81%(80.7%)
• SVM: 78%
• Decision Tree: 62%
• Random Forest: 67%
• GradientBoostingClassifier: 76%
• voting: 81%
  (Logistic Regression, Complement Naive Bayes Classifier, GradientBoostingClassifier 사용, soft voting)

-> 최종 결과: voting!