logit, 확률, sigmoid, softmax

sigmoid 함수 - activation function

인공신경망에서 ReLU함수 이전에 주로 사용되었던 activation function(활성화 함수)이며, hidden 노드 바로 뒤에 부착한다.

$sigmoid = \frac {1}{1+e^{-x}} = \frac {e^x}{e^x + 1}$

[출처: 위키피디아]

softmax 함수 - classification

인공신경망이 결과로 내놓은 K개의 클래스를 확률처럼 해석하도록 만들어 준다. 함수의 범위가 [0, 1]이기 때문이다. 따라서 output 노드 바로 뒤에 부착된다.

$softmax = \frac{exp(t_i)}{\sum^K_{j=1} exp(t_j)}$

logit

logit은 이진 분류 문제(binary classification)이다. y가 $C_1$으로 분류될 확률이라면 $C_2$으로 분류될 확률은 1-y이다. (확률의 총합은 1이고, 이진 분류이기 때문)

$P(C_1|x) = y, P(C_2|x) = 1-y$ 일 때, $y > 0.5$이면 $C_1$, $y \leq 0.5$이면 $C_2$이다.

이를 식으로 표현하면 $\frac {y}{1-y}$이고 이를 odds 라고 한다. odds가 1보다 크면(y>1-y) $C_1$, 1보다 작으면(y<1-y) $C_2$이다. (odds는 실패비율 대비 성공비율이고, odds가 클수록 성공확률이 더 크다는 뜻이다. odds값의 범위는 [0, $\infin$]이다.)

odds에 log를 씌우면 결정의 기준이 0으로 바뀐다. (log1 = 0이므로) 이를 식으로 표현하면 $log \frac {y}{1-y}$이고, logit (logistic + probit)이라고 부른다.

[logit 함수, 출처: 위키피디아]

logit 변환은 [0, 1]의 범위를 가지는 확률을 [-$\infin$, $\infin$]로 바꿔주는 변환이다. 따라서 예측값(y)과 예측값을 만들어내는 특성값(x)의 관계를 선형 관계(y = wx+b)로 만들 수 있게 한다. y의 범위는 [0, 1]이고, 특성값 x의 범위는 [-$\infin$, $\infin$]이므로 관계를 말할 수 없지만 logit 변환을 사용하면 두 값의 관계를 말할 수 있고, 이로 인해 로지스틱 회귀식을 사용할 수 있게 된다.

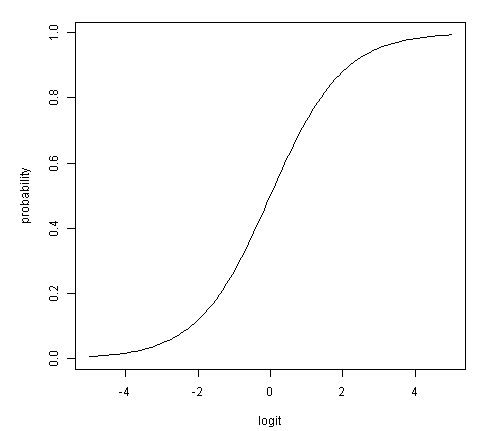
[확률과 logit의 비선형 관계, 출처: 로짓(Logit) 이란?]

그러나 분류를 하는 딥러닝에서는 확률화되지 않은 예측 결과를 logit이라고 한다. 확률값을 계산하지 않고 layer를 거쳐 나온 산출물을 그대로 다음 layer에 넘길 때 사용한다. 다시 말하면, logit은 신경망의 최종 레이어가 내놓는 확률값이 아닌 결과이고, 결과값의 범위가 [-$\infin$, $\infin$]이다. 따라서 양수인지, 음수인지에 따라서 클래스를 구분할 수 있다(이진 분류). 다중 분류 문제에서 logit은 보통 Softmax 함수의 입력으로 사용된다. Softmax 함수는 신경망의 결과를 확률로 바꿔준다.

[출처: https://chacha95.github.io/2019-04-04-logit/]

참고: tensorflow의 loss 함수에서의 from_logit
Binary_crossentropy나 Categorical_corssentropy 함수에서는 from_logits 인자를 설정할 수 있다.

모델이 해당 클래스의 범위에서 확률을 출력하면 logit=False, 모델의 출력값이 sigmoid 또는 linear를 거쳐 확률이 아닌 값이 나오면 logit=True이다.

logit, sigmoid, softmax의 관계

• logit - sigmoid: 역함수 관계
• logit - softmax
  • logit: 신경망의 결과값, [-$\infin$, $\infin$]의 범위
  • softmax: logit을 입력으로 받아 확률값([0, 1])으로 변화시킴
• sigmoid - softmax
  sigmoid와 softmax는 클래스의 차이만 있을 뿐 수학적으로는 같은 함수이다. (이 부분의 증명은 아래의 그림에 나와있고, 자세한 설명은 logit, sigmoid, softmax의 관계 참고할 것)
  • sigmoid: softmax에서 K=2일 때, 이진 분류에 사용
  • softmax: sigmoid 함수를 K개의 클래스로 일반화, 다중 분류에 사용

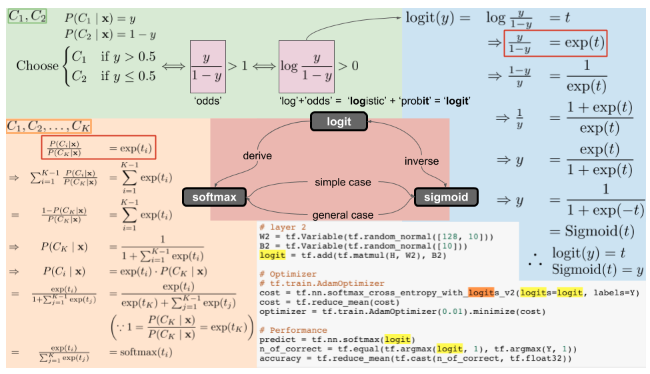
[logit, sigmoid, softmax의 관계, 출처: https://opentutorials.org/module/3653/22995]

• logit은 여러 블로그를 찾아보았지만 그 설명이 불명확하다. 영문 자료를 찾아봐야할 것 같다.

참고

• 로짓(Logit) 이란?
• logit, sigmoid, softmax의 관계
• Sigmoid, Logit and Softmax
• https://hwiyong.tistory.com/335
• https://junklee.tistory.com/97