고유값과 고유벡터

• 머신러닝 - 19. 고유값(eigenvalue), 고유벡터(eigenvector), 고유값 분해(eigen decomposition)를 정리한 내용

고유값(eigenvalue)과 고유 벡터(eigenvector)

정방행렬 A를 선형 변환으로 봤을 때, 선형변환 A에 의한 변환 결과가 자기 자신의 상수배가 되는 0이 아닌 벡터를 고유 벡터, 상수배 값을 고유값이라고 한다.

$Av= \lambda v$

위의 식의 해석은 벡터 v에 대해 선형 변환 A를 해주었을 때 벡터 v의 방향은 변하지 않고 크기만 변했다는 뜻이다.

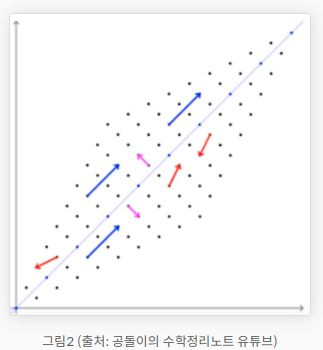
그림 2는 그림 1을 선형 변환한 것이고, 여기서 파란색 벡터와 분홍색 벡터가 고유벡터이다. 파란색 벡터는 고유값만큼의 비율로 크기가 변했고, 분홍색 벡터의 고유값은 1이다.

고유값 계산

고유값 정의에 의해 $(A-\lambda I)v=0$이므로 $(A-\lambda I)$의 역행렬이 존재하면 v=0이다. 그러나 정의에서 열벡터 v는 0이 아니므로 $(A-\lambda I)$는 역행렬이 존재하지 않는다. 즉 $det((A-\lambda I))=0$를 구하면 고유값과 고유벡터를 구할 수 있다. 열벡터 v는 수많은 해가 있을 수 있지만 고유벡터는 일반적으로 정규화된 벡터로 정한다.

고유값 분해(eigen decomposition)

행렬 A의 고유값을 ${\lambda}_i$, 고유벡터를 $v_i$(i=1,2,...,n)이라고 하자. 행렬 A의 고유벡터를 열벡터 로 하는 행렬을 P, 고유값을 대각원소로 가지는 대각 행렬을 B라고 하면 다음 식이 성립한다.

$A=PBP^{-1}$

이를 행렬 A에 대한 고유값 분해라고 한다. 행렬 A를 고유벡터와 고유값으로 분해한 것이다.
대칭행렬은 모두 고유값 분해가 가능하고, 직교행렬($AA^T=I$인 행렬 A)로 분해할 수 있다.