고유값과 고유벡터의 의미

고유값과 고유벡터

정의

n차 정사각형 행렬 을 A라고 할 때, $\mathbf 0$이 아닌 벡터 $\mathbf x \in R^n$가 적당한 스칼라 $\lambda$에 대해 아래의 식을 만족하면 $\lambda$를 A의 고유값(eigenvalue)라 하고, $\mathbf x$를 $\lambda$에 대응하는 A의 고유벡터(eigenvector)라고 한다.

$A\mathbf x = \lambda \mathbf x$

해석

• n차 정사각형 행렬: 선형 변환(좌표 공간 내에서 일어날 수 있는 모든 변환, 축소, 회전, 반사 등)
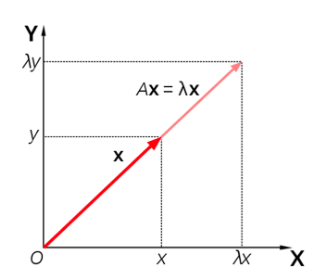
• $A\mathbf x$: 벡터 $\mathbf x$에 선형변환(A)를 취한 것
• 고유 벡터: 방향(direction)은 변하지 않고 크기(magnitude)만 변한 벡터
• 고유값: 고유 벡터가 변한 크기, 예를 들어 고유값이 2라면 기존 벡터가 2배만큼 길어진 것이다.

고유값은 최대로 서로 다른 n개의 고유값이 존재한다. (참고: 복소평면에서는 n개의 고유값이 존재한다.)

선형변환은 대개 고유벡터와 그에 대응하는 고유값으로 완전히 설명할 수 있다. (위키백과)

고유공간

$\lambda$가 n차의 정사각행렬 A의 고유값일 때 동차연립방정식 $(\lambda I_n -A)\mathbf x = \mathbf 0$의 해공간을 $\lambda$에 대응하는 A의 고유공간(eigenspace)라고 한다.

즉 $\lambda$에 대응하는 A의 고유공간은 $\lambda$에 대응하는 A의 고유벡터 전체와 영벡터로 이루어진 집합이고 이는 벡터공간 $R^n$의 부분공간이다.

고유 공간은 행렬 A의 고유벡터들이 기저를 이루어 생성하는 공간이다.

고유값과 고유벡터의 기하학적 의미

선형 연산자의 행렬이 있을 때 이 행렬이 벡터에 가하는 변환을 고유 공간에서의 변환으로 해석하면, 이 변환을 확대/축소 변환만으로 이해할 수 있다. 이는 원래의 직교기저가 생성하는 벡터 공간에서의 변환(회전, 확대, 축소)을 이해하는 것보다 훨씬 쉽다. 따라서 고유값과 고유 벡터는 다양한 분야에서 응용되는 경우가 많다.

• 정의 참고: 선형대수학(저자: 이상구, 이재화, 김경원)
• 참고
  https://losskatsu.github.io/linear-algebra/eigen/#
  https://angeloyeo.github.io/2019/07/17/eigen_vector.html