[밑시딥 2권] 2.4 통계 기반 기법 개선하기

2.3에서는 단어의 동시발생 행렬을 만들어 단어를 벡터로 표현하였다. 그러나 동시발생 행렬에는 개선할 점이 있다.

2.4 통계 기반 기법 개선하기

2.4.1 상호정보량

동시발생 행렬의 원소는 두 단어가 발생한 횟수를 나타내지만 고빈도 단어 측면에서 보면 좋은 특징이 아니다. 예를 들어 "the-car"보다 "car-drive"의 관련성이 더 높지만 동시발생 행렬을 이용하면 "the-car"의 연관성이 더 높다고 나올 것이다. 이 문제를 해결하기 위해 점별 상호정보량(Pointwise Mutual Information, PMI)라는 척도를 사용한다. PMI의 값이 높을수록 두 단어가 관련성이 높다.

• PMI의 식: $PMI(x, y) = log_2 \frac {P(x,y)}{P(x)P(y)}$

($P(x)$: $x$가 일어날 확률, $P(y)$: $y$가 일어날 확률, $P(x, y)$: $x, y$가 동시에 일어날 확률)

위의 식을 동시발생 행렬(각 원소는 동시발생한 단어의 횟수)을 사용하여 다시 써보면 아래와 같다.

$PMI(x, y) = log_2 \frac {P(x,y)}{P(x)P(y)} = log_2 \frac {\frac {C(x,y)}{N}}{\frac {C(x)}{N} \frac {C(y)}{N}} = log_2 \frac { {C(x,y)}{N}}{C(x)C(y)}$

($C$: 동시발생 행렬, $C(x, y)$: 단어 $x, y$가 동시발생하는 횟수, $C(x)$, $C(y)$: 각 단어 $x, y$의 등장 횟수, N: 말뭉치에 포함된 단어 수)

• 말뭉치 단어의 수 N: 10,000
  $C("the")=1000, C("car")=20, C("drive")=10$
  $C("the","car")=10, C("car", "drive")=5$
• 동시발생 횟수관점: "car"는 "drive"보다 "the"와 관련이 깊다.
• PMI 관점: "car"는 "the"보다 "drive"와의 관련성이 깊다.
  $PMI("the", "car") = log_2 \frac {10\cdot 10000}{1000 \cdot 20} \approx 2.32$
  $PMI("car", "drive") = log_2 \frac {5\cdot 10000}{20 \cdot 10} \approx 7.97$

위와 같이 원하는 결과가 나온 이유는 단어의 단독 출현 횟수가 고려되었기 때문이다. 그러나 위의 식에도 문제가 있는데, 두 단어의 동시발생 횟수가 0이면 $log_2 0 = -\infty$가 된다는 것이다. 이 문제를 해결하기 위해서 양의 상호정보량(Positive PMI, PPMI)를 사용한다. PPMI를 사용하면 단어 사이의 관련성을 0 이상의 실수로 나타낼 수 있다. 식은 아래와 같다.

$PPMI(x, y) = max(0, PMI(x, y))$

아래의 그림은 동시발생 행렬과 동시발생 행렬을 변화시킨 PPMI행렬이다.

그러나 PPMI 행렬에는 말뭉치의 어휘 수가 증가함에 따라 각 단어 벡터의 차원수가 증가한다는 문제가 있다. 또한 행렬의 원소 대부분이 0이다. 이는 벡터의 원소 대부분의 '중요도'가 낮다는 뜻이고, 이런 벡터는 노이즈에 약하고 견고하지 못하다는 약점이 있다. 이 문제를 해결하고자 자주 수행하는 기법이 벡터의 '차원 감소'이다.

2.4.2 차원 감소

차원 감소는(Dimensionality reduction) "중요한 정보"는 최대한 유지하면서 벡터의 차원을 줄이는 방법이다.

• PCA
  아래의 그림은 데이터를 넓게 분포시키는 중요한 축을 찾아 차원 축소를 시킨 것이다. 데이터에 새로운 축을 도입할 때, 각 데이터점의 값은 새로운 축으로 사영된 값으로 변한다. 여기서 중요한 것은 가장 적합한 축을 찾는 것으로 1차원 값만으로도 데이터의 본질적인 차이를 구별할 수 있어야 한다.

SVD(특이값 분해)

차원 감소 방법 중 특이값 분해(Singular Value Decomposition, SVD)은 임의의 행렬을 세 행렬의 곱으로 분해하며 수식은 아래와 같다.

$X = USV^T$

($U, V$: 직교행렬(Orthogonal matrix), 그 열벡터는 서로 직교한다.
$S$: 대각행렬(diagonal matrix), 대각성분 외에 모두 0인 행렬)

직교행렬 $U$는 어떤 공간의 축(기저)을 형성하며, 여기서는 '단어공간'이다. 대각행렬 $S$의 대각성분에는 "특잇값(해당 축의 중요도)"이 큰 순서로 나열되어 있다.

특잇값이 작다면 중요도가 낮다는 뜻이므로 행렬 $S$에서 여분의 열벡터를 제거하여 원래의 행렬을 근사할 수 있다. '단어의 PPMI 행렬'에 적용하면 행렬 $X$의 각 행에는 해당 단어의 ID의 단어 벡터가 저장되어 있고, 그 단어 벡터가 행렬 $U'$라는 차원 감소된 벡터로 표현된다.

차원감소의 결과로 원래의 희소벡터는 '밀집벡터'로 변환된다. 이것이 단어의 분산 표현이다.

• 행렬의 크기가 N이면 SVD 계산은 $O(N^3)$이 걸린다. 계산이 감당하기 어려울 정도로 오래 걸리므로 Truncated SVD를 사용하였다.

• 직교행렬
  $QQ^T=Q^TQ=I$ ($Q$: 정사각행렬)
  $Q^T=Q^{-1}$인 성질이 있다.
  [참고: Orthogonal Matrix (직교 행렬) 이란?]

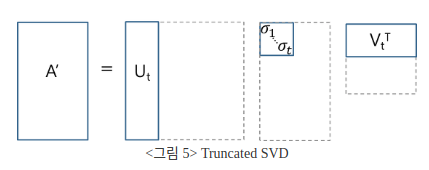
• Truncated SVD
  
  위의 그림은 Truncated SVD을 나타낸다. Σ에서 대각파트가 아닌 0으로 구성된 부분, 0인 singular value, 0이 아닌 singular value까지 제거한 형태로, U에서는 이에 대응되는 열벡터를 제거한다. 이 경우, 원래의 X는 보존되지 않고 X에 대한 근사행렬 X'이 나온다.
  (참고: [선형대수학 #4] 특이값 분해(Singular Value Decomposition, SVD)의 활용

2.4.3 SVD에 의한 차원 감소

SVD를 파이썬 코드로 실행하여 각 단어를 2차원 벡터로 표현한 후 그래프로 그리면 아래와 같다.

"goodbey"와 "hello", "you"와 "i"가 가까이 있음을 볼 수 있지만 사용한 말뭉치가 작아서 그 결과는 완전히 신뢰할 수 없다.

2.4.4 PTB 데이터셋

펜 트리뱅크(Penn Treebank, PTB)는 주어진 기법의 품질을 측정하는 벤치마크로 자주 이용되는 말뭉치이며, word2vec의 발명자인 토마스 미콜로프(Tomas Mikolov)의 웹페이지에서 받을 수 있다.

PTB 데이터셋에서 맥락에 속한 단어의 등장 횟수를 센 후 PPMI 행렬로 변환하고 SVD를 사용해 차원을 감소시킴으로써, 단어의 의미 혹은 문법적인 관점에서 비슷한 단어들이 가까운 벡터들로 나오는 좋은 단어 벡터를 얻을 수 있다. 이것이 단어의 분산 표현이다. 여기서 각 단어는 고정 길이의 밀집벡터로 표현되었다. 대규모의 말뭉치를 사용하면 단어의 분산 표현의 품질은 더 좋아질 것이다.

• 희소행렬/벡터: 원소 대부분이 0인 행렬 또는 벡터
• 밀집벡터: 원소 대부분이 0이 아닌 값으로 구성된 벡터 -> 단어의 분산표현