[풀잎스쿨] CS231n 3강 (2) Optimization & Image Features

• 스탠퍼드 대학의 CS231n: Convolutional Neural Networks for Visual Recognition
  본 포스팅은 CS231n 3강의 내용을 정리한 것이다. 이곳에 출처가 따로 언급되지 않은 이미지들은 스탠퍼드 대학에서 제공하는 강의 슬라이드에서 가지고 왔다.

[CS231n] http://cs231n.stanford.edu/2017/syllabus.html

Optimization

최적화(Optimization)는 큰 계곡을 걷는 것과 같다. 풍경은 파라미터 $W$, 산의 높이는 loss이다. $W$은 loss에 따라 달라진다. 그리고 우리의 목표인 최적화는 계곡 밑바닥에 닫는 것, 즉 가장 낮은 loss를 찾는 것이다.

Random Search

최적화를 찾는 가장 단순한 방법에는 Random Search 가 있다. 샘플링한 (임의의) $W$를 계산하여 나온 모든 loss를 비교하여 가장 작은 loss를 찾는 방식이다.

그러나 이 방식은 추천하지 않는다. CIFAR-10에서 Random Search 방식을 썼을 때, 15.5%의 정확도만 나왔기 때문이다. 최신 알고리즘인 SOTA에서는 95%의 정확도를 보였다(2017년 기준).

Follw the slope

Random Search보다 더 나은 방식이며, 기하학적 정의를 이용한 것이 Follw the slope(Gradient Descent, 경사하강법) 이다. 두 발로 땅의 경사를 느낀 후, 어느 방향으로 갈지를 정하는 것을 반복하는 방식이다. 단순해서 잘 동작하며 NN, Linear Classifier 학습에 많이 사용된다. 이 방식은 편미분(partial derivatives) 값을 갖는 벡터인 기울기(Gradient)를 사용한다.

Numerical gradient

위의 그림은 유한차분법을 이용하여 gradient dW를 구하는 Numerical gradient 법을 보여준다. W에 작은 h를 더해 loss를 계산하여 식과 같이 gradient dW를 구한다. 예를 들면, W=0.34, h=0.0001일 때 loss는 1.25322이고, 이를 이용하여 구한 gradient dW는 -2.5이다.

2번째에서도 위와 같은 방식으로 gradient dW를 구한다. 이런 방식으로 모든 차원에서 반복하여 기울기를 구할 수 있다.

그러나 Numerical gradient는 시간이 오래 걸린다. CNN과 같이 큰 함수라면 수천 개의 함수를 구해야 하고, 따라서 함수를 구하는 시간은 오래 걸린다. 그러므로 이 방식은 사용하지 않는 것이 좋다. 식 하나로 계산 가능한 Analytic gradient 를 계산하는 것이 효율적이고 더 정확하다.

Analytic gradient

Analytic gradient에서 함수와 가중치 W만 있으면 기울기 gradient dW를 바로 구할 수 있다. Loss function을 W에 의해 미분함으로 그 값이 나온다. Gradient가 증가하는 방향의 반대 방향(즉 감소하는 방향, 우리는 Loss의 최소값을 찾기 때문)으로 움직이며 Loss의 최소값을 찾으면 된다.

정리하면 Numerical gradient는 계산이 쉽지만 계산 시간이 오래 걸리고 근접한 값만 얻을 수 있다. 반대로 Analytic gradient는 계산이 정확하고 빠르지만 에러가 발생하기 쉽다.

실제로 사용할 때는 항상 Analytic gradient를 사용하고, 미분코드가 잘 작동하는지 확인하기 위해 Numerical gradient를 디버깅 툴로 사용한다. 이를 gradient check 이라고 한다. 참고로 Numerical gradient를 사용할 때는 파라미터의 스케일을 줄여 시간을 단축해야 한다.

Gradient Descent를 통해 최적화를 할 수 있다. 위의 알고리즘에 대한 설명은 다음과 같다. W를 임의의 값으로 초기화하고 True일 때, 기울기를 계산한다. 여기서 기울기는 증가하므로, -를 붙여 기울기가 감소하도록 한다. 음수인 기울기를 조금씩 이동해서 최종 결과를 얻는다.

(여기서 step size(=learning rate)에 따라 최적화에 도달하는 속도가 달라진다. (엄밀히 말하면 step size와 learning rate는 다르다. step size는 어느 정도의 크기로 이동할 것인가를 보여주고 learning rate는 어느 정도의 비율로 이동할 것인가를 보여준다.) step size를 어떻게 주느냐에 따라 학습 속도가 달라지므로 가장 중요한 Hyperparameter이다. 그래서 Hyperparameter를 정할 때, 가장 먼저 확인한다고 강사는 말한다.)

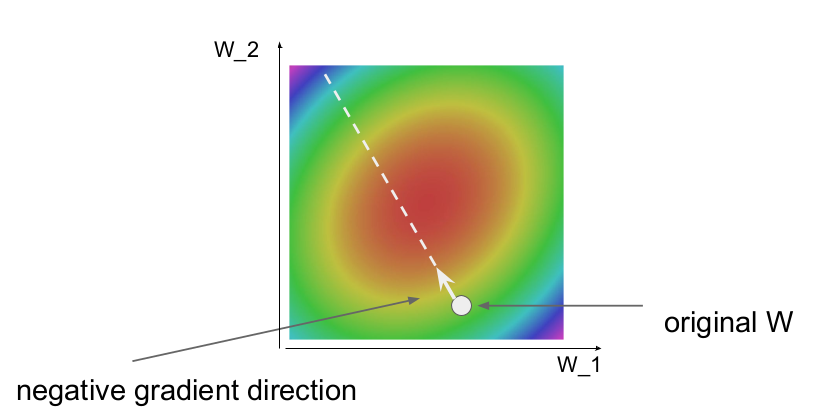
2차원 공간에서 손실함수를 그릇 모양이라고 하자. 빨간 부분은 낮은 loss를 가지고 있고, 파란 부분으로 갈수록 높은 loss를 가진다. 최적화를 위해서는 W가 빨간 부분으로 가야 한다. W가 초록 부분에 있다면 가장 낮은 지점(빨간 부분)에 도달할 때까지 gradient 계산을 반복 계산한다. 즉 매 step마다 W는 조금씩 $-gradient$ 방향으로 이동하는 식으로 W를 업데이트된다. 이를 update rule 이라고 한다.

이 다음 슬라이드(강의에 있음)에서는 더 좋은 성능을 내는 좋은 방법을 보여준다. 동영상을 통해 어떤 방법이 빨간 부분에 가장 빨리 도달하는가를 보여주었다. 보통 adam이 가장 빨리 도착하기 때문에 최적화에서는 adam을 사용하고 loss를 구할 때는 softmax를 주로 사용한다.

Gradient Descent를 계산할 때, 데이터의 수 N이 클수록 시간이 오래 걸린다. 데이터가 수백만 개라면 gradient를 수백만 번 계산해야 한다. SGD(Stochastic Gradient Descent)는 이를 보완하기 위해 나온 것으로, 데이터의 일부분(minibatch)에 대한 gradient를 구하고 이를 통해 실제 loss와 gradient를 추정하여 W를 update하는 방식이다. (minibatch의 수는 $2^n$로 하며, GPU의 메모리에 맞게 결정하면 된다.) 참고로 SGD는 DNN 알고리즘에서 많이 사용한다.

아래의 링크로 들어가 실습해 보자.
http://vision.stanford.edu/teaching/cs231n-demos/linear-classify/

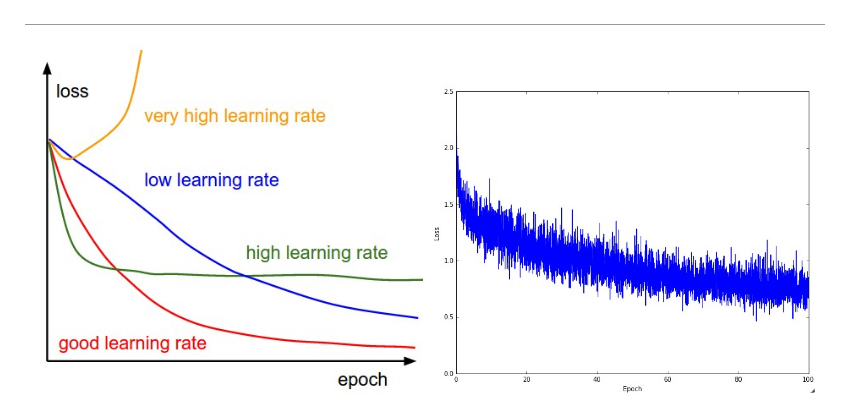
위의 그래프는 learning rate가 얼마나 중요한지 보여준다. learning rate가 너무 크면 Loss가 발산하고, 작으면 Loss가 너무 천천히 감소한다. learning rate가 크면 Loss가 local mininum에서 멈추게 된다. 따라서 좋은 learning rate를 선택하는 것이 중요하다.

Image Features

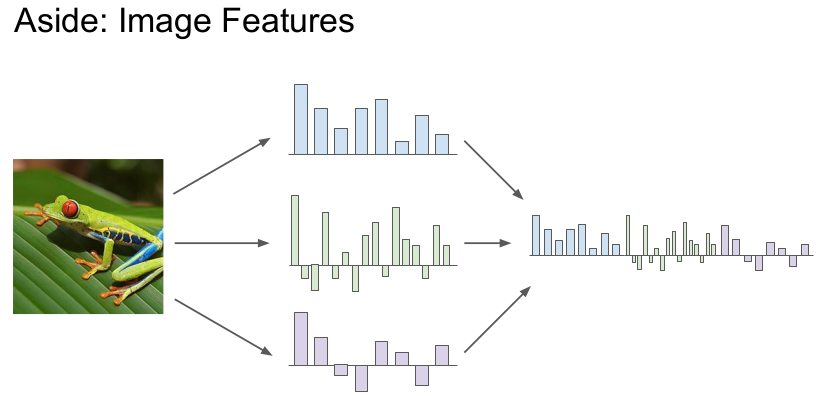
이미지를 분류하기 위해서는 이미지의 특징(features)를 추출해야 한다. 정제되지 않은 이미지 픽셀을 입력값으로 받아 이미지의 특징을 RGB로 추출하는 것을 보여준다. 그러나 이 방식은 좋지 않다.

왼쪽 그림은 linear classifier로 결정경계를 구할 수 없기 때문에 특징변환(feature transform)을 하여 점들을 선형 벡터로 바꾸어(오른쪽 그림) 선형함수로 분리할 수 있게 만들었다. 우리의 관심은 어떤 방식으로 특징변환을 할 것인가이다. (예: 극좌표계 변환 등) 이미지 특징 추출에는 3가지 유형이 있다.

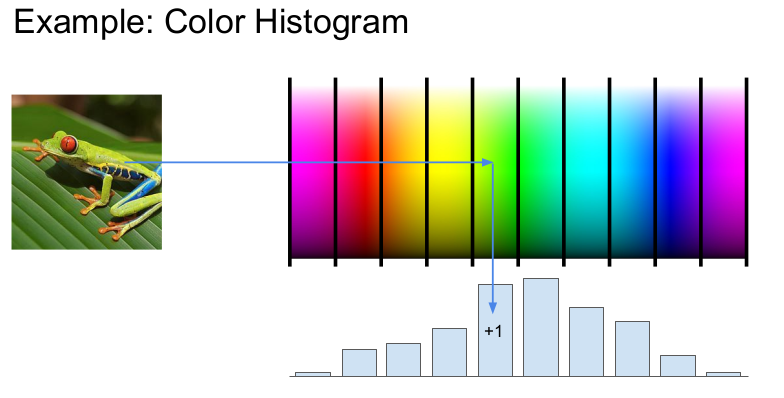
특징변환의 한 예는 Color Histogram 이다. 특정 색에 해당하는 픽셀의 수를 세어 히스토그램으로 표현하였다.

두 번째 방법은 Histogram of Oriented Gradient(HoG) 이다. 이미지를 $8\times 8$ 픽셀로 나누어 그 픽셀 지역 내 가장 지배적인 edge를 찾는다. edge를 양자화 시켜 edge orientation 히스토그램으로 표현한다. 이 방식은 예전에 영상 인식에서 많이 사용되었다.

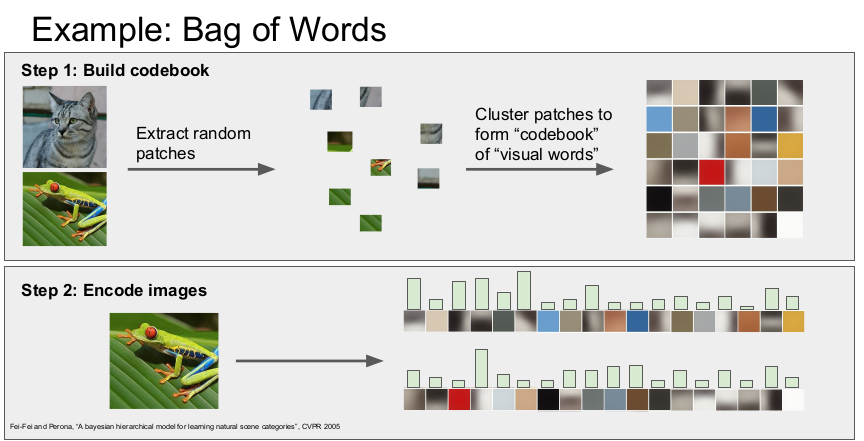
다음은 Bag of Words 이다. NLP(자연어처리)에서 영감을 받아 만들어진 방법으로, 2 단계로 수행된다. 1단계는 이미지를 작게 잘라 시각 단어로 표현한 후, "codebook"에 붙인다. K-means 알고리즘으로 1천개의 중심점을 갖도록 학습을 한다(색에 따라 군집화). 2단계는 이미지의 시각 단어의 발생 빈도를 인코딩하여 이미지의 특징을 추출한다.

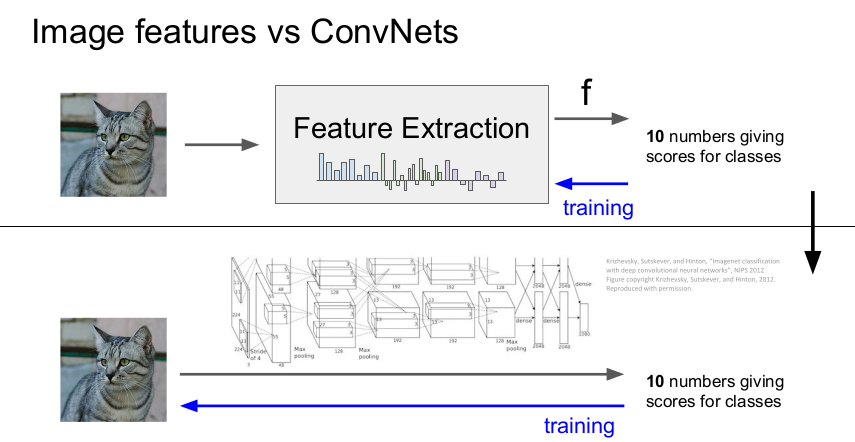
2012년 이전까지는 이미지 특징 추출(Feature Extraction)이 중요했다. 이미지의 특징을 추출하여 linear classifier의 입력으로 사용하고 학습하여 클래스의 점수를 알려주어 이미지를 분류하였다. 여기서 이미지의 특징은 학습시에는 변하지 않는다.

그러나 2012년 AlexNet이 나온 후, layer를 쌓으면서 데이터로부터 특징을 직접 추출하여 학습하는 방식(CNN이나 DNN)으로 변하였다. 즉 Linear classifier와 가중치를 한 번에 학습하는 식으로 변하였고, 얼마나 훌륭한 성능을 갖는 구조를 만드느냐가 중요해졌다.