• 스탠퍼드 대학의 CS231n: Convolutional Neural Networks for Visual Recognition
  본 포스팅은 CS231n의 내용을 정리한 것이다. 이곳에 출처가 따로 언급되지 않은 이미지들은 스탠퍼드 대학에서 제공하는 강의 슬라이드에서 가지고 왔다.
  [CS231n] http://cs231n.stanford.edu/2017/syllabus.html

이전 시간에 배운 최적화(Optimization)에서 가장 작은 loss를 구하기 위해서는 Analytic Gradient 방식으로 gradient와 loss를 구하는 것이 좋다라고 하였다. 이번 시간에는 gradient를 구하는 방법을 공부할 것이다.

Backpropagation(역전파)

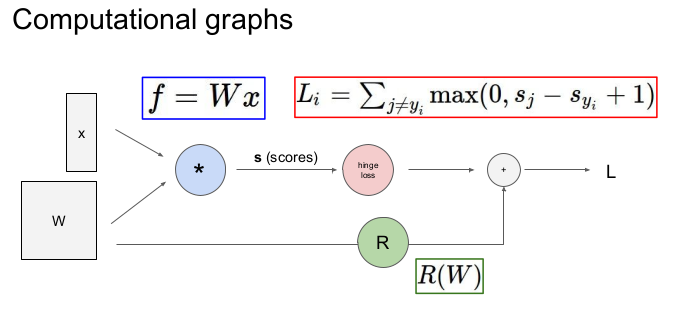
위의 그림은 Computational graphs 라고 부른다. 총 Loss를 구하는 것을 Computational graph를 통해 나타냈다(x와 W의 곱으로 만들어진 f함수를 통해 s(scores)를 구하고, s로부터 나온 hinge loss와 W로부터 나온 R(regularization term)을 더해 총 Loss를 구한다). 우리는 이와 같은 computational graph를 이용하여 gradient를 구할 것이다.

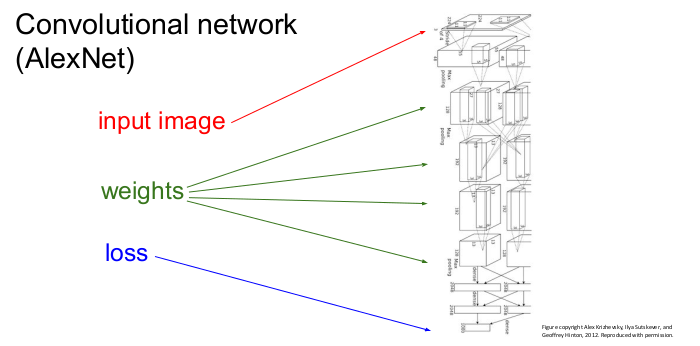
Convolutional network를 그림으로 표현한 것으로 입력 이미지가 위에서 들어가고 가중치를 통해 손실이 맨 밑으로 나옴을 보여준다.

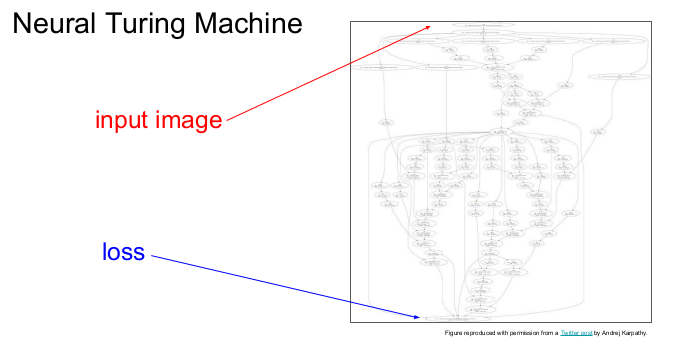
다음은 Neural Turing Machine을 그림으로 표현한 것으로, Convolutional network와 같이 입력 이미지가 위에서 들어가면 crazy한 함수들에 의해 loss가 밑으로 나오게 된다. Neural Turing Machine은 이런 과정이 여러 번 반복된다.

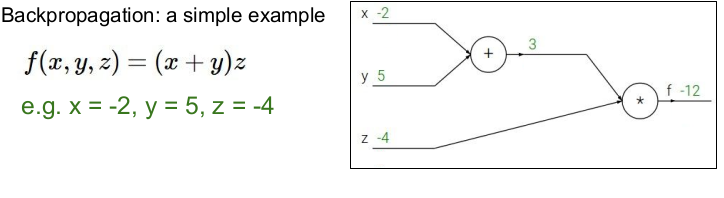
위의 그림은 Backpropagation(역전파)의 간단한 예를 나타낸 것이다. 역전파는 chain rule을 재귀적으로 사용하여 복잡한 함수 $f$의 gradient를 구한다.

역전파를 구하기 전에 먼저 각 변수에 값을 넣고 각 노드들의 값을 구해 그래프에 적어 넣는다. 여기서는 $x=-2, y=5, z=-4$를 넣어 $q=x+y=3$, $f=qz=-12$를 구하였다.

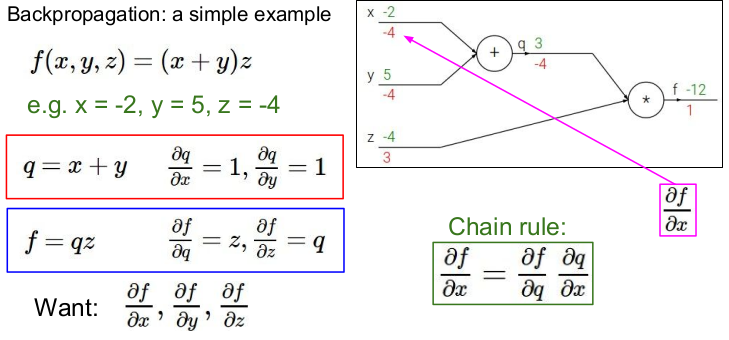
이제 우리는 $f$에서 거꾸로 거슬러 가 각 노드의 기울기를 구해야 한다.

1. 우선 s의 노드의 식을 $q=x+y$라고 하자. 그러면 $f=qz$가 된다. 두 식의 편미분을 우선 구해보자
   1) $q=x+y$의 편미분: $\frac{\partial q}{\partial x}=1$, $\frac{\partial q}{\partial y}=1$
   2) $f=qz$의 편미분: $\frac{\partial f}{\partial q}=z$, $\frac{\partial f}{\partial z}=q$

2. 각 노드의 기울기를 구한다.
   1) f에서의 기울기(편미분): $\frac{\partial f}{\partial f}=1$
   2) z에서의 기울기(편미분): $\frac{\partial f}{\partial z}=q=3$
   3) q에서의 기울기(편미분): $\frac{\partial f}{\partial q}=z=-4$
   4) y에서의 기울기(편미분): $\frac{\partial f}{\partial y}={\frac{\partial f}{\partial q}}{\frac{\partial q}{\partial y}}=z\times1=-4$
   5) x에서의 기울기(편미분): $\frac{\partial f}{\partial x}={\frac{\partial f}{\partial q}}{\frac{\partial q}{\partial x}}=z\times1=-4$

• Chain rule: $\frac{\partial f}{\partial x}={\frac{\partial f}{\partial q}}{\frac{\partial q}{\partial x}}$ (x와 y에서의 기울기를 구하기 위해서 chain rule을 사용하였다.)
  $\frac{\partial f}{\partial x}={\frac{\partial f}{\partial q}}{\frac{\partial q}{\partial x}}$ 는 합성함수 $f(x,y,z)$에서 다른 변수들을 상수 취급하고 편미분을 한 값을 의미한다. 편미분의 합은 전미분이 된다. 즉 각 방향에 대한 변화율의 합은 전체 변화율이 된다.

• $\frac{\partial f}{\partial q}$: $f$에 대한 $q$의 영향력을 말한다.

• 위의 그림에서 $\frac{\partial f}{\partial x}=-4$의 의미는 $x$가 변하면 $f$의 값은 -4만큼 변한다는 뜻이다. (x가 -2에서 -1로 1만큼 증가하면 f는 -12에서 -16으로 -4만큼 증가한다.)
  
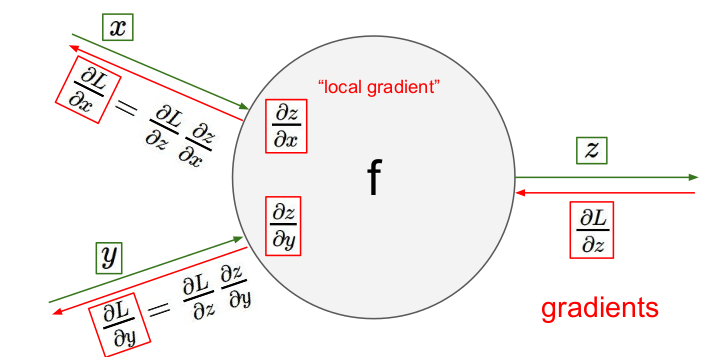
  "local gradient"는 들어오는 입력(z)에 대한 출력(x, y)의 기울기($\frac{\partial z}{\partial x}, \frac{\partial z}{\partial y}$)를 의미하며, 각 게이트에 local gradient가 존재한다. 함수의 graidents를 구하는 것은 어려우므로 계산 노드를 나누어 각 게이트에 대한 local gradient(쉬운 계산)를 구하고 각 게이트들의 local gradient를 합하여 전체 gradients를 구할 수 있다.

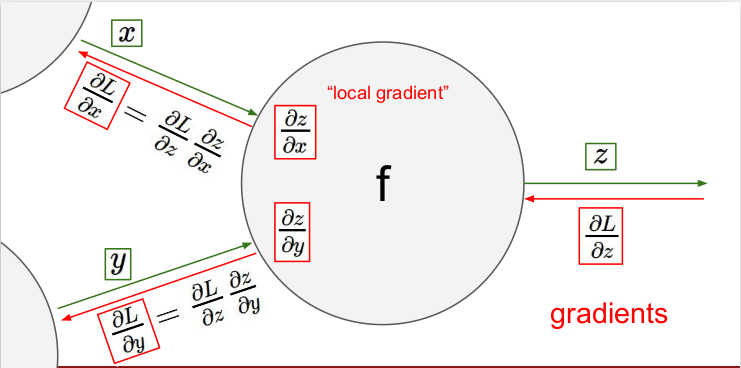
각 게이트마다 local gradient를 입력받고 다음 게이트로 출력값을 보낸다. 이 과정을 각 게이트마다 반복하는 것이므로 어렵지 않다. Backpropagation을 사용하여 출력값을 통해 입력값을 구할 수 있다.

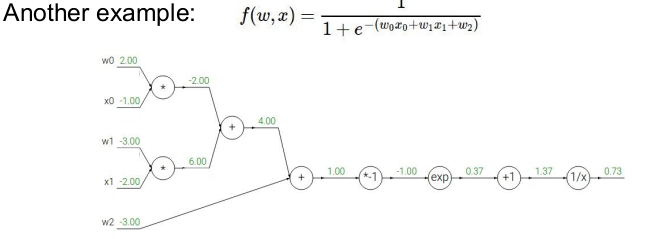
$f(w,x)=\frac{1}{1+e^{-(w_0x_0+w_1x_1+w_2)}}$의 Backpropagation은 다음과 같다.

1. 제일 먼저 각 노드(게이트)의 값을 계산해둔다.

2. 필요한 함수의 미분 값을 계산해둔다.
   1) $f(x)=ax$ 의 미분: $\frac{\mathrm {d} f}{\mathrm {d} x}=a$
   2) $f(x)=e^x$ 의 미분: $\frac{\mathrm {d} f}{\mathrm {d} x}=e^x$
   3) $f(x)=c+x$ 의 미분: $\frac{\mathrm {d} f}{\mathrm {d} x}=1$
   4) $f(x)=\frac {1} {x}$ 의 미분: $\frac{\mathrm {d} f}{\mathrm {d} x}=-\frac {1}{x^2}$

3. 각 노드(게이트)의 기울기를 구한다.
   1) $\frac{\partial f}{\partial f}=1$
   2) $\frac{1}{x}$ 의 기울기: $1*-\frac {1}{1.37^2}=-0.53$
   3) $+1$ 의 기울기: $(-0.53)*1=-0.53$
   4) $exp$ 의 기울기: $(-0.53)*e^{-1}=-0.20$
   5) $*-1$ 의 기울기: $(-0.20)*(-1)=0.20$
   6) $+$ 의 기울기: $(0.20)*1=0.20$
   7) $*$ 의 기울기: (-0.20)*(반대편 값)
   

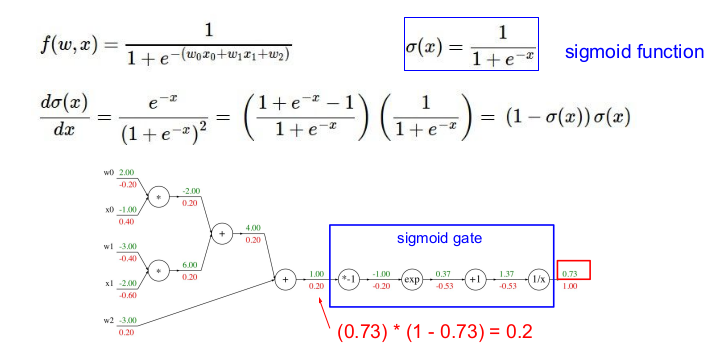
역전파를 구했던 함수는 sigmoid 함수와 비슷하게 생겼다. sigmoid 함수는 미분하면 자신을 포함한 식이 되기 때문에(sigmoid 함수의 독특한 특성임) 우리가 구했던 복잡했던 역전파 중 일부는 sigmoid gate와 같고, 이 게이트를 사용해 위와 같이 쉽게 구할 수 있다. 이를 modularity라고 부른다.

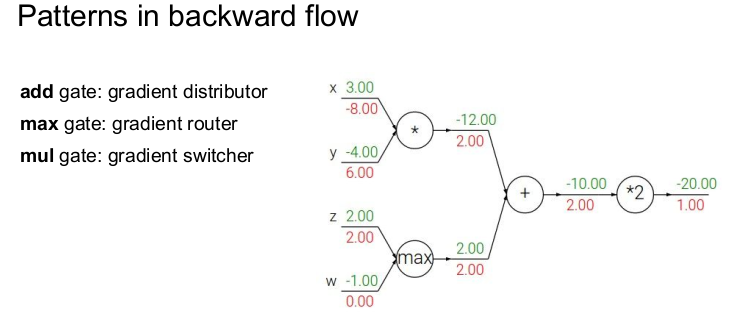
역전파에는 3가지 패턴이 존재한다. 우선 더하기 게이트(add gate)의 경우는 입력되는 기울기를 그대로 출력값으로 전파해주므로(local graident=1) gradient distributor라고 부른다. 최대값 게이트(max gate)는 z와 x 중 큰 값만 그의 local graident인 1을 전해주고 나머지는 0이 되기 때문에 gradient router라고 부른다. 이렇게 되는 이유는 forward할 때, 큰 값만 다음 식에 영향을 미치기 때문이다. 곱셈 게이트(mul gate)의 경우는 미분했을 경우, 반대편의 값이 나오기 때문에 반대편의 값을 들어오는 기울기와 곱해주면 된다. 따라서 곱셈 게이드를 gradient switcher/scaler라고 부른다. 이 패턴을 기억하면 역전파를 계산하기 편하다.

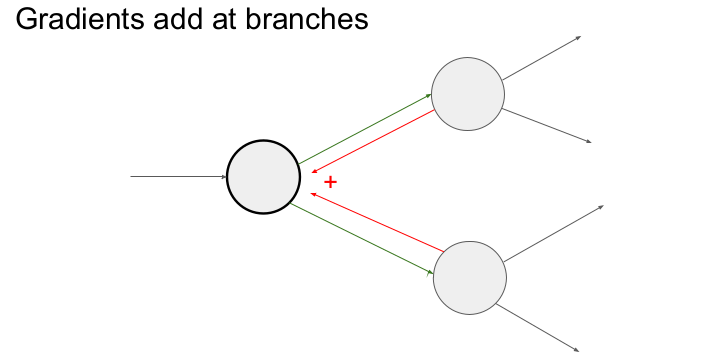
만약 입력되는 기울기가 2개 이상(다변수 chain rule)이라면 어떻게 할까? 입력되는 기울기 모두를 더하면 된다. 그 이유는 forward pass할 때, 입력값이 연결된 모든 게이트에 영향을 미치기 때문이다. $\frac {\partial f} {\partial x}=\sum {\frac {\partial f}{\partial q_i}}{\frac {\partial q_i}{\partial x}}$

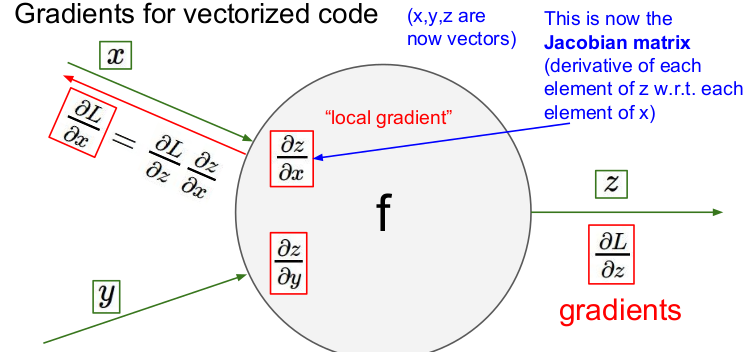
x, y, z가 모두 벡터인 경우의 기울기는 어떻게 구할까? local gradient는 각 요소의 미분을 포함한 행렬인 야고비 행렬(Jacobian matrix)라고 한다. 야코비 행렬의 각 행은 입력값에 대한 출력의 편미분으로 이루어져 있다.

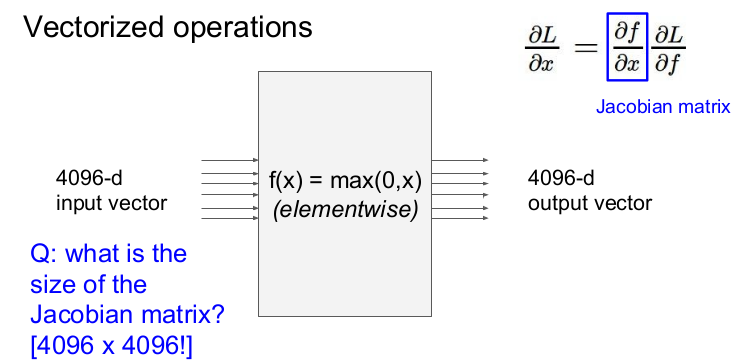
입력값과 출력값이 4096차원 벡터이면 야코비 행렬의 크기는 (4096x4096)이 된다.

실제로 우리는 전체가 아닌 minibach(배치가 100이라면)를 사용하므로 총 (409,600x409,600)의 행렬이 될 것이다. 이는 너무 큰 행렬이기 때문에 실용적이지 않고, 계산할 필요도 없다.

그렇다면 야코비 행렬은 어떻게 생겼을까? 야코비 행렬은 elementwise이므로 그 자리에 있는 것만 곱하고, 자기 자신만 영향을 받으므로 대각 행렬처럼 생겼을 것이다. 다만 대각행렬에서는 1만 존재했던 대각선이 0과 1이 섞여 있는 것(sparse structure)으로 나타날 것이다. 그러나 실제로는 계산할 필요는 없다.

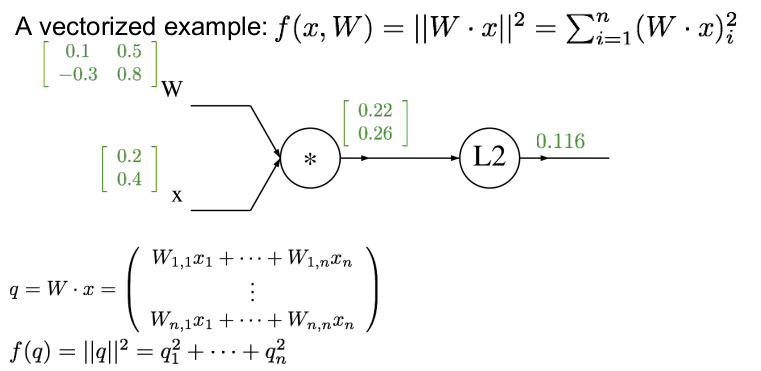
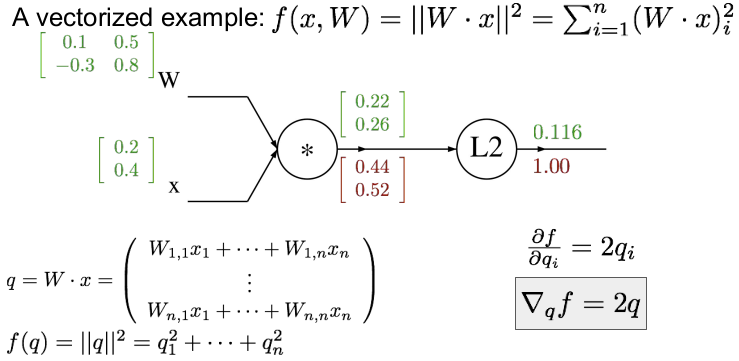
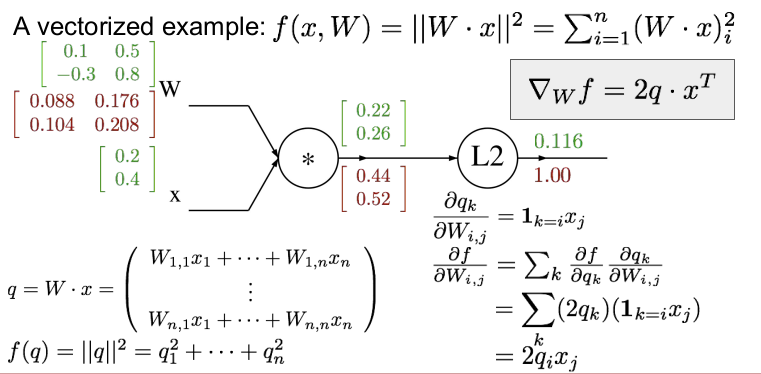
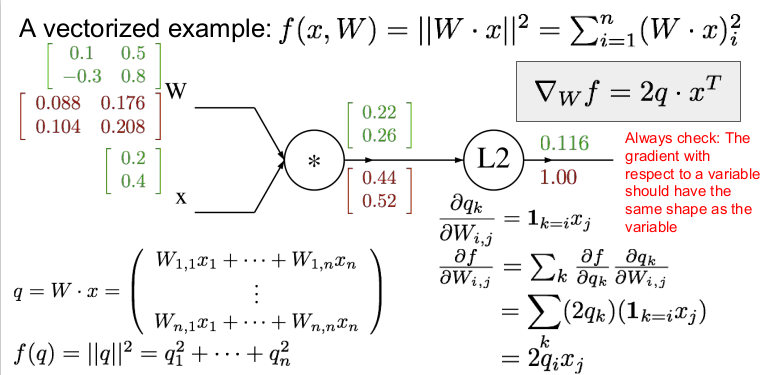
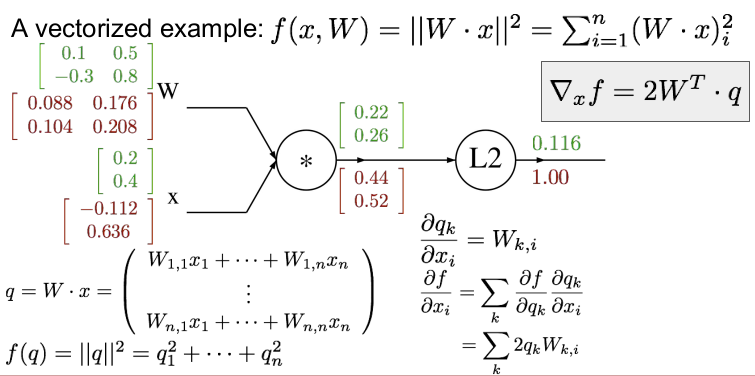
벡터화된 예를 들어보자. W와 x가 위와 같다면 먼저 forward pass를 하여 각각의 게이트의 값을 구하자. 각 게이트의 값은 행렬곱을 하면 쉽게 구할 수 있다. (행렬 미분에 대한 부분은 곧 공부하여 정리할 것이다.)

위의 그림은 forward/backward API를 사용하여 위에서 구했던 sigmoid 함수가 포함된 함수의 역전파를 코드로 구현한 것이다. 위에서는 forward를 구현하고, forward를 활용하여 backward를 구현하였다.


x, y, z가 스칼라일 때, 코드로 computational graph를 구현한 것이다. forward값을 저장하여 역전파할 때 사용하는 것을 볼 수 있다.

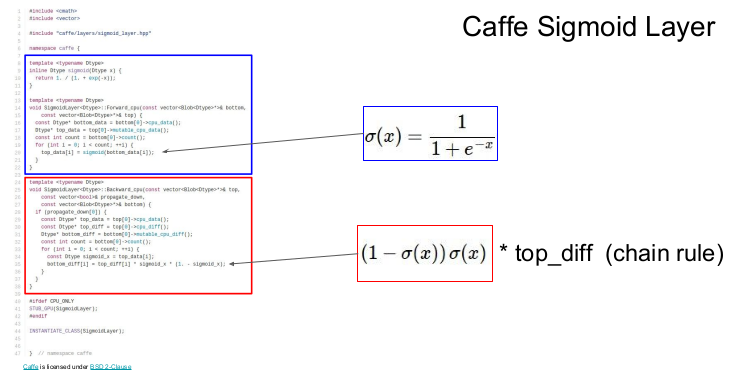
Caffe는 유명한 딥러닝 프레임워크인데, tensorflow가 나오면서 이제는 더이상 사용하지 않는다.

역전파는 computational graph를 chain rule을 재귀적으로 사용하여 모든 입력값의 기울기를 계산한다. backpropagation은 신경망의 핵심기술이며 forward pass할 때 나온 연산값을 저장하여 역전파에서 사용한다.