- 스탠퍼드 대학의 CS231n: Convolutional Neural Networks for Visual Recognition
본 포스팅은 CS231n의 내용을 정리한 것이다. 이곳에 출처가 따로 언급되지 않은 이미지들은 스탠퍼드 대학에서 제공하는 강의 슬라이드에서 가지고 왔다.
[CS231n] http://cs231n.stanford.edu/2017/syllabus.html
Convolutional Neural Networks

5강은 Convolutional Neural Networks을 다룬다. CNN은 선형인 층을 쌓고 비선형인 층을 쌓아 신경망을 만든다. 이를 통해 Mode 문제를 해결할 수 있다.
History of CNN

본격적으로 강의에 들어가기에 앞서 약간의 역사를 다루기로 한다. 1957년 최초로 perceptron을 구현되었고, 여기서 가중치 W를 업데이트하는 update rule가 나타났다.
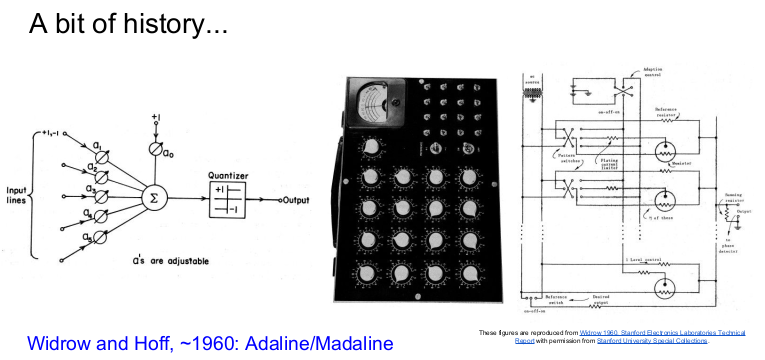
1960년에 Multilayer Perceptron Network인 Adaline/Madaline이 발명되었다.
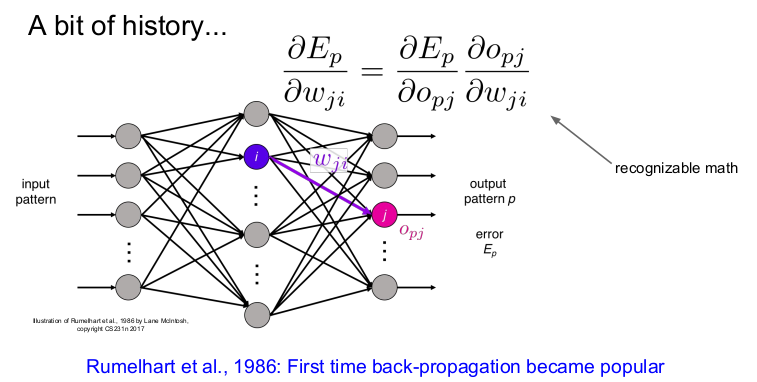
1986년 처음으로 backpropagation이 나타났고, 신경망의 학습이 시작되었다. 그러나 여러 가지 상황에 의해 다시 암흑기에 들어갔다.
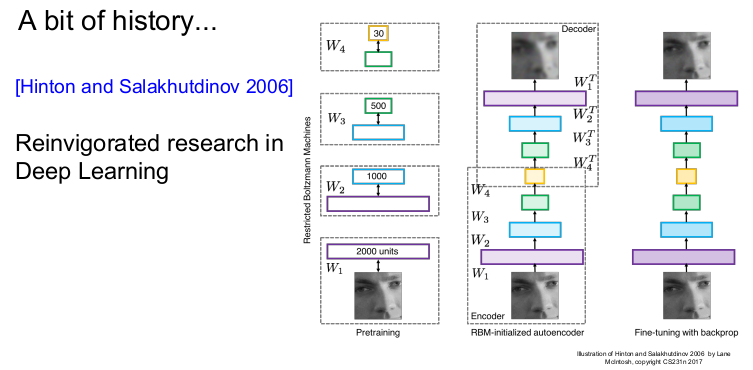
2006년 Deep Learning의 학습 가능성이 나타났다. 초기화에는 RBM이 이용되었고 hidden Layer에서 가중치가 학습되었다. 그 후 전체 신경망을 backpropagation을 하거나 fine-tuning하는 식으로 진행되었다.
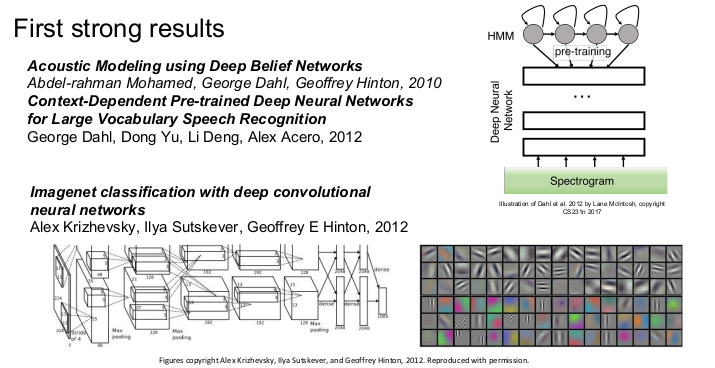
신경망의 광풍은 2012년부터 시작되었다. ImageNet 분류를 통해 에러를 극적으로 감소시키는 AlexNet가 landmark paper로 나타났다. 이 때부터 CNN이 널리 사용되기 시작했다.
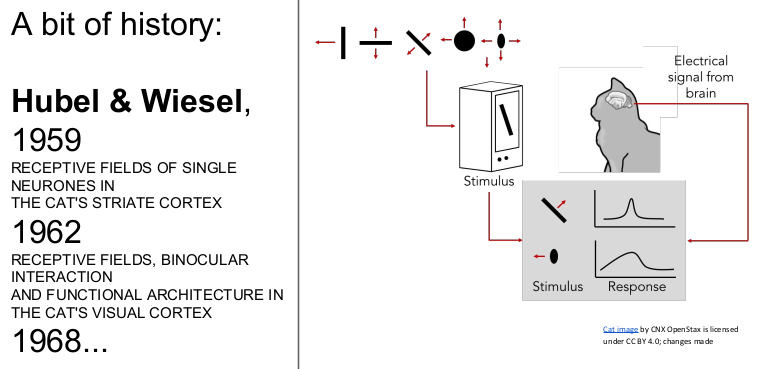
처음에는 고양이의 뇌에 신호로 자극을 주었을 때, 고양이가 edges와 shapes에 반응을 보인다는 것을 알게 되었다(고양이의 시각령 visual cortex 연구).

뇌의 특정 뉴런은 특정 방향에 반응한다는 것을 발견했다. (mapping, 지역성 보존)
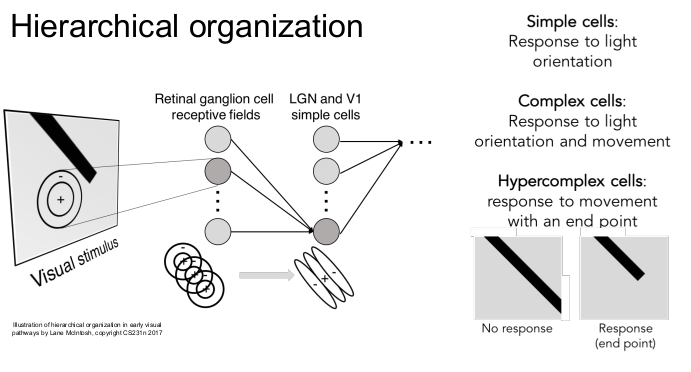
뉴런이 계층구조를 가진다는 것을 알아냈다. Retinal ganglion cell을 통해 시각정보를 받아들일 때, 빛의 방향에 반응을 보이는 simple cells로부터 빛과 움직임에 반응을 보이는 complex cells, 그리고 corner, blob 등 끝의 움직임을 보이는 hypercomplex cells의 계층 구조가 있다는 것을 발견하였다.
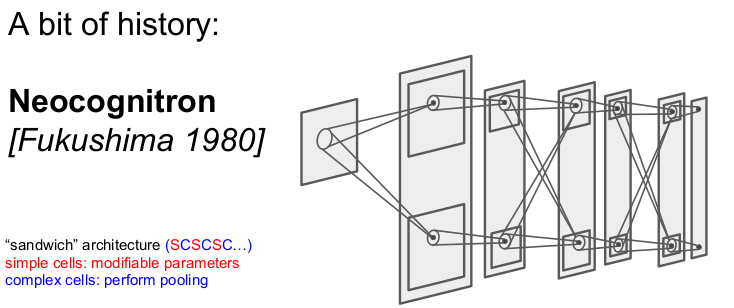
생물학적 성과를 컴퓨터로 simulation한 것이 Neocognitron이다. simple cell과 complex cell을 반복적으로 쌓아가는 '샌드위치' 구조를 가지고 있다. 그러나 backpropagation은 하지 못했다.
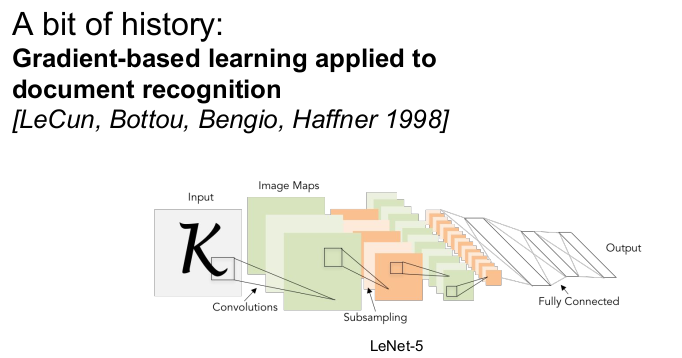
1998년 gradient-based learning이 글자 인식에 적용되었다. 이는 우편번호의 숫자를 인식하는 용도로 사용되었다. 이 모델은 backpropagation이 가능하다.

2012년, 신경망이 비약적으로 발전하여 CNN의 현대화된 모습인 AlexNet가 나타났다. 1998년에 나온 것과 구조는 다르지 않으나 더 크고 깊어진 것이 그 특징이다. 대규모의 데이터를 활용하였고 처음으로 GPU를 2대 사용하였다. 가중치 초기화를 잘 하였고 batch normalization을 하였다.
The Use of CNN

CNN은 다양한 분야에 사용된다. 이미지 분류, 이미지 검색(하나의 이미지를 주면 비슷한 이미지를 찾는다)에 사용된다.

Detection(실시간 detection을 하는 YOLO)과 각 픽셀에 라벨링을 하는 Segmentaion에도 사용된다.

Lidar를 통해 자율 주행에도 사용된다.
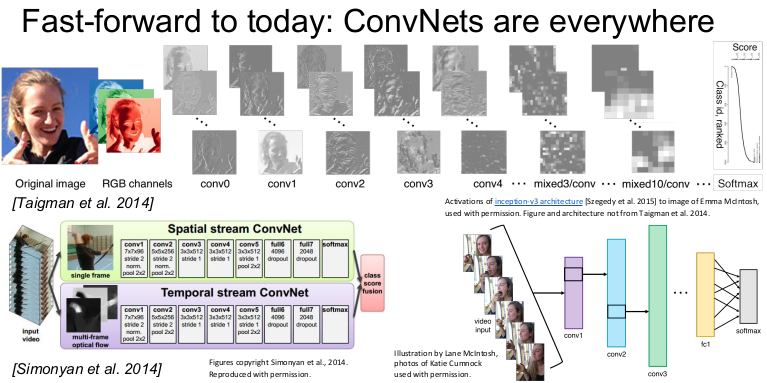
face recognition이나 비디오 인식(시간적 정보 활용)에도 사용된다.

pose recognition과 게임에도 사용된다.

의학 영상 해석과 진단에도 사용되며, 은하나 표지판 인식에도 사용된다.

캐클 챌린지에 나왔던 고래 분류와 항공지도를 통한 길과 건물을 인식하는 데에도 사용된다.

사진을 보고 이미지에 대한 설명을 하는 Image captioning에도 사용된다. Image captioning은 segmentaion을 하는 CNN과 text generation을 하는 RNN을 동시에 사용하여 할 수 있다. 글을 보고 이미지를 만들어 내는 Open AI의 Dall-E도 CNN을 사용하였다.

환각 속에서 그린 그림과 같은 그림(GAN 사용)을 그리거나 특정 화풍으로 그림을 그리는 style transfer에도 사용된다.
Convolutional Neural Networks

이제 CNN이 어떻게 동작하는지 알아보자.
Fully Connected Layer
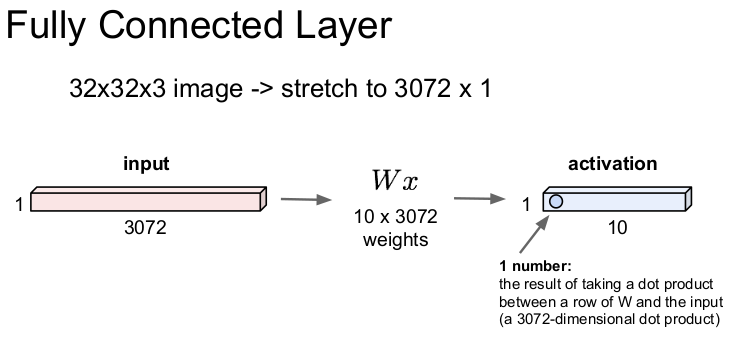
이전 강의에서는 Fully Connected Layer(FC layer/Dense Layer/Flatten Layer)에 대해 배웠다. FC Layer는 32x32x3의 이미지를 늘려서 3072x1의 벡터 x(1차원)로 만들어 가중치 W와 내적을 하여 1개의 숫자를 1x10의 activation layer에 출력한다.
Convolution Layer
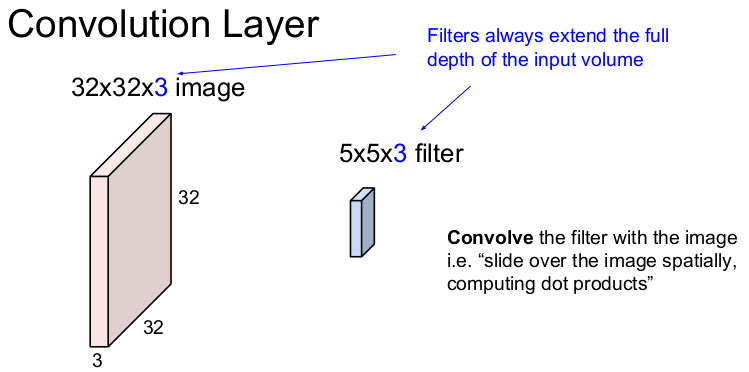
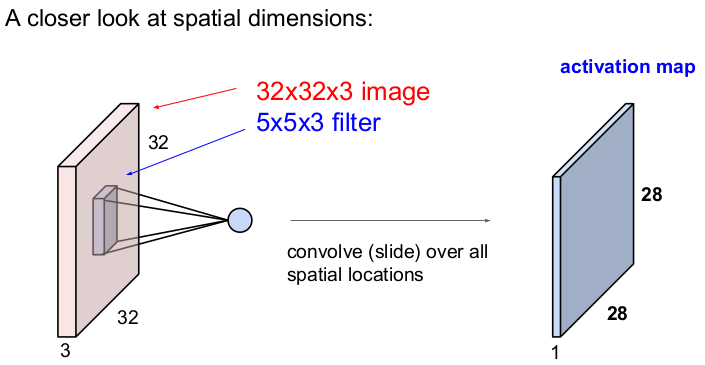
그러나 Convolution Layer는 기존의 이미지의 구조를 유지하고 filter와의 공간적 내적을 통해 1개의 숫자를 출력한다. 즉 32x32x3의 입력 이미지에 5x5의 filter를 움직이면서 하나의 값을 추출한다. (32x32x3의 입력 이미지에서 3은 RGB 3채널을 뜻하고 depth라고 부른다.) Convolution Layer에서는 filter의 크기를 정할 수 있다. filter의 가로와 세로의 크기는 5x5로 선택할 수 있지만 depth는 입력 이미지의 depth와 같아야 하므로 filter의 크기는 5x5x3이 된다. 입력 이미지에 filter를 슬라이딩하여 내적을 구하는 것을 convolve한다고 한다.
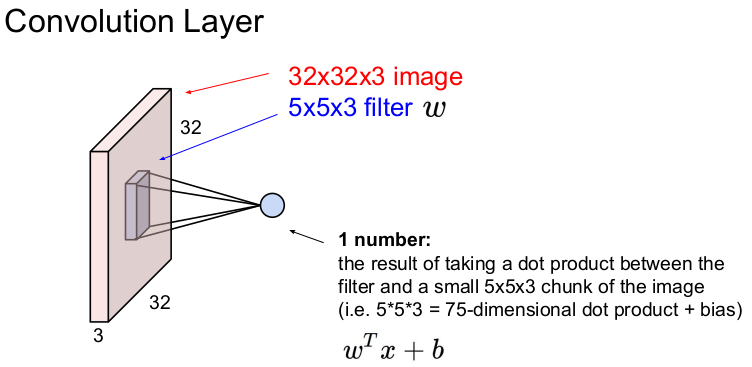
Convolution Layer에 filter를 convolve하면 1개의 숫자가 나온다. 즉 filter와 Convolution Layer의 일부(filter의 크기)를 내적하여 1개의 숫자가 나오게 된다. 만약 filter가 10번 슬라이딩(convolve)하면 10개의 숫자가 나온다. 1개의 숫자가 나오는 식은 이다. 여기서 는 5*5*3=75이고, b는 bias이다.
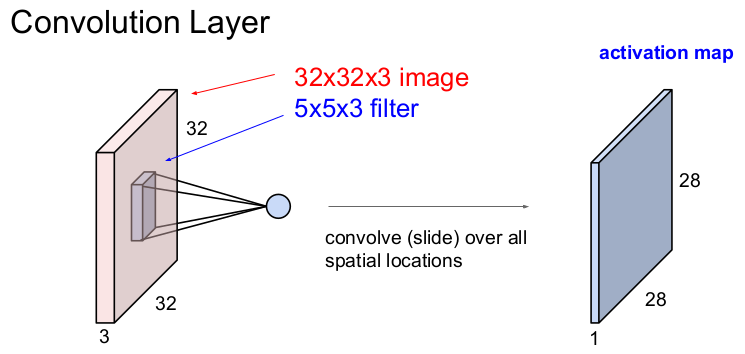
5x5x3의 필터가 32x32x3의 이미지를 좌측 상단에서 시작하여 우측 하단까지 1번 슬라이딩해가면서 내적하여 얻은 값을 모으면 28x28x1의 이미지를 얻게 되는데, 이를 activation map이라고 한다. 출력된 activation map의 크기는 filter의 크기와 숫자, 그리고 슬라이딩을 어떻게 하느냐에 따라 달라진다.
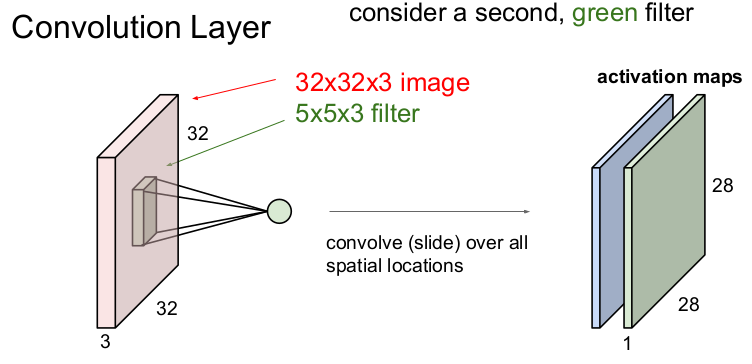
각 필터는 이미지로부터 1개의 특징을 추출하는데, CNN에서는 여러 개의 필터를 사용하므로 이미지로부터 여러 개(필터의 갯수)의 특징을 추출할 수 있다.
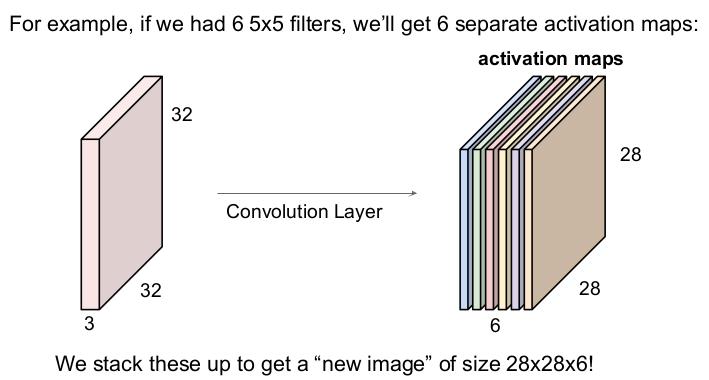
만약 6개의 5x5 크기의 필터를 사용한다면 입력 이미지와 필터가 6번 내적하므로 6개의 activation map을 얻을 수 있다. 그렇게 나온 6개의 activation map을 모아 크기 28x28x6의 "새 이미지"를 얻을 수 있다.
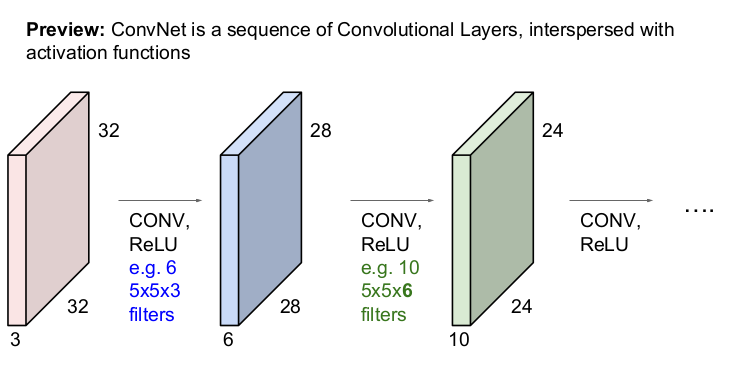
CNN에서는 입력 이미지가 convolution layer와 활성함수 ReLU를 통과하여 activation map을 얻고, 앞에서 얻은 activation map에 다시 convolution layer와 활성함수 ReLU를 통과하여 다시 activation map을 얻는 과정을 반복적으로 하게 된다. (ConvNet은 activation map이 흩어져 있는 Convolution Layers의 배열이다.)
그림을 설명하면 다음과 같다. 32x32x3의 입력 이미지를 6개의 5x5x3(입력 이미지의 depth가 3이므로 필터의 depth도 3)의 필터로 내적하여 28x28x6(필터의 개수가 6개이므로 depth가 6)의 activation map을 얻는다. 28x28x6의 activation map은 입력 이미지가 되어 10개의 5x5x6(입력 이미지의 depth가 6이므로 필터의 depth도 6)의 필터와 내적을 하고 24x24x10(필터의 개수가 10개이므로 depth가 10)의 activation map을 얻는다. 이 과정이 계속 반복된다.
CNN 모델 디자인은 필터의 크기와 숫자, 그리고 stride을 통해 다양하게 선택될 수 있다.
- 참고: CNN model에서 cnn.add(keras.layers.Conv1D(16,7, activation='relu')라고 써 있는 부분을 볼 수 있다. 여기서 16은 필터의 크기를 말한다.
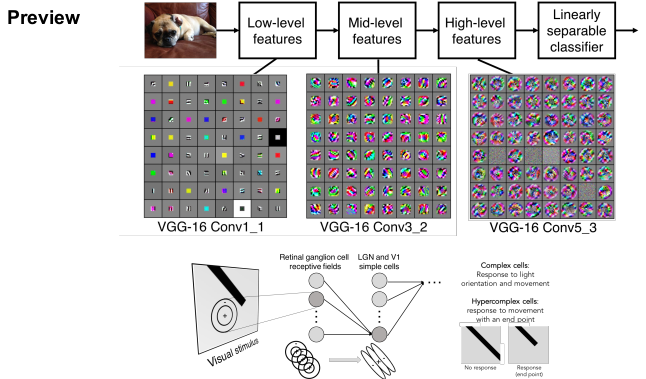
필터가 여러 개일 때, 필터는 이미지의 특징을 단순한 것부터 복잡한 것까지 계층적으로 학습하게 된다. 첫 번째 필터인 VGG-16 Conv_1에서는 Low-level features인 edges나 color를 학습한다. 두 번째 필터인 VGG-16 Conv3_2에서는 Mid-level features인 corner, blobs를 학습한다. 세 번째 필터인 VGG-16 Conv5_2에서는 High-level features(통합)를 학습한다. 즉 Convolutional layer가 깊어질수록(여러 개 쌓일수록) 이미지의 특징을 더 많이 추출하게 된다.
이는 CNN이 1959년 발견한 계층 구조를 가지는 뉴런과 유사하다는 것을 보여준다.
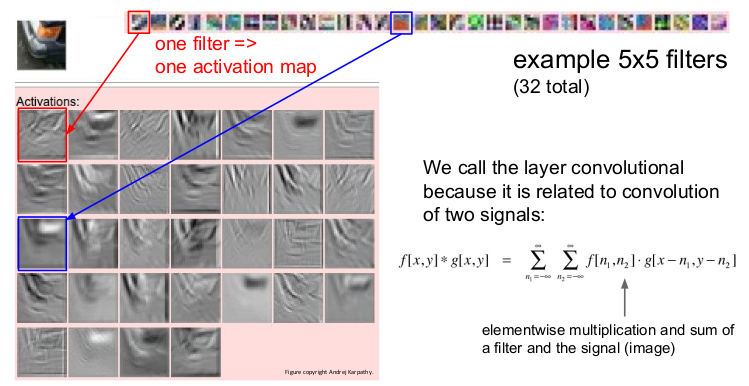
위의 그림은 32개의 5x5 필터를 통해 나온 32개의 activation map이 각각 어떻게 표현되는지를 시각적으로 보여준다. 1개의 필터는 1개의 activation map을 생성하고 입력 이미지의 특성을 1개 찾을 수 있다. 그 중 한 예로 파란 사각형으로 표시된 빨간색의 필터는 자동차의 범퍼 모양과 비슷한 이미지를 잡아내고 있는 것을 볼 수 있다.
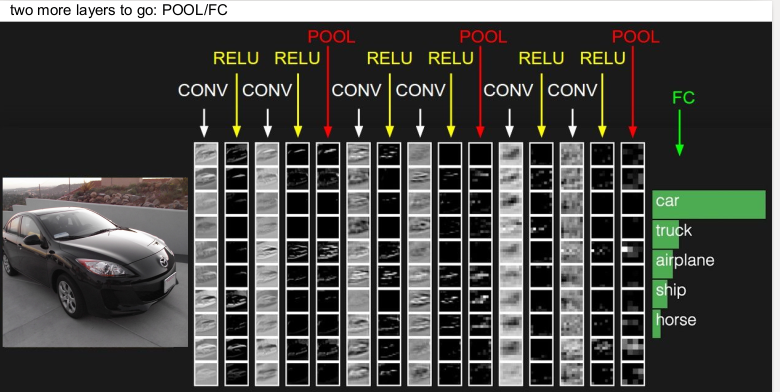
ConvNet의 각 층을 어떻게 쌓는지 한 예가 다음과 같다. Convolution layer에 활성함수인 ReLU를 쌓고, activation map의 크기를 줄여주는 pooling layer를 쌓는 방식을 여러 번 한 후, 마지막에 Fully connected layer를 쌓아 이미지를 클래스별로 분류한다. (여기서 행(column)은 volume이고 열(row)은 activation map이다.)
How to compute output size
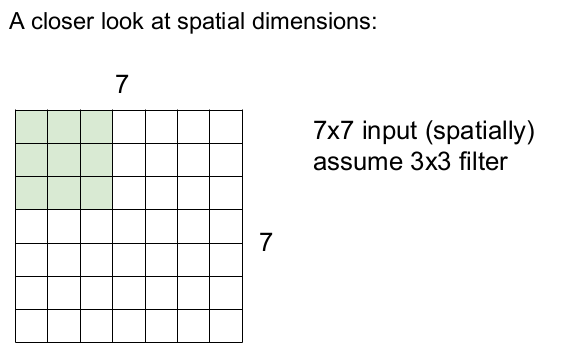
간단한 예를 통해 필터가 어떻게 입력 이미지를 슬라이딩하는지 설명할 것이다. 입력 이미지의 크기가 7x7이고 필터의 크기는 3x3이며, stride(보폭)을 1로 한다고 하자.
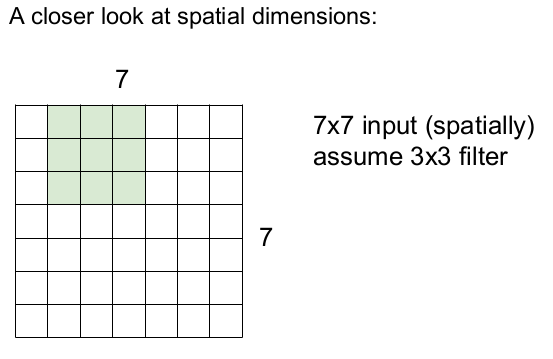
필터가 오른쪽으로 1칸씩 움직이면서 슬라이딩한다. 이런 식으로 오른쪽 끝까지 1칸씩 슬라이딩하고, 아래 칸으로 내려가 반복적으로 1칸씩 슬라이딩한다.
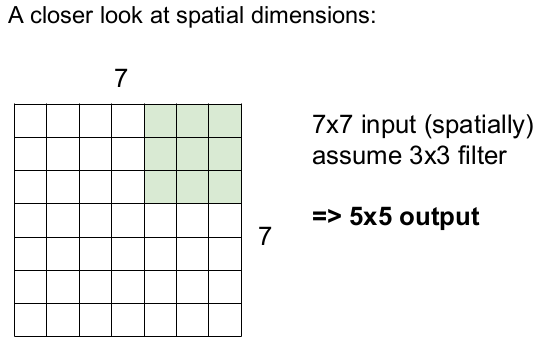
오른쪽 하단까지 오른쪽으로 5번씩, 밑으로 5번을 움직이므로 출력 이미지의 크기는 5x5이 된다.
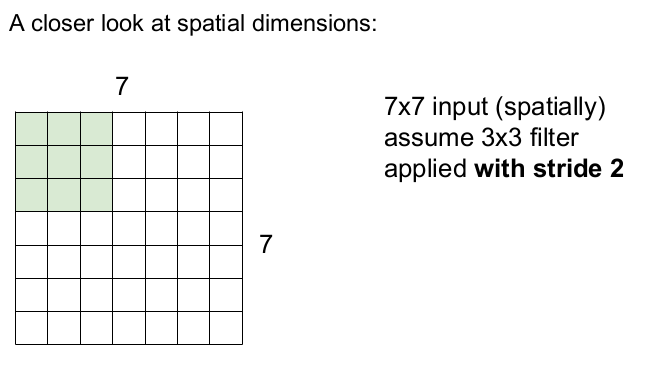
이제 3x3의 필터를 사용하고, 보폭을 2로 하여 슬라이딩해 보자. 오른쪽 끝까지 3번씩, 아래로 3번 슬라이딩하므로 3x3의 activation map이 나온다.
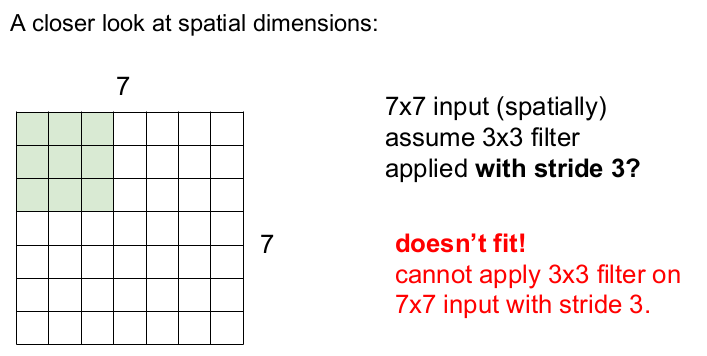
그렇다면 보폭이 3이 된다면 어떻게 될까? 오른쪽으로 2번 슬라이딩하면 1칸이 남고, 아래로도 1칸이 남는다. 따라서 보폭 3일 때는 7x7의 입력 이미지를 3x3 필터가 모두 슬라이딩할 수 없다.(오른쪽으로 1칸, 아래쪽으로 1칸이 남는다.) 따라서 불균형한 정보(정보의 일부가 누락)를 가진 activation map이 나온다.
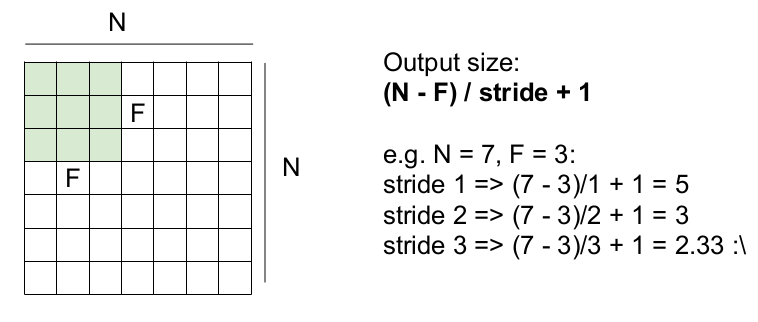
위의 식을 일반화하면 다음과 같다. NxN의 입력 이미지를 FxF의 필터가 stride만큼 슬라이딩할 때, 나올 수 있는 activation map의 크기는 (N-F)/stride + 1 이다. 그러나 여기서 보폭의 크기가 3이면 결과값이 2.33이 나오므로 보폭이 3이면 activation map이 잘 동작하지 않는다.
Zero Padding

이런 문제를 해결하기 위한 일반적인 방법은 입력 이미지에 zero padding을 하는 것이다. 즉 입력 이미지의 바깥에 0으로 이루어진 pixel을 붙여준다.
zero padding은 또한 출력 이미지의 크기를 유지시킬 수 있다. 7x7의 입력 이미지에 1개의 zero padding을 하면 3x3 필터, 보폭 1일 때 같은 크기, 즉 7x7의 activation map이 나온다. 일반화를 하면 보폭 1, FxF의 필터를 사용할 때, (F-1)/2개의 zero padding을 하면 입력 이미지와 같은 크기의 출력 이미지(activation map)가 나온다.
입력 이미지보다 작은 크기의 출력 이미지가 나오면 입력 이미지의 모서리(필터가 슬라이딩하지 못하는 부분)의 정보가 누락된다. 그러나 zero padding을 하면 입력 이미지의 모서리의 정보까지도 출력 이미지에 잘 전달할 수 있다.
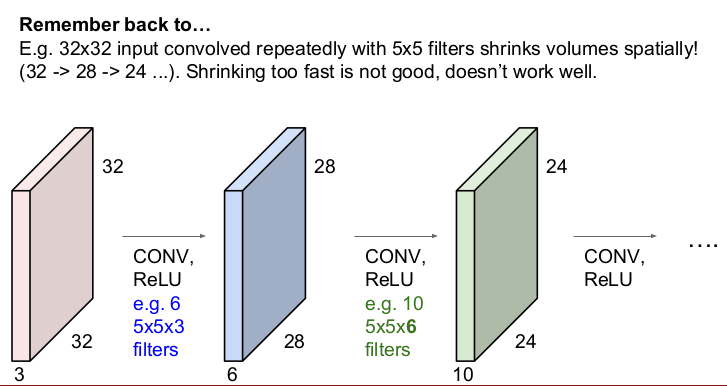
예를 들어 32x32의 입력 이미지에 5x5의 필터로 반복하여 슬라이딩하면 activation map(출력 이미지)의 크기는 28, 24, ... 이런 식으로 빠르게 줄어들 것이다. 이는 빠르게 정보가 손실된다는 것을 의미하므로 모든 Layer를 통과했을 때, 정확한 정보를 추출할 수 없다(입력 이미지 중간 값은 여러 번 반영되나 모서리의 정보는 손실되거나 적게 반영된다).
입력 이미지와 출력 이미지의 크기가 같게 하는 이유는 convolution layer를 거치면서 이미지의 크기가 준다고 하면, 거대한 신경망을 통과할 때 더이상 convolve할 수 없기 때문이다. 그래서 convolution layer에서는 zero padding을 하여 출력 이미지의 크기를 보존하고 이미지의 크기를 줄이는 것은 pooling에서 한다.
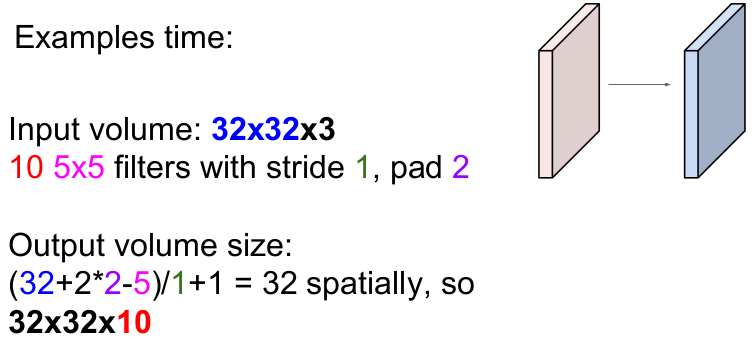
32x32x3의 입력 이미지에 2개의 zero padding을 한 후, 10개의 5x5 필터를 보폭 1씩 슬라이딩하면 출력 이미지의 크기는 어떻게 될까?
일반화된 식을 통해 계산하면 (N-F)/stride + 1 = (32+2*2-5)/1+1 = 32가 나온다. 또한 10개의 필터를 사용했으므로 필터의 depth는 10이다. 따라서 정답은 32x32x10이다.
이를 일반화하면 다음과 같다. NxN의 입력 이미지에 P만큼 zero padding을 한 후, K개의 FxF의 필터를 stride만큼 슬라이딩하면 A=(N+2*P-F)/stride + 1 이 나오고, K개의 필터이므로 총 activation map의 크기는 AxAxK이다.
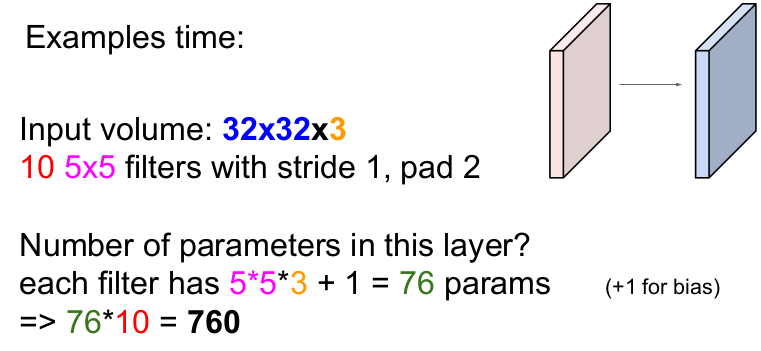
그렇다면 이 층에서 사용하는 파라미터의 수는 몇 개일까?
각 필터(depth가 3이므로 5x5x3의 필터)는 5 * 5 * 3 + 1(bias) = 76개의 파라미터를 가지고 필터의 개수가 10개이므로 76 * 10 = 760이다. 즉 이 층에서 사용하는 총 파라미터의 수는 760개이다.

정리하자면 ConvNet에 필요한 하이퍼파라미터는 필터의 수인 K, 필터의 크기인 F, 보폭인 S, zero padding의 수인 P이다. 여기서 필터의 개수인 K는 일반적으로 (32, 64, 128, 512)으로 정한다.
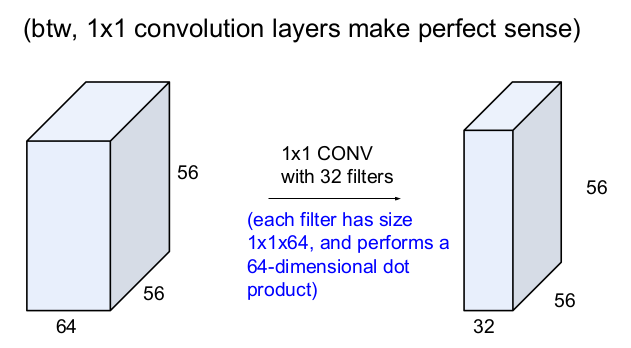
56x56x64의 입력이미지에 32개의 필터를 1x1 CONV한다는 것은 크기가 1x1x64인 64개의 필터가 있고 64차원 내적을 한다는 뜻이고, 그 결과로 56x56x32의 activation map이 나온다. 참고로 1x1의 convolution layer는 pooling과 비슷하다.
1x1xD의 convolution은 차원을 줄여주는 역할을 한다. 100x100x512의 입력 이미지를 D개의 1x1x512 필터로 convolve하면 출력 이미지의 크기는 100x100xD이 된다. D개의 1x1x512 필터는 수학적으로 FC layer와 같다. 다만 FC layer는 고정된 크기를 가지는 입력 이미지를 가지지만 convolution layer는 100x100과 비슷하거나 공간적으로 더 큰 입력 이미지를 받아들인다는 점이 다르다. 따라서 FC layer와 D개의 1x1x512 필터는 서로 대체할 수 있다. 따라서 D개의 1x1x512 필터가 네트워크의 마지막에 존재하면 FC layer와 같은 역할을 수행한다.
The neuron view of Conv Layer

뉴런의 관점으로 보면 Convolution Layer는 local connectivity(1구역은 1노드가 담당)를 가진 뉴런과 같다.
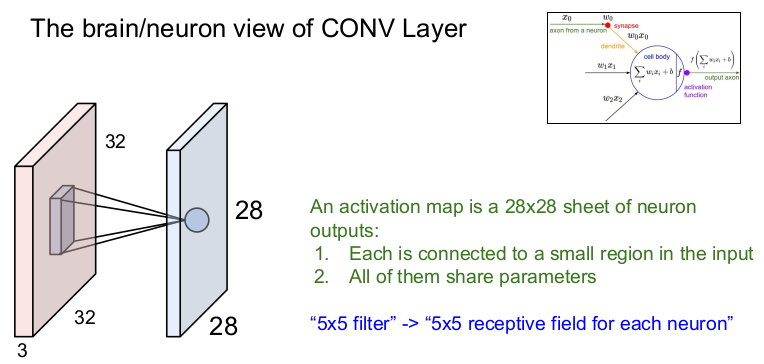
activation map은 28x28개의 뉴런 출력이고, 각각은 입력 이미지의 국소적인 부분과 연결된다. 또한 모든 부분은 동일한 파라미터를 공유한다. 5x5 필터는 각 뉴런의 5x5 수용체(receptive field)와 같다. 특정 부분만 처리하는 뉴런의 국소 지역 여러 개가 모여서 전체 이미지를 보게 되는 것과 비슷하다.
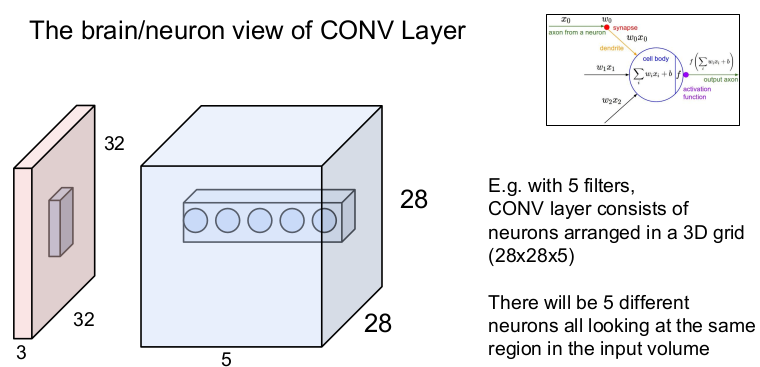
5개의 필터를 가진 CONV layer 는 28x28x5 안에 존재하는 뉴런으로 구성되어 있다. 5개의 뉴런들이 입력 이미지의 같은 부분을 모두 본다(그러나 가중치 W는 다르다). 즉 동일한 파라미터를 가진 5개의 필터는 입력 이미지의 같은 부분에 연산을 각각 1번씩, 총 5번을 하게 된다.
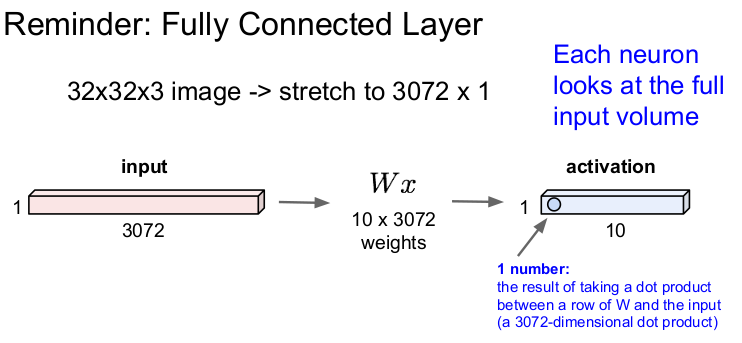
FC layer는 32x32x3의 이미지를 쭉 늘려 3072x1의 벡터로 만든 후, 가중치 W와 내적해 1개의 숫자(점수)를 추출한다. 뉴런의 관점에서 보면 각 뉴런이 전체 입력 이미지를 한 번에 보는 것과 같다.
정리하자면 Convolution layer는 입력 이미지를 국소적으로 여러 번 바라보고, FC layer는 입력 이미지를 전체적으로 1번 보는 것과 같다. Convolution layer는 작은 크기의 필터가 입력 이미지의 작은 부분을 슬라이딩하면서 내적하여 1개의 숫자를 얻는다. 그 후, 입력 이미지의 깊이와 같은 수의 필터가 입력 이미지의 같은 부분을 여러 번 내적하여 여러 개의 숫자를 얻는다. 이 숫자들이 모인 것이 activation map이다. 반면 FC layer는 입력 이미지를 늘려서 가중치와 1번 내적하여 하나의 숫자를 얻는다.
Convolution layer는 입력 이미지 일부분에서 특징을 추출하므로 전체 이미지에서는 여러 개의 특징을 추출한다. 따라서 이미지 확대, 축소, 이동해도 이미지의 특징을 잘 찾을 수 있다. 그러나 FC layer는 이미지 전체의 특징 하나를 추출하므로 효과적이지 않다.
The structure of CNN

위의 이미지는 자동차를 모델이 어떻게 하여 분류를 하는지를 보여준다. 입력 이미지가 convolution layer와 activation function RELU를 2번 반복하여 지난 후, Pooling layer를 통과해 차원을 줄여주는 과정을 여러 번 반복한 후, 마지막 FC layer를 통과하여 이미지가 어떤 것인지 1개의 숫자로 분류해 준다.
Pooling Layer
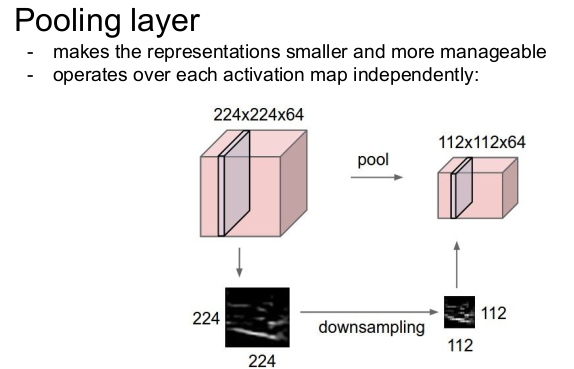
Pooling layer는 표현(representaions)를 작게 만들어(downsampling) 관리하기 쉽게 만들고(파라미터의 수가 줄어들기 때문에 관리가 쉽다), 각 activation map에 독립적으로 작용한다. 즉 이미지의 차원을 공간적으로 줄여준다. 주의할 점은 depth는 줄이지 못한다는 것이다. 또한 pooling할 때 padding하지는 않는다.
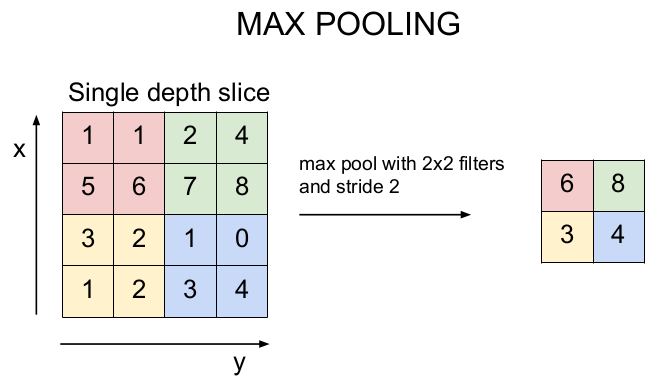
가장 많이 사용되는 것은 Max Pooling이다. 필터의 크기와 보폭을 선택하여 입력 이미지의 크기를 줄인다(downsampling).
2x2 필터를 보폭 2로 입력 이미지의 크기를 줄여보자. 필터 안에 존재하는 숫자 중 가장 큰 값을 선택하여 출력 이미지를 출력한다. 그림의 예를 설명하면, 붉은 부분에서 가장 큰 숫자는 6이므로 6을 뽑고, 푸른 부분에서는 8을 뽑고, 노란 부분에서는 3, 파란 부분에서는 4를 뽑아 6, 8, 3, 4의 출력 이미지를 얻을 수 있다.
pooling을 하면 출력 이미지의 크기가 줄어들기 때문에 정보를 잃는 것이 아닌가 생각할 수도 있지만 의도적으로 하게 되면 더 좋은 결과가 나올 수도 있다.

일반적인 파라미터 설정은 필터의 크기와 보폭의 크기가 2와 3일 때이다.

입력 이미지는 Convolution layer, ReLu, Pooling layer를 통과한 후, 마지막으로 FC layer를 통과한다. FC layer는 전체 입력 이미지와 연결되어 1개의 숫자를 출력한다. 즉 이미지를 1개의 클래스로 분류한다(이미지 분류기).
CIFAR-10으로 직접 실험해 볼 수 있다. http://cs.stanford.edu/people/karpathy/convnetjs/demo/cifar10.html
Summary

ConvNets은 CONV, POOL, FC layer가 모여 만들어진다. convolution layer는 파라미터를 많이 사용한다.
