• 스탠퍼드 대학의 CS231n: Convolutional Neural Networks for Visual Recognition
  본 포스팅은 CS231n의 내용을 정리한 것이다. 이곳에 출처가 따로 언급되지 않은 이미지들은 스탠퍼드 대학에서 제공하는 강의 슬라이드에서 가지고 왔다.
  [CS231n] http://cs231n.stanford.edu/2017/syllabus.html

강의에 들어가기에 앞서 지난 시간에 배운 Convolational Neural Networks에 대한 질문에 대한 설명을 정리하려고 한다.

• 질문: 케라스 conv2d와 CNN과의 관계
  tf.keras.layer.conv2d(10, 5, padding='same', input_shape=input_volume[1,32,32,3]
  10은 필터의 개수, 필터의 크기(5x5, 대체로 정사각행렬이므로 1개만 표시), input
  _shape은 입력 이미지의 정보이다. 1은 입력 이미지의 개수, 32, 32는 입력 이미지의 크기(5x5), 3은 3차원(RGB, 즉 입력 이미지의 depth)을 의미한다. stride = 1이 default이고, 필터 5x5x3에서 3은 케라스에서 입력 이미지의 depth와 자동으로 맞춰주므로 생략한다.

CNN에서 생각할 점

max pooling을 쓰는 이유는 입력 이미지의 가장 큰 특징을 추출하기 위해 가장 큰 값을 뽑는 것이다. 그러나 최근에는 global average pooling을 자주 사용하기도 한다.

Training Neural Networks (1)

강의를 나가기에 앞서 지난 시간 복습을 간단히 한다. 행렬의 backpropagation은 강의 노트 4에 보면 자세히 설명되어 있다. n-layer Neural Networks는 선형 함수 사이에 비선형 함수
(활성화 함수)를 끼어 넣는 것이다. Convolutional Neural Networks는 spatial structure를 유지하면서 학습한다.

최적화(optimization)을 통해 가중치(파라미터)를 업데이트한다.

Mini-batch SGD는 다음의 과정을 반복한다.
1. 데이터의 일부를 샘플로 뽑는다.
2. 그래프(네트워크)를 통과하면서 계산하여 Loss를 얻는다.
3. 그래디언트를 계산하기 위해서 backpropagation을 한다.
4. 그래디언트를 사용하여 파라미터를 업데이트한다.

Training Neural Networks

이번 시간과 다음 시간에는 NN의 학습에 대해 배울 것이다.

이번 시간에 처음 NN학습을 시작할 때 필요한 기본 설정에 대해 알아볼 것이다. 이 포스팅에서는 Activation Functions, Data Preprocessing, Weight Initialization을 다룰 것이다.

Activation Functions

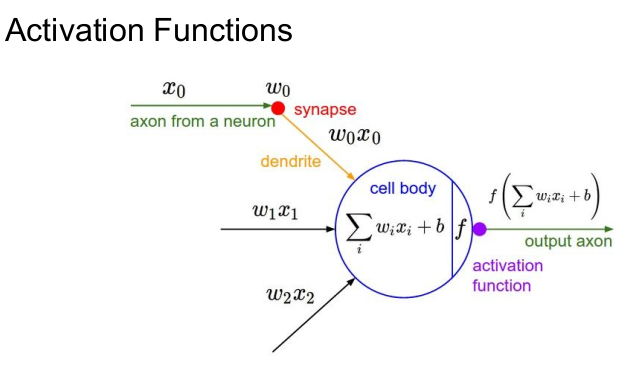
Neural Network의 모습을 그림으로 표현한 것이다. 각 뉴런에서 전달된 입력값 $x_i$이 $w_i$와 곱한 것을 모두 합하고(선형) 바이어스(bias)를 더한 후(즉 FC/CNN을 거친 후) 비선형 함수인 활성화 함수와 연산하여 다음 뉴런으로 나가는 모습이다. 그 중 지금 우리의 관심은 활성화 함수(Activation Function)이다.

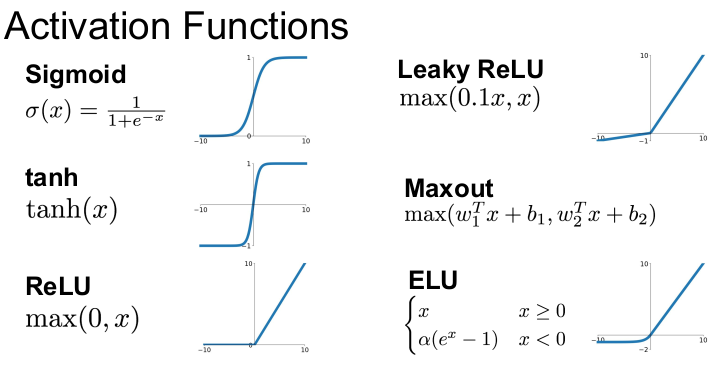
활성화 함수의 종류는 위와 같이 다양하다. 활성화 함수는 모두 비선형 함수이다.

sigmoid 함수

가장 먼저 살펴볼 것은 sigmoid 함수이다. sigmoid 함수는 넓은 범위의 값을 [0,1] 사이의 값으로 만든다(squash). 따라서 입력값이 크면 1에 가깝고, 입력값이 작으면 0에 가까워진다. 0과 1 사이의 값은 선형 함수와 같은 모양을 띈다. 뉴런의 "firing rate"를 saturation(포화)시키는 것으로 여겨졌기 때문에 역사적으로 많이 사용되었다. (즉 지금은 사용하지 않는다.) 어떤 값이 0에서 1사이의 값을 가지면 이를 firing rate라고 생각할 수 있다.

그러나 sigmoid 함수는 3가지의 문제점을 갖고 있다. 첫 번째 문제점은 포화된 뉴런(0이나 1에 가까운 값을 내는 뉴런)이 그래디언트를 "죽인다"는 것이다(vanishing gradient 문제).

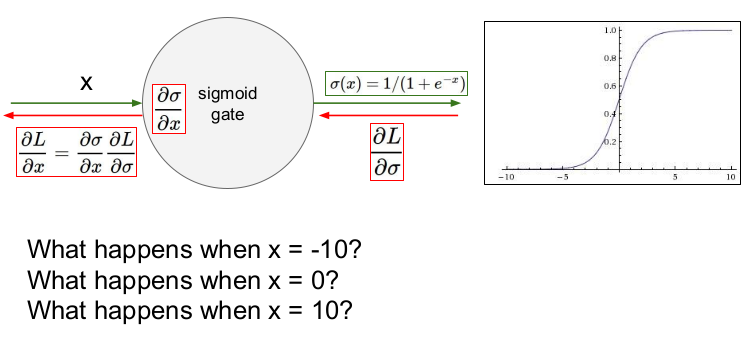
sigmoid 함수의 computational graph를 보자. Backprop에서 Gradient는 어떻게 될까? $\frac{\partial L}{\partial σ}$가 sigmoid gate에 들어가면 밑으로 내려가고, $\frac{\partial x}{\partial σ}$와 곱해진다. 이 값이 local sigmoid function의 gradient($\frac{\partial L}{\partial x}=$$\frac{\partial L}{\partial x}$$\frac{\partial x}{\partial σ}$)가 된다. 이런 값들이 연쇄적으로 이런 값들이 계속 연쇄적으로 Backporp될 것이다.

따라서 x=-10일 때 그래디언트는 0이 된다. backpropagation을 할 때, sigmoid gate에 들어오는 그래디언트 $\frac{\partial L}{\partial σ}$=0이므로 로컬 그래디언트도 0이 되고, 그 뒤에 전달되는 모든 그래디언트는 0이 된다.
x=0일 때는 backpropagation이 잘 되어 그럴듯한 그래디언트가 나온다.
x=10일 때도 x=-10일 때와 같이 sigmoid가 flat하므로 그래디언트는 다 죽는다.
따라서 x가 아주 큰 양수이거나 아주 작은 음수일 때(포화 지점), 0인 그래디언트를 계속 전달하므로 그래디언트를 모두 죽인다.

sigmoid 함수의 두 번째 문제점은 sigmoid 함수의 출력값이 0을 중심으로 하지 않는다(not zero-centered)는 점이다.

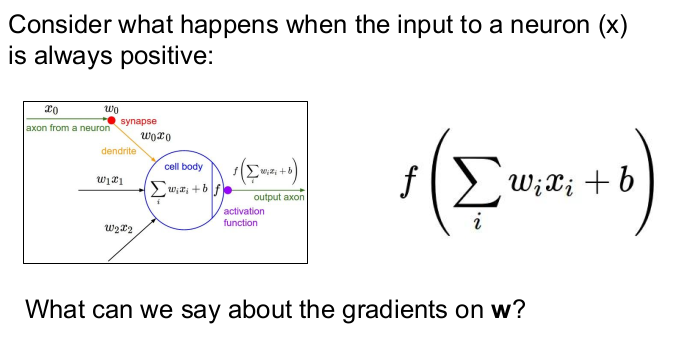
Neural Network의 그림을 통해 설명하자. 뉴런(x)에 대한 입력값이 항상 양수이면 $w$에 대한 그래디언트는 어떻게 될까?

$w_ix_i + b$이 활성화 함수 $f$를 통과하면 $f(\sum_i w_ix_i + b)$이 된다. 그런데 sigmoid 함수는 항상 양수의 출력값을 가지므로 sigmoid 함수를 한 번 거친 입력값은 항상 양수이다. backpropagation할 때, local gradient를 생각해보자. $\frac{\partial L}{\partial f}$를 우선 계산한다. local gradient는 x이다. $\frac{\partial L}{\partial f}$의 값은 음수 또는 양수가 된다. 그 이유는 임의의 gradient가 내려올 때, local gradient와 곱해지고, $\frac{\partial f}{\partial w_i}$는 x가 될 것이다. 그렇게 되면 gradient의 부호는 위에서 내려온 gradient의 부호와 같아진다. 이는 W가 모두 같은 방향으로만 움직인다는 것을 의미한다.

$w$가 모두 같은 방향으로 이동하므로 parameter update할 때도 다같이 증가하거나 감소한다. 이 gradient 업데이트는 매우 비효율적이다. $w$의 이차원 예제를 살펴 보자. $w$에 대한 2개의 축으로 이루어져 있다. 전부 양수나 음수로 업데이트된다는 뜻은 그래디언트의 이동 방향이 4분면 중 두 영역(양수이거나 음수이라는 뜻이다. 즉 두 방향으로만 그래디언트가 업데이트한다. 위의 그림에서 파란색 선은 $w$이 바람직하게(optimal $w$) 움직이는 모습이다. 그러나 양수나 음수로만 움직이는 $w$는 빨간 선과 같이 지그재그로 움직인다. 양수나 음수의 한 가지 방향으로만 움직이므로 파란색 방향으로는 내려갈 수 없다. 따라서 우리는 여러 번 그래디언트 업데이트를 수행해야 한다. 이런 이유로 우리는 zero-mean data(정규화된 데이터)를 추구하게 된다. 왜냐하면 x값이 양수와 음수 모두 가지므로 그래디언트가 전부 한 방향으로만 움직이지 않기 때문이다.

• 참조: [시그모이드 활성함수]https://nmhkahn.github.io/NN
  
  sigmoid 함수의 세 번째 문제점은 exp()의 계산 비용이 비싸다는 것이다(계산이 오래 걸림).

tanh(x) 함수

따라서 이 문제를 해결 하기 위해 tanh(x) 함수(hyperbolic tangent function)가 사용되었다. tanh(x) 함수는 입력값을 [-1, 1] 사이로 만들며, 0을 중심(zero-centered)으로 하는 함수이다. 그러나 그래프에서 볼 수 있듯이 큰 양수나 작은 음수일 때는 그래프가 평평해진다. 즉 뉴런이 포화되었을 때 그래디언트를 죽인는 문제점이 있다.

ReLU

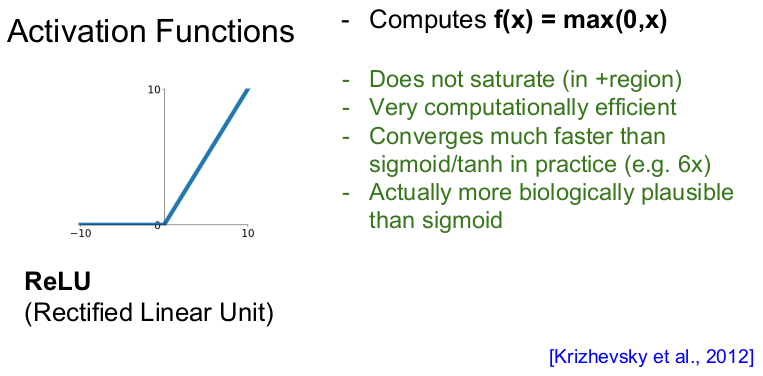
그래서 나온 활성화 함수가 ReLU이다. ReLU는 이전에 나왔던 활성화 함수의 문제점을 해결한다. ReLU는 양수일 때 뉴런이 포화되지 않아 그래디언트가 죽지 않으며(가장 큰 장점), 계산적으로 매우 효율적이다($f(x)=max(0,x)$이므로 계산이 빠르다). 수렴 속도도 sigmoid나 tanh 함수보다 6배 정도 빠르다. 또한 생물학적으로도 sigmoid 함수보다 타당도가 높다. 즉 실제 뉴런을 관찰했을 때, ReLU스럽다. 참고로 ReLU는 ImageNet 2012에서 우승한 AlexNet이 처음 사용하였고 현재 가장 많이 쓰이는 활성화 함수이다.

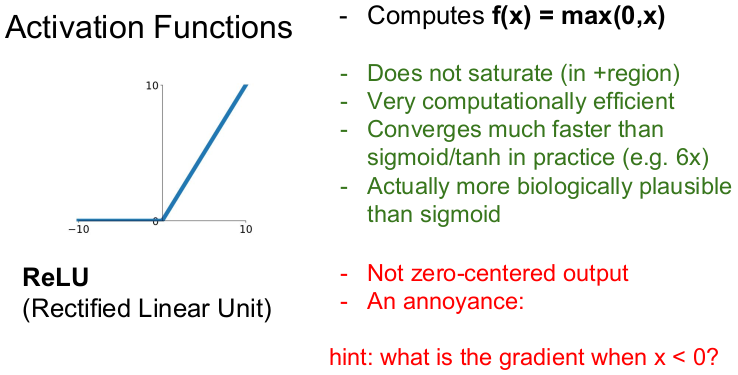
그러나 ReLU에도 문제점은 있다. 우선 ReLU의 출력값이 0을 중심으로 하지 않는다(not zero-centered). (그러나 이 문제는 vanishing gradient 문제보다는 덜 중요하다. 따라서 ReLU를 자주 사용한다.) 또한 $x<0$일 때, 그래디언트가 죽는다.

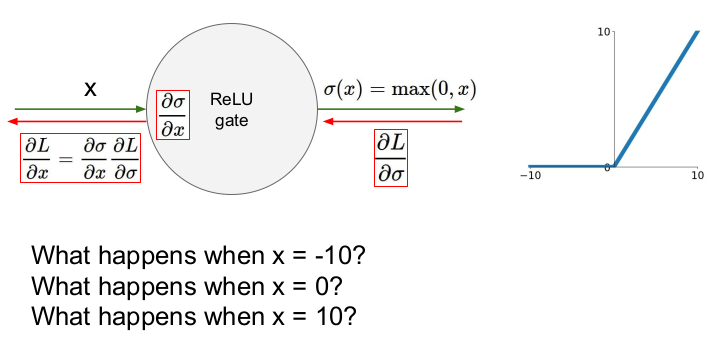
ReLU는 음수일 때는 포화되기 때문에 x=-10일 때 그래디언트가 0이 된다. 반면 x=10일 때는 그래프가 선형이므로 제대로 동작한다(그래디언트=1). x=0일 때는 그래디언트가 이론적으로는 정의되지 않으나 실제 연산으로는 0이 된다. 즉 ReLU는 절반의 그래디언트를 죽인다(dead ReLU).

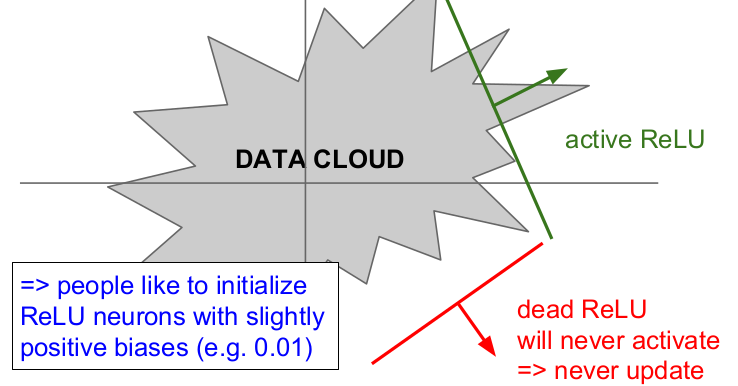
그래디언트를 절반만 죽이는 dead ReLU현상을 그림을 통해 설명한다. Data Cloud은 training data이고 초록색 선과 빨간색 선(평면)은 각 ReLU이다. ReLU가 Data Cloud와 겹치지 않을 경우에는 dead ReLU가 발생할 수 있다. dead ReLU에서는 activate가 일어나지 않고 업데이트 되지 않는다. 반면 active ReLU에서는 일부는 activate되고 일부는 activate되지 않는다.

dead ReLU가 발생하는 경우는 2가지인데, 첫 번째 경우는 가중치의 초기화가 잘못되어 가중치 평면이 Data Cloud와 멀리 떨어져 있을 때이다. 이 때는 ReLU가 절대 활성화(activate)되지 않고, gradient가 절대 업데이트 되지 않는다.

두 번째이자 더 흔한 원인은 learning rate가 너무 클 때이다. learning rate가 너무 크면 처음에는 적절한 ReLU로 시작해도 업데이트가 너무 크게 되므로 ReLU가 Data Cloud에서 벗어난다. 그래서 처음에는 학습이 잘 되다가 갑자기 죽어버리는 경우가 생긴다. 실제로 ReLU를 사용할 때는 10-20%가 dead ReLU가 된다. 그러나 이 정도는 네트워크 학습에 크게 영향을 미치지 않는다.

입력값이 모두 양수라면 0의 오른쪽 지역으로 들어오게 되고, saturation의 가능성이 있다. 왜냐하면 양수 지역에도 평평한 곳이 존재하기 때문이다. 그래서 사람들은 ReLU 뉴런에 작은 양수인 bias를 주어 초기화하여 dead ReLU를 방지하기도 한다. (그러나 별 성과는 없기 때문에 대부분 zero-bias로 초기화한다.)

Leaky ReLU / PReLU

ReLU의 문제점을 해결하기 위해 Leaky ReLU가 나왔다. Leaky ReLU는 어떤 곳에서도 뉴런이 포화되지 않으며 계산도 효율적으로 할 수 있다. 수렴 속도도 sigmoid나 tanh 함수보다 6배 정도 빠르며 어느 곳에서도 그래디언트가 죽지 않는다(그래프가 평평하지 않으므로).

다른 예시인 PReLU는 negative space에 기울기가 있다는 점에서
Leaky ReLU와 유사하나 backpropagation으로 기울기 α를 결정하므로 Leaky ReLU보다 유연하다.

ELU

또다른 예시인 ELU는 ReLU와 Leaky ReLU의 중간이라고 생각하면 된다. ELU는 ReLU의 모든 장점을 가진다. zero mean에 가까운 출력값을 가진다. 또한 ELU는 음수 지역에서 포화되지만 이 saturation이 좀더 noise에 강인하다. 이런 deactivation이 좀더 강인함을 줄 수 있다고 주장한다. ELU의 논문에서 타당성을 다양하게 제시한다. 그러나 복잡한 exp()(비싼 연산)을 계산해야 한다는 단점이 있다.

Maxout "Neuron"

Maxout "Neuron"은 ReLU와 Leaky ReLU를 일반화시킨 활성화 함수이다. $w_1^Tx + b_1, w_2^Tx + b_2$의 최대값으로 구하기 때문에 선형적인 지역이 나타나므로 뉴런이 포화되지 않고 그래디언트도 죽지 않는다. 그러나 뉴런당 파라미터가 2배가 된다는 단점이 있다.

결론

결론은 learning rate를 주의하면서 ReLU를 사용하라 이다. (다만 learning rate를 조심스럽게 결정해야 한다.) 다른 활성화 함수(ReLU의 변형)를 사용해도 되나 sigmoid 함수는 사용하지 않는 것이 좋다.

참고: 최근 자연어처리에서는 GELU를 많이 사용한다. 여기서 G는 gaussian이며 BERT, GPT-x에서도 사용하였다.

Data Preprocessing

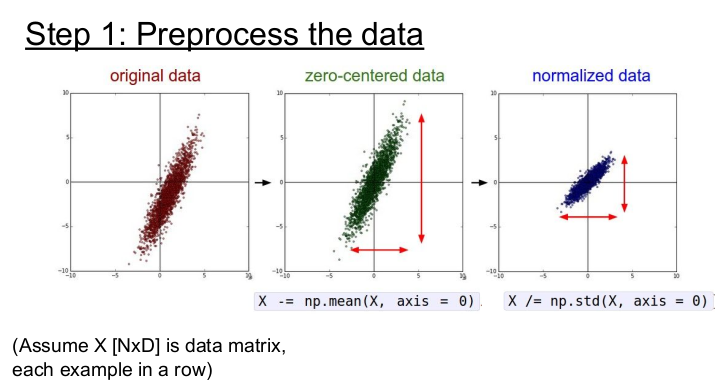
데이터 전처리의 방법은 (1) zero-centered data로 만들거나(데이터를 전체의 평균값으로 빼줌) (2) 정규화(normalized data)를 한다(데이터를 표준 편차로 나눔).

우선 데이터를 zero-centered data로 만드는 이유는 sigmoid 함수에서 살펴보았던 것과 같은 이유이다. (입력이 모두 양수/음수인 경우 모든 뉴런이 양수/음수인 그래디언트를 얻는다.)

정규화를 해주는 이유는 모든 차원이 동일한 범위 안에 있게 해주어 전부 동등한 기여를 하게 한다.

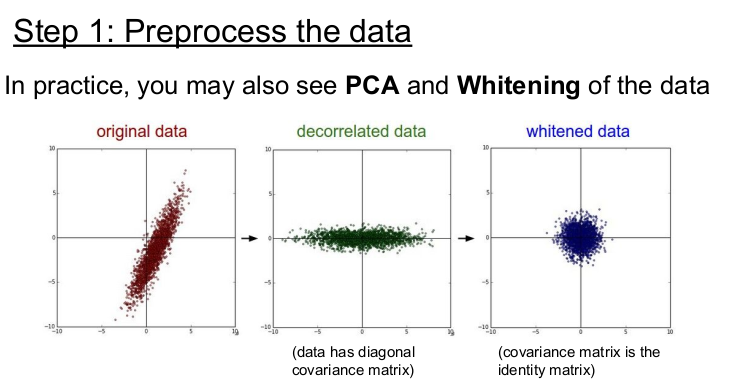
PCA(주성분 분석, 비지도 학습에서 사용)나 whitening은 통계적 학습에 적합하므로 이미지 분석에서는 잘 사용하지 않는다.

그러나 이미지 분석에서는 정규화는 할 필요가 없이 zero-centered 데이터로만 만들면 된다. 입력 이미지는 각 차원이 이미 특정 범위 안에 들어있기 때문이다. 이미지 처리는 원본 이미지 자체의 spatial 정보를 이용하여 이미지의 spatial structure를 얻는다.

학습 데이터를 전처리하면 평가 데이터에서도 동일하게 적용된다. 학습 데이터에서 구한 평균을 그대로 사용한다.

[32, 32, 3]의 이미지를 가진 CIFAR-10로 설명하자. 첫 번째 방법은 학습 데이터의 평균 값을 학습 데이터와 평가 데이터에서 빼는 것이다.

두 번째 방법은 채널마다 평균을 독립적으로 계산하여 채널 별로 평균을 빼준다. VGGNet의 경우는 RGB별로 평균을 구하여 학습데이터와 평가 데이터의 각 채널에서 뺐다. 우리의 판단에 따라 어떤 것을 사용할 지 결정하면 된다. (두 번째 방법이 계산이 편함)

학습 데이터 전체로 평균값을 구한다. mini-batch로 학습해도 평균은 학습 데이터 전체로 계산한다. 실제로 batch나 전체 데이터나 결과는 같다. 따라서 매우 큰 데이터의 경우는 작은 샘플링으로 평균을 구할 수도 있다.

그러나 이미지 전처리는 sigmoid에서의 문제점을 해결할 수는 없다. sigmoid에서는 zero-mean이 필요한데, 이미지 전처리는 첫 번째 레이어에서만 zero-centered 문제를 해결하고, 다음 레이어부터는 같은 문제가 반복된다. 따라서 Deep Network에서는 점점 더 non-zero centered될 것이다.

Weight Initialization

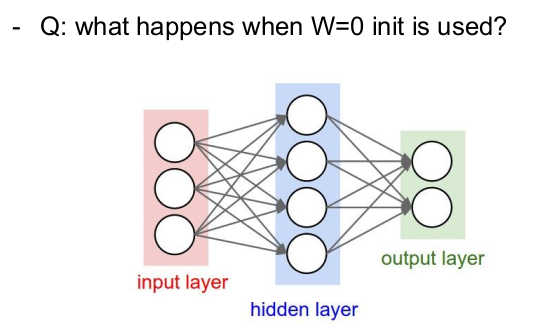
이제 가중치를 어떻게 초기화시켜야 하는지 알아보자. 2-layer neural network를 예를 들어 가중치 업데이트를 해보자.초기화된 $w$로 그래디언트를 구하고 그 그래디언트를 이용하여 $w$를 업데이트한다. 우선 가중치를 0으로 초기화하면 어떻게 될까?

만약 모든 $w$=0이면 동일한 $w$를 사용하므로 모든 뉴런이 같은 일(연산)을 하게 된다. 따라서 출력값은 모두 같고 그래디언트도 모두 같게 되어 같은 가중치값으로 업데이트된다. 그러나 우리는 뉴런이 다르게 생기기를 원한다. (symmetric breaking이 발생하지 않는다. 모델이 같은 결과를 낸다.)

Q. 그래디언트가 가중치 뿐 아니라 Loss의 영향도 받으므로 각각의 그래디언트는 다르지 않느냐?

뉴런이 어떤 클래스에 연결되느냐에 따라 뉴런은 다른 loss를 가질 수는 있다. 그러나 뉴런 전체를 보면 뉴런이 동일한 $w$로 연결되기 때문에 출력값과 그래디언트는 같은 값을 같는다.

초기화 문제를 해결하는 첫 번째 방법은 임의의 작은 값으로 초기화하는 것이다. 0을 평균으로 하고 0.01이 표준 편차인 가우시안 정규분포에서 초기 w를 샘플링하자. (앞으로의 모든 실험에서 이 조건을 사용한다). 즉 가우시안 정규분포에서 랜덤하게 고른 작은 값(표준편차를 0.01로 만듬)으로 초기화해보자. 이 경우, 작은 네트워크에서는 작동(symmetry breaking)하나 깊은 네트워크에서는 문제가 생긴다.

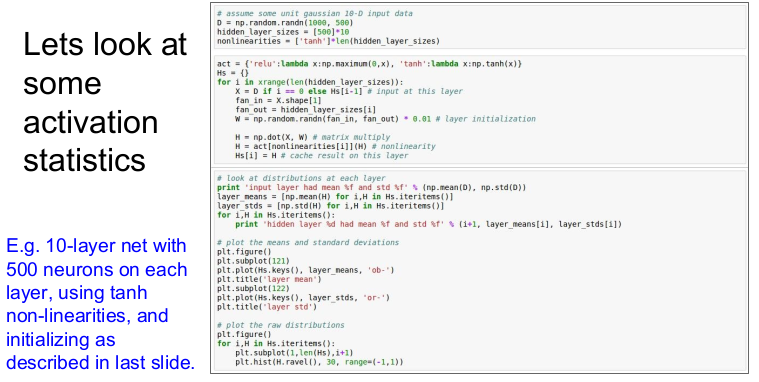
각 층에 500개의 뉴런을 가진 10개 층을 가진 네트워크를 가정하자. 랜덤하게 고른 작은 값($w=0.01$)으로 초기화하고, 활성화 함수로 tahn 함수를 사용하였다.

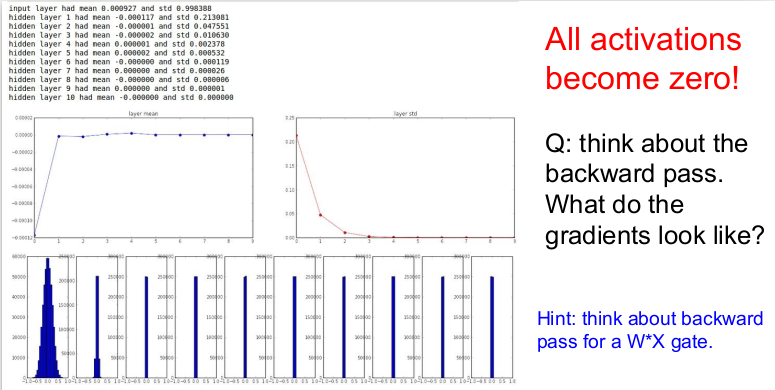
데이터를 랜덤으로 만들고 이 데이터를 forward pass시키고 각 레이어별 activation 수치를 통계화 시키면 1번째 층에서부터 평균이 0에 가깝게 나타난다는 것을 볼 수 있다(tanh 함수가 zero-centered이므로). 그러나 표준편차가 빠르게 0에 수렴하는 것을 볼 수 있다.

가운데 그래프는 레이어당 평균과 표준편차를 나타낸 것이고, 맨 밑에 같은 결과를 분포로 표현했다. 아래쪽의 분포를 보면 1번째 층에서는 좋은 분포를 보이나 $w$가 너무 작으므로 결과값이 급격히 작아져서 모든 activation(출력값)이 결국 0이 되는 것을 볼 수 있다. 즉 모든 활성함수 결과는 0이 된다. 그렇다면 backward pass할 때, $w$에 대한 그래디언트는 어떻게 될까?

각 층의 입력값이 매우 작으므로 입력값은 층을 지날수록 점점 0에 수렴한다. 전파된 upsream gradient와 locat gradient인 $x$를 서로 곱하여 그래디언트를 업데이트하는데, $x$이 너무 작으면 업데이트되는 그래디언트도 점점 작아지고, 결국 0으로 수렴한다. 따라서 그래디언트는 업데이트되지 않는다. 이 실험은 그래디언트의 흐름이 네트워크에 어떤 영향을 미치는지 생각해 볼 수 있는 좋은 예시이다. 따라서 forward pass의 흐름을 보고 gradient가 어떻게 전파되는지 짐작할 수 있다. 또한 다양한 입력 타입에 따라 가중치와 그래디언트가 어떤 영향을 미치는지도 생각해 볼 수 있다.

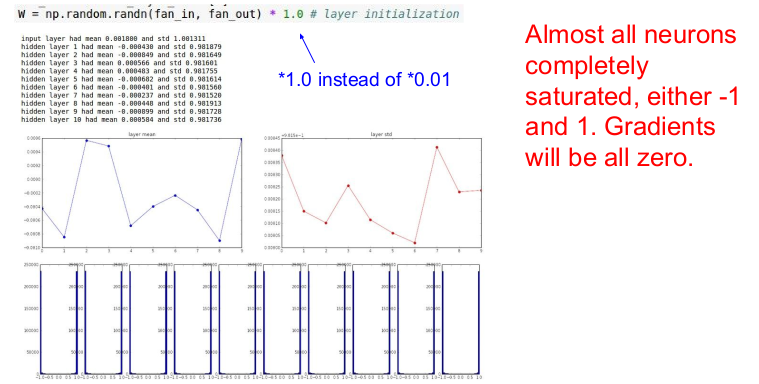
그렇다면 $w$를 크게 하면 어떻게 될까? 두 번째로 $w$에 0.01대신 $w=1$을 넣어 가중치 $w$를 초기화해 보자. 가중치가 큰 값을 가지므로 비선형 함수인 $tanh(xw)$의 결과값이 포화(saturated)되어 출력값이 거의 모두 -1이나 1이 된다. 따라서 그래디언트는 0이 되어 $w$이 업데이트되지 않을 것이다.

이처럼 적절한 $w$를 구하는 것은 어렵다. 너무 작으면 사라지고, 너무 크면 포화된다. 그렇다면 어떻게 $w$를 초기화해야 할까?

Xavier initialization

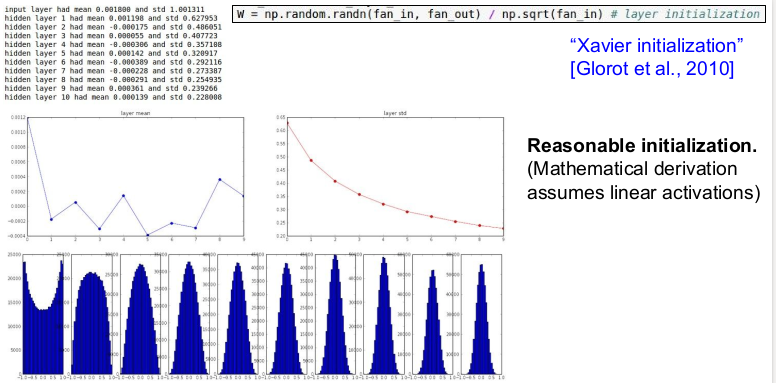
합리적인 $w$를 찾을 수 있는 좋은 방법 중 하나는 Xavier initialization 를 사용하는 것이다. Xavier initialization는 가우시안 표준 정규 분포에서 랜덤으로 뽑은 값을 "입력의 수"로 스케일링해준다. Xavier initialization는 입/출력값의 분산을 맞춰주는 것이다. 따라서 입력의 수가 작으면 작은 값으로 나눠주어 큰 값을 얻는다. 그리고 더 큰 가중치 $w$를 필요로 한다. 그 이유는 작은 입력의 수가 가중치와 곱해지므로 가중치가 더 커야만 출력의 분산만큼 큰 값을 얻을 수 있기 때문이다. 반대로 입력의 수가 많아지면 작은 가중치 $w$를 필요로 한다. (자세한 내용은 lecture note를 확인하자.)

각 레이어의 입력을 unit gaussian이길 원하면 이 초기화 기법을 사용할 수 있다. 여기서 가정하는 것은 linear activation이 있다고 가정하는 것이다. tanh의 경우 tanh의 active region 안에 있다고 가정한다는 뜻이다.

ReLU를 사용할 때의 weight initialization

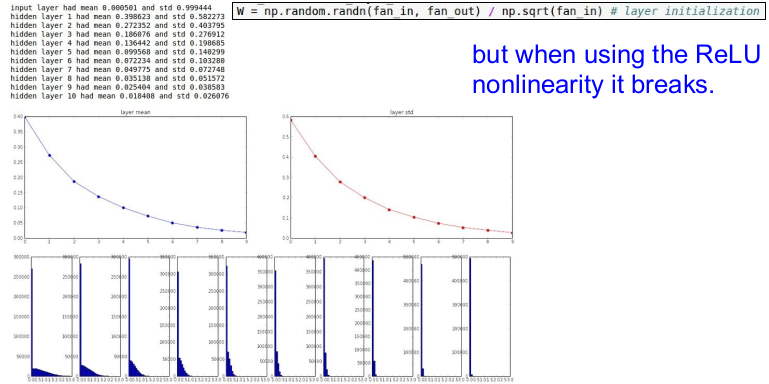
그러나 Xavier initialization는 ReLU를 사용할 때는 잘 동작하지 않는다(dead ReLU 발생). ReLU의 출력값의 절반이 0이 되기 때문에 출력값의 분산도 절반이 되기 때문이다. 따라서 이전의 가정을 하고 ReLU를 사용하면 $w$이 매우 작아지고 결국 그래디언트가 0이 되어 비활성화된다.

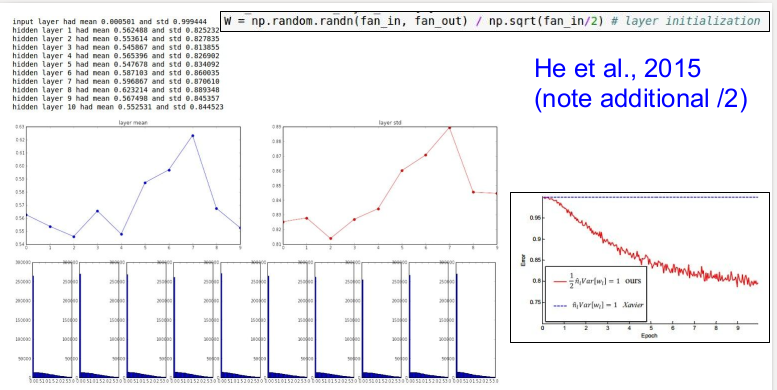
이런 문제를 해결하기 위해서 He 등은 뉴런의 절반이 사라지는 것을 고려하여 입력데이터의 개수를 2로 나누는 것을 Xavier initialization에 추가하였다. 이는 매우 견고하여 결과값을 계속 유지한다. 위의 그래프를 보면 잘 동작하는 것을 볼 수 있다(좋은 분포 보임).

이 실험을 통해 작은 변화가 학습에 큰 기여를 하는 것을 알 수 있다.

적당한 초기화값을 찾는 것은 활발히 연구되고 있다. 연구되고 있는 다양한 가중치의 초기화 방법을 사용할 수 있으나 먼저 Xavier initialization를 써보고 다른 초기화 방법을 사용하자.