경사하강법 최적화 알고리즘 (Gradient Descent)

• 경사하강법은 목적 함수의 기울기와 반대 방향으로 파라미터를 업데이트하여 목적 함수를 최소화하는 방법
• 학습률은 (로컬) 미니멈에 도달하기 위해 우리가 취한 스텝의 사이즈를 결정함
• 우리는 골짜기에 도달하기 위해 목적함수의 경사 방향을 따라감

An overview of gradient descent optimization algorithms 살펴보기

경사하강법 변형

1. Batch(Vanila) GD

모든 데이터셋에서 각 스텝마다 Gradient 계산을 진행하며 계속 파라미터 업데이트를 함

• 장점 : 특성 수에 민감하지 않음
• 단점
  1. 메모리에 맞지 않는 데이터셋을 다루기 어렵고 매우 느릴 수 있음
  2. 온라인 상에서 모델을 적용하는 것은 적합하지 않음

for i in range(nb_epochs):
	params_grad = evaluate_gradient(loss_function, data, params)
    params = params - learning_rate * params_grad

위 알고리즘에서 알 수 있듯이 각 Epoch마다 손실 함수에서 파라미터를 계산해 최신의 상태를 유지하고자 하는 것을 알 수 있다. 이러한 특성 때문에 수행해야 하는 과정이 굉장히 많다. 따라서, 글로벌 최솟값과 지역 최솟값을 탐색하고 찾는 것은 보장할 수 있다는 특징이 있다.

2. Stocastic GD

• SGD는 경사를 다시 계산해 대규모 데이터 세트에 대해 중복 계산을 수행함
• 각 파라미터 업데이트 전에 유사한 예로부터 중복성을 제거함
• 한 번에 하나의 업데이트를 수행
• 온라인 학습에도 사용가능하고 일반적인 Batch GD보다 더 빠름

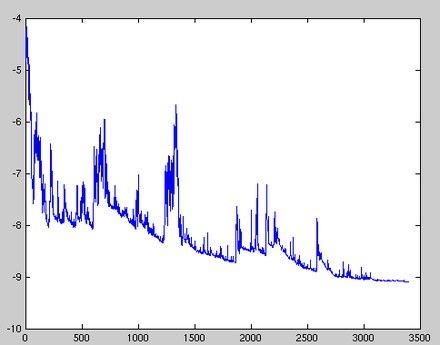
• 위 그림처럼 목적 함수가 크게 변동하도록 하는 높은 분산으로 빈번하게 업데이트를 수행함
• SGD가 계속 오버슈팅할 경우 정확한 최솟값으로 수렴하는 과정을 복잡하게 함
• 학습률을 천천히 낮추면 SGD는 배치 경사하강법과 동일하게 움직임
  

for i in range(nb_epochs):
	np.random.shuffle(data)
    for example in data:
    	params_grad = evaluate_gradient(loss_function, example, params)
        params = params - learning_rate * params_grad

코드를 보면 각 Epoch마다 데이터를 섞어서 최적해를 찾고 있다. 그리고 데이터 마다 Gradient를 계산해 업데이트를 진행하는 모습을 볼 수 있다.

3. Mini-batch GD

• Mini-batch는 SGD를 발전시켜 하나의 데이터가 아닌 하나의 데이터 셋을 기준으로 Gradient를 계산함
• 임의의 샘플에 대해 계산할 경우 파라마터의 분산을 줄여 더 안정적 수렴을 기대할 수 있음
• 일반적 미니 배치 사이즈는 50~256이지만 Neural Network를 계산하는 과정에서 달라질 수 있음

for i in range(nb_epochs):
	np.random,shuffle(data)
    for batch in get_batches(data, batch_size=50):
    	params_grad = evaluate_gradient(loss_function, batch, params)
        params = params - learning_rate * params_grad

함수 식은 SGD와 비슷하나 SGD는 각 데이터마다 돌아다니며 중복을 제거하지만 Mini-batch는 사이즈를 정해서 "데이터 셋"을 순환하는 모습으로 서로 다름을 알 수 있다.

어려움 (Challenges)

경사하강법을 적용할 경우 좋은 수렴을 보장하지만 여러 문제에 직면하게 된다.

1. 적절한 학습률을 선택하기 어려움

• 학습률이 너무 작은 경우 너무 느린 수렴 과정이 진행됨
• 학습률이 너무 큰 경우 수렴과정 가운데 너무 빈번한게 최솟값 주변만 맴돌게 됨

2. 학습률 조정의 어려움

• 학습률은 훈련 과정에서 조절되며 이전에 정의된 경우에 따라 줄어들기도하고 각 배치마다 달라지게 됨
• 데이터 셋의 특성에 따라 조절하고 정의하기가 어려움

3. 모든 업데이트마다 같은 학습률을 사용함

• 우리 데이터가 분산되어 있고 특징들이 매우 다른 경우 매 배치마다 같은 학습률을 사용함
• 흔하지 않은 특성에 대해 너무 자주 업데이트가 발생할 수 있음

4. SGD에서 안장점에서 탈출할 우려가 있음

• 지역 최솟값에 갇히는 것을 피하는 과정에서 안장점에서 오류가 발생함
• 한 차원이 위로 기울어지고 다른 차원이 아래로 기울어지는 안장점은 동일한 오류로 둘러싸여 있어 SGD가 어려움을 겪음
• Gradient가 모든 차원에서 0에 가까워 탈출함

경사하강법 최적화 알고리즘

1. Momentum

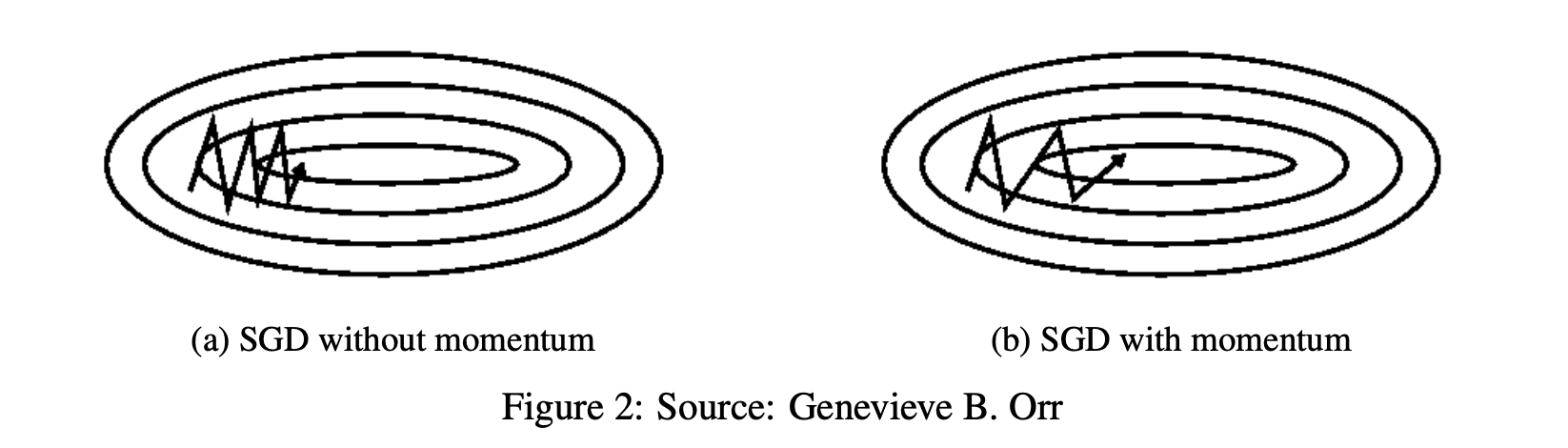
• 가파른 지역에 대하여 더 가파르게 탐색
• 감마로 같은 방향을 가리키는 차원에 대해 증가하고 경사가 방향을 변경하는 차원에 대한 업데이트를 줄임 과한 경우를 줄임
• γ는 0.9나 비슷한 값으로 세팅하는 것을 권장함

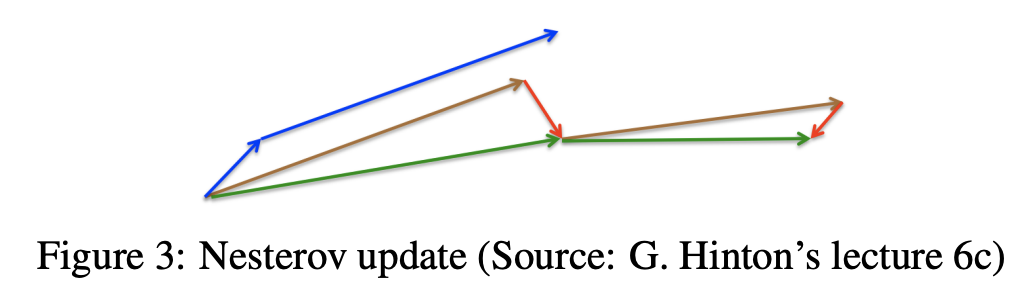
2. Neserov accelerated gradient

• NAG는 이전 축적된 경사로 움직이고(모멘텀으로 이동하고) 그 자리에서 그레디언트를 다시 계산
• γ는 모멘텀과 비슷하게 대략적으로 0.9 주변으로 설정

3. Adagrad

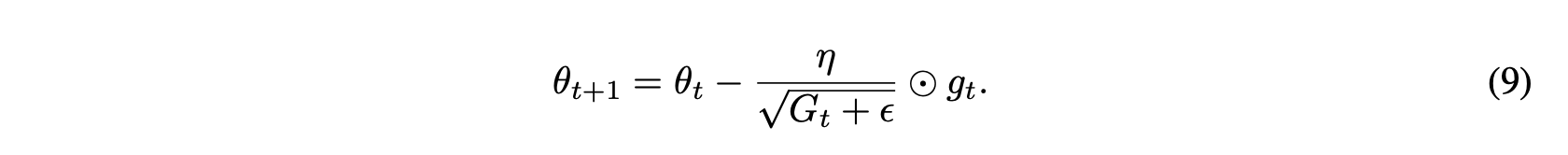
• 빈번하지 않은 파라미터에 대해 큰 업데이트를 하고 빈번한 파라미터에 대해 더 작은 업데이트를 진행함
• 매 단계 t에서 모든 파라미터에 대해 다른 학습률을 사용함
• 분모에 제곱된 경사가 누적됨
• 2차 행렬에 과거 그레디언트를 누적한 값을 저장해 사용함
• Adagrad는 분산된 데이터를 처리하는데 있음

3-1. Adadelta

• 과거 제곱 경사를 모두 누적하는 대신 누적된 과거 경사의 창을 고정된 크기 w로 제한
• 경사 합계는 모든 과거 경사 제곱의 감쇠 평균으로 재귀적으로 정의

3-2. RMSprop

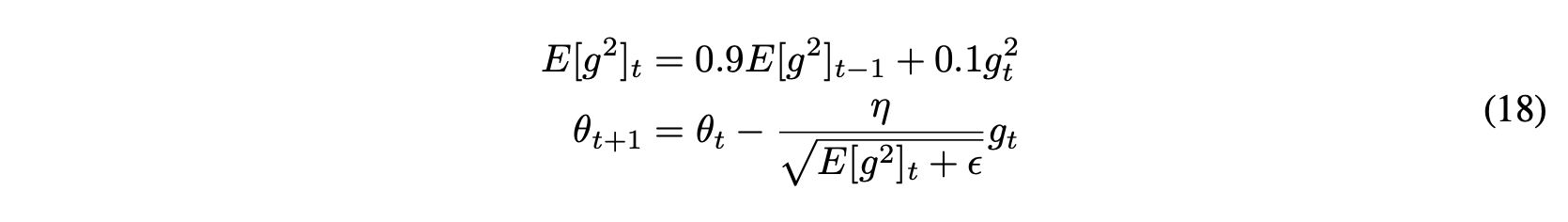
• 학습 속도가 급격히 감소하는 문제를 해결하기 위해 독립적으로 개발
• 학습률을 지수적으로 감소하는 평균 제곱 기울기로 나눔

4. Adam(Adaptive Moment Estimation)

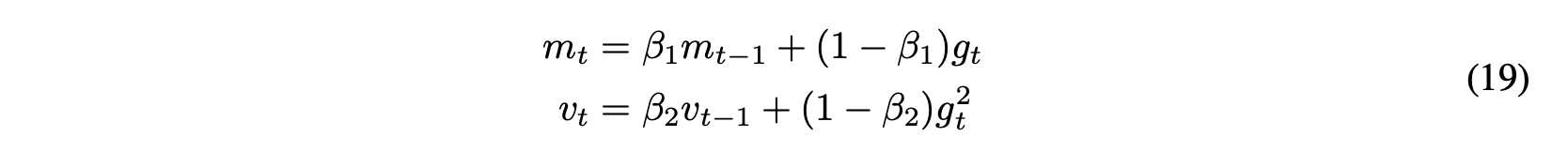
• mt는 처음 모먼트의 측정 값(평균)이고 vt는 두번째 모먼트인 분산을 의미한다. 처음에는 0으로 설정이 되어 있음
• 각 매개 변수에 대한 적응 학습률을 계산하는 또 다른 방법
• Moment와 유사하게 과거 경사를 지속적으로 감소하는 평균을 유지

4-1. AdaMax

• L2 norm -> Lp norm
• 이 말은 기존 l2 norm 계산 과정을 각 모든 상황에서 업데이트를 하여 새로 정의한다는 의미

4-2. Nadam

• Adam은 RMSprop과 momentum을 결합한 요소이고 여기서 더 발전해 Nestrov 개념을 더 추가한 것이 Nadam이다.

최종 정리

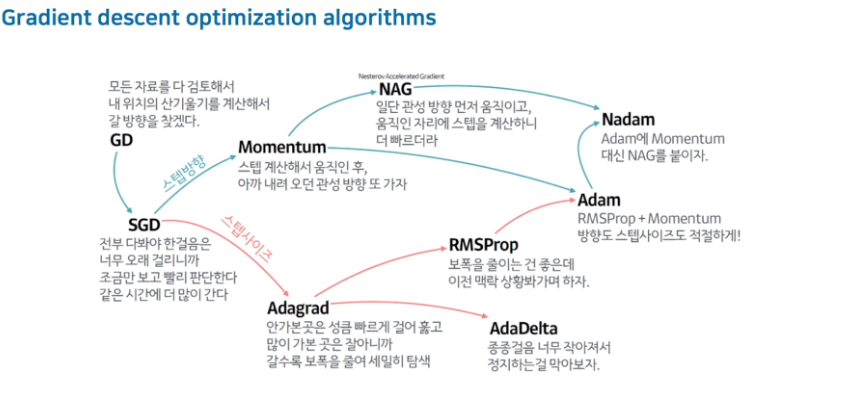
• 논문에는 너무나도 다양한 수식들이 존재해서 직접 블로그에 작성하기가 어렵지만 그래도 기본적인 Gradient Algorithm의 흐름은 위 그림을 보면서 학습하면 될 것같다.