Layer란?
- 사전적의미
하나의 물체가 여러 개의 논리적인 객체들로 구성되어 있는 경우, 이런한 각각의 객체를 하나의 레이어라 한다.
신경망이라는 물체를 구성하는 여러 개의 논리적인 레이어들을 이해하고 레이어의 Weight(가중치)를 알아내는 것이 최종적인 목표이다.
1.Linear Layer
Linear Layer는 선형 변환을 활용해 데이터를 특정 차원으로 변환하는 기능을 한다.
예를 들어 100차원의 데이터를 300차원으로 변환한다면 데이터를 더 풍부하게 표현하는 효과가 있고 반대로 10차원의 데이터로 변환한다면 데이터를 집약시키는 효과가 있다.
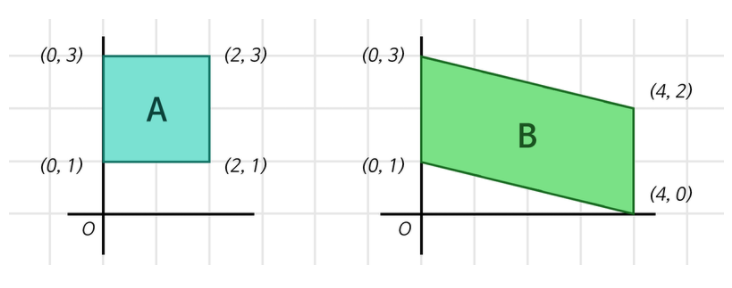
위와 같이 두 사각형은 모두 2차원의 점 4개로 표현 가능하고 (4, 2) : (점의 개수, 차원) 행렬 형태의 데이터로 표현이 가능하다.
이를 하나의 정수로 표현하고자 한다면 2단계 과정을 거쳐서 하나의 점으로 표현이 가능하다.
1단계 : (4, 2) x (2, 1)(=(입력 차원, 출력 차원)) = (4, ) ---> 🤔(4, 1)에서 1이 생략 된건가...?
2단계 : (4, ) x (4, 1) = (1, )
위의 단계를 코드로 표현
import tensorflow as tf batch_size = 64 boxes = tf.zeros((batch_size, 4, 2)) # Tensorflow는 Batch를 기반으로 동작하기에, # 우리는 사각형 2개 세트를 batch_size개만큼 # 만든 후 처리를 하게 됩니다. print("1단계 연산 준비:", boxes.shape) first_linear = tf.keras.layers.Dense(units=1, use_bias=False) # units은 출력 차원 수를 의미합니다. # Weight 행렬 속 실수를 인간의 뇌 속 하나의 뉴런 '유닛' 취급을 하는 거죠! first_out = first_linear(boxes) first_out = tf.squeeze(first_out, axis=-1) # (4, 1)을 (4,)로 변환해줍니다. # (불필요한 차원 축소) print("1단계 연산 결과:", first_out.shape) print("1단계 Linear Layer의 Weight 형태:", first_linear.weights[0].shape) print("\n2단계 연산 준비:", first_out.shape) second_linear = tf.keras.layers.Dense(units=1, use_bias=False) second_out = second_linear(first_out) second_out = tf.squeeze(second_out, axis=-1) print("2단계 연산 결과:", second_out.shape) print("2단계 Linear Layer의 Weight 형태:", second_linear.weights[0].shape)
📄Output

코드의 시각화
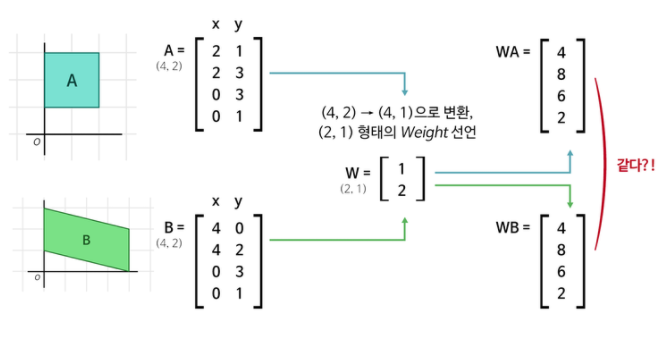
위 그림을 따라가면 두 사각형에 대해 1단계를 거치고 난 결과가 동일해 진다. 이렇게 되면 <단계2>에서 입력이 동일해져 두 번째 (4, 1)Weight를 거치는 거의 의미가 없어진다. 이것을 해결하기 위해 Parameter(Weight의 모든 요소)를 늘려주기 위한 단계를 하나 추가한다.
1단계 : (4, 2) x (2, 3) = (4, 3) ---> New!!
2단계 : (4, 3) x (3, 1) = (4, )
3단계 : (4, ) x (4, 1) = (1, )
개선된 코드
import tensorflow as tf batch_size = 64 boxes = tf.zeros((batch_size, 4, 2)) print("1단계 연산 준비:", boxes.shape) first_linear = tf.keras.layers.Dense(units=3, use_bias=False) first_out = first_linear(boxes) print("1단계 연산 결과:", first_out.shape) print("1단계 Linear Layer의 Weight 형태:", first_linear.weights[0].shape) print("\n2단계 연산 준비:", first_out.shape) second_linear = tf.keras.layers.Dense(units=1, use_bias=False) second_out = second_linear(first_out) second_out = tf.squeeze(second_out, axis=-1) print("2단계 연산 결과:", second_out.shape) print("2단계 Linear Layer의 Weight 형태:", second_linear.weights[0].shape) print("\n3단계 연산 준비:", second_out.shape) third_linear = tf.keras.layers.Dense(units=1, use_bias=False) third_out = third_linear(second_out) third_out = tf.squeeze(third_out, axis=-1) print("3단계 연산 결과:", third_out.shape) print("3단계 Linear Layer의 Weight 형태:", third_linear.weights[0].shape) total_params = \ first_linear.count_params() + \ second_linear.count_params() + \ third_linear.count_params() print("총 Parameters:", total_params)
📄Output
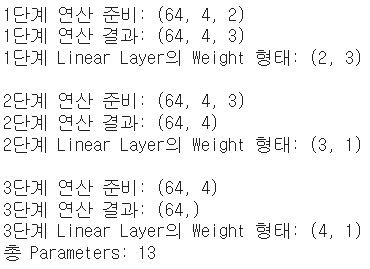
개선된 코드의 시각화
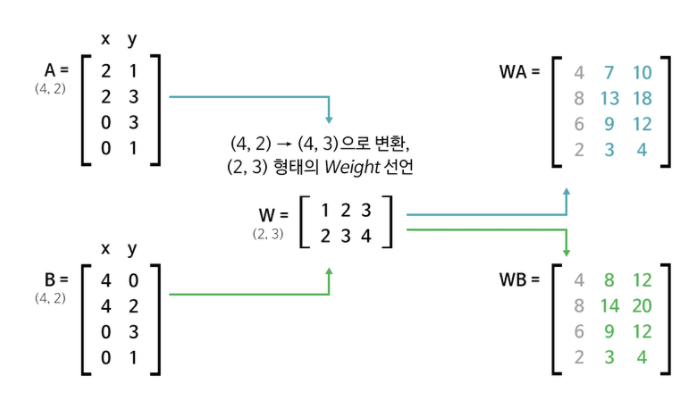
이러한 결과를 보고 "Parameter를 늘리면 항상 좋은 값을 가지는가?"에 대한 의문이 있을 수 있지만 결론적으로 말하자면 False입니다. 너무 많은 Parameter는 과적합(Overfitting : 문제만 보고 정답을 외워서 답하는 경우)을 야기하니다.
2. Convolution Layer
이미지에서 특징(Feature)를 뽑아내기 필터를 사용하고 뽑아낸 특징을 사용해 분류(Classification)한다.
예를 들어 FHD(1920 x 1080)의 컬러 이미지(3개의 채널)이 있다고 할 때 기존의 Linear Layer를 사용하면 대략 620만 개의 Parameter가 생선된다. 이는 모든 픽셀을 한 줄씩 살펴보아야하고 계산이 매우 비효율적이기 때문에 문제해결을 위해 고안된 것이 Convolution Layer이고 Convolution 연산은 딥러닝 이외에도 많이 사용되는 개념이다.
필터를 통해 이미지가 겹쳐지는 부분의 Convolution 연산
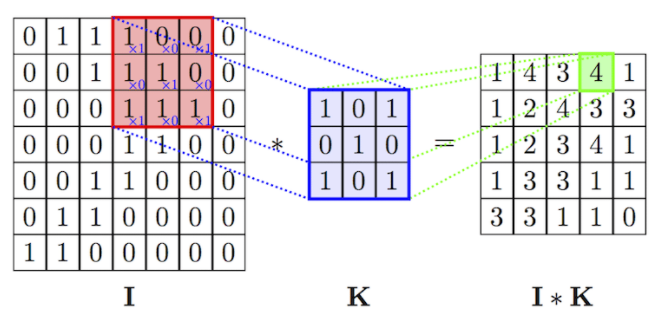
필터가 이미지를 훓으며 각 픽셀을 곱하여 더하는 Convolution 연산
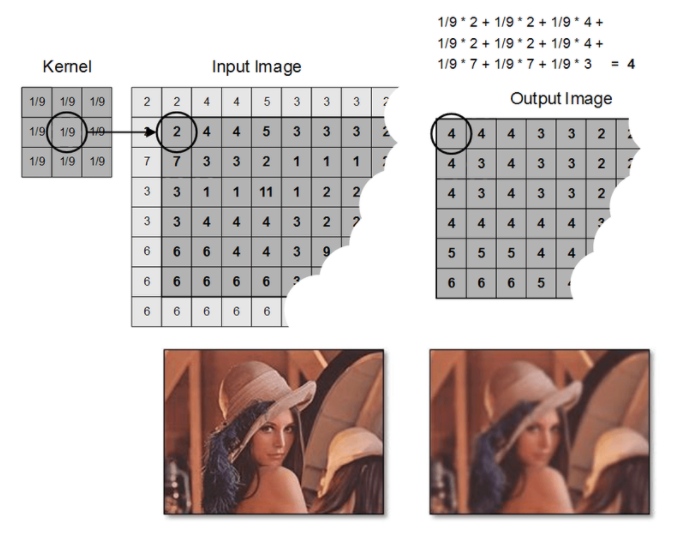
위와 같이 한 칸씩 훓으며 Convolution 연산을 수행할 수 있지만 여러 칸씩 이동하며 훓을 수 도 있는데 이를 결정하는 값을 Stride 라고한다.
하지만 Convolution 연산은 입력의 형태를 변형시킨다는 아주 사소한 문제가 있는데 예를 들어 [1, 2, 3, 4, 5]라는 데이터를 [1, 0, -1]이라는 필터(Stride = 1)로 훓게되면 3번의 연산밖에 진행하지 못한다. 입력은 (5, )이지만 출력은 (3, )이 된다. 이를 방지하기 위해 Padding이라는 개념을 사용하며 입력의 테두리에 "0(zero)"을 추가하여 [0, 1, 2, 3, 4, 5, 0]의 형태로 변환함으로서 출력의 형태를 맞춰준다.
Convolution Layer의 코드
- 필터 정의
16개, 5 x 5, Stride = 5
( = 1200개의 Parameter)1단계 : (1920, 1080, 3) x [3 x 16 x 5 x 5 Weight & Stride 5] = (384, 216, 16)
2단계 : (384, 216, 16) → (384 x 216 x 16, )
3단계 : (1327104, ) x [1327104 x 1 Weight] = (1, )import tensorflow as tf batch_size = 64 pic = tf.zeros((batch_size, 1920, 1080, 3)) print("입력 이미지 데이터:", pic.shape) conv_layer = tf.keras.layers.Conv2D(filters=16, kernel_size=(5, 5), strides=5, use_bias=False) conv_out = conv_layer(pic) print("\nConvolution 결과:", conv_out.shape) print("Convolution Layer의 Parameter 수:", conv_layer.count_params()) flatten_out = tf.keras.layers.Flatten()(conv_out) print("\n1차원으로 펼친 데이터:", flatten_out.shape) linear_layer = tf.keras.layers.Dense(units=1, use_bias=False) linear_out = linear_layer(flatten_out) print("\nLinear 결과:", linear_out.shape) print("Linear Layer의 Parameter 수:", linear_layer.count_params())
📄Output

3. Pooling Layer
Convolution Layer를 통해 Linear Layer보다 훨씬 적은 수의 Parameter로 이미지의 특징을 추출할 수 있었다. 하지만 Convolution Layer만으ㅏ로는 객체를 판별해 내기에 문제가 있다.
문제 1. 5 x 5라는 필터 사이즈는 Object Detection을 위한 유의미한 정보를 담아내기에는 너무 작은 크기이다.
문제 2. 이미 Stride를 5로 주고 있었기 때문에 Parameter를 줄이는데에는 효과적이지만 찾고자 하는 객체가 필터 경계선에 걸려서 인식하지 못할 우려가 있다.
위의 문제를 해결하기 위해 필터의 크기를 크게하게 된다면 극단적인 경우 필터의 크기가 이미지의 크기와 동일해지고 그것은 Linear Layer와 같아지게 된다.
그리고 필터의 크기를 키우면 Parameter의 크기와 연산량이 커지므로 정확도(Accuracy)도 떨어진다.
결과적으로 우리가 해야할 것은 필터의 크기를 조절하는 것이 아닌 수용영역(Receptive Field)이라는 개념을 사용하는 것이다.
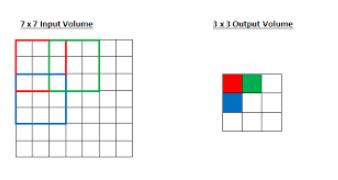
위의 그림은 7 x 7 크기의 이미지에 3 x 3의 필터로 Convolution Layer를 한 번 통과한 후 Output의 빨간색 포인트는 원본 이미지의 좌상단 3 x 3 만큼의 입력만을 수용하고 결과적으로 수용영역의 크기는 필터의 크기와 같아진다.
CNN(Convolutional Neural Network)에서는 흔히 Max Pooling Layer가 뒤따른다.
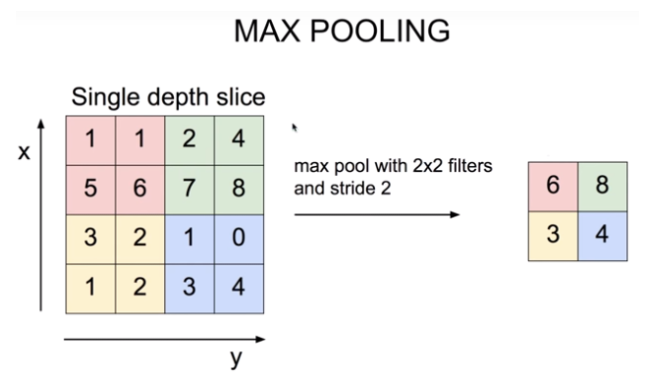
Translational Invariance Effect
이미지는 약간의 상하좌우 시프트가 생긴다고 해도 내용상 동일한 특지이 있는데 Max Pooling을 통해 인접한 영역 중 가장 특징이 두드러진 영역 하나를 뽑는 것은 오히려 약간의 시프트 효과에도 불구하고 동일한 특징을 안정적으로 잡아낼 수 있는 긍정적 효과가 있어서 오히려 객체 위치에 대해 과적합을 방지하고 안정적이 특징 추출을 할 수 있다.
Non-Linear Function과 동일한 Feature Extraction Effect
Relu와 같은 Non-Linear Function도 마찬가지로 많은 하위 Layer의 연산 결과를 무시하는 효과를 방생시키지만 그 결과 중요한 특징만을 상위 Layer로 추출해서 올려줌으로써 결과적으로 분류기의 성능을 증진시키는 효과를 가진다.
Receptive Field Maximization Effect
Max Pooling이 엇이도 Receptive Field를 크게 하려면 Convolutional Layer를 아주 많이 쌓아야 한다. 그 결과 큰 파라미터 크기로 인한 과적합, 연산량 증가, 특이점 소실 등의 문제를 감수해야한다. 이 문제를 해결하기 위한 두 가지 방법 중 하나가 Max Pooling이고 나머지 하나가 Dilated Convolution 이다.
4. Deconvolution Layer
Deconvolution Layer는 Convolution의 결과를 역재생해서 원본 이미지와 최대한 유사한 저보를 복원해 내는 것으로 Auto Encoder라는 모델을 사용하여 복원한다.
Auto Encoder
패키지 임포트 및 MNIST 데이터셋 로딩
AutoEncoder 모델 구성
AutoEncoder 모델 훈련
AutoEncoder Reconstruction Testimport numpy as np from tensorflow.keras.layers import Input, Dense, Conv2D, MaxPooling2D, UpSampling2D from tensorflow.keras.models import Model from tensorflow.keras.datasets import mnist import json import matplotlib.pyplot as plt #for plotting # MNIST 데이터 로딩 (x_train, _), (x_test, _) = mnist.load_data() # y_train, y_test는 사용하지 않습니다. x_train = np.expand_dims(x_train, axis=3) x_test = np.expand_dims(x_test, axis=3) x_train = x_train.astype('float32') / 255. x_test = x_test.astype('float32') / 255. # AutoEncoder 모델 구성 - Input 부분 input_shape = x_train.shape[1:] input_img = Input(shape=input_shape) # AutoEncoder 모델 구성 - Encoder 부분 encode_conv_layer_1 = Conv2D(16, (3, 3), activation='relu', padding='same') encode_pool_layer_1 = MaxPooling2D((2, 2), padding='same') encode_conv_layer_2 = Conv2D(8, (3, 3), activation='relu', padding='same') encode_pool_layer_2 = MaxPooling2D((2, 2), padding='same') encode_conv_layer_3 = Conv2D(4, (3, 3), activation='relu', padding='same') encode_pool_layer_3 = MaxPooling2D((2, 2), padding='same') encoded = encode_conv_layer_1(input_img) encoded = encode_pool_layer_1(encoded) encoded = encode_conv_layer_2(encoded) encoded = encode_pool_layer_2(encoded) encoded = encode_conv_layer_3(encoded) encoded = encode_pool_layer_3(encoded) # AutoEncoder 모델 구성 - Decoder 부분 decode_conv_layer_1 = Conv2D(4, (3, 3), activation='relu', padding='same') decode_upsample_layer_1 = UpSampling2D((2, 2)) decode_conv_layer_2 = Conv2D(8, (3, 3), activation='relu', padding='same') decode_upsample_layer_2 = UpSampling2D((2, 2)) decode_conv_layer_3 = Conv2D(16, (3, 3), activation='relu') decode_upsample_layer_3 = UpSampling2D((2, 2)) decode_conv_layer_4 = Conv2D(1, (3, 3), activation='sigmoid', padding='same') decoded = decode_conv_layer_1(encoded) # Decoder는 Encoder의 출력을 입력으로 받습니다. decoded = decode_upsample_layer_1(decoded) decoded = decode_conv_layer_2(decoded) decoded = decode_upsample_layer_2(decoded) decoded = decode_conv_layer_3(decoded) decoded = decode_upsample_layer_3(decoded) decoded = decode_conv_layer_4(decoded) # AutoEncoder 모델 정의 autoencoder = Model(input_img, decoded) autoencoder.summary() autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy') autoencoder.fit(x_train, x_train, epochs=50, batch_size=256, shuffle=True, validation_data=(x_test, x_test)) x_test_10 = x_test[:10] # 테스트 데이터셋에서 10개만 골라서 x_test_hat = autoencoder.predict(x_test_10) # AutoEncoder 모델의 이미지 복원생성 x_test_imgs = x_test_10.reshape(-1, 28, 28) x_test_hat_imgs = x_test_hat.reshape(-1, 28, 28) plt.figure(figsize=(12,5)) # 이미지 사이즈 지정 for i in range(10): # 원본이미지 출력 plt.subplot(2, 10, i+1) plt.imshow(x_test_imgs[i]) # 생성된 이미지 출력 plt.subplot(2, 10, i+11) plt.imshow(x_test_hat_imgs[i])
📄Output


