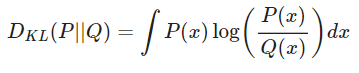정보 이론(Information Theory)이란?

추상적인 정보라는 개념을 정량화하고 정보의 저장과 통신을 연구하는 분야이다.

1. 정보량(Information Content)

정보를 정량적으로 표현하기 위한 세 가지 조건

1. 일어날 가능성이 높은 사건은 정보량이 낮고 반드시 일어나는 사건에는 정보가 없는 것과 같다.
   (예시) 파란색 공 999개와 빨간색 공 1개가 들어 있는 주머니가 있다고 가정하고 공을 하나씩 뽑으면 처음에 뽑은 파란색 공은 정보량이 높지만 점차 정보량이 낮아지고 파란색 공을 뽑을 확률이 1에 가까워 질수록 큰 의미를 주지 못한다. 하지만 중간에 빨간색 공을 뽑는다면 이는 높은 정보량을 가진 사건이고 파란색 공의 수가 많을수록(빨간색 공을 뽑을 확률이 낮을수록) 빨간색 공을 뽑는 사건의 정보량은 높아진다.

2. 일어날 가능성이 낮은 사건은 정보량이 높다.

3. 두개의 독립적인 사건이 있을 때 전체 정보량은 각각의 정보량을 더한 것과 같다.

사건 $x$가 일어날 확률을 $P(X = x)$라고 할 때 사건의 정보량(Information Content)은 $I(x) = -log_bP(x)$로 정의 된다.

💡Tip $b$에는 주로 2, $e$(자연로그), 10과 같은 값이 사용되며 $b = 2$인 경우 정보량은 정보를 나타내기 위해 필요한 bit의 개수와 같다.

아래의 그래프는 $b = e$일 때 $P(x)$의 값에 대한 $-logP(x)$의 그래프이다.

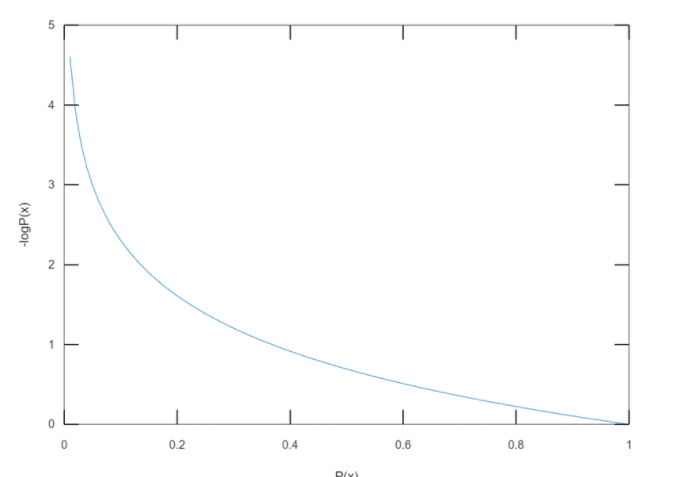
파란색 공 $n$개와 빨간색 공 1개가 있을 때 빨간색 공을 뽑는 사건의 정보량을 계산하는 코드

• 빨간색 공이 뽑힐 대 까지 공을 꺼내는 시뮬레이션이 반복되며 전체 공의 개수가 많을수록 1개 있는 빨간색 공이 뽑힐 확률은 작아지고 평균적으로 계사되는 정보량이 커진다.

import numpy as np
import math
import random

# 주머니 속에 들어있는 공의 개수입니다. 숫자를 바꾸면서 실험해보세요!
total = 1000

#---------------#

count = 1   # 실험이 끝날 때까지 꺼낸 공의 개수

# 1부터 total까지의 정수 중에서 하나를 뽑고 total과 같으면 실험 종료
# total=1000인 경우 1~999: blue / 1000: red
while True:
    sample = random.randrange(1,total+1)
    if sample == total:
        break
    count += 1

print('number of blue samples: '+str(count-1))
print('information content: '+str(-math.log(1/count)))

📄Output

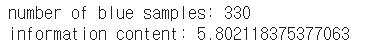
2. Entropy

정보량이 한 가지 사건에 대한 값이라면 특정 확률분포를 따르는 사건들의 정보량 기댓값을 Entropy라고 한다.

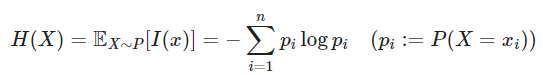
Entropy는 이산확률 변수 $X$가 $x_1, x_2, ..., x_n$중 하나의 값을 가진다고 가정하고 각각의 경우의 수가 가지는 정보량에 확률을 곱한 후 그 값을 모두 더한 값으로 식으로 표현하면 위의 식과 같이 표현이 가능하다.

For Discrete Random Variables

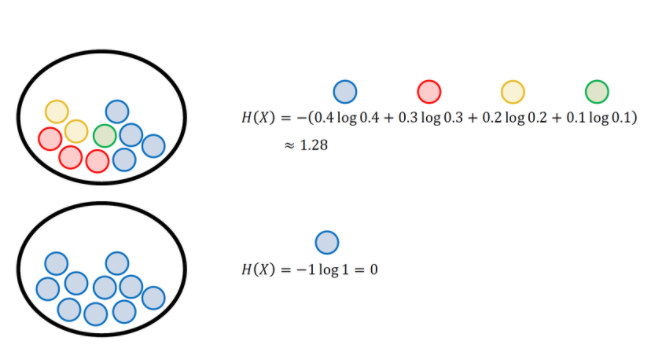
위 그림은 여러 색의 공이 들어 있는 주머니에서 공을 꺼낼 때 각각의 Entropy값을 계산한 예제이다. 위쪽 주머니에는 4가지 색깔의 공이 들어있고 특정한 색깔의 공이 뽑힐 확률이 각각 0.4, 0.3, 0.2, 0.1이므로 Entropy는 약 1.28이다.

아래쪽 주머니에는 파란색 공만 들어있고 파란색 공이 뽑힐 확률이 1이므로 Entropy는 $0(= -1log1)$이 된다.

여러 색깔의 공이 들어있을 때(모든 공의 색이 다를 때) Entropy가 높고(약 $2.3$) 같은 색깔의 공이 많이 있을 때(모든 공의 색이 같을 때) Entropy가 가장 낮다($0$).

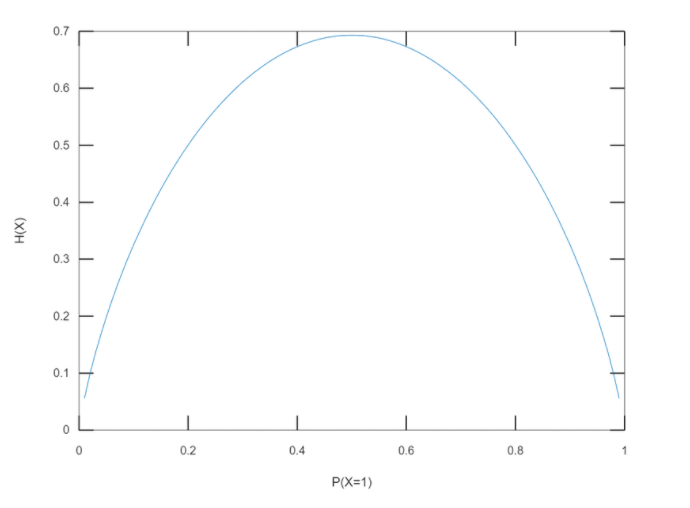
위의 그림은 동전을 던져서 앞면이 나올 확률에 따른 Entropy를 나타낸 것인데 앞면이 나올 확률과 뒷면이 나올 확률이 $0.5$로 동일하기 때문에 결과를 예측을 하기 어려워 값이 최대가 되는 모습을 볼 수 있다.

3. Kullback Leibler Divergence

머신러닝의 목표는 새로운 입력 데이터가 들어와도 예측이 잘 되도록 모델의 확률 분포를 데이터의 실제 확률 분포에 가깝게 만드는 것이다. 머신 러닝 모델은 크게 두 가지가 있는데 하나는 우선 결정 모델(Discriminative Model)은 데이터의 실제 분포를 모델링 하지 않고 결정 경계(Decision Boundary)만을 학습한다. 예를 들면 모델의 결과값이 0보다 작을 경우 데이터를 1번 클래스로 분류하고 0보다 클 경우 2번 클래스로 분류하는 방식이다. 그리고 또하나의 모델은 생성 모델(Generative Model)이다. 생성 모델은 데이터와 모델로부터 도출할 수 있는 여러 확률 분포와 베이즈 이론을 이용해서 데이터의 실제 분포를 간접적으로 모델링 한다. 그렇기 때문에 생성 모델을 학습시킬 때는 두 확률 분포의 차이를 나타내는 지표가 필요한데 대표적으로 사용하는 것이 Kullback Leibler Divergence이다.

1. 데이터가 따르는 실제 확률 분포를 $P(x)$

2. 모델이 나타내는 확률 분포를 $Q(x)$

두 확률 분포의 Kullback Leibler Divergence는 $P(x)$를 기준으로 계산된 $Q(x)$의 평균 정보량과 $P(x)$를 기준으로 계산된 $P(x)$의 평균 정보량의 차이로 정의 할 수 있다.

💡Tip 연속 확률 변수의 경우

Kullback Leibler Divergence는 두 확률 분포의 차이를 나타내는 값이기 때문에 거리 함수와 비슷한 성질을 가지고 있지만 Kullback Leibler Divergence의 식에는 기준이 되는 확률 분포가 존재하기 때문에 $D_{KL}(P∣∣Q)$와 $D_{KL}(Q∣∣P)$의 값은 같지 않다.

Kullback Leibler Divergence의 특성

1. $D_{KL}(P∣∣Q) ≥ 0$

2. $D_{KL}(P∣∣Q) = 0$ if and olny if $P = Q$

3. non-symmetric : $D_{KL}(P∣∣Q) ≠ D_{KL}(Q∣∣P)$

4. Cross Entropy Loss

머신러닝에서 모델이 나타내는 확률 분포와 데이터가 따르는 실제 확률 분포 사이의 차이를 나타내는 함수를 손실 함수 (Loss Function)라고 한다. 모델의 확률 분포는 파라미터에 따라 달라지기 때문에 손실 함수 역시 파라미터에 의해 결정된다.

데이터가 연속적인 값을 가지는 회귀 문제와는 다르게 이산적인 값을 가지는 분류 문제에서는 모델의 출력 결과가 로지스틱 함수로 표현된다. 분류 클래스가 2개인 로지스틱 함수를 클래스가 $n$개일 때로 확장한 것이 딥러닝에서도 자수 사용되는 Softmax Function이다. 그리고 Cross Entropy Loss 또한 손실 함수의 한 종류이고 아래와 같이 표현이 가능하다.

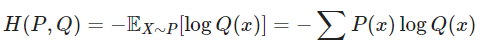
분류 문제에서 데이터의 라벨은 One-Hot Encoding을 통해 표현된다. 클래스의 종류가 $N$가지이고 특정 데이터가 $n$번째 클래스에 속할 때 $n$번째 원소만 1이고 나머지는 $0$으로 채운 $N$차원 벡터로 놓는 것이다.

입력 데이터의 특성(Feature)값이 모델을 통과하면 출력 레이어의 Softmax Function에 의해서 각각의 클래스에 속할 확률이 계산되는데 이 확률 값들이 모델이 추정한 확률 분포 $Q(x)$를 구성하는 값이 된다. 3개의 클래서 $c1, c2, c3$가 존재하는 불류 문제에서 어떤 데이터의 출력값은 아래와 같다고 가정하면

이 결과는 곧 다음 식을 나타낸다.

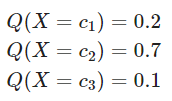
데이터가 실제로 2번 클래스에 속할 경우 데이터의 실제 확률 분포는 One-Hot Encoding과 같은 $[0, 1, 0]$이고 데이터가 2번 클래스에 포함된다는 사실이 이미 확실하게 아렬 졌기 때문에 확률 분포가 아래와 같이 계산된다.

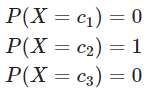
이것을 Cross Entropy를 사용하여 계산할 수 있다.

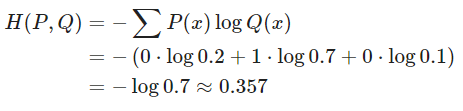
분류 문제에서는 데이터의 확률 분포가 위와 같이 One-Hot Vector로 표현되기 때문에 $P(x)$와 $Q(x)$분포가 랜덤하게 생성 되었을 때 $P(x)$를 변형시키면서 Cross Entropy를 계산할 수 있다.

Cross Entropy 에시 코드

import numpy as np
import random

# generate random output
#-----------------#
# can be modified
class_num = 4
#-----------------#
q_vector = []
total = 1

for i in range(class_num-1):
    q = random.uniform(0,total)
    q_vector.append(round(q,3))
    total = total - q

q_vector.append(total)
softmax_output = np.array(q_vector)

print(softmax_output)

#-----------------#
# can be modified
class_index = 1
#-----------------#

p_vector = np.zeros(class_num)
p_vector[class_index-1] = 1

cross_entropy = -np.sum(np.multiply(p_vector, np.log(softmax_output)))

print('model prediction: '+str(softmax_output))
print('data label: '+str(p_vector))
print('cross entropy: '+str(round(cross_entropy,4)))

📄Output