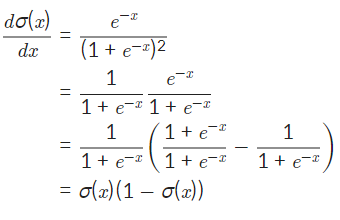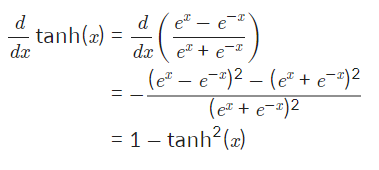활성화 함수(Activation Function)란?
특정 행동을 함 → 특정 조건을 만족 → 함수 활성화와 같은 흐름을 가지고 동작하며 신경망 속의 퍼셉트론 혹은 노드도 특정 조건이 만족하면 활성화 되도록 디자인되어 있다.
예를들어 ReLU의 경우 입력값이 음수라면 0을 출력하고 입력값이 0이상이라면 입력값 그대로를 출력하도록 디자인되어 있는데 이를 활성화 또는 비활성화로 표현 하려면 우선 활성화 되는 기준을 정하고 출력값이 0보다 큰 경우를 활성화되었다고 정의한다.
💡Tip 활성화 함수는 모델의 표현력을 왜 향상시켜줄까?
어떤 모델이 이라는 2개의 파라미터로 이루어진 이라고 한다면 이 모델은 등으로 표현되는 데이터를 학습할 수 없다. 그 이유는 w1, b1값을 아무리 바꿔도 와 같은 함수는 절대 표현할 수 없기 때문이다.
이를 수학적으로 말하면 선형 함수로는 비선형 함수를 표현할 수 없다라고 말한다.
하지만 딥러닝 모델의 들은 입력값 와 선형관계이다. 그리고 아무리 많은 Layer들을 겹쳐도 그 결과는 선형관계인데 곡선처럼 직선으로는 근사시킬 수 없는 비선형 데이터를 표현하려면 딥러닝 모델도 비선형성을 지니고 있어야 한다. 이때 쓰이는 것이 활성화 함수이고 활성화 함수를 Layer 사이사이에 넣어줌으로써 모델이 비선형 데이터도 표현할 수 있게 되었다.
1. 퍼셉트론(Perceptron) : 활성화 함수는 어디서 기인되었는가?
딥러닝 모델은 보통 여러 개의 층으로 이루어져 있으며 그중에 하나의 층을 가져와 다시 쪼갠다면 보통 Node라고 불리는 것으로 쪼개지는데 이것이 바로 Perceptron이다.
💡Tip 퍼셉트론을 쌓으면 단층 퍼셉트론이 되고 이 단층 퍼셉트론을 쌓으면 다층 퍼셉트론이 된다.
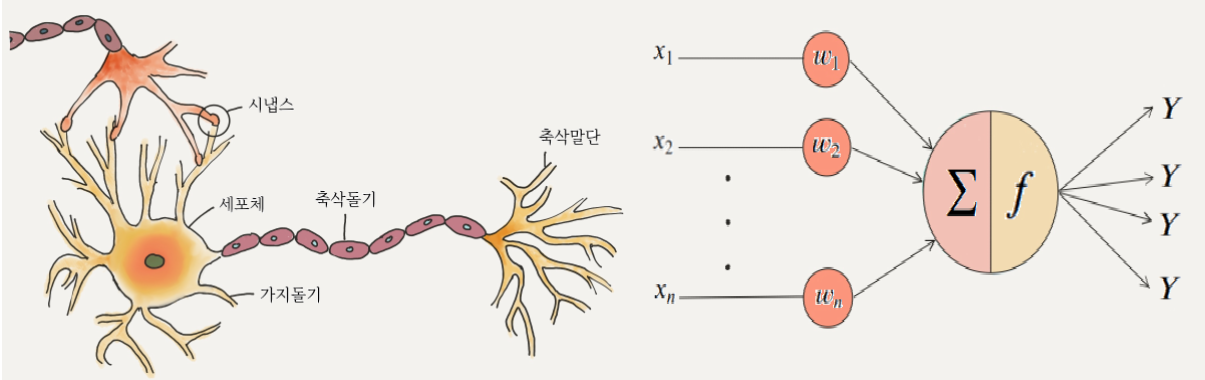
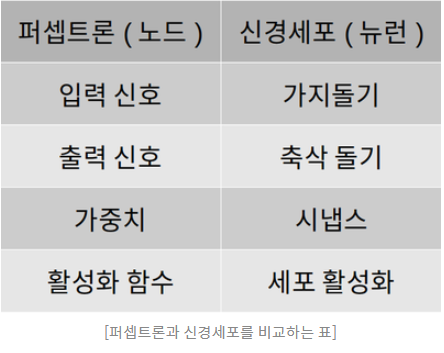
퍼셉트론은 신경세포와 그 구조가 동일하고 퍼셉트론의 입력은 신경세포에서 가지돌기에 해당하고 각 입력 항에 곱해지는 가중치는 시냅스의 발달 정도에 해당하며 값들은 각 가지돌기에서 시냅스를 거쳐서 오는 신호들에 해당된다. 세포체에서 이 신호들을 합쳐()지고 합쳐진 신호는 세포체에서 신호를 처리하는 방식과 비슷하게 적절한 활성화 함수를 거쳐 출력이 결정된다.
2. 선형 변환(Linear Transformation)
-
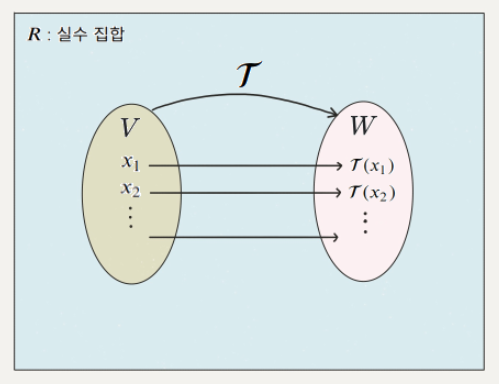
선형 변환의 정의
와 가 어떤 벡터를 그릴 수 있는 공간(좌표평면)이고 둘 모두 실수집합(Field)상에 있다고 가정하면 함수 의 식을 만족한다는 의미이다.
-
선형 변환의 성질

3. 비선형(Non-Linear)
-
왜 비선형 함수를 쓰는가?
결론적으로 말하면 딥러닝 모델의 표현력을 향상시키기 위해서 사용한다. -
선형 활성화 함수를 사용하면 왜 표현력이 떨어지는가?
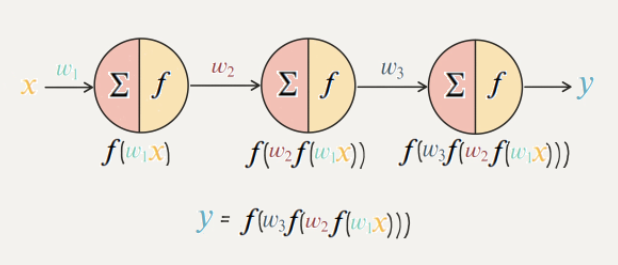
위의 그림과 같은 3개의 퍼셉트론으로 구성된 모델이 있다고 가정하고 입력앖 가 모델을 거치면 출력값 가 된고 수식으로 표현하면 와 같이 표현할 수 있다.
는 가중치이며 편향값 는 편의를 위해 0으로 설정한다.이때 가 선형이라면 선형 함수의 정의에 의해 로 쓸수 있기 때문에 을 아래와 같이 합칠 수 있다.
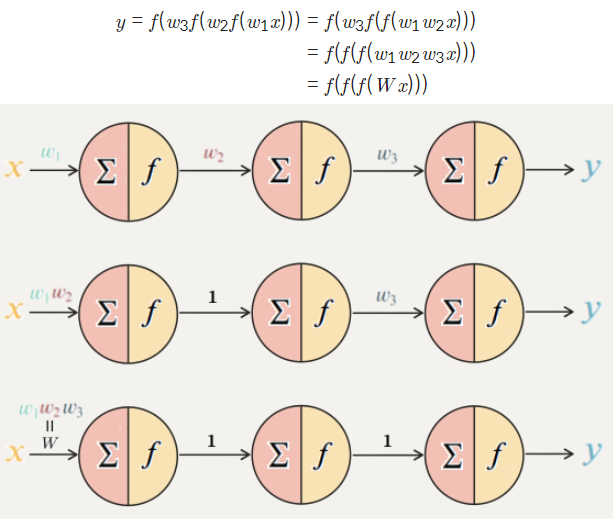
이것의 의미는 가중치의 업데이트가 셋 전부에서 일어날 필요가 없다는 뜻으로 의 가중치를 모두 1로 초기화 하고 모델을 훈련시켰을 때 최종적으로 훈련된 모델의 가중치들이 라고 할 수 있다. 이것을 식으로 하면 와 같이 표현할 수 있고 다시 함수 가 선형인 것을 이용해 식을 으로 바꿔줄 수 있다.여기서 은 사실상 의 가중치를 모두 1로 초기화하고 모델을 훈련시켰을 때 와 은 업데이트되지 않게 고정시키고 만 업데이트한 것과 같다.
즉 나 의 가중치가 어떻게 변하는지와 상관없이 만 잘 업데이트되면 결과는 같다는 뜻이다.
을 로 표현하면 이 또한 선형이다.
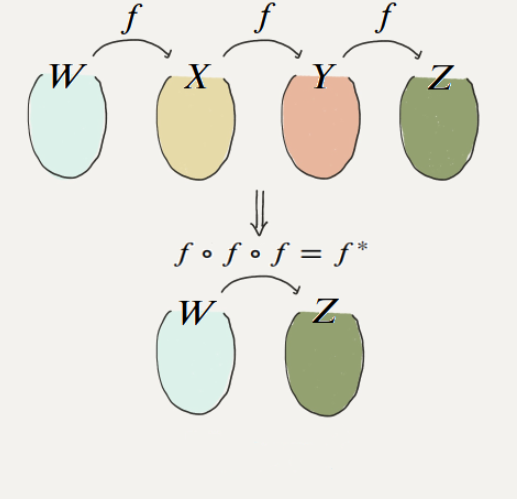
결론적으로 선형 활성화 함수를 사용한다면 노드의 개수를 아무리 많이 붙여도 결국 하나의 노드를 사용하는 것과 차이가 없기 때문에(= 표현력이 떨어지기 때문에) 비선형 함수를 사용하는 것이다.
4. 활성화 함수의 종류(1) : 이진 계단 함수(Binary Step Function)
이진 계단 함수(Binary Step Function) 는 들어온 입력이 특정 입계점을 넘으면 1(혹은 True)를 출력하고 그렇지 않을 때는 0을 출ㄹ겨하기 때문이다. 이러한 특성 때문에 이 활성화 함수는 간단한 이진 분류 문제에서 유용하게 쓰인다.
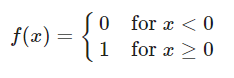
이진 계단 함수 예시 코드
def binary_step(x, threshold=0): # threshold가 있는 함수를 쓰면 꼭 defualt 값을 설정해주세요 return 0 if x<threshold else 1 import matplotlib.pyplot as plt from PIL import Image import numpy as np def plot_and_visulize(image_url, function, derivative=False): X = [-10 + x/100 for x in range(2000)] y = [function(y) for y in X] plt.figure(figsize=(12,12)) # 함수 그래프 plt.subplot(3,2,1) plt.title('function') plt.plot(X,y) # 함수의 미분 그래프 plt.subplot(3,2,2) plt.title('derivative') if derivative: dev_y = [derivative(y) for y in X] plt.plot(X,dev_y) # 무작위 샘플들 분포 samples = np.random.rand(1000) samples -= np.mean(samples) plt.subplot(3,2,3) plt.title('samples') plt.hist(samples,100) # 활성화 함수를 통과한 샘플들 분포 act_values = [function(y) for y in samples] plt.subplot(3,2,4) plt.title('activation values') plt.hist(act_values,100) # 원본 이미지 image = np.array(Image.open(image_url), dtype=np.float64)[:,:,0]/255. # 구분을 위해 gray-scale해서 확인 image -= np.median(image) plt.subplot(3,2,5) plt.title('origin image') plt.imshow(image, cmap='gray') # 활성화 함수를 통과한 이미지 activation_image = np.zeros(image.shape) h, w = image.shape for i in range(w): for j in range(h): activation_image[j][i] += function(image[j][i]) plt.subplot(3,2,6) plt.title('activation results') plt.imshow(activation_image, cmap='gray') return plt import os img_path = os.getenv('HOME')+'/aiffel/activation/jindo_dog.jpg' ax = plot_and_visulize(img_path, binary_step) ax.show()
📄Output
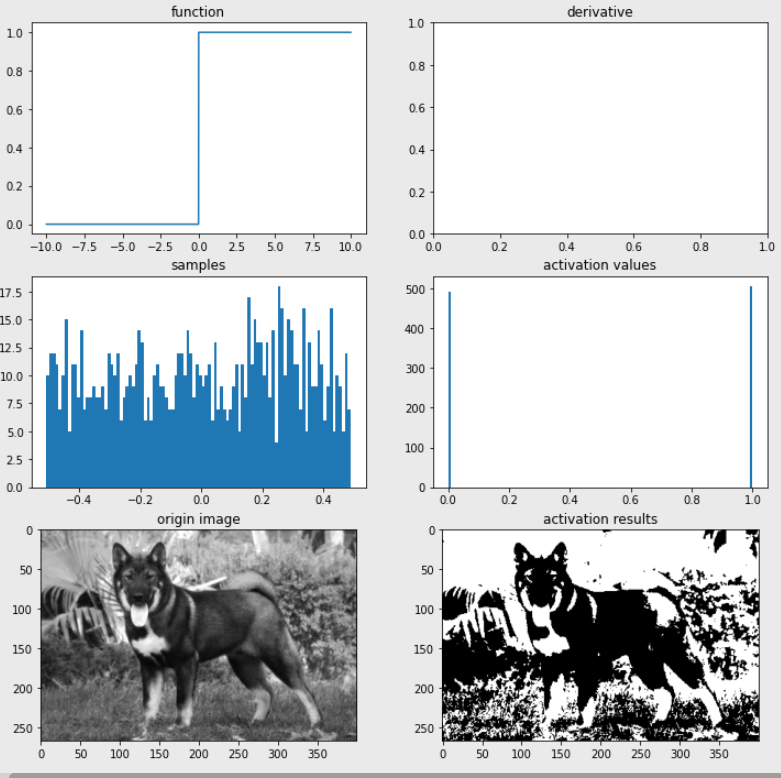
💡Tip 이진 계단 함수의 한계
1. XOR Gate를 구현할 수 없다.
XOR Gate의 진릿값 그래프를 하나의 선으로 구분을 할 수 없기 때문에 구현할 수 없지만 이를 해결하기 위해 다층 퍼셉트론(Multi-Layer Perceptron,MLP)를 사용한다.2. 역전파 알고리즘을 사용하지 못한다.
계단 함수는 0에서는 미분이 안 되고 0인 부분을 제외하고 미분을 한다고 해도 미분 값이 전부 0이 나온다. 따라서 가중치들이 업데이트됮 않아 역전파 알고리즘을 사용하지 못한다.
5. 활성화 함수의 종류(2) : 선형 활성화 함수(Linear Activation Function)
선형 활성화 함수를 사용한 모델은 이진 계단 함수를 사용한 모델과 다르게 다중 출력이 가능하기 때문에 이진 분류와 간단한 다중 분류 문제도 해결할 수 있다.
또한 미분이 가능해서 역전파 알고리즘도 사용가능하다.
의 선형 함수 예시 코드
import os img_path = os.getenv('HOME')+'/aiffel/activation/jindo_dog.jpg' # 선형 함수 def linear(x): return x def dev_linear(x): return 1 # 시각화 ax = plot_and_visulize(img_path, linear, dev_linear) ax.show()
📄Output
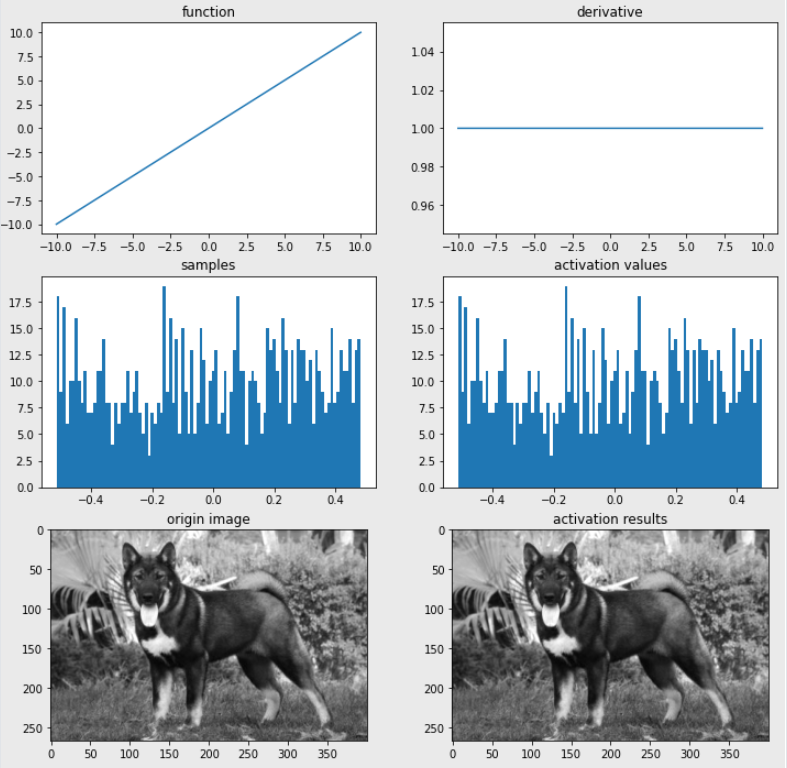
💡Tip 선형 활성화 함수의 한계
1. 모델에 선형 활성화 함수를 사용한다면 비선형적 특성을 지닌 데이터를 예측하지 못한다.
6. 활성화 함수의 종류(3) : 비선형 활성화 함수(Non-Linear Activation Function)
비선형 활성화 함수는 활성화 함수로써 나왔던 문제점을 해결한 함수로 역전파 알고리즘을 사용할 수 있으며 다중 출력도 가능하고 비선형적 특성을 지닌 데이터도 예측할 수 있다.
6-1. Sigmoid Function
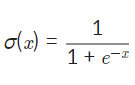
시그모이드는 위와 같은 식으로 표현되며 함수의 치역은 인데 이것이 시그모이드 함수를 쓰는 가장 주된 이유이다.
💡Tip Sigmoid 함수는 확률을 예측해야 하는 모델에서 자주 사용된다.
Sigmoid Function의 미분과 예시 코드
1. 미분 과정
- 예시 코드
import os img_path = os.getenv('HOME')+'/aiffel/activation/jindo_dog.jpg' # 시그모이드 함수 def sigmoid(x): return 1/(1+np.exp(-x).astype(np.float64)) def dev_sigmoid(x): return sigmoid(x)*(1-sigmoid(x)) # 시각화 ax = plot_and_visulize(img_path, sigmoid, dev_sigmoid) ax.show()
📄Output
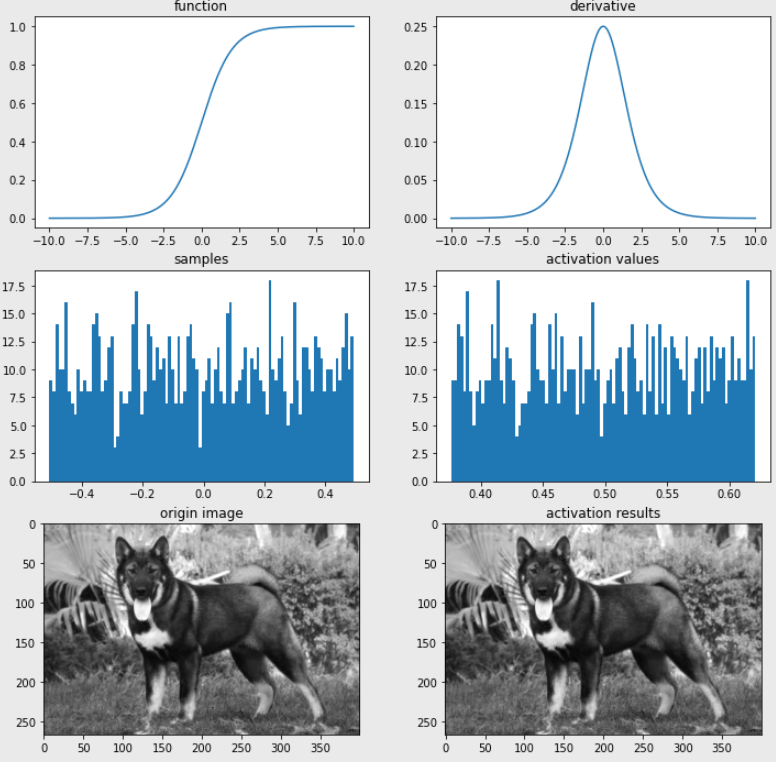
- Sigmoid Function의 단점
-
Sigmoid Function은 또는 에서 포화(Saturate) 된다. 이는 입력값이 아무리 커져도 함수의 출력은 에 더 가까워질 뿐 이상으로 높아지지 않고 반대로 입력값이 아무리 작아져도 함수의 출력은 에 가까워지기만 하고 이하로 떨어지지 않는다.
이렇게 포화가 발생하는 것을 Gradient가 에 근접한다는 뜻으로 이는 역전파에서 앞에서 온 역전파 값에 곱해지는 과정에서 이후의 역전파 값이 에 근접하게 되는 사실상 가중치의 업데이트가 일어나지 않는 Kill the Gradient상태가 된다.
따라서 아무리 훈련을 많이 해도 훈련의 효과가 거의 없다.
-
Sigmoid Function의 출력은 0이 중심(zero-centered)이 아니다.
이는 훈련의 시간이 지나치게 오래 걸리게 된다는 문제가 발생하며 만약 입력값으로 들어오는 데이터의 값이 모두 양수라고 가정하고 모델에 있는 어떠한 노드의 출력값이 라고 할 때 이 노드의 가중치 업데이를 위해 구해야하는 Gradient는 아래와 같다.
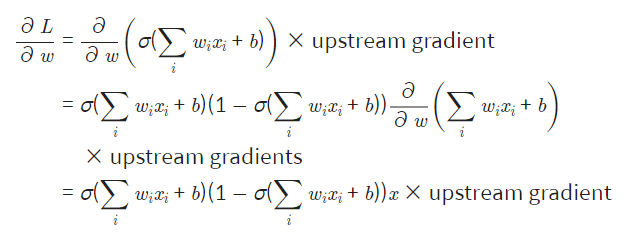
여기서 은 이고 는 노드 하나의 가중치 인데 의 와 가 모두 양수이기 때문에 결국 Upstream Gradient가 되고 노드의 가중치는 모두 양의 방향으로 업데이트 되거나 모두 음의 방향으로 업데이트가 되어 최적값을 향해 직선적으로 업데이트 되는 것보다 훨씬 긴 시간을 필요로 하게된다.
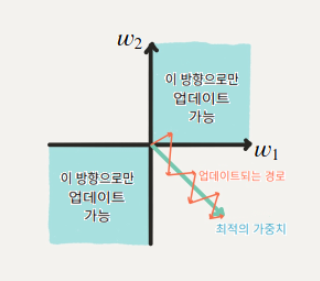
이러한 이유로 현재 Sigmoid Function은 잘 사용되지 않는다.
6-2. Softmax
Softmax는 사진을 구분하고 불류하는 문제에서 많이 쓰이는 함수로 Sigmoid와 다르게 Class수의 제한이 없기 때문에 각 Class의 확률을 구할 때 쓰이는 함수이다.
6-3. tanh(Hyperbolic Tangent)
tanh는 쌍곡선 함수 중 하나로 아래와 같이 표현된다.
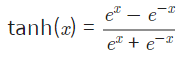
tanh의 치역은 이며 Sigmoid Function이 이 중심이 아니였던 것과 다르게 을 중심으로 하고 있기 때문에 Sigmoid Function보다 더 빨리 훈련이 이루어진다.
tanh의 미분과 예시 코드
1. 미분 과정
2. 예시 코드import os img_path = os.getenv('HOME')+'/aiffel/activation/jindo_dog.jpg' # 하이퍼볼릭 탄젠트 함수 def tanh(x): return (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x)) def dev_tanh(x): return 1-tanh(x)**2 # 시각화 ax = plot_and_visulize(img_path, tanh, dev_tanh) ax.show()
📄Output
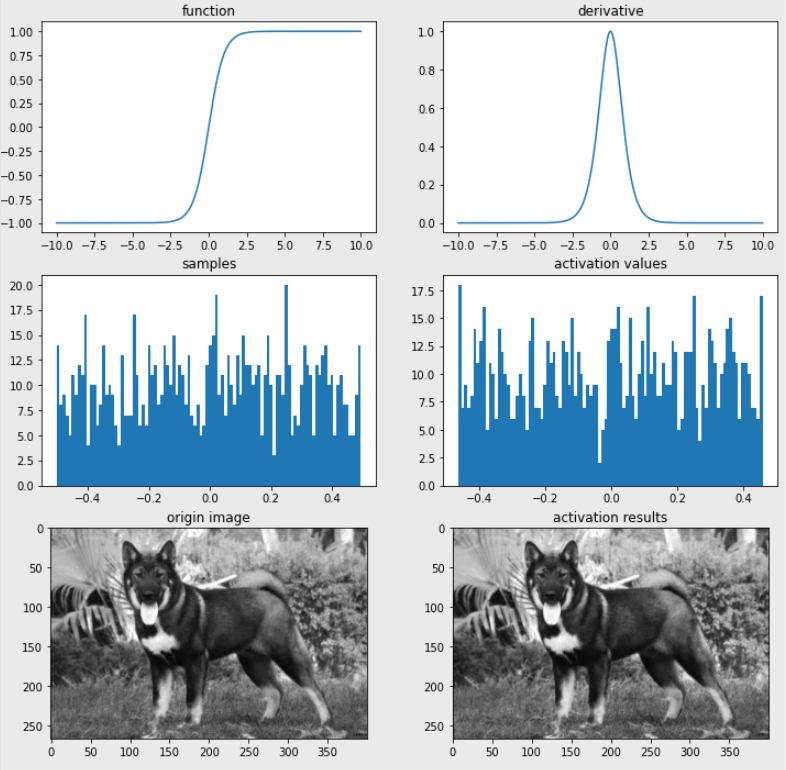
- tanh 함수의 단점
그래프에서 보이듯이 -1과 1에서 포화가 되는 단점을 극복하지 못했다.
6-4. ReLU(Rectified Linear Unit)
ReLU는 최근 가장 많이 사용되는 활성화 함수로 아래와 같이 표현된다.
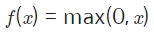
ReLU의 치역은 이며 tanh보다 훨씬 빠르게 훈련이 가능하다.
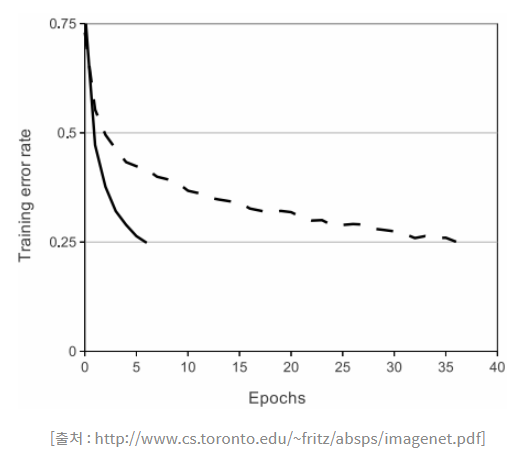
위의 그래프는 훈련 에러 비율을 나태내고 있으며 실선이 ReLU이고 점선이 tanh이다.
ReLU는 비용이 높은 exp와 같은 연산을 사용하지 않기 때문에 처리 속도가 빠르다.
- ReLU의 단점
ReLU의 출력값은 이 중심이 아니기에 일어나는 문제점들과 Dying ReLU의 문제이다. Dying ReLU는 사용한 노드가 비활성화되며 출력을 으로만 하게 되는 것이다.
이는 학습률을 조절하면서 발생 빈도를 낮출 수 있는데 학습률을 줄여준다면 이 문제는 적게 발생한다.
6-5. ReLU의 단점을 극복하기 위한 시도
-
Leaky ReLU
Dying LeLU를 발생시켰던 0을 출력하던 부분을 아죽 작은 음수값을 출력하게 만들어 해당 문제를 해결했으며 이 부분을 제외하고 ReLU와 같은 특성을 가진다. -
PReLU(Parametric ReLU)
Leaky ReLU와 유사하지만 새로운 파라미터를 추가하여 미만일 때의 기울기가 훈련되게 했다. -
ELU(Exponential Linear Unit)
ReLU의 모든 장점을 포함하며 이 중심점이 아니었던 단점과 Dying ReLU문제를 해결한 활성화 함수이다.
하지만 이 함수는 exponential 연산이 들어가서 계산 비용이 높다라는 단점이 있다.