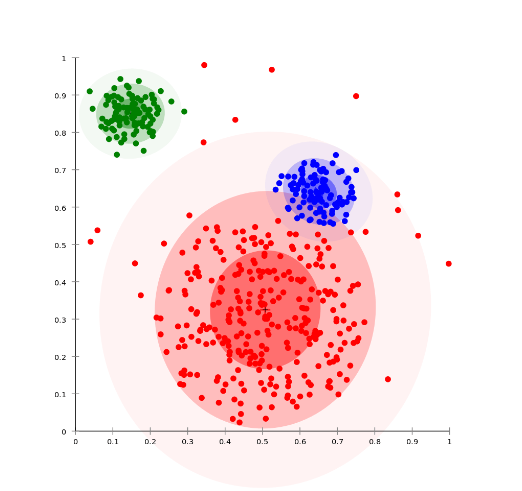
Clustering (K-Means, DBSCAN) (1)

Clustering

Dataset의 모든 Sample들을 비슷한 특징의 Group(cluster)으로 분배하는 과정이다.

갑자기 공부 시작 전에 Clustering와 Classification은 차이가 무엇인지 궁금했다. 바로 지도학습(분류)이냐 비지도학습(군집화)이냐 차이가 있었다. (이것은 매우 큰 차이이다!!!!)

아래에는 총 3가지 clustering 기법(K-Means, K-Nearest Neighbors, DBSCAN)을 소개한다. 먼저, K-Means에 대해 알아보자.

K-Means

각각의 Sample들을 K개의 Centroid 중 가까운 Cluster로 편성한다. 이후, Centroid는 Mean으로 최신화 후 다시 Clustering한다.
(기억이 잘남기 위해서는 K-Means이름과 개념을 동시에 생각하자 !!! )

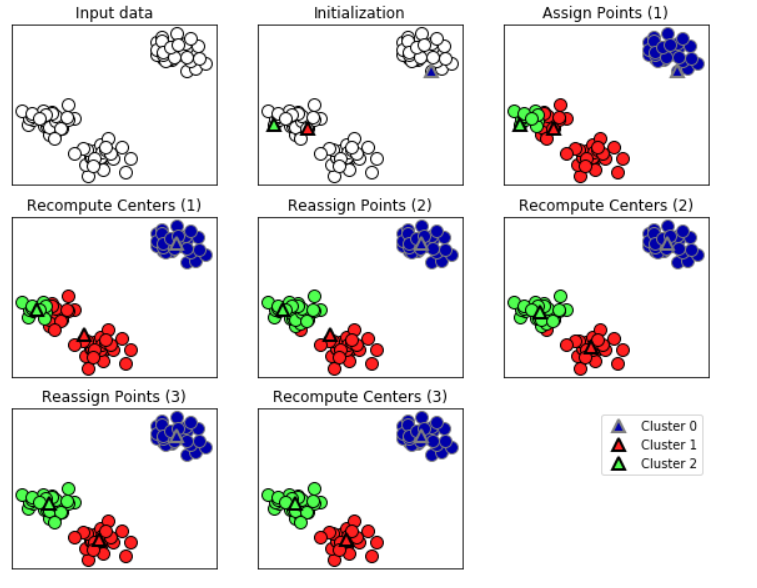
위의 사진순을 따라서 이해해보자.

1. Input data: 2차원에서 sample들이 나열되어 있다. (현재, 흰 색점인데 비지도 학습이라 Label이 없는 것을 확인하자.)

2. Initialization: k개의 Centroid 초기화 하는 것이다. (이때, centroid는 Cluster을 대표하는 값이라 생각하자.)

3. Assign Points(1): 이후, 위에 Input data(흰 색점)을 k개의 Centroid 중 가장 가까운 곳으로 clustering한다.

4. Recompute Centers(1): Centroid를 Clustering된 데이터들의 평균으로 최신화 시킨다.

5. Reassign Points(2): 최신화 된 Centroid로 data들을 다시 Clustering 시킨다.

6. Recompute Centers(2): 다시 Cluster의 data들의 평균으로 Centroid를 최신화 시킨다.

이제, 클러스터링 방법이 반복의 과정이라는 것을 눈치챘을 것이다. 아래의 7,8번 과정의 답을 위와같이 말해보자!!

7. Reassign Points(3)
8. Recompute Centers(3)

이제, 실습코드를 통해 kmeans를 실제로 어떻게 쓰는지 알아보자.

• 데이터셋 준비

from sklearn.datasets import make_blobs
import numpy as np

centroid = np.array(
    [[ 0.2,  2.3],
     [-1.5 ,  2.3],
     [-2.8,  1.8],
     [-2.8,  2.8],
     [-2.8,  1.3]])
std = np.array([0.4, 0.3, 0.1, 0.1, 0.1])

# 이 make_blobs 데이터셋을 쓴 이유는 아래에 k-means 클러스터링 단점에서 알아보자.
X, y = make_blobs(n_samples=2000,centers=centroid,
				 	cluster_std=std,random_state=7)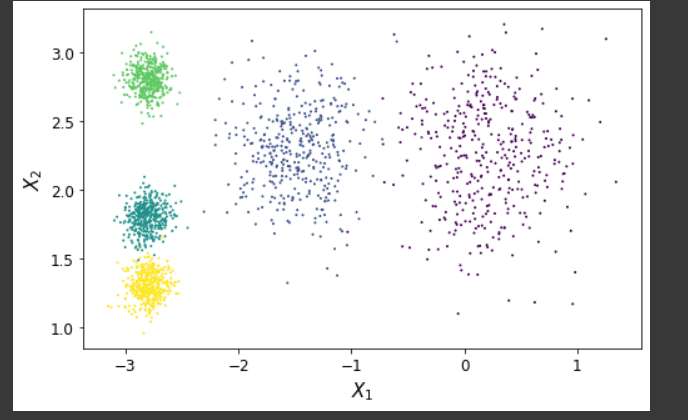

• kmeans 모델 만들기.

from sklearn.cluster import KMeans

k = 3
k_means = KMeans(n_cluster = k)
y_pred = k_means.fit_predict(X)

• Q k_means.fit vs k_means.fit_predict ? (조금 더 공부해보자.)

1. kmeans.fit: Fit후에 k_means.labels을 반환하지 않는다.
2. kmeans.fit_predict: Fit후에 k_means.labels을 반환한다.

K-Means의 2가지 고려사항

1. 초기 Centroid 설정하기

1-1 kmeans를 여러 번 시행해서 제일 좋은 centroid를 찾기
초기 centroid가 다른 모델을 100개 만들어서 그 중 제일 좋은 성능을 내는 모델을 가져오는 방법이다. 이때, 좋은 성능은 이너셔가 제일 낮은 것이 좋은 성능을 내는 모델이다.

이너셔는 Sample이 속한 클러스터의 Centroid거리의 제곱의 합을 다 더한 것이다. 수학 기호로 보면 쉽게 파악가능하다.
$\sum_{i=1}^K$ $\sum_{j=1}^N ||S_j-C_i||^2$ ( 이때, k는 클러스터 갯수이고 N은 해당 클러스터에 속한 데이터의 수이다. )

1-2. kmeans++로 Centroid 설정하기
처음 centroid는 kmeans와 동일하게 무작위로 한 개를 뽑고 2번째 centroid부터 처음 뽑힌 centroid와 가장 멀리있는 sample이 2번째로 centroid가 될 가능성이 제일 높게 설정해 확률적으로 뽑는다.

2. 적절한 Cluster k 수 찾기

클러스터 갯수가 무조건적으로 많게 하여 이너셔를 줄이는 방법은 좋지않다. 왜냐하면, 이미 잘 정의된 클러스터를 불필요하게 쪼개는 것이기 때문이다.

2-1 K의 이너셔를 구해 엘보우 찾기.

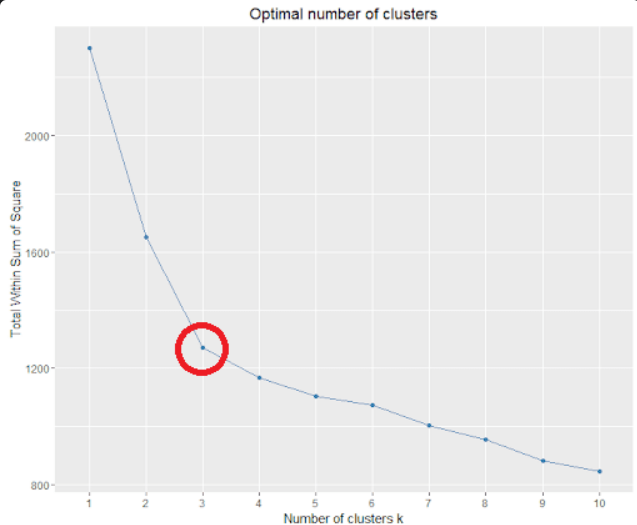
이너셔를 구하는 방법은 위에 소개가 되어있다. 이후, 클러스터 개수를 1개씩 늘려가며 클러스터 개수 당 이너셔점수를 계산하고 변동폭이 작아지는 곳을 k로 설정한다. 이때, 엘보우 찾기라고 한 것은 아래의 그림을 보면 확 꺽이는 부분이 팔꿈치와 닮아서 그렇게 부른다!
(이때, 적절한 k는 3이라고 할 수 있다. 2-3으로 변동할 때 기울기와 3-4 변동할 때 기울기 차이가 매우 크다.)

그림출처: https://itstory1592.tistory.com/17

2-2 실루엣 점수를 구해 K 찾기.

실루엣 점수를 구하는 과정은 계산비용이 올라가지만 위의 이너셔점수보다 더 신뢰성이 있는 K를 제시한다. 왜냐하면, 이너셔는 데이터 자신이 속한 클러스터의 Centroid만 고려해 점수를 매긴다.

반면에 실루엣점수는 Sample들이 자신의 클러스터의 Centroid 계산 and Sample 자신과 가장 가까운 다른 Cluster(Sample이 속한 Cluster는 제외)도 고려하여 값을 종합적으로 계산하기 때문이다. 아래의 수학식을 보면 더 쉽게 이해할 수 있다.

실루엣 점수 = 실루엣 계수들의 평균이다. 다음으로 실루엣 계수의 계산과정을 알아보기전에 용어들이 어려워보일 수 있는데 쉽게말해 실루엣 점수는실루엣 계수(즉, 해당 클러스터에 속한 각각의 Sample마다 실루엣을 구하는 것)를 구해 위에서 구한 같은 클러스터에 속한 Sample의 실루엣 계수를 평균하는 것이 실루엣 점수이다.

• 실루엣 계수 구하기

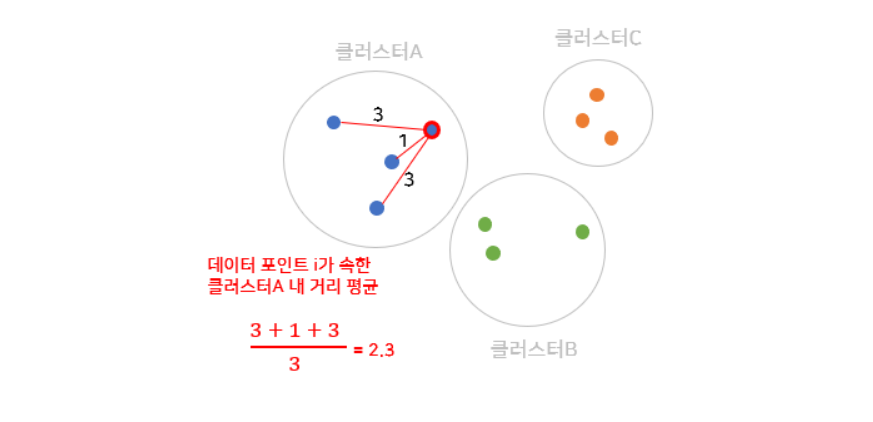
A: Cluster1 (Cluster A에는 N개의 Sample이 있다.)
$a_i$: N개중 i번째 Sample이 같은 클러스터 내에 다른 Sample과의 평균 거리이다.

그림출처: https://studying-haeung.tistory.com/10

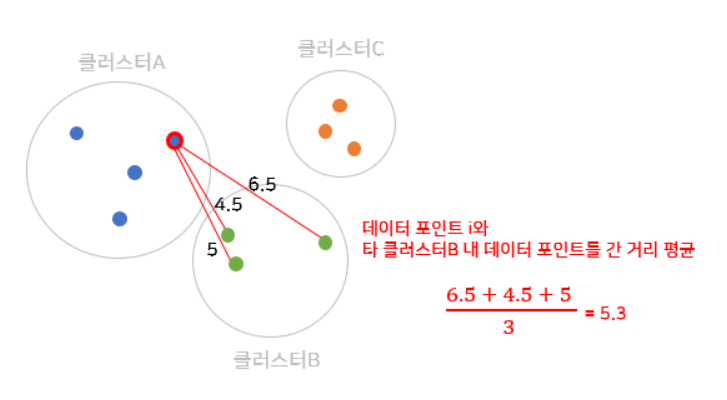
B: Cluster1과 가장 가까운 Cluster 2
$b_i$: A의 Cluster의 i번째 Sample과 Cluster 2의 모든 Sample의 평균거리이다.

그림출처: https://studying-haeung.tistory.com/10

실루엣 계수 = $\frac{b_i-a_i}{MAX{(a_i,b_i)}}$ (각각의 Sample마다 다 구해준다.)

그림출처: https://studying-haeung.tistory.com/10

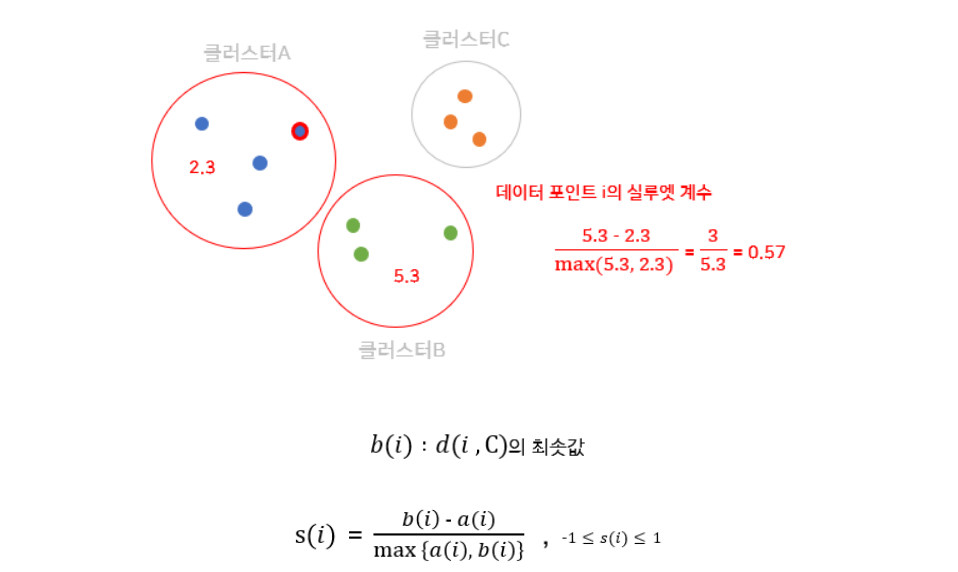
이제, 실루엣 점수를 구해봤으니 해석을 해보자.

실루엣 점수는 -1 ~ 1 의 값을 가진다. 1에 가까울 수록 좋은 클러스터링이 되었다고 생각할 수 있다. 왜냐하면, 위에 식을 분석했을때 1에 가깝다는 것은 분모에는 $b_i$가 MAX이고 분자는 $a_i$값이 작아서 b_i와 뺀 것이 미미하다는 것이다. 즉, 같은 클러스터 내에 있는 Sample들은 응집력있게 잘 뭉쳐져있고 다른 클러스터와의 거리는 매우 멀다고 기하학적으로 생각해보면 쉽게 이해가 간다.

좋은 클러스터 개수 k를 잡을 때 각 클러스터들이 평균 실루엣점수를 모두 넘고 클러스터의 속한 데이터의 개수가 균등한 것이 좋은 K라고 생각할 수 있다.

단점으로는 계산과정이 위에 이너셔보다 데이터의 개수에 따라 크게 늘어난다.

K-Means의 Pros & Cons

• Pros
  다른 Clustering 분석 방법보다 구현하기가 쉽고 속도가 빠르다.

• cons

1. 위에서 알아본 Centroid 초기값 문제와 K값을 설정. 따라서, Cluster의 개수와 outlier에 민감하다는 것을 알 수 있다.

2. Sample들의 분포가 원형이 아니라 타원이나 비선형적인 분포를 가지면 k-means로는 좋은 성능을 가지기 어렵다.

   왜냐하면, 우리가 Clustering 하고싶은 것이 타원이나 비선형적인 모양이라 가정하자. 그러면 k-means방식은 단순하게 Centroid에 거리가 가까운 Cluster로 Grouping하는데 이는 원형 이외에 다른 분포를 잘 잡지 못한다. 따라서, k-means를 실행하기전에 입력 특성의 scale을 맞춰서 최대한 타원형을 보정해주는 방식을 많이 사용한다.
   (그럼 타원과 비선형은 어떻게 클러스터링하지? 타원형: 가우시안 혼합 모델, 비선형: DBSCAN을 사용해 Clustering 한다.)
   

3. Sample들의 밀집도에 매우 민감하다.

아래의 밀집도의 차이로 첫 번째 예시처럼 2개의 Cluster를 원하지만 1개의 Cluster로 2번째 예시처럼 1개의 Cluster를 원하지만 2개의 Cluster로 학습될 수 있다.

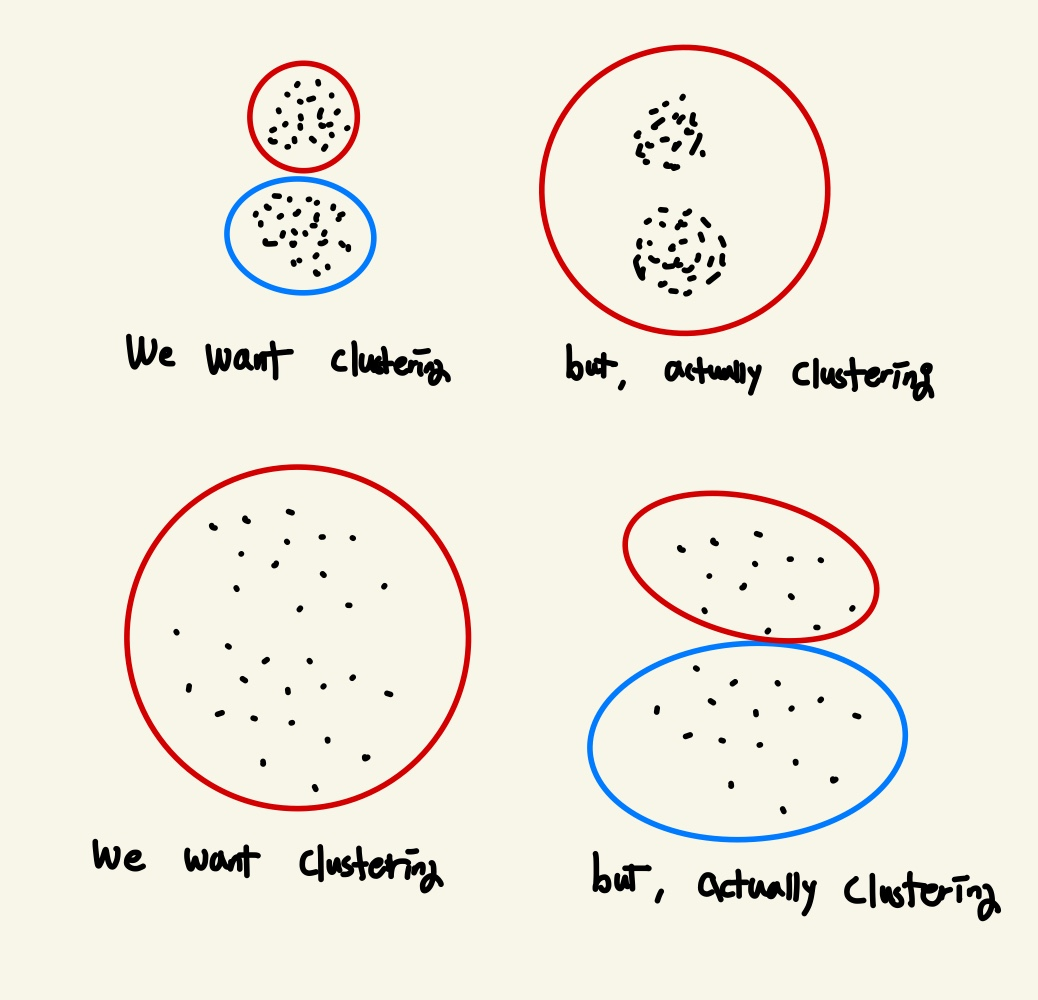
직접 그린 것이라 엉성해도 너그럽게 봐주시길 : )

DBSCAN (Density BaSed Clustering)

단순히 거리방식의 클러스터링이 아닌 밀집도(Density)를 기준으로 Clustering한다. 즉, 클러스터링전에 밀집도의 기준 2개를 정해준다. (기준 2개는 eps: 반경의 크기와 Minpts: 반경내에 포함되야하는 최소 Point 수이다.)

• 용어설명

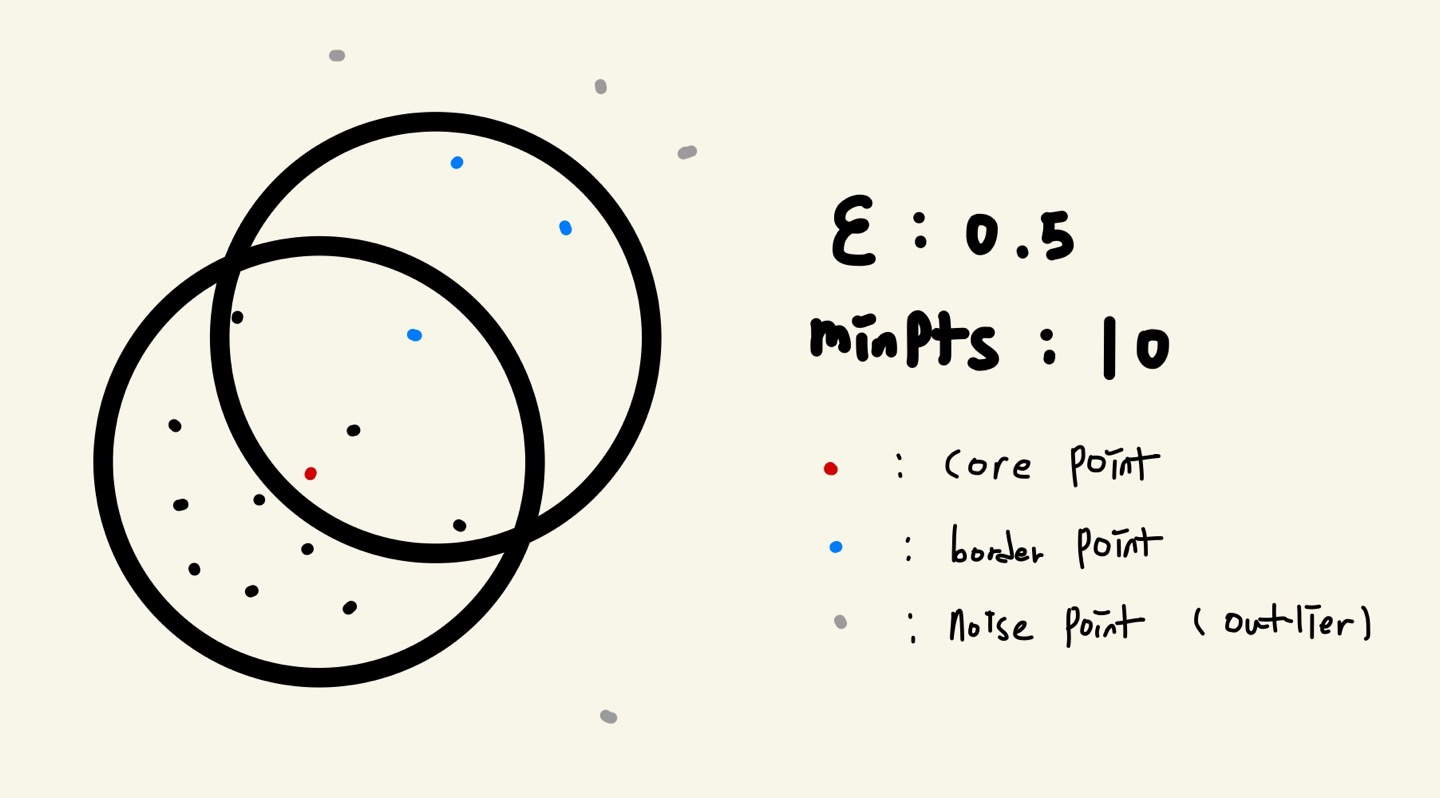
1. Core Point
   해당 점이 $\epsilon$ 반경내에서 MinPts수 이상(자신을 포함한)의 Point를 가지고 있으면 그 점을 Core Point라 한다.

2. Border Point
   CorePoint의 반경내에 존재하지만 해당 점이 $\epsilon$ 반경내에서 MinPts수 이하의 Point를 가지고 있을때 그 점을 BorderPoint라 한다.

3. Noise Point (Outlier)
   CorePoint 반경내에 속하지도 않고 $\epsilon$ 반경내에서 MinPts수 이하의 Point를 가지면 그 점을 Noise Point라 한다.

• 동작 방식

1. Random하게 Point를 잡는다. 그것의 $\epsilon$-neighbor의 개수를 찾는다.
2. 만약, $\epsilon$-neighbor의 개수가 훈련 전 Setting 한 MinPts를 넘는다면 해당 점을 CorePoint로 분류하고 해당 점과 neighbor을 같은 Label을 할당한다.
3. 이후, 모든 neighbor들이 BorderPoint인지 또다른 CorePoint인지 확인한다.
4. 3번과정에서 이웃이 CorePoint로 분류되면 위의 2,3과정을 반복한다.
5. 반복은 더 이상 CorePoint가 없을때까지 반복한다.

DBSACN의 Pros & Cons

• Pros
  위에서 소개했던 Kmeans의 어떤 문제점을 보완했는지 비교하면서 기억하자.

  k-means의 k는 비지도 학습에서 Label을 모르는 상태로 Cluster개수를 정하기 어렵다. 하지만, DBSCAN은 반경과 MinPts만 입력해주면 Cluster개수를 데이터를 돌면서 밀집도에 따라 나눠준다.

  K-means는 Algorithm 특성 상 원형으로 된 cluster밖에 만들지 못한다. 하지만, DBSCAN은 타원, 비선형 경계(지렁이 모양 등등)을 밀도기반으로 잘잡아낸다.

  그리고 가장 중요한 사항은 k-means는 이상치를 제외하지않고 모두 클러스터링 해주었는데 DBSCAN은 밀집도가 일정이하이면 그것을 이상치로 추정해 Cluster하지않고 그대로 나둔다. 따라서, 더 좋은 학습을 일으킨다.

• Cons

1. 적절한 $\epsilon$ 과 Minpts를 찾는 것이 어렵다
2. k-means보다 계산량이 많다. (밀도를 계산할 때 모든 point간의 거리를 계산해야하여서차원이 커질 수록 더 어려워진다. )