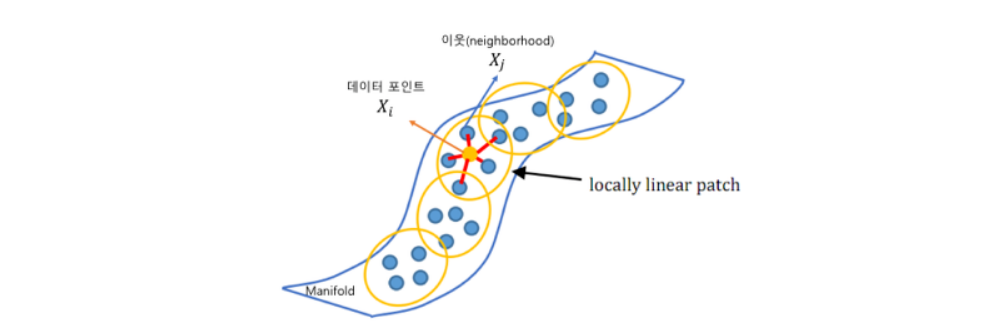
LLE (Locally Linear Embedding)
앞에서 공부했던 PCA는 선형으로 투영했을때 분산이 가장 큰 축을 기준으로 차원을 축소해나갔다. 이번에 공부할 LLE는 비선형 차원축소에 해당한다.
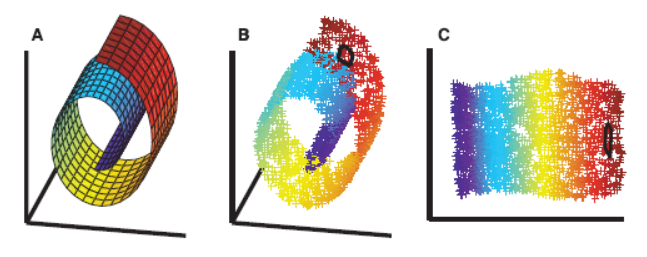
먼저, 위와같이 3차원에서 스위스롤과 같은 형태로 데이터가 분포해 있을때, PCA와 MDS 차원축소 방법을 사용하면 데이터의 분포를 살리기 힘들다. 이때, 위의 사진과 같이 매니폴드를 잡아서 데이터의 차원을 축소해나가야한다.
이를 매니폴드 학습법이라고 한다.
그 중 LLE는 머신러닝 알고리즘 중 Unsupervised Learning에 해당하며, 서로 인접한 데이터 (Locally) 들을 보존(neighborhood-preserving)하면서 고차원인 데이터셋을 저차원으로 축소하는 방법이다.
LLE Algorithm
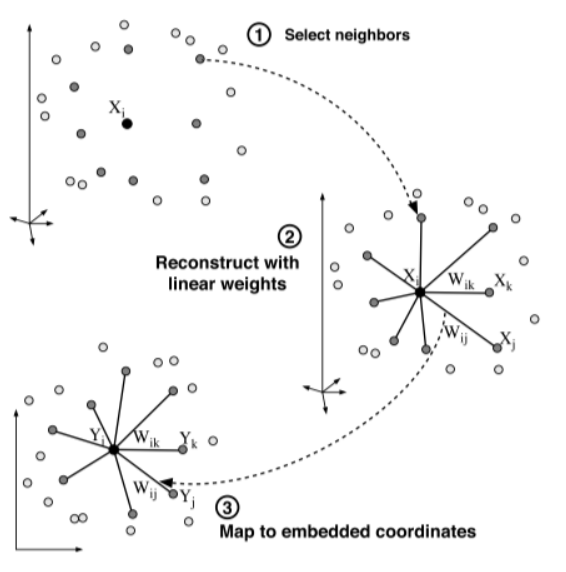
Suppose) M개의 데이터, N개의 Feature, K개의 neighbors
전체적인 Algorithm과정의 핵심은 한 데이터의 차원을 축소했을 때 주위 데이터와의 분포를 축소 전의 상태와 최대한 유사하게 차원을 축소시키는 것이다.
Step 1: Select Neighbors (user set parameter k)
모든 M개 각각의 데이터 기준으로 k개의 가까운점을 찾는다.
: M개의 데이터 중 i번째 (i = 1, ... ,M)
: i번째 데이터 기준으로 j번째 이웃 (j = 1, ... ,K)
: i번째 데이터 기준으로 j번째 이웃의 가중치
Step 2: Set the optimum Linear weight.
아래의 식은 k개의 이웃들마다 최적화된(즉, 를 잘 표현하는)가중치를 부여해서 가 실제값 와의 오차가 가장 작게 만드는 것이 목적이다.
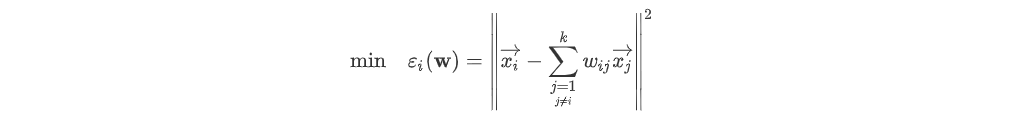
이때, 제약조건으로 가중치들의 합은 1로 유지해야한다.
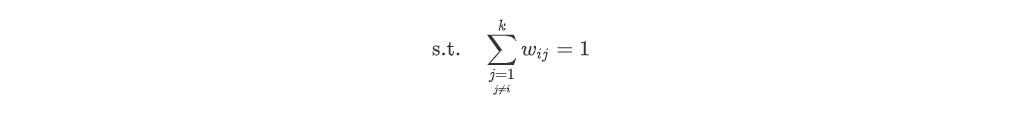
Now, 를 어떻게 구하는지 알아보자. 아래의 식은 를 최소화 할때는 vector 를 더하고 빼도 error의 최소가 되는 W는 바뀌지 않는다.
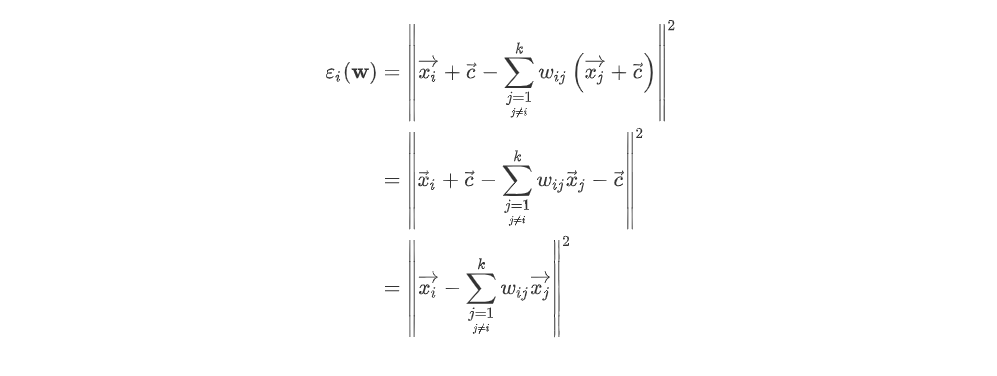
이때, vector c를 라고 가정하자. 그러면 아래의 식이 나온다.
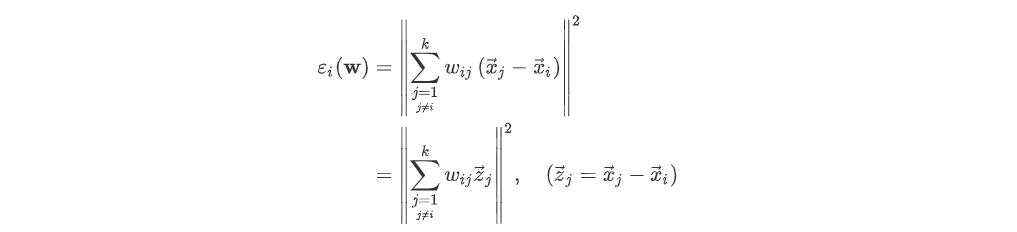
= 이라하면, 은 K X 1 크기의 행렬이다.
= 이라하면, 은 K X N 크기의 행렬이다.
이후, 식을 아래와 같이 나타날 수 있고 는 Symmetic matrix이다. (왜냐, pca와 같은 의미로 Covariance matrix가 되어버려서)
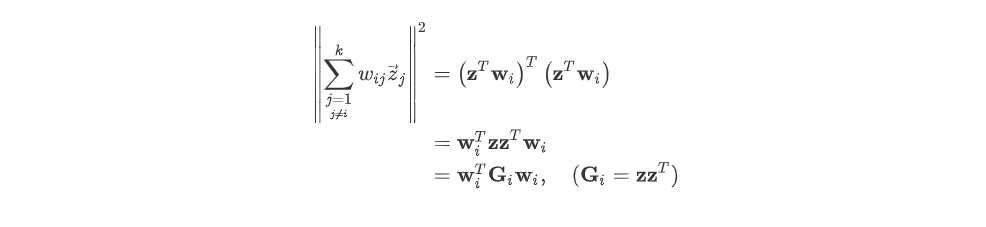
이후, Min 한 최적화 W를 찾아야하니 라그랑주 승수법을 이용한다. 그러면 아래의 식을 편미분하여 넘기면 Optomal 한 i번째 데이터의 k개의 이웃 가중치를 구할 수 있다.
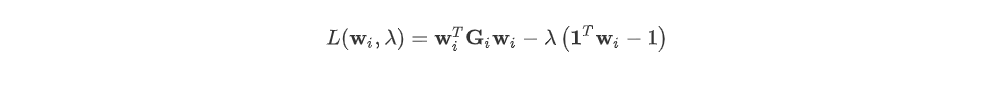
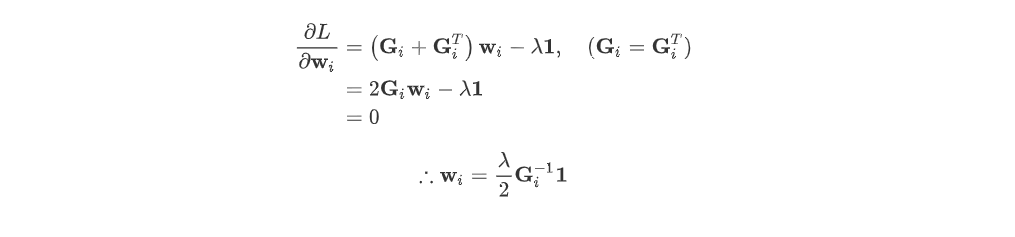
Step 3: Map to embedded coordinates
Step 3의 목적은 차원을 축소해서 얻은 데이터와 이웃 역시 차원축소해 나온 값 multiple 가중치의 오차가 최소가 되는 것이다. 이를 식으로 표현하면 아래와 같다.
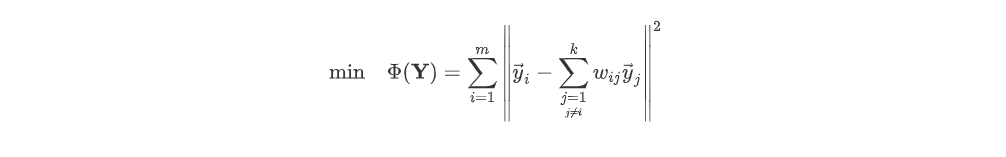
이때, 제약조건으로 d차원 공간상에 매핑된 M개의 데이터셋()에서 데이터 포인트 의 평균은 0이고, Y의 공분산(covariance)는 (identity) 행렬인 것을 알 수 있고, 은 symmetric 한것을 알 수 있다.
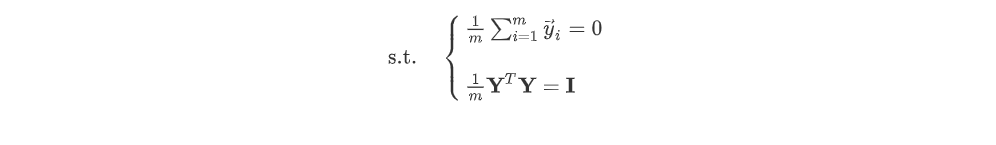
이제, 아래의 식을 행렬로 나타내 다시 표현하면 아래와 같고 전개를 해주면 가 나온다.
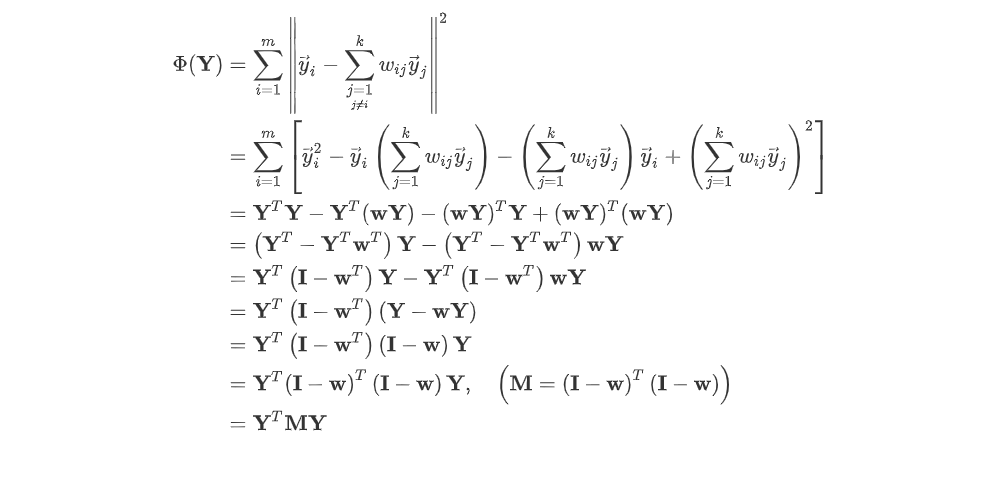
이후, 최적해를 구하기위해 라그랑주 승수법으로 표현하면 아래와 같다.
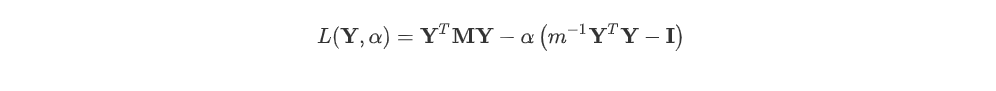
Y의 최적화를 알고싶은 것이니 L을 Y로 편미분을 취한값이 0이 되는 Y를 찾는다. 이때, 최종식이 = 가 된다.
이는 는 의 eigenvectors 인 것을 알 수 있고, 은 eigenvalue인 것을 알 수 있다.
위의 문제는 를 찾는 것이며, PCA와는 다르게 중에서도 가장 값을 최소화하는 eigenvector인 맨 오른쪽에 위치하는 열벡터이다.
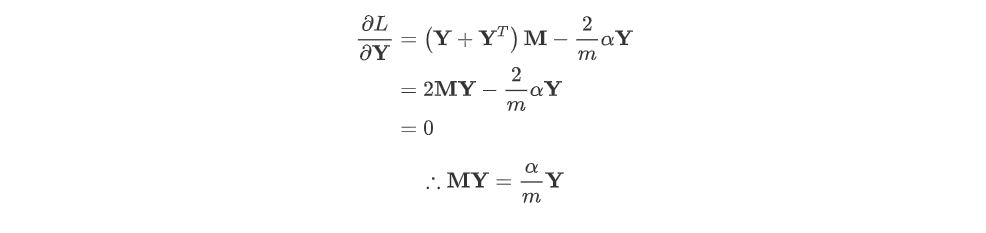
결국, 우리가 찾은 는 아래와 같이 축소할 평면(즉, 매니폴드)를 찾은 것이다.