Dimension Reduction - PCA

HyeonGi_Jeong·2023년 2월 13일

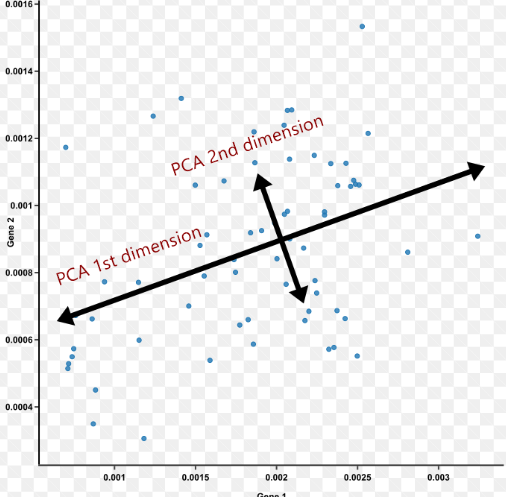
PCA

다차원 데이터의 분포를 최대한 유지하며 저차원의 데이터로 표현하는 것이다. 이때, 첫번째 축을 잡을 때 데이터를 정사영했을때 분산이 가장 큰 축으로 잡아야한다.

Covariance Matrix의 Eigenvalue가 최대 variance인 이유

최대 Variance가 데이터의 분포를 가장 잘 표현하는 이유

아래의 그림에서 파란색 표시는 i번째 Sample을 벡터 u에 정사영 시켰을 때 오차를 말한다. 모든 sample이 벡터 u에 정사영했을때 error를 최소가 되는 벡터 u를 찾는 것이 목적이다.

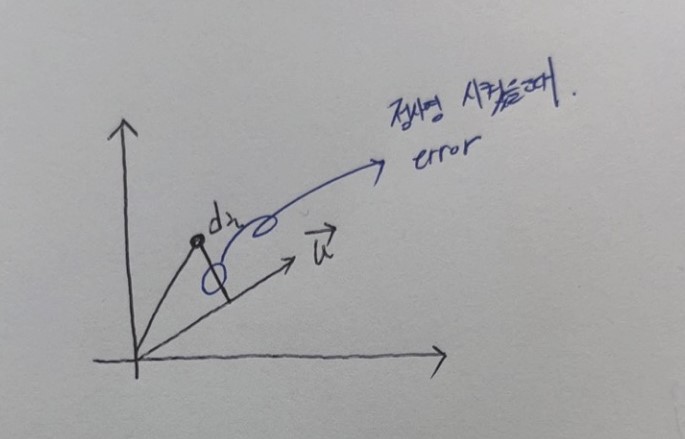
Let, u는 unit vector이다. 따라서, $u의 크기 = sqrt(u^Tu) = u^Tu = 1$
원점으로 데이터 sample을 이동시켜주는 작업을 한다.
Suppose that $d_\mu$ = sample들의 평균, $d_i^-$ = 실제 값, $d_i$ = $d_i^-$ - $d_\mu$ = 평균을 0으로 이동한 값

Min $\frac{1}{n}$ $\sum_{i=1}^{n} (d_i - (d_i^Tu)u)^T(d_i - (d_i^Tu)u)$ 되는 u를 찾는 것이 목적이다.

전개하면 $\frac{1}{n}$ $\sum_{i=1}^{n}d_i^Td_i - d_i^T(d_i^Tu)u - (d_i^Tu)u^Td_i + (d_i^Tu)u^T(d_i^Tu)u$

이때, $(d_i^Tu)u^T(d_i^Tu)u$ = $(d_i^Tu)(d_i^Tu)u^Tu$ = $(d_i^Tu)(d_i^Tu)$ = $(d_i^Tu)^2$ 이다.
( 왜냐하면, 가정에 의해 $u^Tu = 1$ 이다. )

그리고, $d_i^T(d_i^Tu)u$ = $(d_i^Tu)d_i^Tu$ ( d_i^Tu는 scalar이다.) = $(d_i^Tu)^2$ 따라서, 위에 두개는 제거된다.

그리고, 우리가 찾고싶은 것은 u의 최적화이기 때문에 식에 필요없는 $d_i^Td_i$ 제거하고 생각해도 최적화된 u는 동일하다.

제거를 하고 난 뒤 남는 것은 min $\frac{1}{n}$ $\sum_{i=1}^{n}-(d_i^Tu)u^Td_i$ 이다. 그리고, $(d_i^Tu)$ , $u^Td_i$ 는 scalar라서 자리를 바꿔도 동일하다.

min $\frac{1}{n}$ $\sum_{i=1}^{n}-u^Td_id_i^Tu$ = min $\frac{1}{n}$ $\sum_{i=1}^{n}-u^T(d_i^-$ - $d_\mu)(d_i^-$ - $d_\mu)^Tu$

이때, $\frac{1}{n}\sum_{i=1}^{n}(d_i^-$ - $d_\mu)(d_i^-$ - $d_\mu)^T$ 를 자세히 보면 이는 Covariance matrix가 된다.(원래는 $\frac{1}{n-1}\sum_{i=1}^{n}(d_i^-$ - $d_\mu)(d_i^-$ - $d_\mu)^T$ 인데 최적화 문제에서는 1/n이나 1/(n-1)나 최적의 벡터 u는 동일하다.)

즉, 분산이 등장했다. 지금까지 처음 error(거리)에서 분산까지 차근차근 도출해왔다.

이제, $\frac{1}{n}\sum_{i=1}^{n}(d_i^-$ - $d_\mu)(d_i^-$ - $d_\mu)^T$ = $R_d$ = 공분산 행렬

Min $-u^TR_du$ = -Min $u^TR_du$ = Max $u^TR_du$ s.t. $u^Tu=1$

여기서, 등장하는 것이 최적해를 찾는 라그랑주 승수법이다. (라그랑주 승수법은 따로 포스팅 할 예정이다.)

L(u, $\lambda$ ) = $u^TR_du$ + $\lambda$ (1-u^Tu) ( $\frac{\delta L}{\delta u } = 0$ 이 되어야 Max하는 벡터 u이다. )

$dL_u$ = $du^TR_du$ + $u^TR_ddu$ - $\lambda du^Tu$ - $\lambda u^Tdu$

이때, $(\lambda du^Tu)^T$ = $\lambda u^Tdu$ , $(du^TR_du)^T$ = $u^TR_ddu$ 이다. 왜냐하면, scalar라서 transpose를 해도 동일하다.

따라서, $dL_u$ = 2 $u^TR_ddu$ - 2 $\lambda u^Tdu$ = (2 $u^TR_d$ - 2 $\lambda u^T$ ) du

(2 $u^TR_d$ - 2 $\lambda u^T$ ) = $\frac{\delta L}{\delta u }$ 이므로 (이 역시 따로 라그랑주 승수법과 같이 포스팅 하겠다. )

(2 $u^TR_d$ - 2 $\lambda u^T$ ) = 0이고 정리하면 $u^TR_d$ = $\lambda u^T$ transpose를 취해주면 $R_du$ = $\lambda u$ 가 되고 이는 우리가 많이 보았던 Eigendecomposition이 된다. 즉, 공분산 행렬의 고유값분해인 것이다. ( $R_d$ 는 Symmetic Matrix라서 Eigendecomposition이 가능하다. )

그러면, $R_du$ = ( $\lambda_1$ $q_1$ $q_1^T$ + $\lambda_2$ $q_2$ $q_2^T$ + ... + $\lambda_n$ $q_n$ $q_n^T$ )이된다. ( $\lambda_i$ 는 i번째 eigenvalue이고 $q_i$ 는 i번째 eigenvector이다. )

이제 식을 다시 쓰면 Max $u^T$ $R_d$ $u$ = Max $u^T$ ( $\lambda_1$ $q_1$ $q_1^T$ + $\lambda_2$ $q_2$ $q_2^T$ + ... + $\lambda_n$ ) $u$ 이 되고 이 값이 최대가 되는 값은 $\lambda_1$ 이 다른 $\lambda_i$ 보다 다 크니깐 u vector는 $q_1$ 이 되어야한다. (즉, 이것이 variance가 가장 큰 축을 잡는 것이다.) 그리고 다음은 자동적으로 $q_2$ 이다.