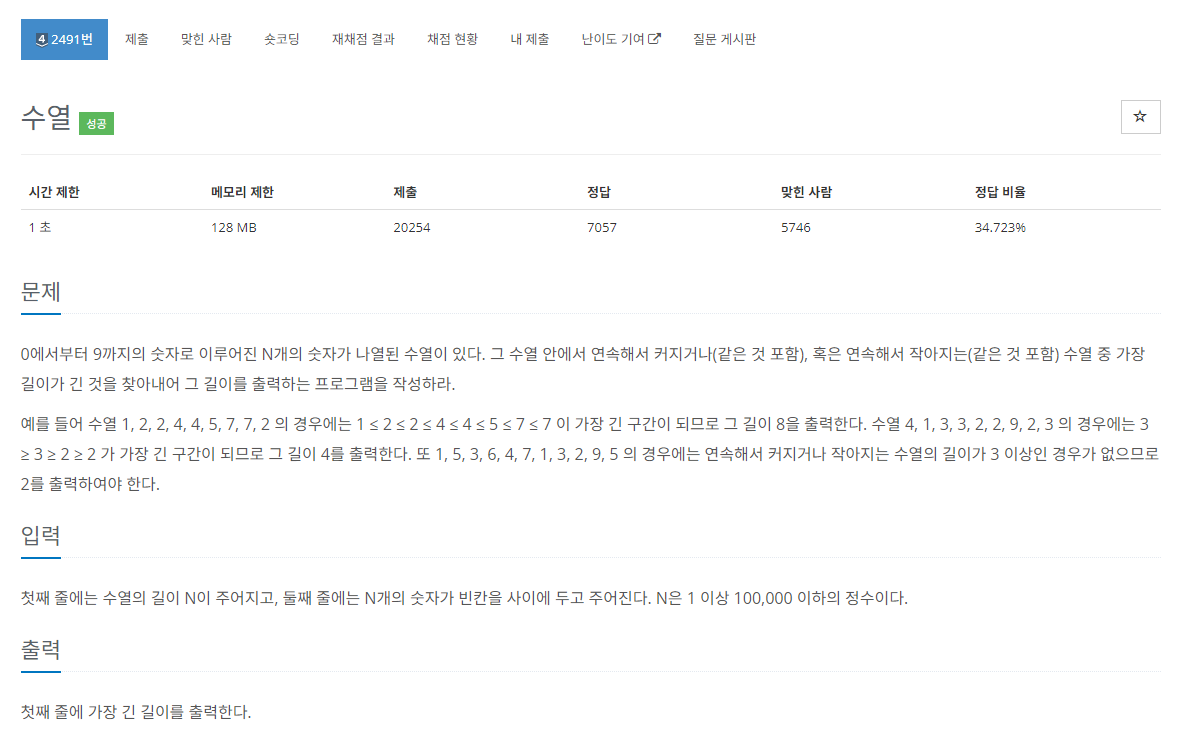
문제

---

https://www.acmicpc.net/problem/2491

코드

---

package baekjoon;

import java.io.*;
import java.util.*;

class Main {
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

		int N = Integer.parseInt(br.readLine());
		int[] arr = new int[N];

		StringTokenizer st = new StringTokenizer(br.readLine());
		for (int i = 0; i < N; i++) {
			arr[i] = Integer.parseInt(st.nextToken());
		}

		int max = 1;
		int increaseCount = 1;
		int decreaseCount = 1;
		for (int i = 1; i < N; i++) {
			// 증가하는 경우
			if (arr[i] >= arr[i - 1]) {
				increaseCount++;
			} else {
				increaseCount = 1;
			}

			// 감소하는 경우
			if (arr[i] <= arr[i - 1]) {
				decreaseCount++;
			} else {
				decreaseCount = 1;
			}

			max = Math.max(max, Math.max(increaseCount, decreaseCount));
		}

		System.out.println(max);
	}
}

문제 이해

---

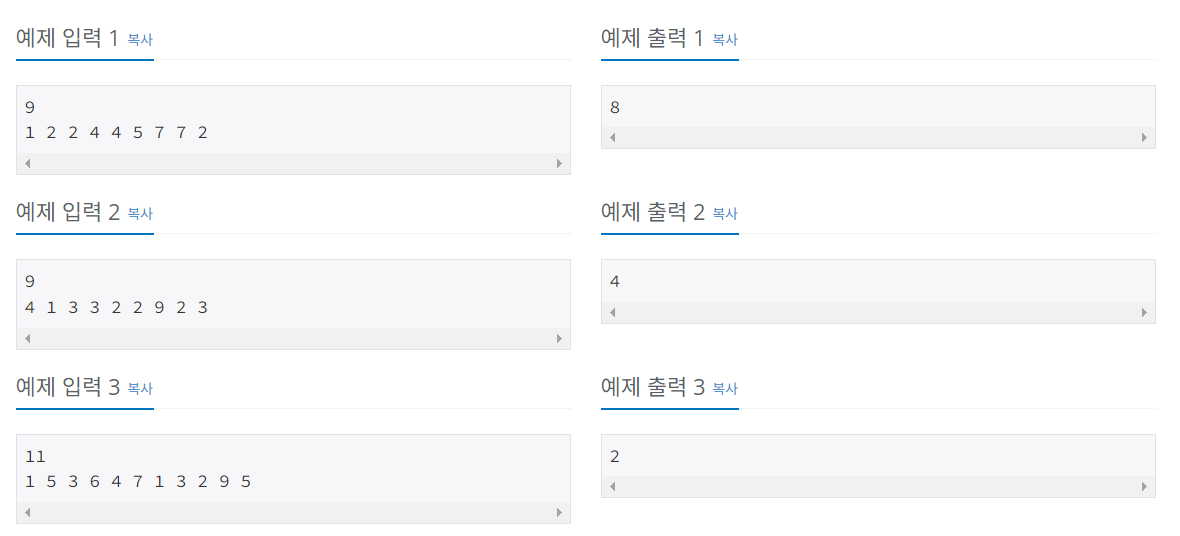
• 수열에서 수열이 연속해서 증가하거나 같은 경우, 혹은 감소하거나 같은 경우 중에 그 길이가 가장 긴 길이를 구하는 문제이다.

풀이 방법

---

• 문제 그대로 구현하면 된다.
• increaseCount와 decreaseCount를 구하고, 매 루프마다 max를 갱신하면 된다.

핵심 포인트

---

• max의 갱신을 매번 진행해주어야 한다.
• 처음 구현할 때 연속되는 부분이 끊기는 경우에서만 max를 갱신하도록 로직을 짰었다.
• 하지만 그렇게 구현하는 경우, 계속해서 같은 경우가 나오는 경우 갱신이 제대로 되지 않는다.
• 따라서 매번 갱신을 해주어야 한다.

보완할 점 / 느낀 점

---

• 위 문제의 경우, 찾아보니 dp로도 풀 수 있었다.
• 위 구현과 dp의 로직은 거의 유사하나, dp의 경우는 아래와 같은 점화식을 통해서 갱신한다.

  dp[i] = dp[i-1]+1 혹은 dp[i]=1

• 문제를 풀고나서 dp로도 풀어보니 dp에 대해서 더 이해할 수 있어 좋은 문제였다고 생각한다.

참고자료

---

DP풀이

import java.io.*;
import java.util.*;

class Main {
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

		int N = Integer.parseInt(br.readLine());
		int[] arr = new int[N];
		int[] dpSmall = new int[N];
		int[] dpBig = new int[N];

		StringTokenizer st = new StringTokenizer(br.readLine());
		for (int i = 0; i < N; i++) {
			arr[i] = Integer.parseInt(st.nextToken());
		}

		long max = 1;
		dpSmall[0] = 1;
		dpBig[0] = 1;
		for (int i = 1; i < N; i++) {
			// 증가하는 경우
			if (arr[i] >= arr[i - 1]) {
				dpBig[i] = dpBig[i - 1] + 1;
			} else {
				dpBig[i] = 1;
			}

			// 감소하는 경우
			if (arr[i] <= arr[i - 1]) {
				dpSmall[i] = dpSmall[i - 1] + 1;
			} else {
				dpSmall[i] = 1;
			}

			max = Math.max(max, Math.max(dpSmall[i], dpBig[i]));
		}

		System.out.println(max);
	}
}