3D Gaussian Splatting for Real-Time Radiance Field Rendering 논문 리뷰

논문 링크

https://arxiv.org/abs/2308.04079

해당 그림은 3D Gaussian Splatting의 결과 비교 사진입니다. 빠른 렌더링 속도와 고해상도가 해당 모델의 Contribution입니다. 논문의 흐름을 그대로 따라갔지만 중요한 부분만 보시고 싶으시다면 Overview로 바로 넘어가셔도 무방합니다.

Abstract

• 3D Gaussians: 카메라 캘리브레이션 과정에서 생성된 희소 포인트들로부터 출발하여, 장면을 3D Gaussians로 표현합니다. 이는 장면 최적화를 위해 연속적인 볼류메트릭 Radiance Fields의 유용한 속성을 유지하면서 불필요한 빈 공간에서의 계산을 피할 수 있습니다.
• Anisotropic Covariance: 3D Gaussians의 최적화 및 밀도 제어를 교차적으로 수행하면서 Anisotropic Covariance를 최적화하여 장면을 더 정확하게 표현할 수 있습니다.
• Visibility-aware Rendering Algorithm: Anisotropic Splatting을 지원하는 빠른 Visibility-aware Rendering Algorithm을 개발하여 학습을 가속화하고 실시간 렌더링을 가능하게 합니다.

Introduction

Mesh나 point를 사용해서 3D scene representation을 표현하는 방식은 GPU-resterization에 적절한 방식입니다. 이와 대조적으로 NeRF에서는 MLP를 최적화하는 방식으로 3D scene representation을 진행했습니다. NeRF의 결과는 놀라웠지만 많은 시간이 걸렸고 결과에 noise가 발생했습니다.

기존의 NeRF방식은 성능이 좋지만 시간이 오래걸렸고, 반대로 Radiance Field를 이용한 방식은 성능은 좋지 않지만 시간이 적게 걸립니다.

이에 해당 논문에서는 3D Gaussian representation 모델을 제시했습니다. 공개된 데이터를 기반으로 실시간성의 높은 화질의 이미지를 생성할 수 있습니다. Abstract에서 나와있는 것처럼 크게 3가지 mian components가 존재합니다.

1. 3D Gaussians

기존 NeRF 모델들처럼 SfM을 통해 얻은 Sparse Point Cloud를 활용하여 3D Gaussians를 초기화합니다. 3D Gaussians는 연속적이고 미분 가능한 볼륨 표현을 제공하면서도, 2D 이미지로 변환하기에 효율적이라는 점에서 장점이 있습니다.

1. optimization of the properties of the 3D Gaussians

3D position, opacity α, anisotropic covariance, and spherical harmonic (SH) coefficients

위의 방식들에서 다양한 최적화 방식을 사용했습니다. 이 부분에 대해서는 아래에 다시한번 자세히 설명하도록 하겠습니다.

1. real-time rendering

빠른 GPU 기반의 정렬 알고리즘을 사용하여 Visibility-aware Rendering을 구현합니다.

Reltated Work

Traditional Scene Reconstruction and Rendering

SfM은 카메라 보정 동안 sparse point cloud을 추정하며, 이는 처음에는 3D 공간을 간단히 시각화하는 데 사용되었습니다.
이후의 Multi-View Stereo (MVS) 기법은 수년 동안 인상적인 완전한 3D 복원 알고리즘을 개발하게 했으며, 이는 여러 뷰 합성 알고리즘의 발전을 가능하게 했습니다.

이러한 방법들은 훌륭한 결과를 제공하지만, 복원되지 않은 영역이나 MVS가 존재하지 않는 기하학을 생성하는 over-reconstruction에서 완전히 회복하지 못할 수 있습니다.

최근의 neural rendering 알고리즘은 이러한 arifacts를 크게 줄이고, 모든 입력 이미지를 GPU에 저장하는 비용을 피하면서 위의 한계를 극복했습니다.

Neural Rendering and Radiance Fields

초기에는 CNN을 활용하여 blending weights를 추정하거나 texture-space solution을 제공하는 방식이 사용되었습니다. 그러나 MVS(Multi-View Stereo) 기반 기하학을 사용한 것이 대부분의 방법에서 큰 단점으로 작용했고, CNN을 사용한 최종 렌더링은 종종 Temporal Flickering(시간에 따른 깜빡임) 문제를 야기했습니다.

Soft3D로 시작된 Volumetric Representations는 이후 Volumetric Ray-Marching과 결합된 딥러닝 기법들로 발전했습니다. 이 방법들은 기하학을 표현하기 위해 연속적인 미분 가능한 density field를 사용했지만, 볼륨을 쿼리하기 위해 많은 샘플이 필요해 비용이 많이 들었습니다.

NeRF는 Importance Sampling과 Positional Encoding을 도입해 품질을 개선했지만, MLP의 많은 사용은 속도에 부정적인 영향을 미쳤습니다. NeRF의 성공 이후, 품질과 속도를 동시에 개선하기 위해 다양한 후속 연구들이 진행되었고, 현재 Mip-NeRF360이 이미지 품질 면에서 최첨단 기술로 자리 잡고 있습니다. 하지만 이 방법은 여전히 훈련과 렌더링 시간이 매우 길다는 단점이 있습니다.

최근 방법들은 주로 빠른 훈련 또는 렌더링을 목표로 하며, 공간 데이터 구조를 사용해 Volumetric Ray-Marching중에 신경 특징(neural features)을 보간하거나, 다양한 인코딩 및 MLP 용량을 활용하는 방법을 사용합니다. 예를 들어, InstantNGP는 hash grid와 Occupancy Grid를 사용해 계산을 가속하고, 작은 MLP로 밀도와 외관을 표현합니다. Plenoxels는 희소한 Voxel Grid를 사용해 연속적인 밀도 필드를 보간하며, 신경망 없이도 작동할 수 있습니다.

• 한계점:
  • 위의 방법들은 훌륭한 결과를 제공하지만, 빈 공간(empty space)을 효과적으로 표현하는 데 어려움을 겪을 수 있으며, 구조화된 그리드의 선택이 이미지 품질에 큰 영향을 미칩니다. 또한, 레이 마칭 단계에서 많은 샘플을 쿼리해야 하기 때문에 렌더링 속도가 저하될 수 있습니다.
  • 이 논문에서 제안하는 Unstructured, Explicit, GPU-Friendly 3D Gaussians는 이러한 문제를 극복하며, 신경망을 사용하지 않고도 빠른 렌더링 속도와 더 나은 품질을 제공합니다.

Point-Based Rendering and Radiance Fields

Point-Based Rendering

• Point-based rendering은 연결되지 않은 비구조적인 기하학 샘플(예: point clouds)을 효율적으로 렌더링하는 방법입니다. 가장 단순한 형태에서는 고정된 크기의 포인트를 래스터화하여 렌더링하지만, 이러한 방식은 구멍이 생기거나 Aliasing(왜곡)이 발생할 수 있으며, 기본적으로 비연속적입니다.
• 이를 해결하기 위해 포인트 기반 렌더링에서 포인트를 픽셀보다 큰 원이나 타원 등의 형태로 Splatting하여 더 나은 품질을 제공하는 방법들이 제안되었습니다.
• 최근에는 Differentiable Point-Based Rendering 기술들이 등장하여 포인트에 신경망 기능을 추가하고 CNN을 사용해 렌더링을 수행함으로써 빠른 시점 합성을 가능하게 했습니다. 그러나 이러한 방법들은 여전히 초기 기하학을 위해 MVS를 필요로 하며, 이로 인해 발생하는 과잉 재구성 또는 부족한 재구성과 같은 아티팩트를 피할 수 없습니다.

Radiance Fields

• NeRF와 Point-based α-blending 방식은 사실상 동일한 이미지 생성 모델을 공유합니다. NeRF는 연속적인 표현 방식을 사용하여 공간의 비어 있는 부분과 채워진 부분을 암묵적으로 표현하며, Volumetric Ray-Marching은 비용이 많이 드는 무작위 샘플링이 필요합니다.
• 반면, Point-based 방식은 비구조적이고 불연속적인 표현 방식으로, 기하학의 생성, 파괴, 변위를 허용하는 유연한 접근법입니다. 예를 들어, Pulsar는 빠른 구체 래스터화를 달성하며, 제안된 방법은 이를 기반으로 한 타일 기반과 정렬된 렌더링 알고리즘을 사용하여 시각적 품질을 개선합니다.

Rendering Methodology

• NeRF 방식과 비교하여, 제안된 방법은 렌더링 속도와 품질을 모두 향상시킵니다. Pulsar와 같은 이전 방법들은 신경망을 사용한 렌더링 때문에 Temporal Instability(시간적 불안정성)을 겪지만, 제안된 방법은 이 문제를 극복하면서 더 빠르고 안정적인 렌더링을 제공합니다.
• 또한, 제안된 방법은 3D Gaussians를 사용하여 더 유연한 장면 표현을 제공하며, MVS 기하학을 사용할 필요 없이 복잡한 장면을 다룰 수 있는 이점을 가지고 있습니다.

결론적으로 제안된 방법은 3D Gaussians를 사용하여 Point-Based Rendering의 효율성을 가져오면서도, Radiance Fields의 연속적인 장면 표현의 장점도 활용합니다.

Overview

전반적인 모델의 아키텍처와 수도 코드를 통해서 모델의 작동원리를 설명해드리겠습니다. 이에 대한 자세한 설명은 아래에 적어두었으니 참고하시길 바랍니다.

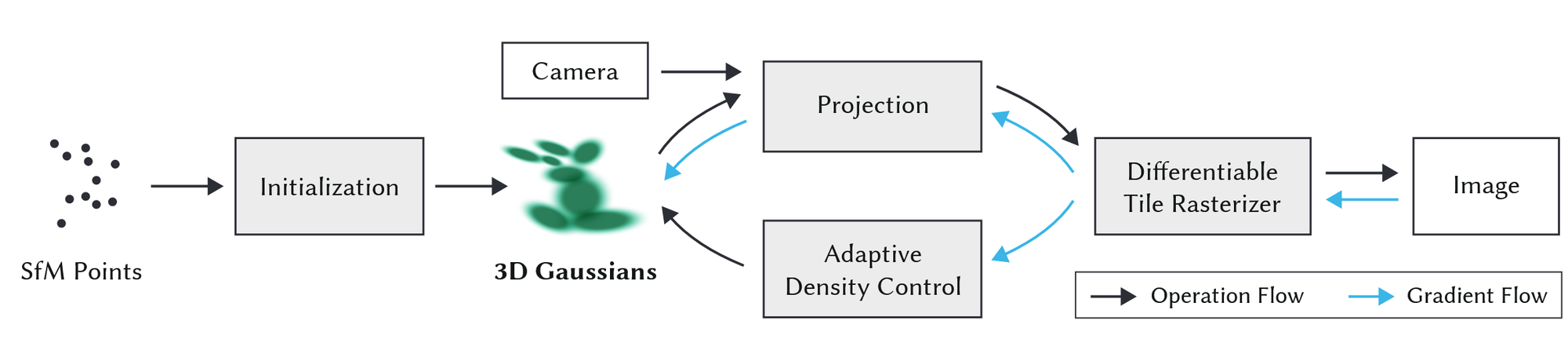
입력값: 여러가지 시점에서 찍은 static한 이미지와 해당 이미치의 camera pose 정보

→ 위의 입력값을 SfM을 이용해 spare point cloud로 변경합니다.

Initialization: spare point cloud의 값들에 대해서 3D Gaussian 값을 생성

• 각 3D Gaussian은 위치(평균), 공분산 행렬(방향성과 모양을 나타냄), 그리고 불투명도(α)로 정의

Radiance Field의 색상 표현

• Radiance Field의 방향성 색상 요소는 Spherical Harmonics (SH)를 사용하여 표현됩니다. SH는 3D 장면에서 특정 방향에 따라 색상 변화를 표현하는 데 적합합니다.

• 알고리즘은 3D Gaussian 파라미터(위치, 공분산, α, SH 계수)를 최적화하면서 방사 필드 표현을 생성합니다.

• 제안된 방법의 핵심은 타일 기반 래스터라이저입니다. 이 래스터라이저는 α-blending을 사용하여 anisotropic splats를 처리하면서 가시성 순서를 고려합니다.

M ← SfM Points

SfM을 통해서 초기의 Sparse Point Clou 데이터를 M에 할당해줍니다.

S, C, A ← InitAttributes()
Gaussian의 초기 속성값을 초기화하는 함수입니다. S는 Gaussian의 위치, C는 공분산과 색상, A는 불투명도(alpha)를 나타냅니다.

while not converged do
알고리즘이 수렴할 때까지 반복문을 실행합니다.

V, Î ← SampleTrainingView()
현재의 카메라 위치 V와 해당 위치에서 보이는 실제 이미지를 샘플링합니다. Î는 이 샘플링된 이미지입니다.

I ← Rasterize(M, S, C, A, V)
주어진 카메라 위치 V에서 3D Gaussian을 사용하여 이미지를 렌더링합니다. M, S, C, A는 Gaussian의 속성입니다.

L ← Loss(I, Î)
렌더링된 이미지 I와 실제 이미지 Î 간의 손실(Loss)을 계산합니다.

M, S, C, A ← Adam(∇L)

손실 L에 대한 그래디언트를 계산하고, Adam 옵티마이저를 사용하여 Gaussian의 속성 (M, S, C, A)을 업데이트합니다.

if IsRefinementIteration(i) then

i가 특정 조건을 만족하는지 확인하여, Gaussian의 밀도 조정 및 최적화 과정인 Refinement 단계를 진행할지 결정합니다.

for all Gaussians (μ, Σ, c, α) in (M, S, C, A) do

현재 존재하는 모든 Gaussian에 대해 반복문을 실행합니다. 여기서 μ는 Gaussian의 평균(위치), Σ는 공분산, c는 색상, α는 불투명도를 나타냅니다.

if α < ε or IsTooLarge(μ, Σ) then

Gaussian의 불투명도 α가 임계값 ε보다 작은지, 또는 Gaussian의 크기가 너무 큰지 확인합니다.

RemoveGaussian()
위의 조건에 의해 선택된 Gaussain을 제거

if ∇pL > τp then

Gaussian의 위치에 대한 손실 함수의 그래디언트(∇pL)가 임계값(τp)보다 큰지 확인합니다. 이 조건이 참일 경우 Gaussian의 밀도를 조정합니다.

if ‖S‖ > τS then

Gaussian의 크기 S가 임계값 τS보다 큰지 확인합니다. 크기가 너무 크다면, Gaussian을 분할하여 밀도를 조정합니다.

SplitGaussian(μ, Σ, c, α)

Gaussian을 분할하여 두 개의 더 작은 Gaussian을 생성합니다. 이는 과도한 재구성(Over-reconstruction)을 방지하기 위한 조치입니다.

CloneGaussian(μ, Σ, c, α)

크기가 너무 크지 않다면 Gaussian을 복제하여 밀도를 높입니다. 이는 미구성(Under-reconstruction)을 방지하기 위한 조치입니다.

DIFFERENTIABLE 3D GAUSSIAN SPLATTING

3D Gaussians을 선택한 이유는 미분가능하고, 2D로 projection이 용이하고, 빠른 a-blending 렌더링을 가능하게 합니다.

SfM 포인트 클라우드는 매우 Sparse하기 때문에 Normal을 추정하는 것이 어렵습니다. 또한, 추정된 Normal 값이 매우 노이즈가 많아 최적화가 어렵습니다. 이에 따라, Normal을 추정하지 않고 3D Gaussians를 사용하여 기하학을 표현합니다. 이러한 Gaussians는 월드 좌표계에서 정의된 전체 3D 공분산 행렬 Σ으로 정의됩니다.

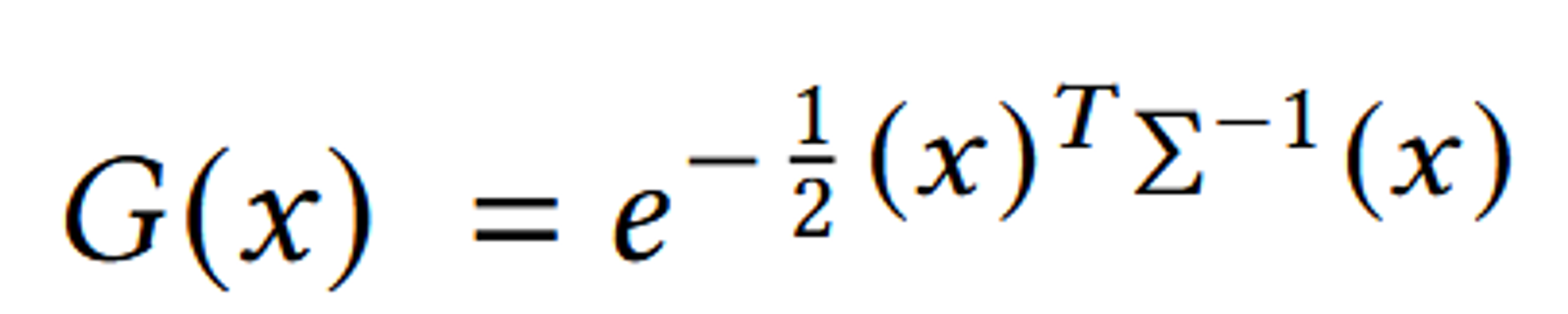
3D Gaussian은 위와 같은 형태로 정의됩니다.

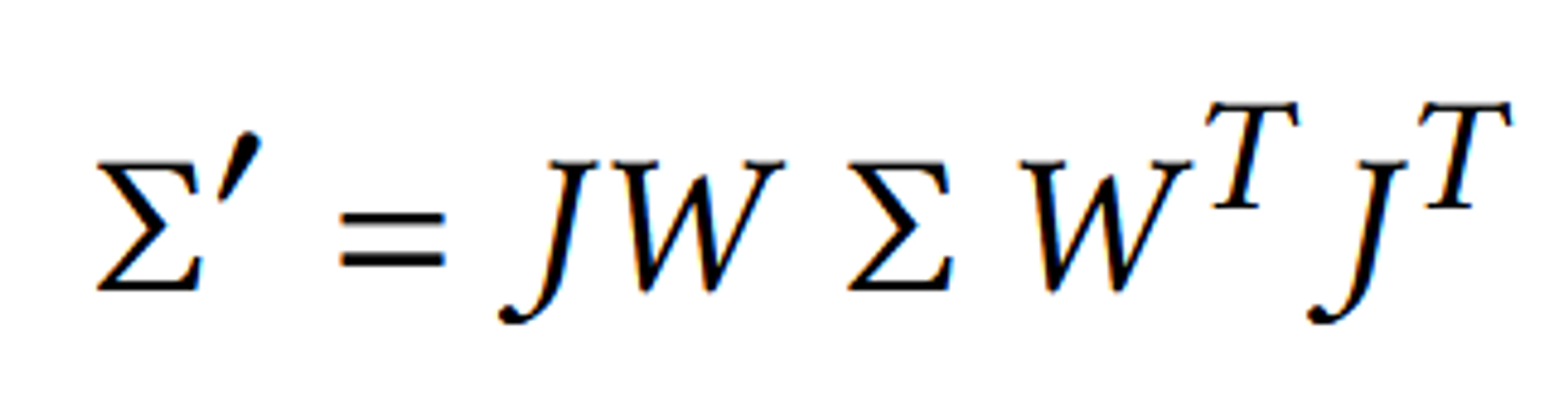
3D Gaussian을 2D로 Projection 시키는 식은 위와 같습니다.

• Σ′: 이는 변환된 공분산 행렬로, 카메라 좌표계에서 표현된 공분산 행렬입니다. 즉, 원래 3D 공간에 정의된 Gaussian을 2D 이미지 평면으로 투영한 후의 공분산 행렬입니다.
• J: 이 행렬은 Jacobian 행렬로, 투영 변환의 미분을 나타냅니다. 투영된 좌표와 원래 좌표 사이의 선형 근사를 표현하며, 투영된 2D 공간에서의 미세한 변화를 반영합니다.
• W: Viewing transformation을 나타내는 행렬입니다. 이는 월드 좌표계에서 카메라 좌표계로의 변환을 나타내며, 3D 공간에 위치한 점들이 카메라 좌표계에서 어떻게 보일지를 결정합니다.
• Σ: 원래의 3D 공간에서의 공분산 행렬입니다.

원래는 3x3 matrix이지만 2차원으로 매핑하기때문에 3번째 열과 행의 정보를 제거하고 2x2 matrix로 나타낼 수 있습니다.

공분산 행렬 Σ와 Positive Semi-Definiteness

• 공분산 행렬 Σ: 3D Gaussian의 공분산 행렬 Σ는 해당 Gaussian의 형태와 크기, 방향성을 정의하는 중요한 요소입니다. 그러나, 이 행렬이 물리적으로 의미를 가지기 위해서는 positive semi-definite여야 합니다. 이는 행렬의 모든 고유값이 0 또는 양수여야 함을 의미합니다. 만약 Σ가 positive semi-definite가 아니라면, Gaussian의 형태가 왜곡되거나 물리적으로 의미가 없는 상태가 됩니다.
• 문제점: 그러나, Gradient Descent와 같은 최적화 기법을 사용할 때, 이러한 positive semi-definite을 유지하는 것은 어려운 과제입니다. 최적화 과정에서의 업데이트가 유효하지 않은 공분산 행렬을 생성할 수 있기 때문입니다. 이는 최적화 도중에 Σ가 물리적으로 타당하지 않은 상태가 될 수 있다는 문제점을 초래합니다.

대안적인 표현: Scaling Matrix S와 Rotation Matrix R

• 대안적 접근: 위 문제를 해결하기 위해 저자들은 공분산 행렬 Σ를 직접적으로 최적화하는 대신, 이를 S와 R을 이용해 표현하는 방법을 선택했습니다. Σ를 표현할 때, 스케일링 행렬 S와 회전 행렬 R을 사용하여 이를 구성할 수 있습니다. 즉, 공분산 행렬 Σ는 아래와 같이 표현됩니다:

  

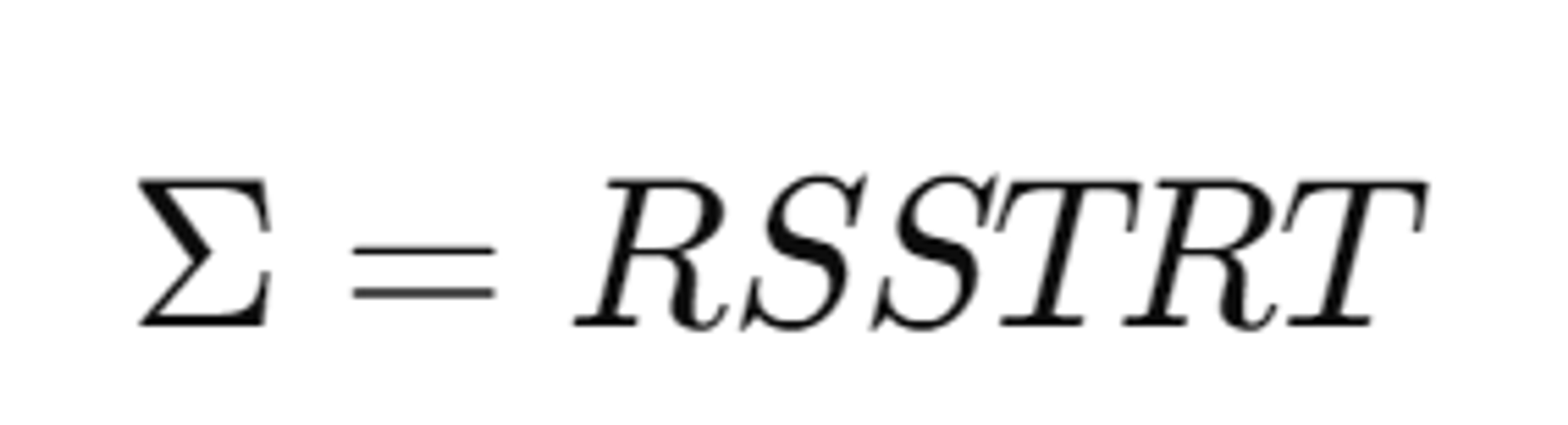
  • S는 3D 벡터 s로 표현된 스케일링(크기) 행렬입니다.
  • R는 회전을 나타내는 행렬로, quaternion q를 사용하여 표현됩니다.

• 이점: 이 방법은 Σ를 양의 준정부호로 유지하면서도 최적화할 수 있는 효율적인 방법입니다. 또한, 스케일링과 회전을 독립적으로 최적화할 수 있기 때문에, 각각의 요소에 대해 보다 직관적인 조정을 할 수 있습니다.

Optimization

렌더링 결과를 캡처된 데이터셋의 훈련 뷰와 비교하여 최적화합니다. 이 과정에서 잘못된 기하학적 위치를 수정할 수 있어야 하며, 잘못 배치된 기하학적 요소를 생성, 제거 또는 이동할 수 있어야 합니다.

부가적인 요소들

• SGD(Stochastic Gradient Descent) 방식의 사용
• fast rasterization
• a(aplha blending)에 sigmoid를 적용시켜 [0-1)까지의 값을 갖고, smooth gradients를 갖도록 합니다.
• 초기 공분산 행렬은 등방성(isotropic) Gaussian으로 설정됩니다.
• exponential decay scheduling

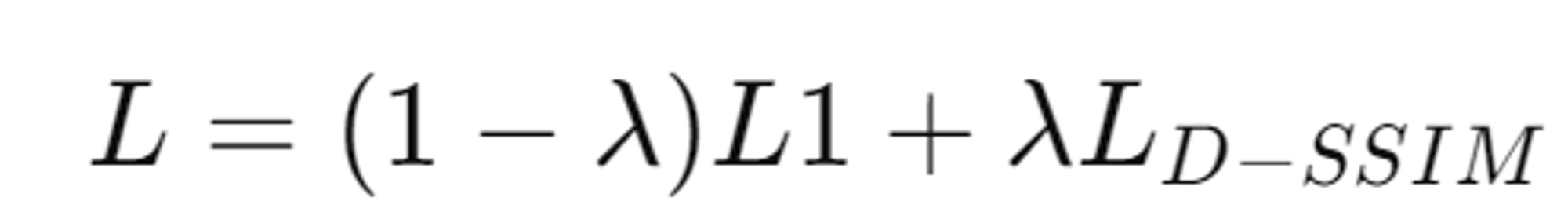
L1 Loss: 예측된 값과 실제 값 간의 절대적인 차이를 최소화 (λ = 0.2)

D-SSIM Loss: 구조적 유사성을 고려하여 더 정교한 이미지 품질을 보장합니다.

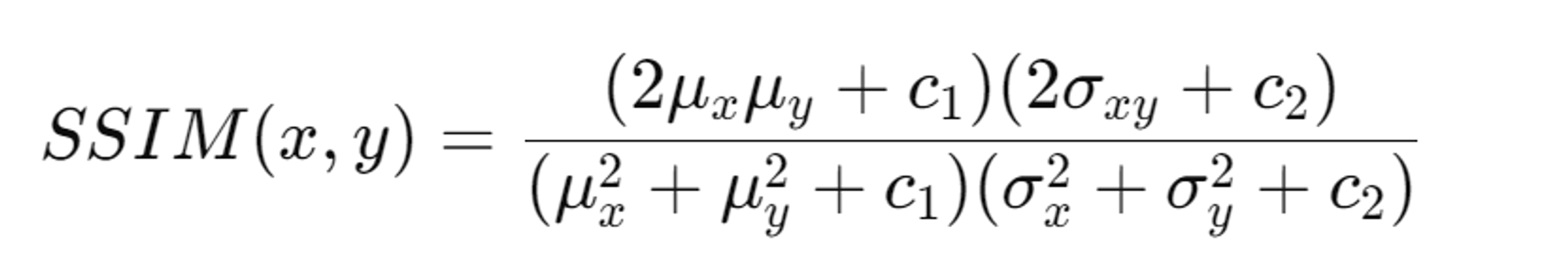
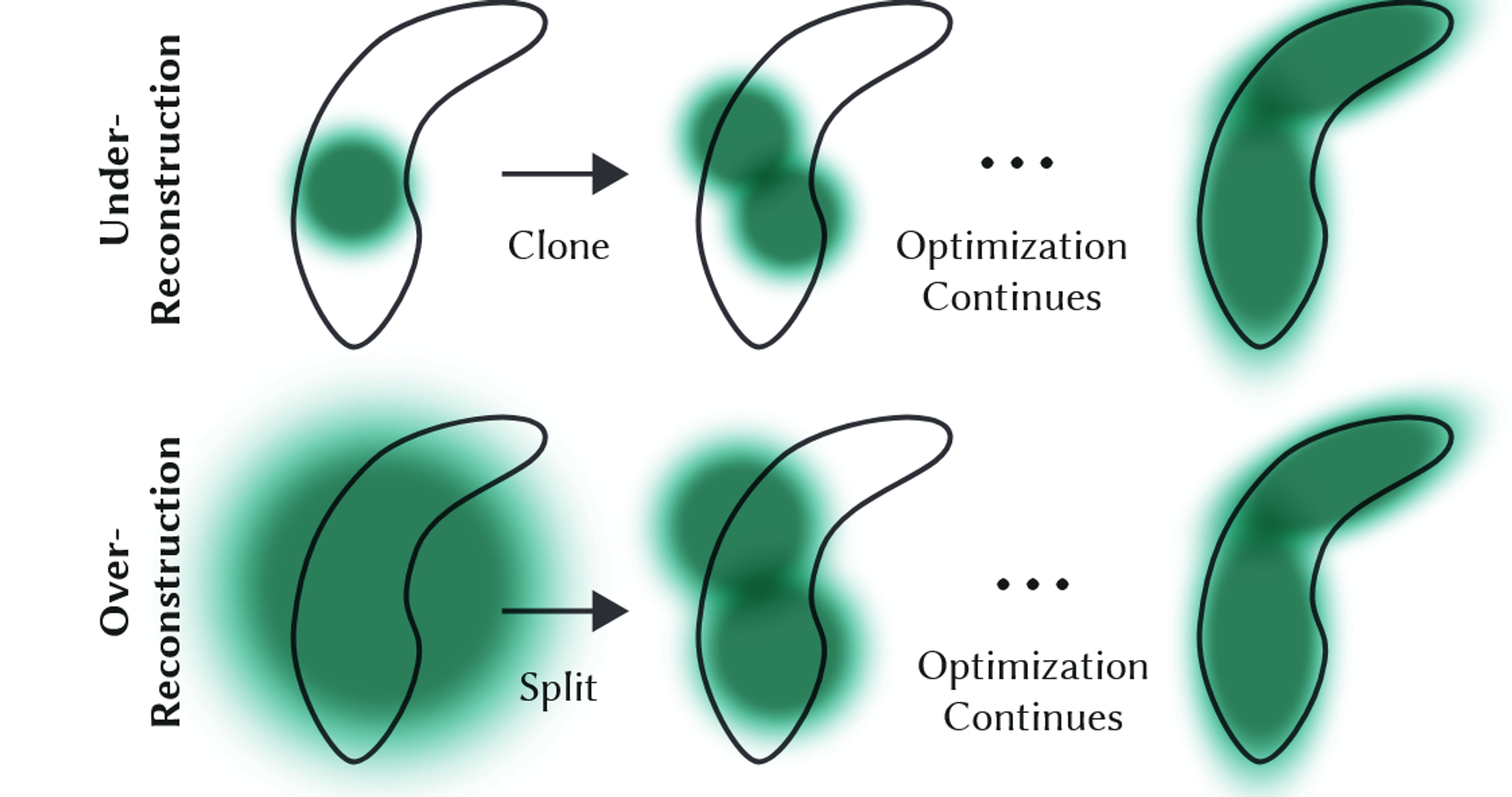
Adaptive Control of Gaussians

• 초기 Sparse Gaussian 집합:
  • SfM에서 제공하는 Sparse Point Clouds로 시작합니다.
  • 이 Point Clouds를 바탕으로 초기의 Sparse한 3D Gaussian을 생성합니다.
• Adaptive Control:
  • Gaussian의 수와 장면 내에서의 밀도를 동적으로 조절합니다.
  • 100번의 최적화 반복마다, 투명도가 특정 임계값 이하인 Gaussian은 제거하고, 새롭게 필요한 부분에 Gaussian을 추가하여 밀도를 높입니다.
• Under-reconstruction과 Over-reconstruction:
  • 장면의 일부가 Under-reconstruction된 경우(즉, 충분한 정보가 없거나, 잘못된 위치에 정보가 있는 경우), 이 부분을 Gaussian으로 채우도록 합니다.
  • 반대로, Over-reconstruction된 경우(즉, 너무 많은 Gaussian이 필요 이상으로 큰 영역을 차지하는 경우), 이 영역의 Gaussian을 분할하여 더 작은 Gaussian으로 교체합니다.
• 밀도 제어 방법:
  • Gaussian이 Under-reconstruction 부분에서는 Gaussian을 복제하고, 복제된 Gaussian을 위치 변화에 따라 이동시켜 새로운 형상을 덮도록 합니다.
  • Over-reconstruction된 Gaussian은 더 작은 두 개의 Gaussian으로 분할하고, 크기를 축소하여 원래의 3D Gaussian을 확률 밀도 함수(PDF)로 사용해 새로운 위치에 Gaussian을 생성합니다.
  • 이러한 방식으로 Gaussian의 총 볼륨을 유지하면서 필요한 곳에 밀도를 집중시킵니다.
• Floaters 처리:
  • 최적화 과정에서 Gaussian이 입력 카메라 근처에 Floatsers 문제가 발생할 수 있습니다.
  • 이러한 문제를 해결하기 위해, 특정 횟수의 반복 후에 α 값을 거의 0에 가깝게 설정한 다음, 필요한 Gaussian만 α 값을 다시 높이도록 합니다.
  • 이로 인해 부적절하게 생성된 Gaussian은 제거되고, 필요한 부분에만 Gaussian이 집중되도록 합니다.
• Gaussian의 주기적인 제거:
  • 매우 큰 Gaussian이나 장면에서 큰 영향을 미치는 Gaussian은 주기적으로 제거하여 전체 Gaussian의 수와 밀도를 적절히 유지합니다.
  • 이 방법은 다른 방법들에서 사용하는 공간 압축, 왜곡, 또는 투영 전략 없이도 Euclidean 공간 내에서 Gaussian을 유지하며 효과적으로 작동합니다.

FAST DIFFERENTIABLE RASTERIZER FOR GAUSSIANS

• 렌더링과 정렬 최적화:
  • 이 방법은 빠른 렌더링과 빠른 정렬을 목표로 하여 α-blending을 수행합니다.
  • 타일 기반의 래스터라이저를 설계하여 화면을 16×16 크기의 타일로 나누고, 각 타일에 대해 렌더링을 수행합니다.
• 타일별 처리:
  • 화면을 16×16 크기의 타일로 나누고, 각 타일에 대해 3D Gaussians를 걸러냅니다. 이 과정에서 view frustum와 교차하는 3D Gaussian만 남기고, 나머지는 제외합니다.
  • 각 타일에서 3D Gaussian들을 빠르게 정렬하기 위해 GPU Radix sort를 사용하여 정렬을 수행합니다.
• α-blending 및 병렬 처리:
  • 각 타일에 대해 스레드 블록을 실행하여 타일 내에서 색상과 α 값을 누적합니다.
  • 목표 α 포화 상태에 도달하면 해당 스레드는 처리를 중지하고, 전체 타일의 모든 픽셀이 포화 상태에 도달하면 타일 처리를 종료합니다.
• 메모리 효율성 및 그래디언트 계산:
  • 이 방법은 특정 타일에서 α 포화만을 중지 조건으로 사용하며, 이전 작업들과 달리 블렌딩된 primitive에 대해 그래디언트 업데이트를 받을 수 있는 개수를 제한하지 않습니다.
  • 역방향 패스에서는, 전체 블렌딩된 점들의 순서를 복구해야 합니다. 이를 위해 각 픽셀에 대해 중간 불투명도를 저장하지 않고, 최종 누적 불투명도만 저장한 후 이를 기반으로 역방향 패스에서 필요한 계수를 계산합니다.

CullGaussian(p, V)

주어진 카메라 뷰 구성 V에 따라 시야각 프러스텀 내에 위치하지 않은 3D Gaussians를 제거

M', S' ← ScreenspaceGaussians(M, S, V)

3D 공간에 있는 Gaussians의 위치 및 공분산 행렬을 2D 스크린 공간으로 변환합니다.

T ← CreateTiles(w, h)

스크린 공간을 w x h 크기의 타일로 분할합니다. 이 타일링 과정은 병렬 처리를 가능하게 하고, GPU에서의 효율적인 계산을 위해 사용됩니다.

L, K ← DuplicateWithKeys(M', T)

타일 T와 중복되는 Gaussians를 인덱싱하고, 각 Gaussian에 대해 깊이 값과 타일 ID를 포함한 키를 생성합니다. 이 키는 나중에 정렬 과정에서 사용됩니다.

SortByKeys(K, L)
위에서 생성한 키 K에 따라 Gaussians를 정렬합니다. 이 단계에서 동일한 타일 내의 Gaussians가 깊이 순서로 정렬됩니다.

R ← IdentifyTileRanges(T, K)

각 타일에 대해 정렬된 Gaussian 목록에서 첫 번째 및 마지막 Gaussian의 인덱스를 식별합니다. 이 정보를 사용해 각 타일에 대해 필요한 Gaussian들을 가져옵니다.

for all Tiles t in I do
모든 타일 t에 대해 루프를 실행합니다. 이 과정은 병렬 처리를 위한 것이며, 각 타일에 대해 별도로 작업을 수행합니다.

for all Pixels i in t do
각 타일 t 내의 모든 픽셀 i에 대해 루프를 실행합니다.

r ← GetTileRange(R, t)

현재 타일 t에 대한 Gaussian들의 범위를 가져옵니다. 이 단계에서 타일 t에 대한 Gaussian들의 범위를 결정하여 해당 타일에 대해 적절한 Gaussian들을 가져옵니다.

I[i] ← BlendInOrder(i, L, r, K, M', S', C, A)
해당 픽셀 i에 대해 Gaussian들을 깊이 순서대로 혼합하여 최종 색상을 계산합니다.

IMPLEMENTATION, RESULTS AND EVALUATION

자세한 내용은 추후에 업데이트 하도록 하겠습니다.