Mip-NeRF 360 논문리뷰

이한결·2024년 8월 14일

논문 링크

https://arxiv.org/abs/2111.12077

Abstract

NeRF가 view synthesis에서 좋은 결과를 냈지만, 경계가 없는 무한한 공간인 unbounded scene의 경우에서는 좋지 않은 결과를 냈다.

이전의 NeRF 기반 모델들은 blurry하거나 low-resolusion rendering을 생성한다.

해당 논문에서는 mip-NeRF를 기반으로 non-linear scene parametrization, online distillation, novel distortion-based regularizer를 사용했다.

왼쪽사진이 mip-NeRF, 오른쪽 사진이 mip-NeRF 360 모델이다. mip-NeRF의 전체사진옆에 crop된 이미지들을 자세히 보면 배경들이 흐릿하게 나온 부분이 많다. 이에 비해 해당 논문의 mip-NeRF 360 모델은 뒤의 배경까지 잘 잡아내어 평가지표 SSIM이 mip-NeRF보다 월등히 높은 것을 알 수 있다.

기존 NeRF 기반 모델들의 한계

Parameterization:

유한한 경계 내에서만 3D 좌표를 처리할 수 있어, 매우 큰 공간이나 무한히 확장된 장면을 다루기 어렵다.
cf. parameterization은 공간의 각 점을 특정 좌표 체계로 표현하는 방법

Efficiency:

큰 네트워크 용량이 필요하며, 각 광선을 따라 밀집하게 쿼리하는 것은 계산 비용이 많이 든다. 이는 대규모 장면을 효율적으로 처리하기 어렵게 만든다.

Ambiguity:

제한된 수의 광선으로 관찰된 객체는 다양한 거리에서 나타날 수 있어, 3D 장면을 정확하게 재구성하는 데 어려움을 겪는다.

NDC

위의 한계들의 극복 방법을 설명하기전에 NDC 방법에 대해서 확실하게 설명하고 넘어가도록 하겠다. NeRF에서 사용한 방식인데 이 논문에서 자주 사용되는 개념이기 때문이다.

NDC는 3가지 역할을 진행한다

Projection(3D 좌표 → 2D 좌표)

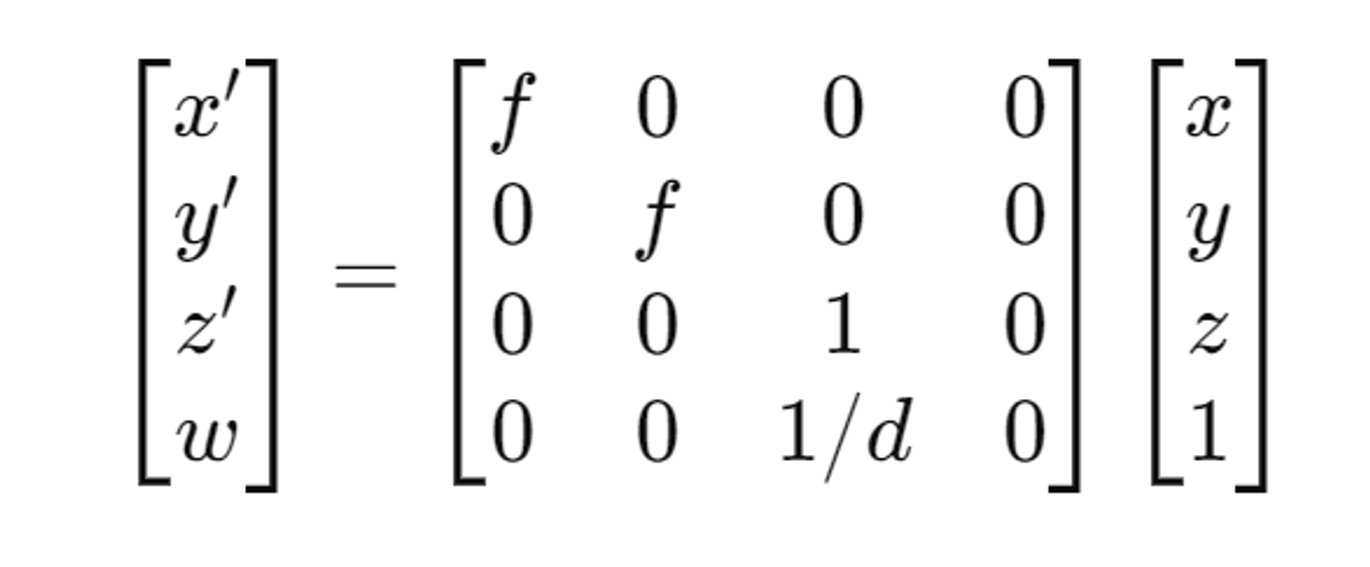
f는 초점 거리(focal length), d는 카메라에서의 깊이

정규화 [-1,1] & 3. 원근법 적용

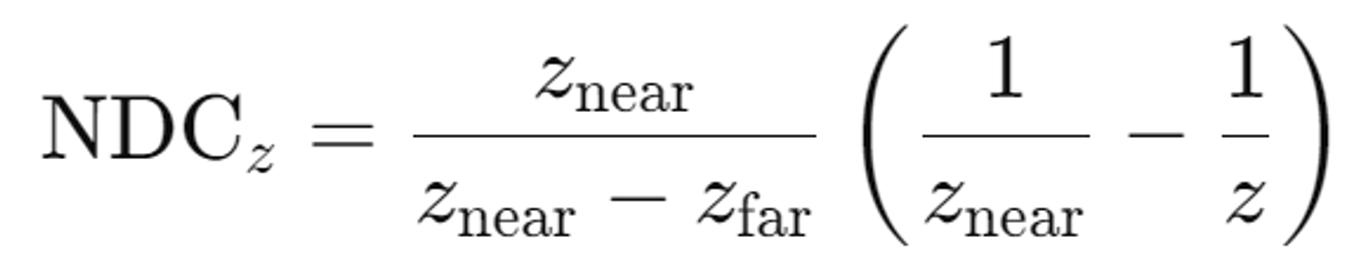
위의 한계들의 극복 방법

Parameterization

NeRF모델에서는 3D좌표를 2D 좌표로 변환한 후 NDC를 이용해서 효율적으로 정규화 했다.

z축 방향으로 너무 멀리 있는 물체들은 NDC 방식에서 적절히 표현되지 않을 수 있다. 예를 들어, 무한히 먼 거리에 있는 물체는 NDC 방식에서 잘려나가거나 왜곡될 수 있다.

NDC 방식이 z축을 기준으로 한 원근 투영을 다루는 데에는 적합하지만, unbounded scenes을 다루기 위해서는 새로운 파라미터화 방법이 필요하다.

Efficiency

Unbounded scene은 복잡하고 크기 때문에 기존 NeRF 모델의 용량이 한계에 도달하고, 더 많은 학습시간을 필요로 한다.

NeRF에서 사용하는 계층 학습 방법(coarse, fine network)는 2번 학습을 진행하기 때문에 계산의 비효율성이 있다고 언급했다.

이에 해당 논문에서는 proposal MLP와 NeRF MLP로 변경했다.

proposal MLP는 밀도(density)를 측정하고, 해당 값을 통해서 새로운 간격(interval)을 resampling 하는데 사용된다. 해당 MLP는 학습되지 않고 NeRF MLP를 기반으로 가중치가 업데이트된다.

이에 따라 mip-NeRF보다 15배 큰 모델을 사용하지만 2배의 시간만 더 소요되도록 설계했다.

이러한 방법을 online distillation 접근법이라고 한다.

아래에서 다시한번 해당 내용들을 설명하겠다. 지금은 coarse, fine network대신에 proposal, MLP network를 사용했구나 정도만 알면될거같다.

Ambiguity

NeRF 모델이 기본적으로 새로운 뷰를 생성하는 데 있어underconstrained problem을 갖고 있다. underconstrained problem은 많은 입력 이미지를 사용하여 NeRF를 최적화할 때, 입력 이미지들을 설명할 수 있는 무한히 많은 NeRF 모델들이 존재하지만 이 중에서 새로운 각도에서 현실감 있는 이미지를 생성하는 모델은 소수에 불과하다는 것이다.

요약하면 NeRF모델은 많은 입력 이미지를 사용하여 장면을 최적화할 때, 새로운 각도에서 현실감 있는 이미지를 생성하기 위한 충분한 제약이 없다.

Scene and Ray Parameterizatio

mip-NeRF에서 unbounded scene을 처리하기 위해 Gaussian의 파라미터화를 어떻게 다시 설정하는지를 설명한다.

f(x)는 $R^n$ 에서 $R^n$ 으로 매핑하는 coordinate transformation 함수(n=3)

아래 나오는 Jacobian과 EKF 방식은 이전 방법으로서 그냥 간단히 읽고 넘어가도 되는 부분이다.

Jacobian

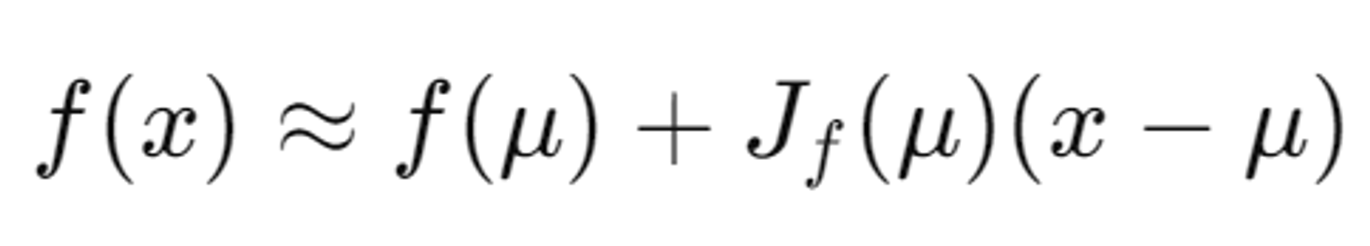
$J_f(μ)$ : μ에서의f의 Jacobian.이 식은 μ근처에서 f(x)를 선형으로 근사해준다.

Jacobian은 여러 개의 함수가 여러 개의 변수를 가지는 경우, 각 변수에 대한 함수의 변화율(미분)을 나타내는 행렬이다. 이는 여러 변수에 대한 함수의 변화를 나타내는 방법이다.

$f_1, f_2, \ldots, f_m$ 는 함수 f의 구성 요소
$x_1, x_2, \ldots, x_n$ 는 입력 변수

Extended Kalman Filter (EKF)는 비선형 시스템의 상태 추정을 위한 필터링 알고리즘

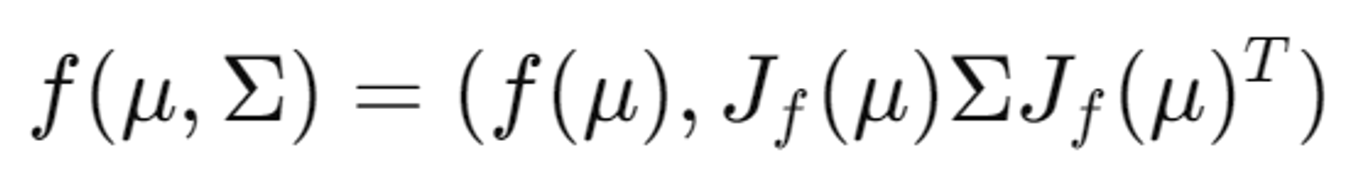
f(μ): 변환된 평균값
$J_f(\mu) \Sigma J_f(\mu)^T$ : 변환된 공분산 행렬
이는 Extended Kalman Filter와 기능적으로 동일

contract 함수

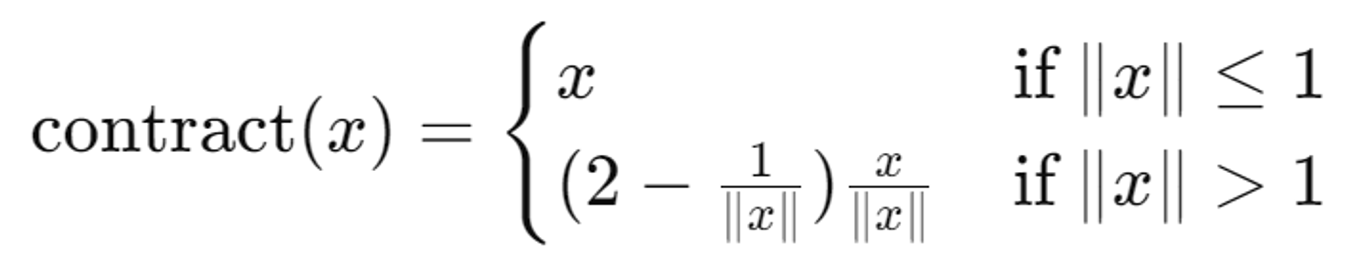
NDC와 같은 동기를 공유한다. 먼 점들을 거리 대신 반비례하는 disparity로 분포시키기 위해 설계한다. 이를 통해 원근 투영의 효과를 강조한다.

정리하자면 contract 함수는 기존의 Jacobian 및 EKF 기반 접근 방식을 대체하거나 보완하기 위해 사용된다.

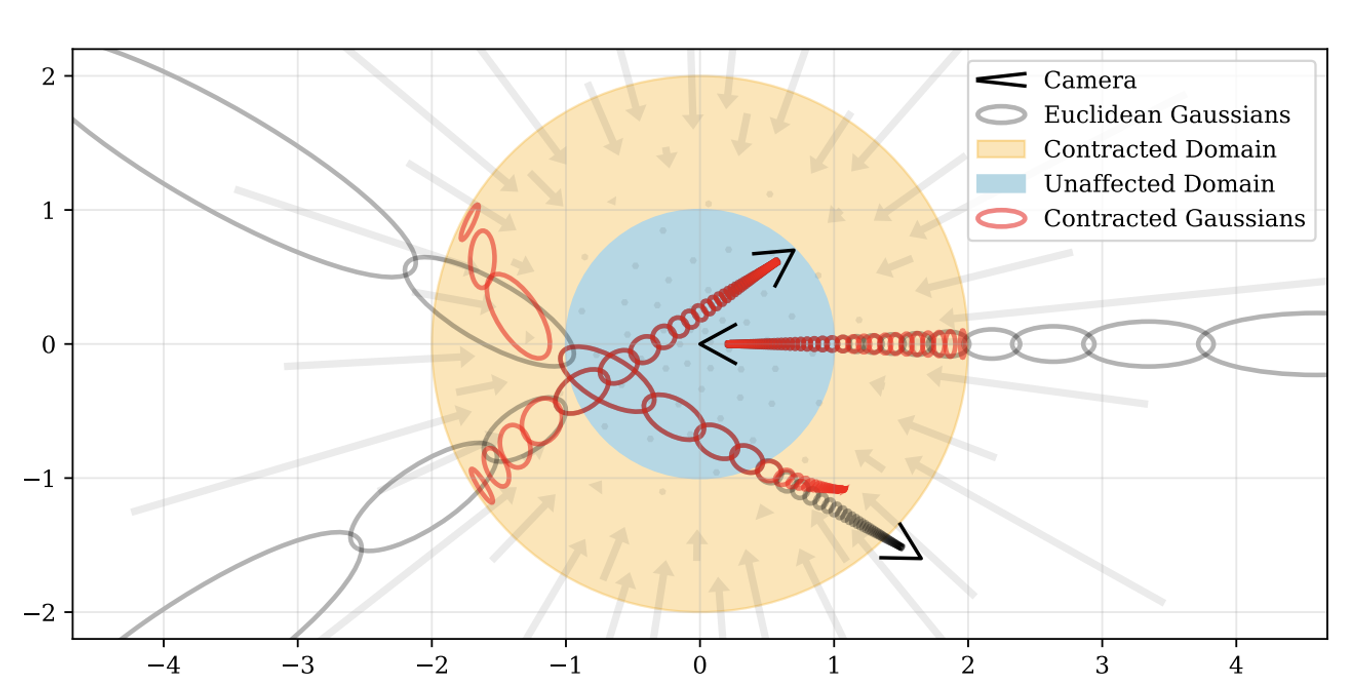
contract를 적용한 그림은 위와 같다. 실제로는 3D지만 시각화를 위해서 2D로 변환한 그림이다.

주황색 원: 반지름이 2인 contracted 영역을 나타낸다.

파란색 원: 반지름이 1인 contract 함수의 영향을 받지 않는 영역을 나타낸다.

회색타원: Gaussian을 적용한 유클리드 3D 공간

빨간타원: contract 함수를 적용한 후의 Gaussian 분포

noramalized ray distance s

NDC가 z축을 기준으로 작동하기 때문에 여러가지 방향에 대해서는 잘 작동하지 않는다. 이에 새로운 방법을 제시했다.

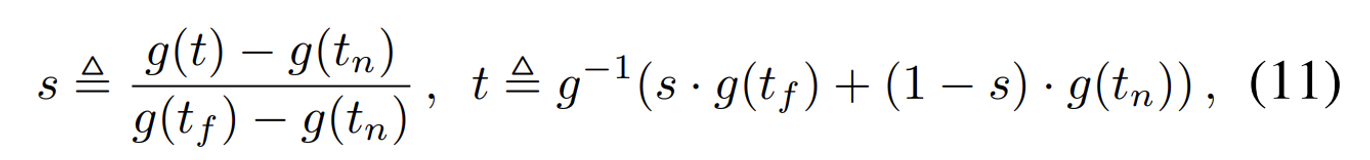
s의값은 s-space에 존재하고 t의 값은 t-space에 존재한다고 정의했다.

왼쪽 수식은 t에서 s space로의 변환이고, 오른쪽은 그의 반대다. 여기서 g(x)는 1/x를 나타낸다. 즉 깊이는 반비례하는 분포(disparity)로 변환된다. 이렇게 되면 멀리 있는 물체는 x가 크기때문에 분포 즉 물체의 크기는 작아지는 원근법이 적용된다.

기존에 NeRF나 Mip-NeRF에서는 t-space에서 샘플링을 진행했다면, 해당 논문에서는 s-space에서 샘플링을 진행했다. 이렇게 되면 깊이 값을 균등하게 분포시켜, 샘플링 과정에서의 불균형을 줄이고 무한히 확장된 장면에서도 균등한 샘플링을 가능하게 한다.

Coarse-to-Fine Online Distillation

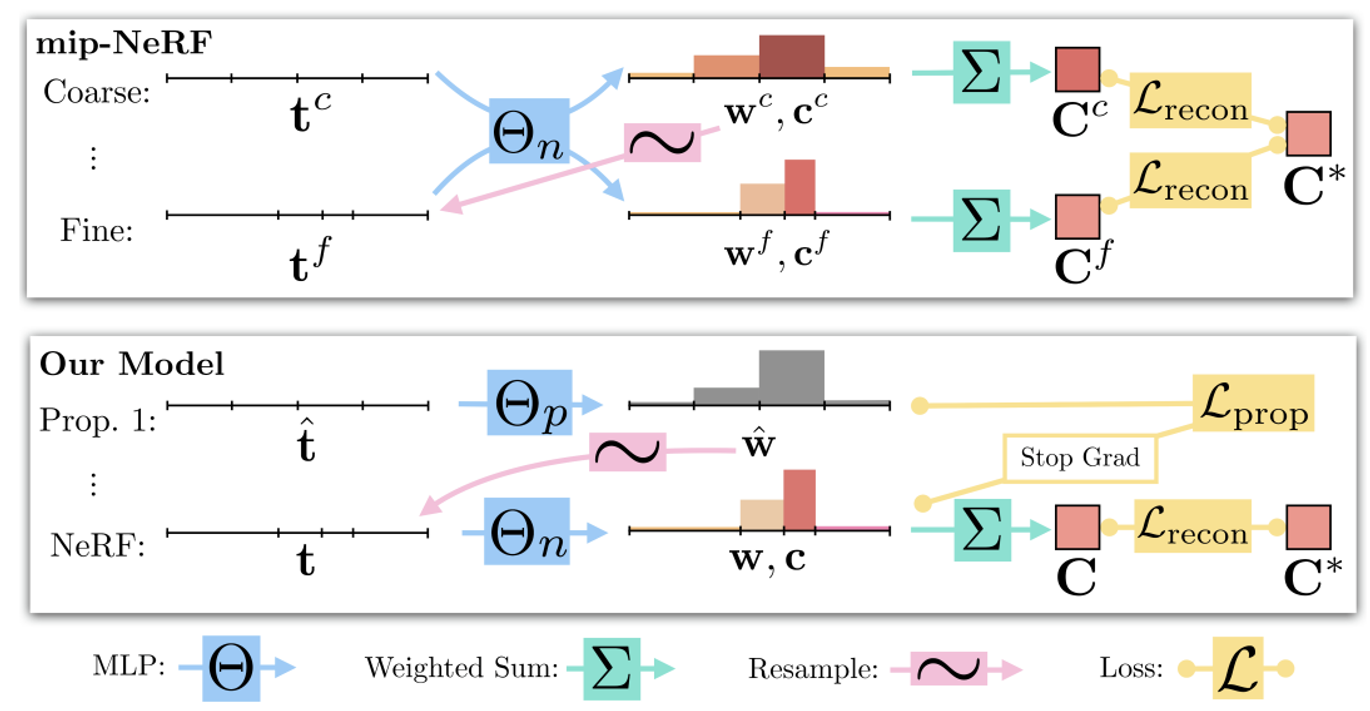
이전에 설명했던 것처럼 기존의 Coarse&Fine network가 아닌 Proposal&NeRF network를 사용하도록 수정했다.

2개의 MLP 모두 random 하게 initialize된다.

proposal MLP

s-space에서 샘플링된 점을 넣으면 color값 없이 volumetric density값과 해당 점에서의 weight값을 출력한다.

기존 Coarse&Fine 방식과 동일하게 해당 weight값을 기반으로 NeRF MLP의 입력 샘플들을 정한다. 이때 proposal MLP는 학습되지 않는다. 하지만 NeRF MLP의 weight 값의 bound를 이용해서 학습된다(아래에서 자세히 설명).

online distillation

작은 모델인 proposal MLP는 distillation 처럼 큰 모델의 NeRF MLP를 기반으로 학습된다. Proposal MLP는 장면의 중요한 부분을 더 잘 포착하려고 시도하며, NeRF MLP는 이를 기반으로 이미지를 생성한다. 이 두 MLP가 생성하는 히스토그램이 일관되도록 만드는 것이 중요하다. 여기서 히스토그램은 특정 거리(깊이)에서의 샘플링 빈도를 나타낸다.

proposal MLP가 학습이 잘 될 수록 장면의 중요한 부분이 샘플링 되고, 이렇게 되면 NeRF 샘플링 값은 이를 기반으로 만들어지기 때문에 장면의 중요한 부분에 더 집중된다. 따라서 2개의 샘플링 값은 서로 다른 bin 구조를 갖는다.

이를 해결하기 위해 전체적으로 일관된 샘플링을 유지하도록 loss 함수를 설계해야한다.

이때의 loss 함수의 최적의 값은 두 히스토그램이 동일한 분포를 반영하는 것이고, 동일한 분포가 아니라면 loss 값이 커야된다.

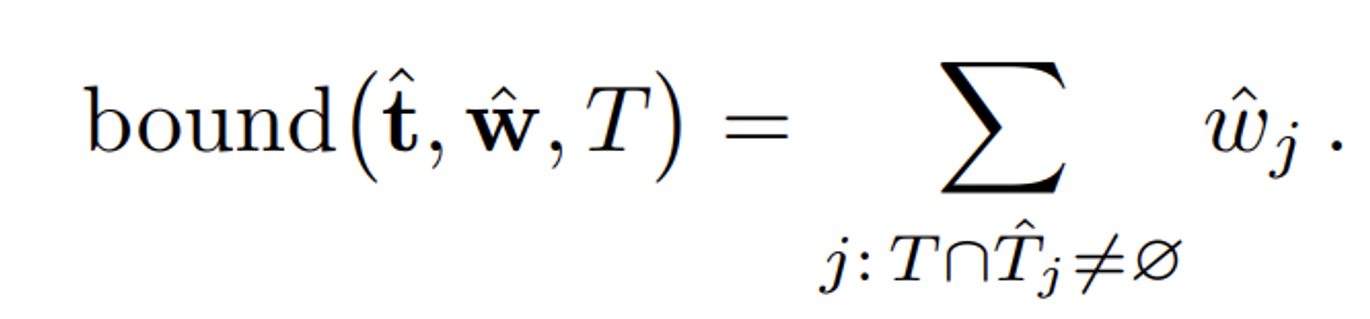
$\hat{t}$ : Proposal MLP가 예측한 샘플링 거리.
$\hat{w}$ : Proposal MLP가 예측한 가중치.
T: 특정 구간(interval).
$\hat{T}_j$ : Proposal MLP의 특정 구간.
$T \cap \hat{T}_j \neq \emptyset$ : 두 구간 T와 $\hat{T}_j$ 가 겹치는 경우.

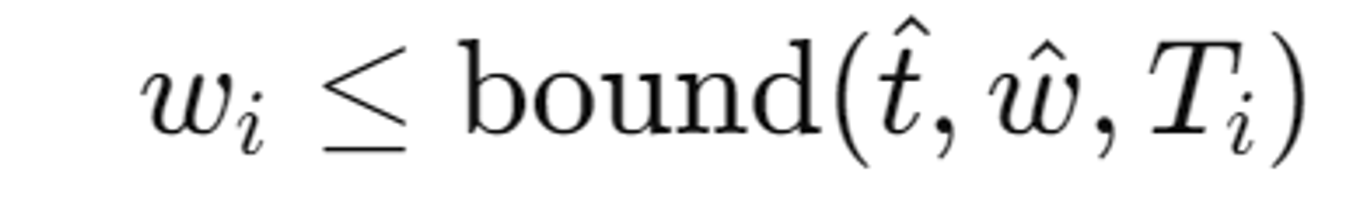
두 히스토그램이 일관성을 가지려면, NeRF MLP의 가중치 $w_i$ 가 bound을 초과하지 않아야 한다.

만약 NeRF MLP의 가중치 $w_i$ 가 Proposal MLP의 가중치 합산 값을 초과한다면, 이는 중요한 부분을 과도하게 샘플링하고 덜 중요한 부분을 충분히 샘플링하지 않는다는 것을 의미한다. 이렇게 되면 히스토그램의 일관성이 깨지게된다.

NeRF MLP

mip-NeRF에서 사용했던 $L_{recon}$ 을 그대로 사용한다. $L_{prop}$ 를 사용할 때는 sg(stop gradient)를 사용해서 학습이 되지 않도록 설정한다.

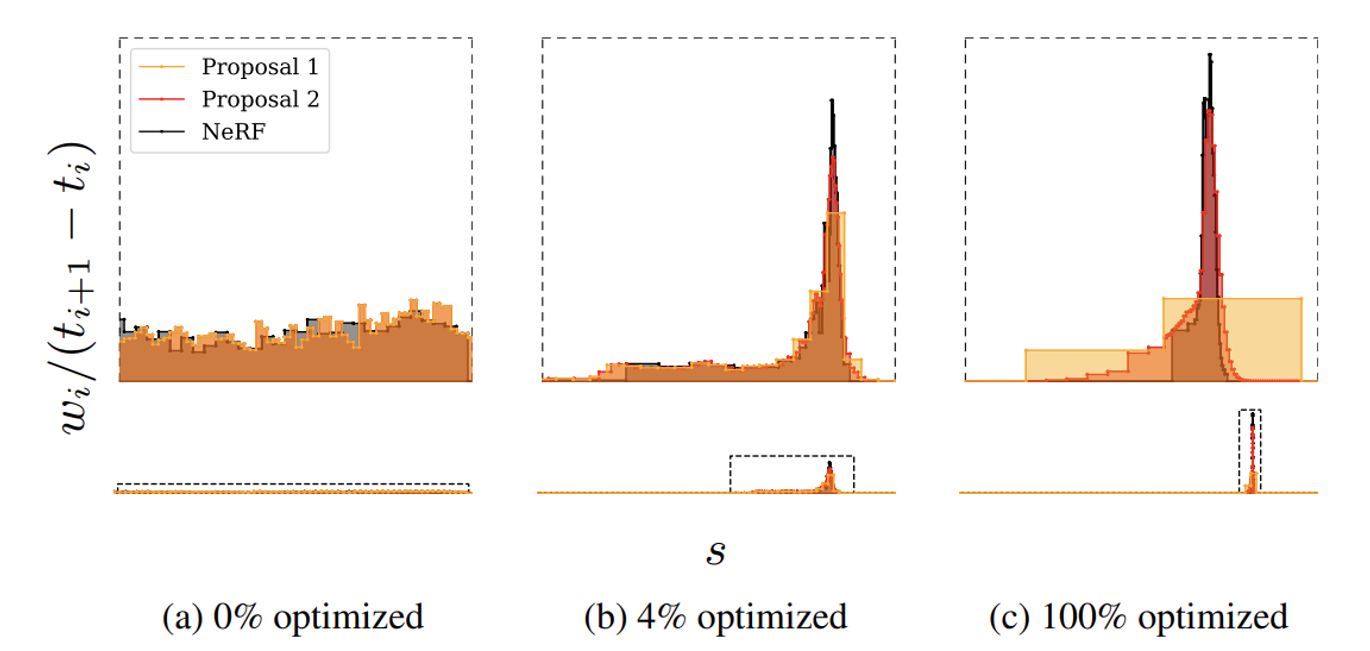
NeRF MLP의 (t,w) 히스토그램은 검정색, proposal MLP 2개의 히스토그램은 각각 노란색과 주황색이다.

(a): 처음 시작할 때 weight 값들은 uniformly distributed되어있다.

(b,c): 학습이 진행될수록 NeRF는 특정 구역(장면의 표면 주위)의 weight값이 증가하고 proposal network는 해당 히스토그램을 닮으면서 학습이 진행된다. 자세히 보면 proposal network가 NeRF network에 비해 조금 더 넓은 영역에 가중치를 분포시키는 것을 확인할 수 있다.

이를 통해 학습이 진행됨에 따라 NeRF MLP는 장면의 중요한 부분에 가중치를 집중시키고, Proposal MLP는 이러한 집중된 가중치를 포함하는 넓은 영역에 가중치를 분포시키는 것을 알 수 있다.

Regularization for Interval-Based Models

NeRF 모델을 학습하는 과정에서 두 가지 주된 문제점이 발생

"Floaters": 이는 공중에 떠다니는 것처럼 보이는, 연결되지 않은 Volume density가 높은 작은 영역을 의미한다. 이 영역들은 입력된 뷰의 일부 특성을 설명하기 위해 존재하지만, 다른 각도에서 보면 흐릿한 구름처럼 보이게 된다.
"Background collapse": 먼 거리에 있는 표면이 반투명한 밀도가 높은 구름으로 잘못 모델링되어 카메라에 가깝게 나타나는 현상입니다.

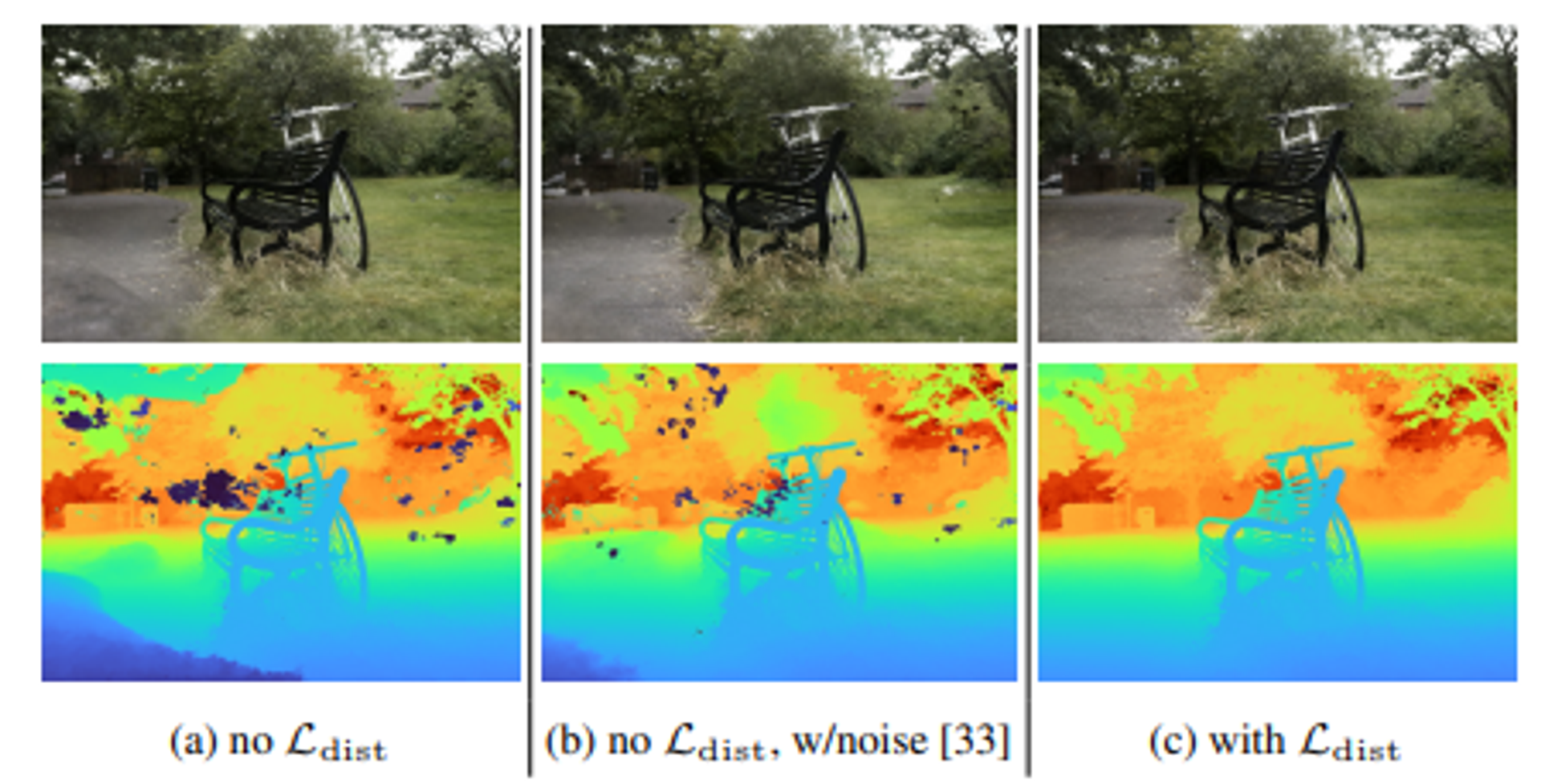
(a)사진을 통해서 floaters와 background collapse 현상을 볼 수 있습니다. 아래사진이 depth map을 나타내는데 그림 중앙과 주변에 검은색 또는 짙은 색으로 표현된 작은 점들이 보인다. 이는 특정 시점에서만 보이는 작은 반투명한 물체들이며, 이러한 물체들은 원래 존재하지 않거나 특정 시점에서만 보이는 잘못된 density 표현이다.

또한 depth map에서 배경들이 붉은색과 주황색의 물체들이 중첯ㅂ되면서 가까운 위치에 있는 것처럼 표현된 것을 볼 수 있다. 이는 원래 멀리 떨어져 있어야 할 배경 표면이 가까운 곳에 붕괴된 듯이 보이는 현상이다.

이를 방지하기 위해서 L_dist라는 새로운 정규화 손실을 제안했다.(아래 수식을 사용하기 때문에 생략가능)ㅁ

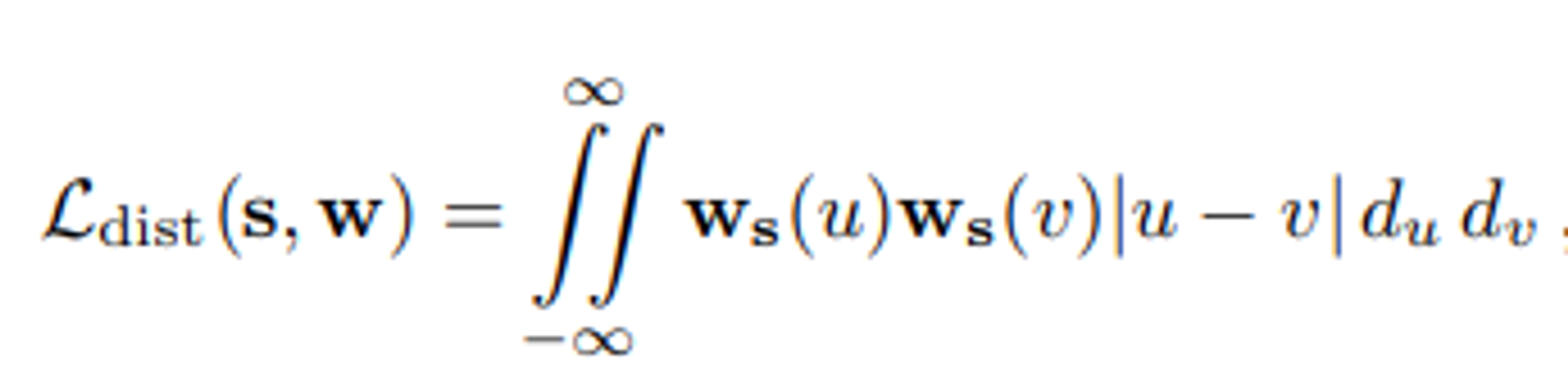
s는 각 구간의 위치를 나타내며, w는 각 구간에 할당된 가중치
|u - v|: u와 v는 구간상의 두점이며, 이 두점 사이의 거리를 나타낸다.
ws(u)와ws(v): u와 v점에서의 가중치

이 Loss 함수는 전체적으로 NeRF 모델이 광선을 따라 특정 구간 내에 있는 밀도(weight)가 가능한 한 집중되도록 유도한다.

위의 이중 적분 표현을 단순화 해서 실제로는 아래의 수식을 사용한다고 나왔다.

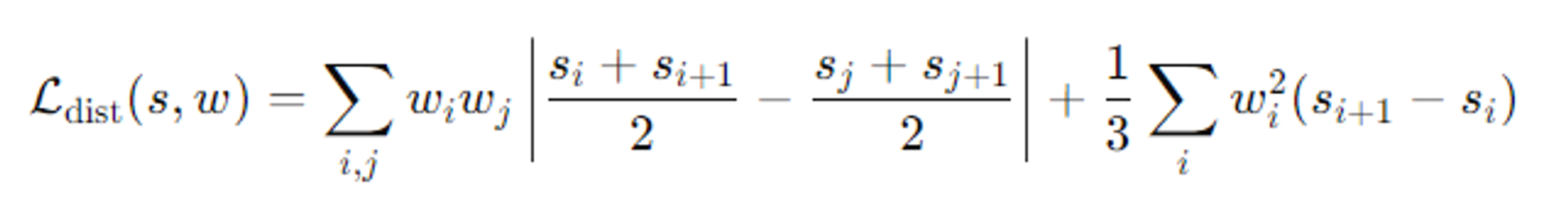
첫번째 항
- 각 구간 i와 j에대한 구간의 중간점들 사이의 거리를 가중치로 곱해 계산
- 이전처럼 구간 사이의 거리가 멀수록 loss값을 증가시킨다. 따라서 구간들이 가능한 한 가까이 있도록 유도한다.
두번째 항
- 각 구간의 길이에 대해 구간의 가중치를 곱해 계산
- 각 구간이 가능한 밀집되도록 유도

즉 두 항은 모두 광선의 구간들이 가능한 한 좁고 밀집되도록 유도한다. 이렇게되면 부자연스러운 작은 밀도 영역이 사라지고, 대신 3D 구조 전체가 잘 정의된 밀도 분포를 가지게 된다. 또한 메라 근처에 부적절하게 높은 밀도를 가지는 영역(즉, 반투명 구름 형태)이 생기지 않도록 한다.

Optimization

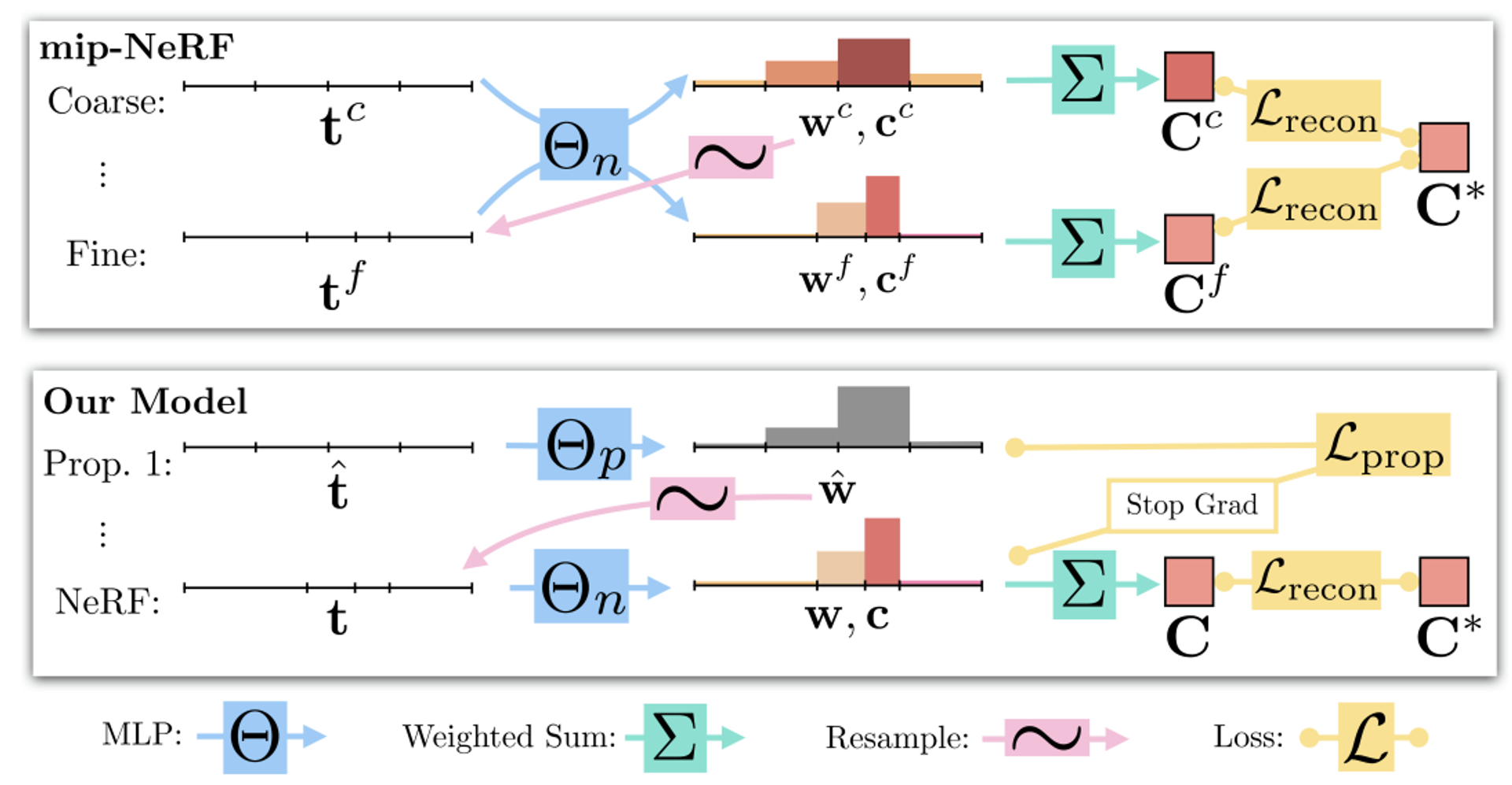
proposal MLP: 256 hidden units(4 layers)

NeRF MLP: 1024 hidden units(8 layers)

proposal MLP는 2번 실행된다. 자세히 보면 Prop 1 이후 …. 부분에 Prop 2가 생략된것이다.

두 번의 샘플링 과정에서 각각 64개의 샘플을 생성하여 $\hat{s}_0$ , $\hat{w}_0$ 와 $\hat{s}_1$ , $\hat{w}_1$ 를 생성한다. 이때 s는 샘플링 값, w는 밀도 값을 나타낸다.

NeRF MLP는 32개의 샘플을 사용하여 최종적으로 s와 w를 계산한다.

Loss

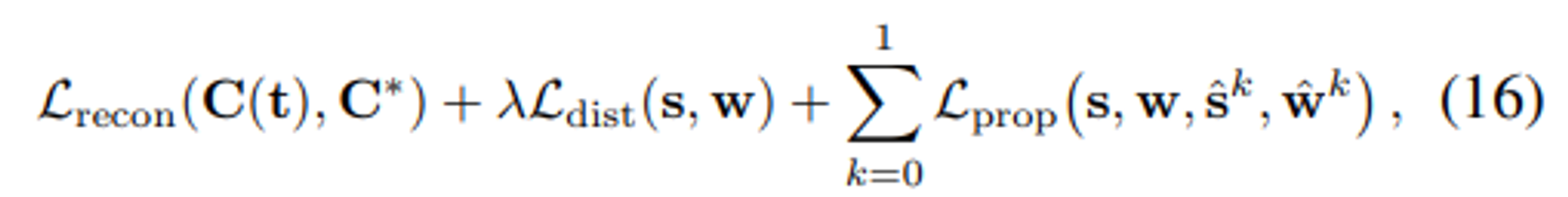
복원 손실 ( $L_{\text{recon}}$ ):

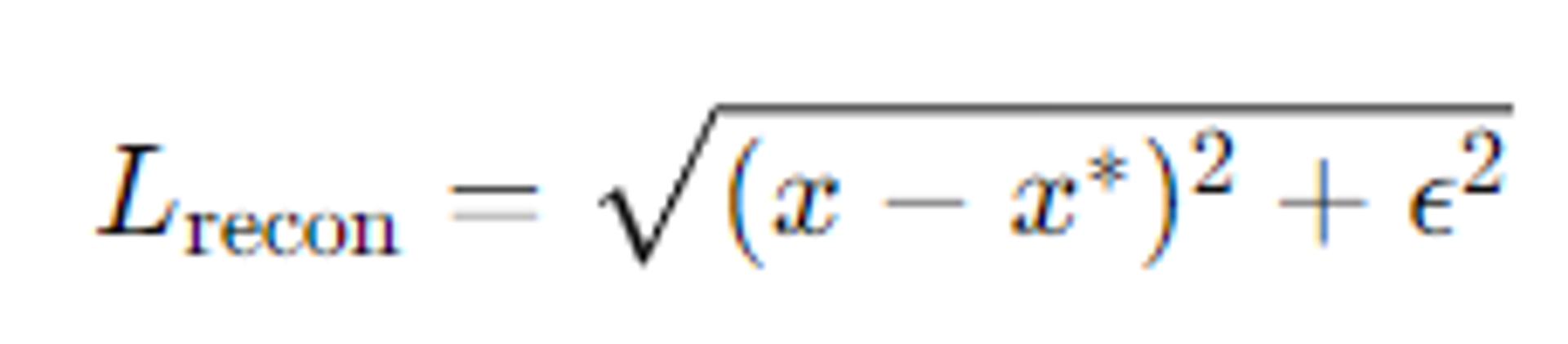
생성된 이미지 C(t)와 목표 이미지 C∗ 사이의 차이를 최소화
MSE와 유사하지만 ϵ가 추가 된 구조(ϵ=0.001)

왜곡 손실 ( $L_{\text{dist}}$ ):

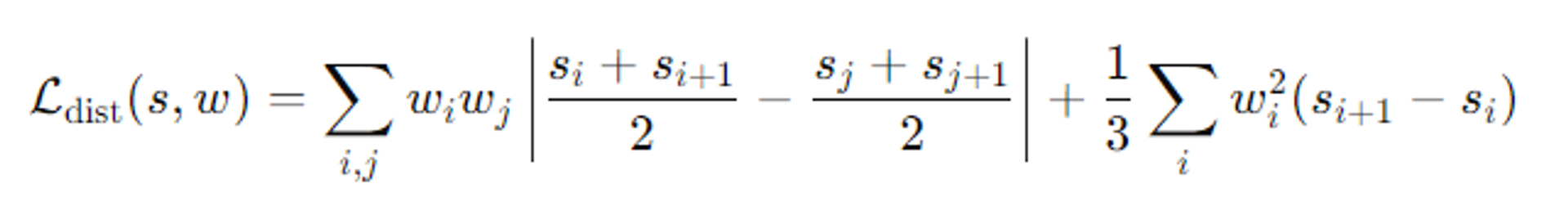
정의: s와 w 값을 기반으로, 3D 공간에서 불필요한 "floaters"나 "background collapse"와 같은 artifact를 줄이는 데 사용된다.
이 손실과 복원 손실 간의 균형을 맞추기 위해 λ=0.01로 설정된다.

제안 손실 ( $L_{\text{prop}}$ ):

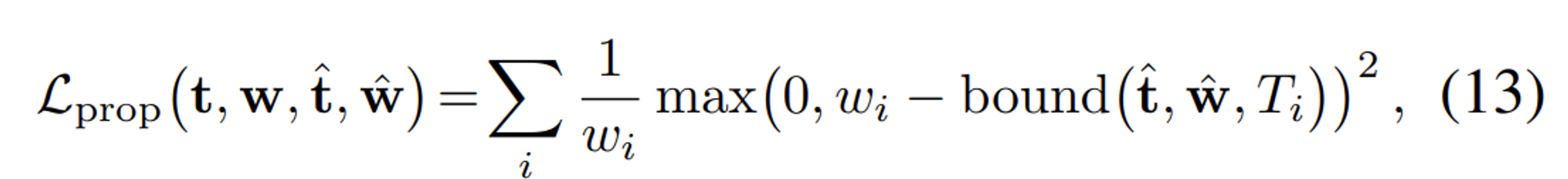
Proposal MLP의 샘플링 과정에서 생성된 $\hat{s}_k$ , $\hat{w}_k$ 와 NeRF MLP의 결과 s,w 사이의 차이를 최소화
stop-gradient 기법을 사용하여 Proposal MLP의 파라미터 업데이트가 NeRF MLP의 파라미터 업데이트와 독립적으로 이루어지도록 한다.

mip-NeRF와의 차이점: 250k iterations of optimization with a batch size of $2^{14}$

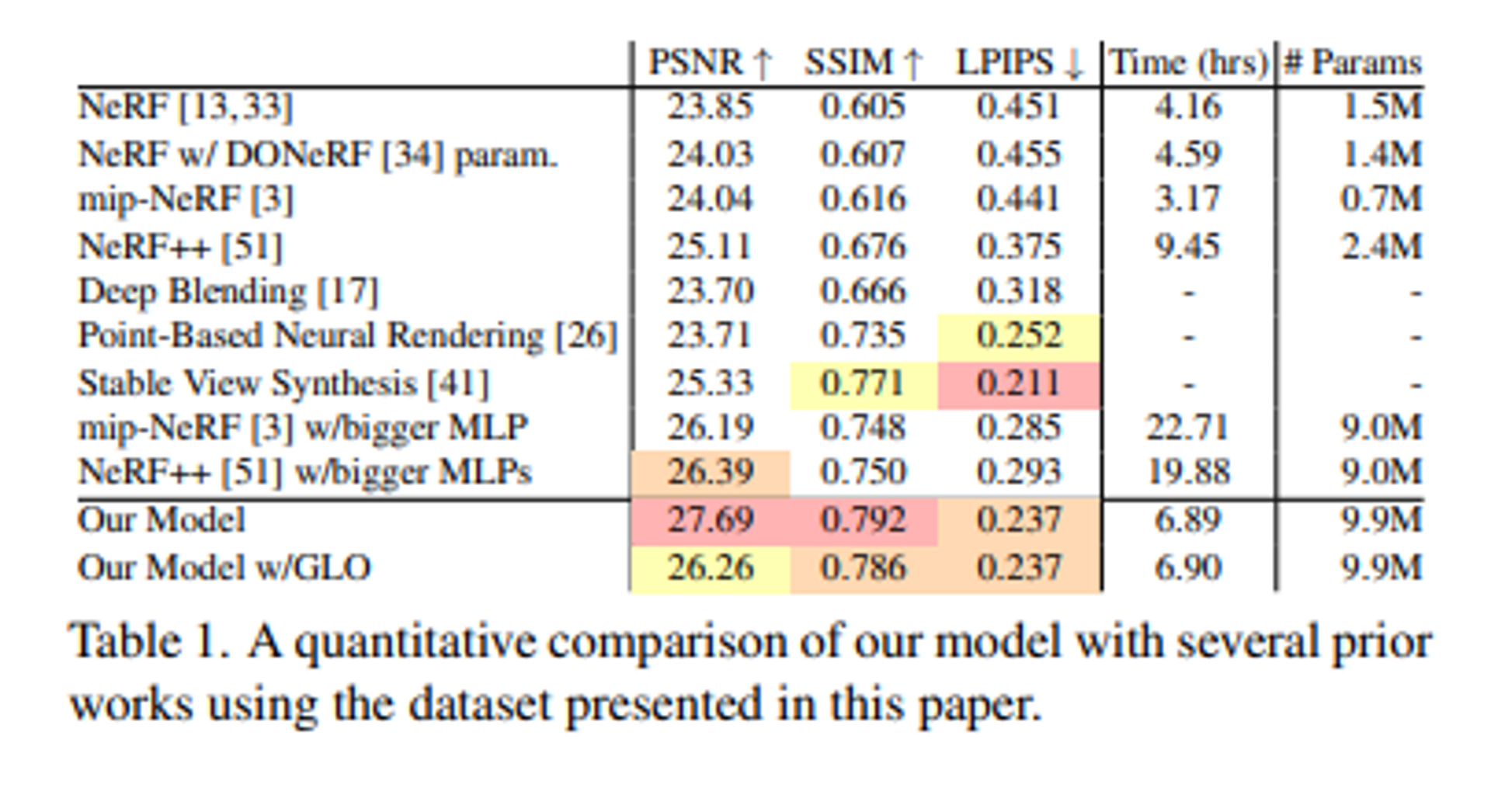
Results

추후에 업데이트 하도록 하겠습니다.

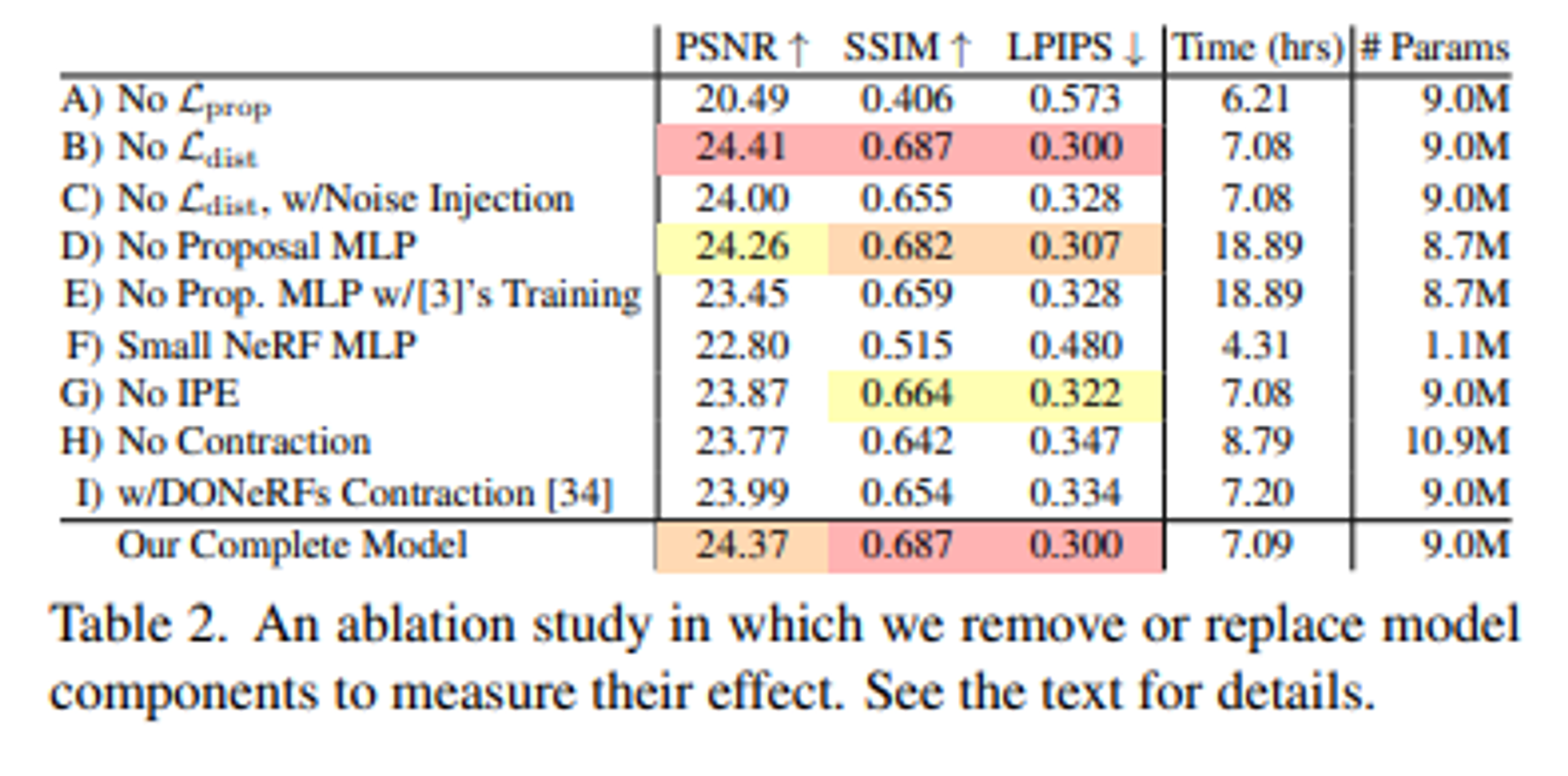
Ablation study

Limitations

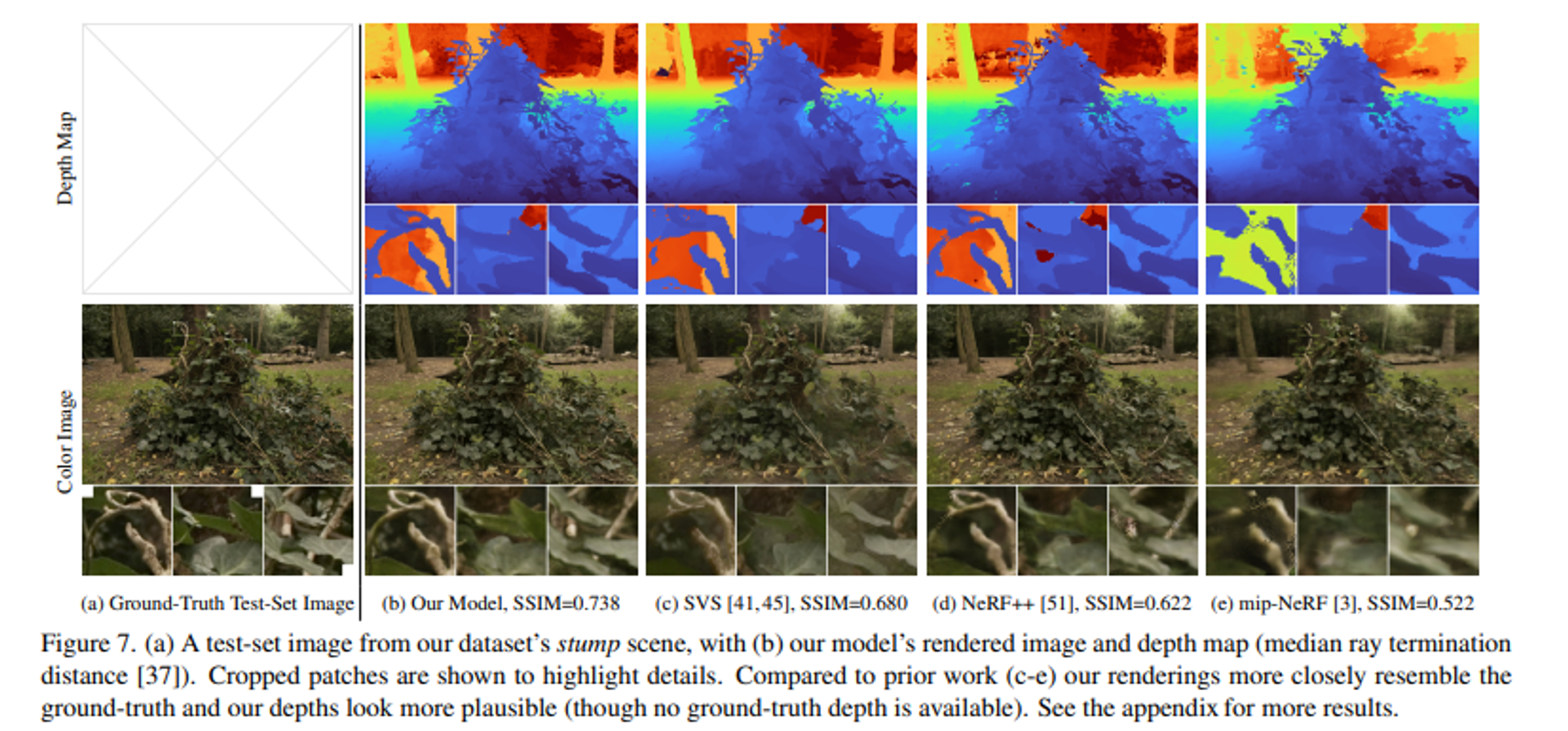
얇은 구조와 세부 사항의 손실
- 예를 들어, 자전거 장면에서 타이어의 스포크(살?)나 나무 그루터기 장면에서 잎맥과 같은 세밀한 디테일이 제대로 재현되지 않을 수 있다. 이는 mip-NeRF 360 모델이 이전 모델들보다 성능이 뛰어나더라도 여전히 특정한 섬세한 부분을 캡처하는 데 어려움이 있다는 것을 의미
카메라 위치에 따른 품질 저하:
- mip-NeRF 360 모델은 특정 시점에서 장면을 재구성하는 데 강점을 가지지만, 카메라가 장면의 중심에서 멀어질 경우에는 뷰 합성의 품질이 떨어질 수 있다. 이는 모델이 장면의 중심 근처에서 더 잘 작동한다는 의미
긴 학습 시간:
- mip-NeRF 360 모델을 사용하여 장면을 재구성하려면 GPU를 사용하여 몇 시간 동안 학습을 해야 한다.

이한결

열정으로 가득할 페이지

이전 포스트

CLIP-Mesh: Generating textured meshes from text using pretrained image-text models 논문 리뷰

다음 포스트