Conditional, Unconditional, Multi-modal point cloud diffusion 모델을 만든 논문입니다. Standfor부터 MIT 까지 뛰어나신 분들이 작성하신 논문이니 어떻게 모델을 계발 했는지 알아보도록 하겠습니다.

Point-Voxel Diffusion

Formulation

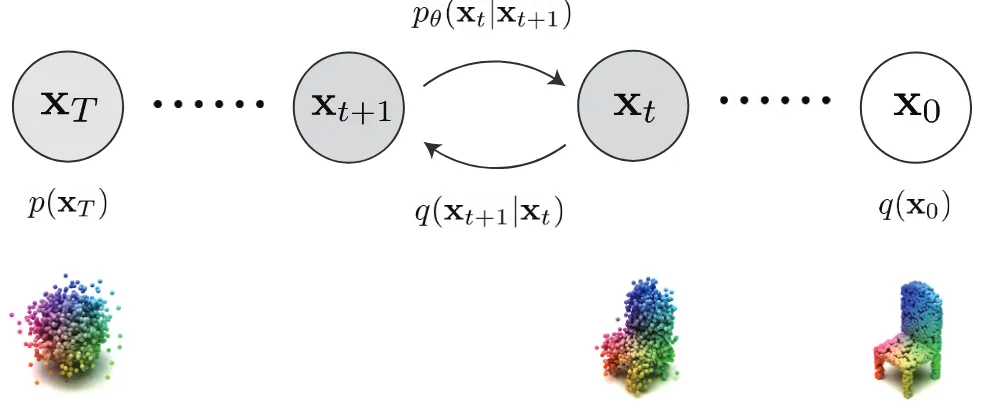
일반적인 Diffusion 모델의 설명입니다.

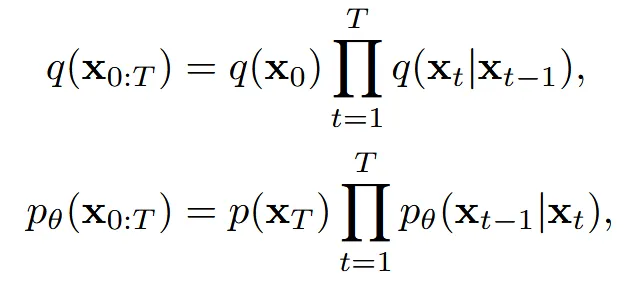
일반적인 diffusion 모델처럼 T시점은 Gaussian noise이고, $x_0$시점은 이미지가 아닌 여기서는 우리가 원하는 형태의 point cloud를 갖습니다. 첫번째 수식은 노이즈를 추가하는 forward process, 두번째 수식은 노이즈를 제거하는 reverse(generative) process입니다.

Training objective

해당 부분도 diffusion의 Variational lower bound에 대한 설명입니다.

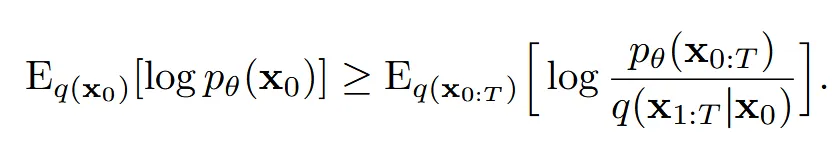
$p_{\theta}(x)$를 구하기 위해서 우리는 variational lower bound를 maximize합니다. 이때 분모의 과정은 forward process로 이미 정해진 만큼의 노이즈를 추가하는 과정입니다. 따라서 분모가 given일 때 분자를 maximize하는 과정이 필요합니다.

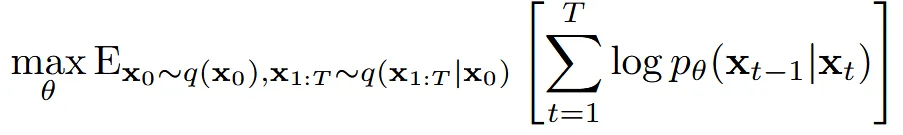
분모를 제거한 maximize variational lower bound 수식은 위와 같습니다.

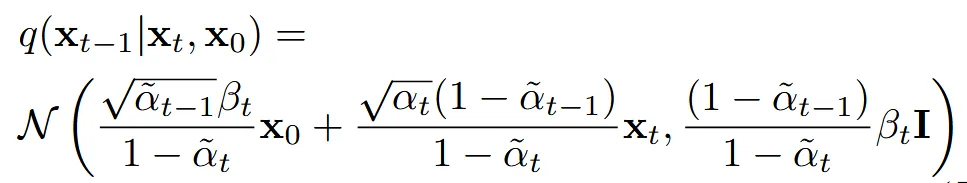
또한 모든 timestep에서의 분포는 Gaussian이기 때문에, 각 시간 단계 𝑡에서의 reverse process 분포 $q(x_{t−1} ∣x_t ,x_0)$는 복잡한 평균과 분산으로 나타낼 수 있으며, 이 평균과 분산은 고정된 노이즈 스케줄 $B_t$에 의해 결정됩니다. 이러한 평균을 직접 예측하는 대신, 우리는 평균을 간접적으로 계산할 수 있는 노이즈(𝜀) 를 예측하는 방식을 사용합니다.

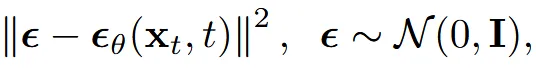
Shape Completion

핵심 아이디어는 이미지로부터 partial shape를 얻고, 해당 부분은 고정하고 나머지 부분만 예측하자는 것입니다.

이미지로부터 얻은 partial shape을 $z_0$이라 하고, 우리가 예측해야 할 나머지 점들을 $\tilde{x_0}$라고 하면 전체 점은 $x_0 = (z_0, \tilde{x_0})$으로 표현할 수 있습니다.

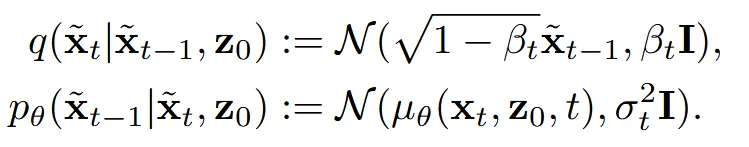
Diffusion 과정을 진행할 때 위의 $z_0$이 고정된 conidtion으로 들어가면서 $\tilde{x_0}$을 예측하도록 설계 됐습니다.

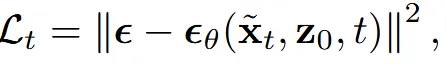
노이즈를 예측하는 과정도 동일하게 L2 loss를 사용하는데 여기서 $z_0$는 loss를 계산하지 않고 오직 $\tilde{x_0}$만 계산하도록 설계 합니다.

Experiments

Shape Generation(Unconditional)

해당 부분의 결과는 입력값이 아무것도 없이 그냥 비행기, 차, 의자로만 학습한 가중치를 이용해서 2048개의 모든 point를 예측했을 때의 결과입니다. 즉 윗부분에서 $z_0$이라는 condition 부분이 존재하지 않는 경우입니다.

Shape Completion(Conditional)

이번에는 맨왼쪽처럼 depth를 통해서 partial shape을 얻어서 이걸 $z_0$으로 사용했을 때의 결과입니다.

Multi-Modal Compleition

Diffusion 모델을 사용했기 때문에 같은 Partial shape을 주더라도 서로 다른 결과가 나올 수 있습니다. 참고로 여기서 말하는 multi-modal은 여러개의 modality를 입력으로 사용했다는 것이 아닌 1개의 입력으로 다양한 결과를 나타낼 수 있다는 의미로 사용했습니다.

왼쪽 예시는 partial view가 많이 보이는 경우 비슷한 결과들이 나오지만, 오른쪽 같이 partial view가 제한적일 경우 결과들이 다양하게 나옵니다.