Point Cloud에 Diffusion 모델을 도입한 거의 시초 논문입니다. 이후의 논문들은 많이 읽어봤는데 초기에는 어떻게 처음 아이디어를 제시했는지 확인해보도록 하겠습니다.

Diffusion Probabilistic Models for Point Clouds

Fromulation

Point Cloud: N개의 점들의 집합, $X^{(0)} = \{x_i^{(0)}\}^N_{i=1}$ → 각각의 점들은 독립되게 움직일 수 있습니다.

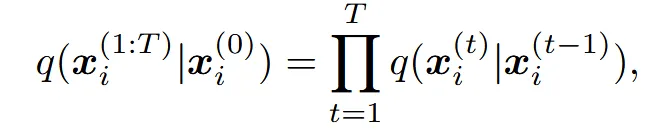
하나의 점에 대해서 Diffusion의 forward process는 다음과 같습니다.

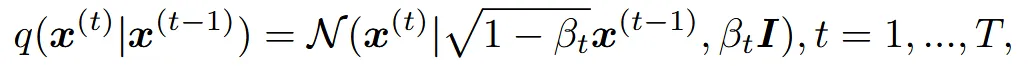
잘 아시는 diffusion 수식입니다. $B_t$는 variance schedule입니다.

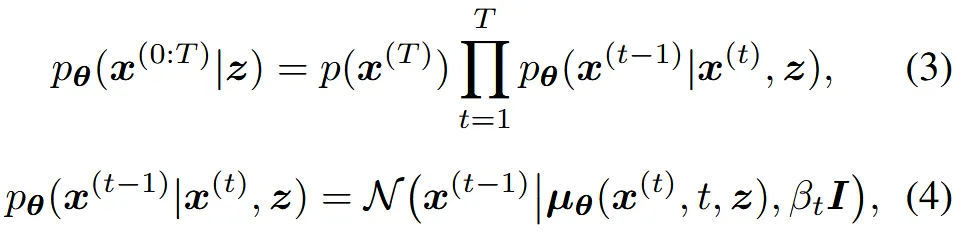
Diffusion에서 time step 0에서가 우리가 원하는 형태의 데이터이기 때문에 위의 reverse process를 통해서 T=0인 시점을 예측해야 됩니다. z는 shape latent로 우리가 생성하고자 하는 모양에 대한 정보를 담고 있는 잠재 변수입니다.

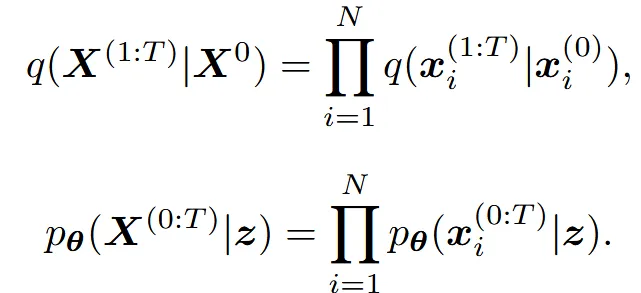
이를 N개의 Point cloud로 확장하면 위와 같이 N개의 독립적인 각 점들이 학습 될 것입니다.

Training Objective

사실 해당 부분은 그냥 diffusion 수식 설명이라서 넘어가도 괜찮습니다.

목표는 reverse diffusion process의 log-likelihood를 maximize 하는 것입니다. 하지만 log-likehood를 maximize하는 것은 계산이 어렵기 때문에 variational lower bound를 maximize합니다.

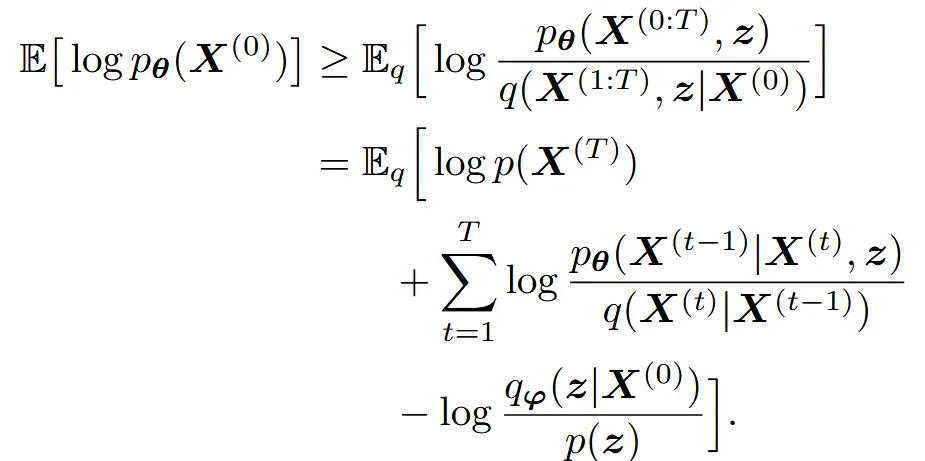
위의 식을 maximize하는 Loss는 아래와 같습니다.

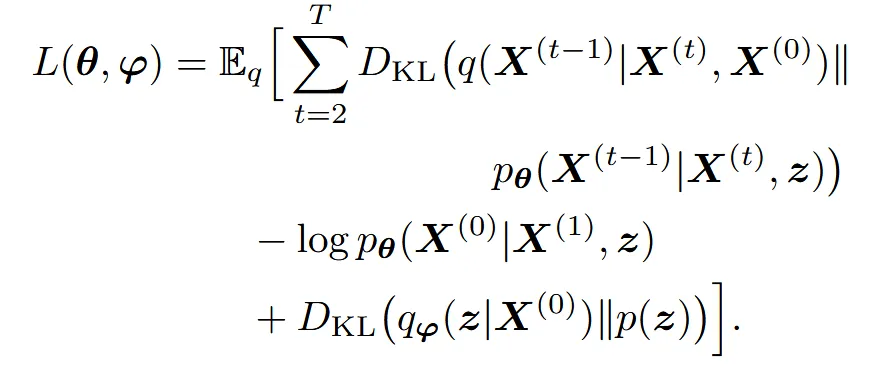
각 점들이 독립적이기 때문에 위의 loss를 하나의 점에 대해서 나타내면 결론적으로 아래와 같이 나타납니다.

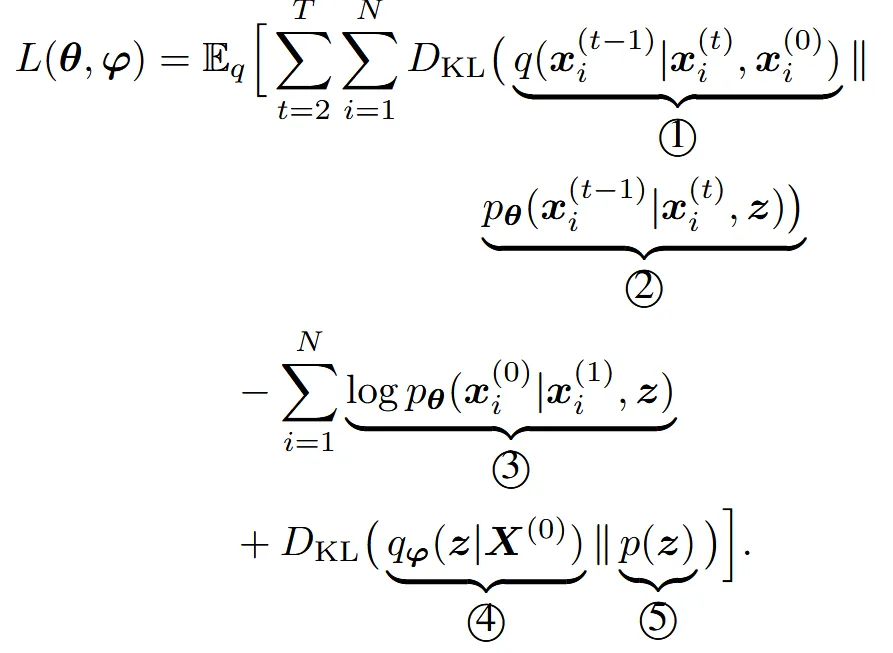
1번수식

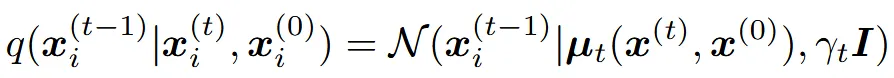
정확한 Gaussian 공식으로 계산할 수 있습니다.

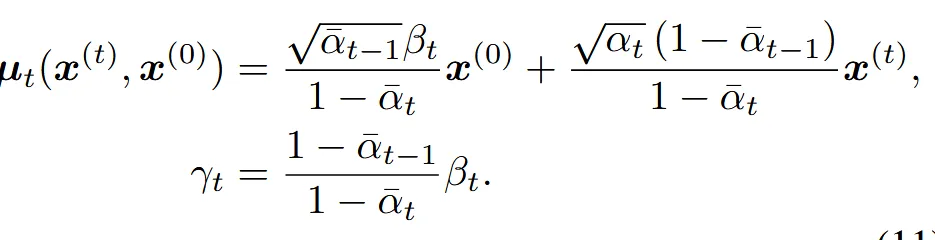
2번 수식

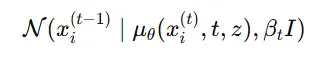
우리가 학습해야 되는 값입니다.

3번 수식

t=1 일 때 즉 최종 output을 얼마나 잘 복원하는지를 봅니다.

4번수식

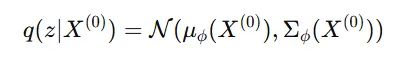
VAE에서 쓰는 구조 그대로 point cloud를 z라는 latent로 압축한 분포입니다.

5번 수식

latent z의 prior 분포로서 Gaussian noise(N(0,1))을 사용합니다.

Training Algorithm

이부분도 DDPM과 동일한 수식입니다.

Model Implementations

Point Cloud Generator

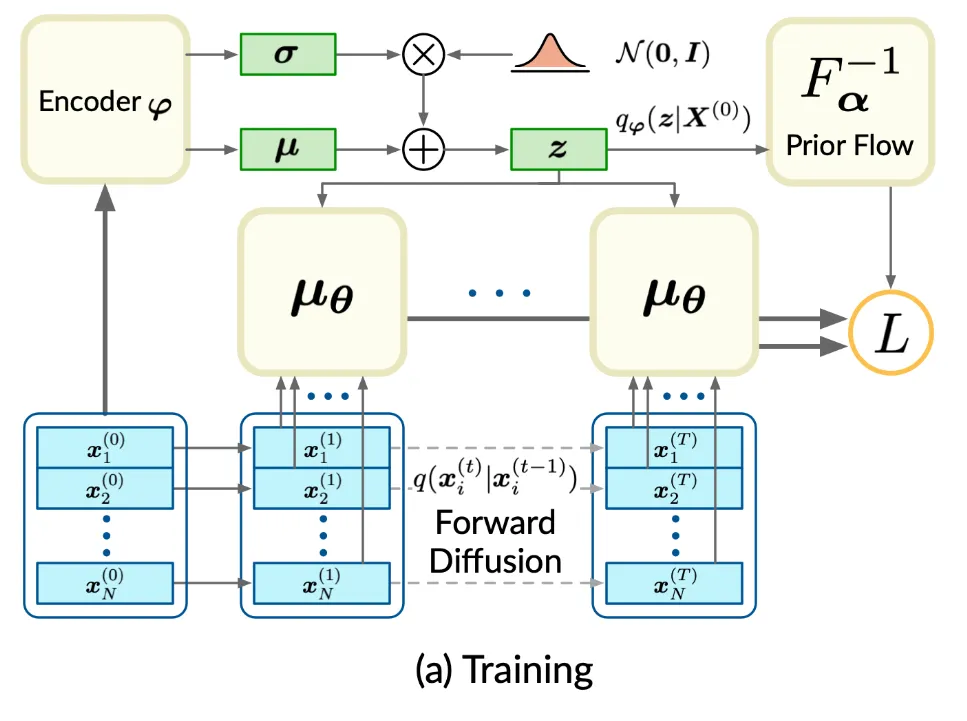
Point Cloud가 복잡한 구조를 갖고 있기 때문에 더 유연한 prior 분포가 필요합니다. 따라서 normalizing flow를 적용해서 gaussian noise w를 복잡한 분포로 변환합니다.

변환하는데 사용되는 개념이 affine coupling layers인데 해당 개념은 위의 개념에서 맨왼쪽의 우리가 target으로 하는 point cloud를 Encoder를 통해서 임베딩 값을 얻고, 임베딩의 절반은 그대로 두고, 절반은 위에처럼 변형을 가하는 과정입니다. 이는 역변환도 변환을 적용한 부분만 다시 원상 복귀 하면 되기 때문에 쉽게 구할 수 있습니다.

정리하면 gaussian noise w를 복잡한 분포로 보내야하는데 그걸 affine coupline layers를 이용해서 보낼거고, 보내는 목표는 target point cloud의 Encoder를 통해서 나온 임베딩 값과 유사하게 하는 것입니다.

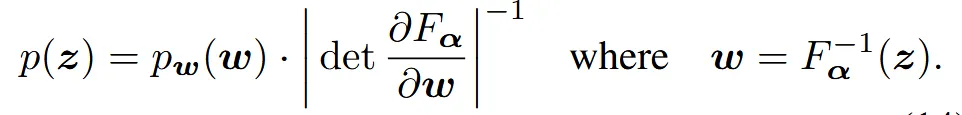
이를 수식적으로 나타내면 위와 같습니다.

Point Cloud Encoder로는 PointNet을 사용했습니다.

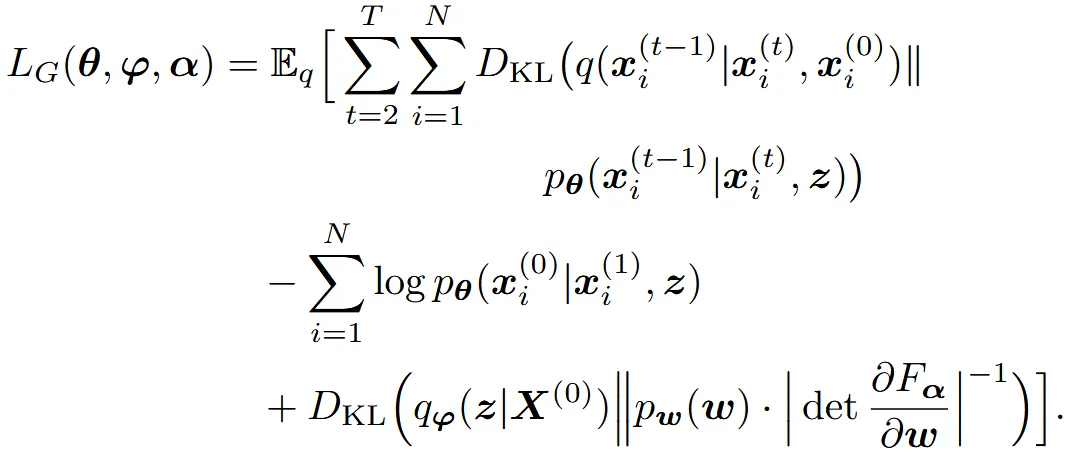
위의 내용을 반영한 최종적인 loss는 아래 KL Divergence 항이 추가된 loss가 됩니다.

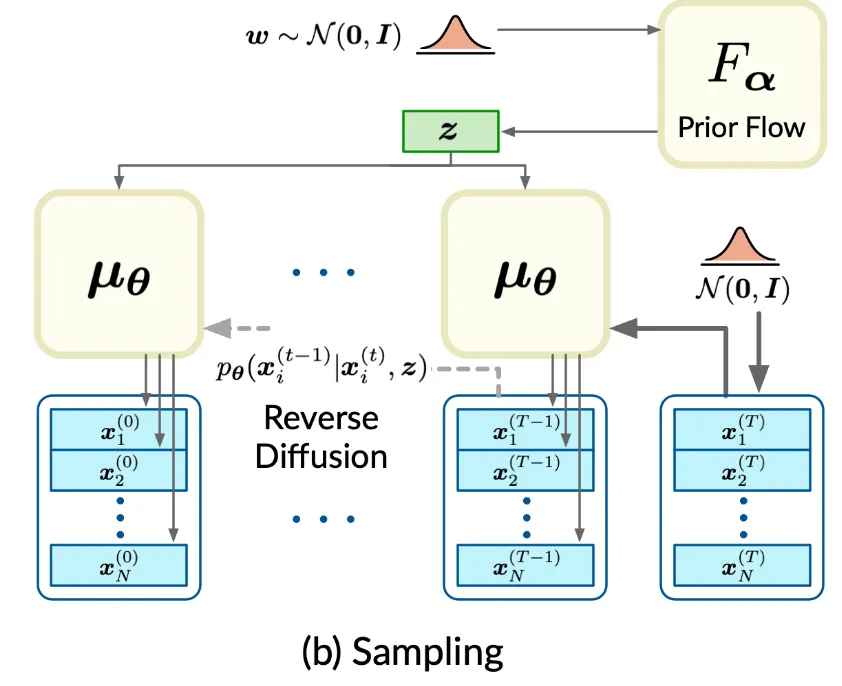
Sampling 할 때는 위의 사진과 같이 Gaussian noise를 prior flow에 통과된 값을 이용해서 denoising을 진행합니다.

Point Cloud Auto-Encoder

지금까지 설명한 구조를 다시 정리하는 부분입니다.

No Condition?

지금까지 설명으로는 image나 text처럼 condition으로 들어가는 값에 대한 설명이 없는데, 생각해보니 latent z자체가 그냥 condition 처럼 되는것 같습니다. 즉 우리가 비행기를 생성하고 싶으면 비행기로만 학습한 latent z를 만들고, 이를 이용해서 diffusion을 통과하면 해당 비행기 point cloud가 생성되게 됩니다.

Experiments