출처[LECTURE05, LECTURE06]
강의 영상: https://mhsung.github.io/kaist-cs492d-fall-2024/
해당 강의를 기반으로 추가적인 코드 구현과 설명을 정리했습니다.
DDPM 논문리뷰: https://velog.io/@guts4/Basic-Generative-Model-DDPM
DDPM 논문수식: https://velog.io/@guts4/DDPM-%EC%88%98%EC%8B%9D-%EB%B0%8F-%EB%85%BC%EB%AC%B8-%EC%99%84%EB%B2%BD-%EB%B6%84%EC%84%9D
GAN 논문리뷰: https://velog.io/@guts4/GANGenerative-Adversal-Network-%EB%85%BC%EB%AC%B8%EB%A6%AC%EB%B7%B0
DDIM 논문리뷰: https://velog.io/@guts4/Denoising-Diffusion-Implicit-ModelsDDIM-%EB%85%BC%EB%AC%B8-%EB%A6%AC%EB%B7%B0
Classifier Guidance 논문리뷰: https://velog.io/@guts4/Diffusion-Models-Beat-GANs-on-Image-Synthesis-%EB%85%BC%EB%AC%B8-%EB%A6%AC%EB%B7%B0
Denoising Diffusion Implicit Models(DDIM)
Direct Sampling vs Generative Models
Direct Sampling: 기존의 데이터셋에서 데이터를 직접 선택하여 제공하는 방식
- 데이터를 직접 저장하고 사용해야 하기 때문에 많은 저장공간이 필요
- 이미 저장된 데이터 중 선택하는 방식이기 때문에 새로운 데이터를 생성하기 어렵습니다.
Generative Model: 데이터를 분포를 학습하여 데이터를 생성
- Efficiency and Scalability
- 데이터를 저장하지 않아도 되기 때문에 저장공간 절약
- Novelty and Diversity / Privacy and Security Concerns
- 기존 데이터가 아닌, 새로운 샘플을 생성할 수 있습니다.
- 이전 데이터를 사용하는 것이 아니기 때문에, 개인정보 보호 및 보안 측면에서 유리
- Adaptability to New Conditions
- 주어진 조건에 맞춰 새로운 데이터를 생성하기에 용이
Connection to Score-Based Models
Score Function
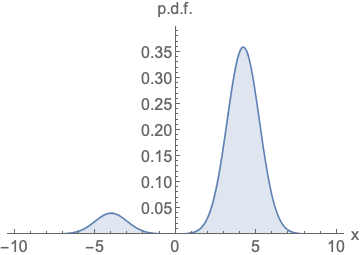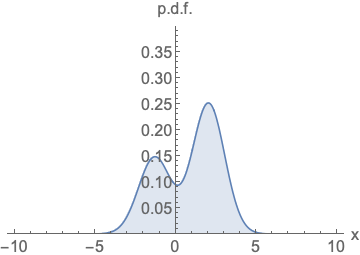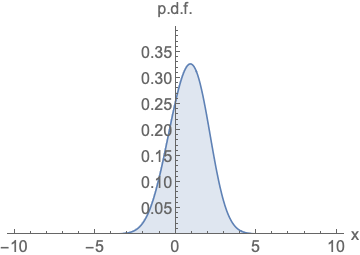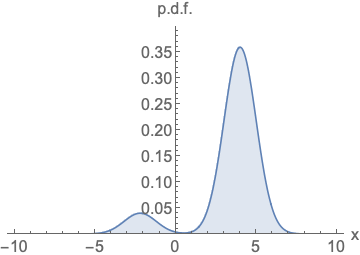
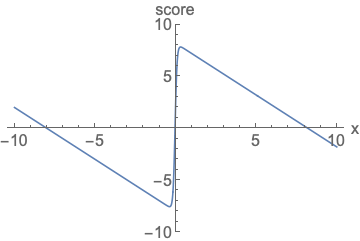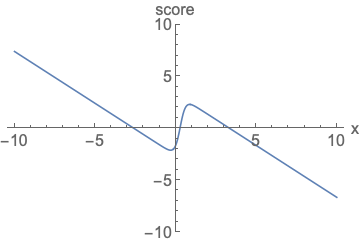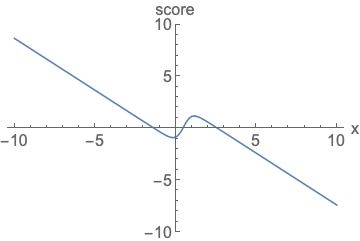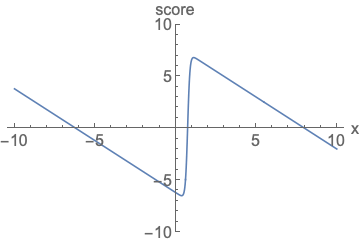
주어진 확률 밀도 함수(p.d.f)의 로그를 x에 대해 미분한 값 → 특정 데이터 포인트에서의 확률 분포의 변화량
즉 해당 함수는 데이터가 왼쪽과 같은 분포를 따를 때, 이 분포 내에서 특정 위치에 있는 데이터의 변화 경향을 파악하는 역할.
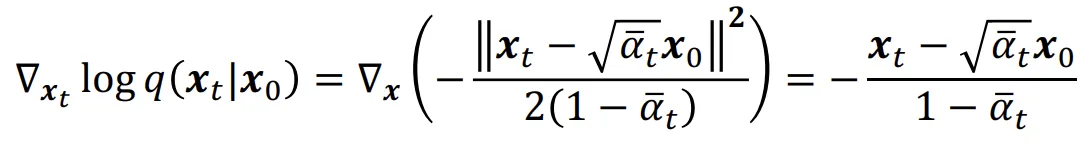
우리가 이전 강의에서 배운 DDPM의 수식 의 분포에 대해서 log의 미분을 취한 값, 즉 score function을 구하면 위와 같습니다.
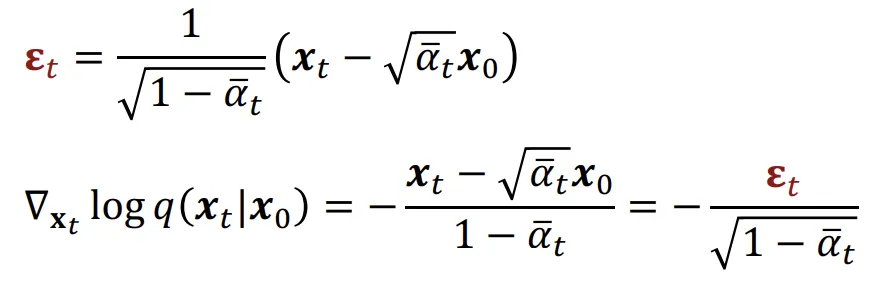
이전 강의에서 노이즈(epsilon) 값에 대해서도 수식으로 나타냈는데, 이를 위에서 구한 값에 대입하면 score function을 노이즈에 대해서 나타낼 수 있습니다.
이를 통해 noise predictor는 score function에 어떠한 상수배를 취한 값을 예측하는 과정과 동일한 과정이라고 수식을 통해서 확인할 수 있습니다.
Tweedie’s Formula
정규 분포에서 데이터 x를 샘플링 할 때 해당 데이터의 True Mean 값을 추정하는 방법입니다.
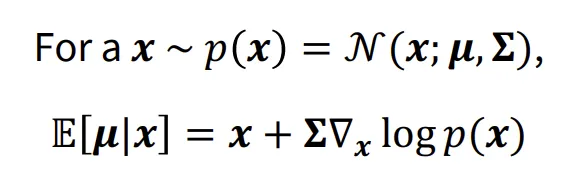
수식에서 보이는 것처럼 단순히 x값만을 평균으로 갖는 것이 아니라, 분산과 score function을 곱한 값으로 나타내어 확률 밀도가 높은 방향의 보정적인 값을 더합니다.
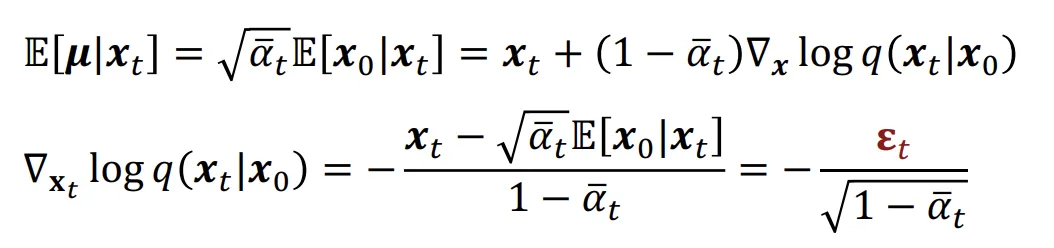
해당 수식을 기반으로 수식을 전개하면 이전 score function에서 보았던것과 같은 동일한 식을 얻을 수 있습니다.
Langevin dynamics
LECUTRE02: https://velog.io/@guts4/Basic-Generative-Model-Statistical-Perspective
해당 강의에서 어떤 데이터의 분포(PDF)를 알고 있을 때 우리는 직접적으로 샘플링 할 수 있다는 것을 확인 했습니다.
만약에 우리가 score function을 알고 있다면, 어떠한 데이터 분포를 알지 못하더라도 socre functio을 Langenvin dynamics를 이용해서 데이터의 분포를 알아낼 수 있습니다. 이것이 score function이 중요한 이유입니다.
그러면 score function을 데이터의 분포로 바꿔주는 Langevin Dynamics는 멀까요?
Langevin Dynamics는 초기 샘플을 점진적으로 업데이트하여 목표 확률 분포에 도달하게 만드는 iterative(반복적) 프로세스입니다.
- 초기 확률 분포(prior distribution)에서 x를 샘플링 (랜덤 노이즈)
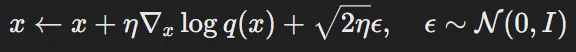
- 이후에 위의 수식과 같이 업데이트를 반복합니다.
- η: learning rate(step size)
수렴(Convergence) 조건
- η → 0: step size를 점점 줄여야합니다.
- T → ∞: 충분히 많은 반복이 필요합니다.

데이터를 보면 초기에 넓은 분포로 흩어져 있었지만, score function(화살표)를 통해서 점점 한 곳으로 뭉치는 것을 확인할 수 있습니다.
Score-Based Models
위에서 노이즈를 예측하는 과정이 score function을 예측하는 과정과 동일하게 작동하는 것을 확인했었습니다. 그러면 노이즈 예측이 아닌 score function을 예측하는 학습과정이 어떻게 진행되는지 설명해드리도록 하겠습니다.
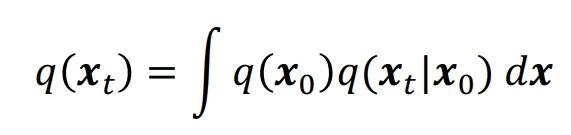
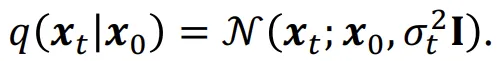
q(x)를 Gaussian들의 혼합된 형태라고 가정해보겠습니다. 그러면 위와 같은 수식으로 나타낼 수 있습니다.
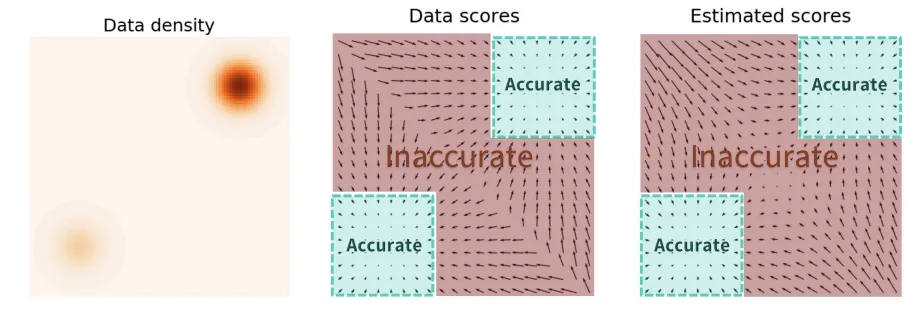
가 작다면 데이터들은 평균 근처에 존재할 것이고, 반대로 크다면 평균으로부터 멀리 떨어져 있을 것입니다. 작은 경우에 조금더 집중하자면, 데이터들이 high density영역에 대해서는 정확한 결과를 얻을 수 있지만, low density 영역에 대해서는 좋지 않은 결과를 낼 것입니다.

반대로 분산이 큰 경우 Inaccurate 영역 즉 low density에 대해서는 어느정도 성능을 낼 수 있지만, 반대로 이전에 정확했던 high density 영역의 정확도는 떨어지게 될것이빈다.
Annealed Langevin Dynamics
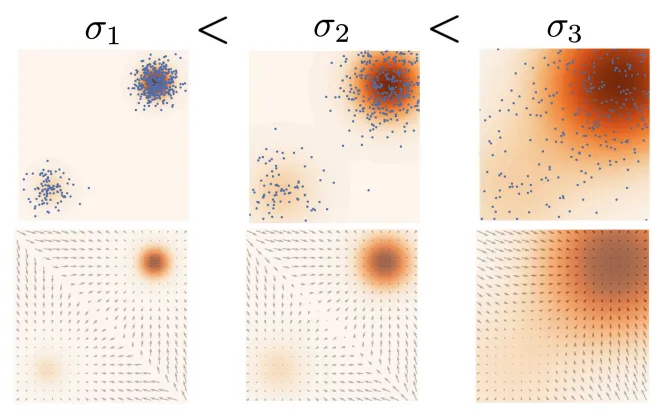
이러한 장단점들을 해결하기 위해 초기에는 큰 분산을 통해서 low density를 학습하고, 이후에 분산값을 줄여가면서 high density의 정확한 결과를 얻는 학습 방식이 Annealed langenvin dynamics입니다.
Denoising Diffusion Implicit Models(DDIM)
GAN: High quality + Fast Sampling // Mode Collapse
VAE: Fast Sampling + Mode Converage // Low quality
DDPM: High quality + Mode Convergae // Slow Sampling
어떻게하면 DDPM의 단점인 속도를 빠르게 할 수 있을까? 라는 의문을 해결하는 논문이 DDIM입니다.
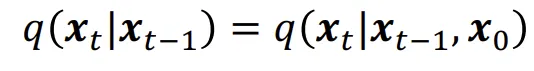
DDPM은 위의 수식과 같이 이전단계에만 영향을 받는 Markovian 과정입니다.
Forward process
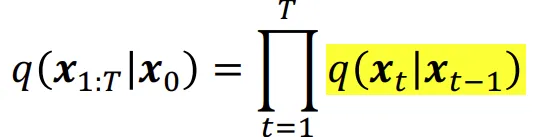
위의 수식은 원래 DDPM에서 사용하는 Forward process 수식입니다. t시점은 t-1시점에만 영향을 받는다는 수식입니다.
<유도과정>

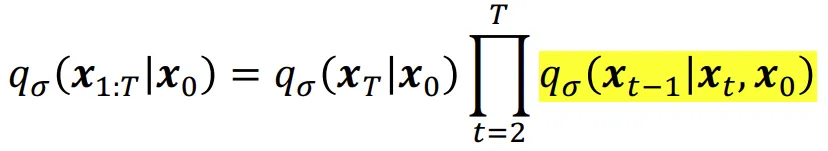
위의 수식은 마르코프 체인을 사용하지 않는 DDIM 수식입니다. 첫번째로 입력 데이터()로 부터 의 데이터 분포를 샘플링하고, 시점의 샘플은 와 을 이용해서 얻습니다. 그리고 노란색 형광펜 쳐져있는 부분의 각 step은 이전 시점과 입력 데이터의 영향을 받는다는 점입니다.
그러면 도 결국 어떠한 분포일 것인데 이 분포는 어떻게 구할 수 있을까요?
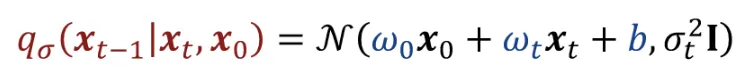
는 와 로 이루어져있고, 이에 대해서 위와 같이 나타낼 수 있습니다. 그러면 3가지 매개변수 , , b를 찾아보도록 하겠습니다.
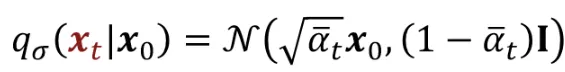
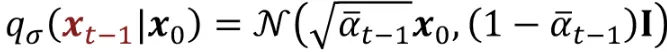
와 는 위와 같이 DDPM에 구한 방법으로 나타낼 수 있습니다.
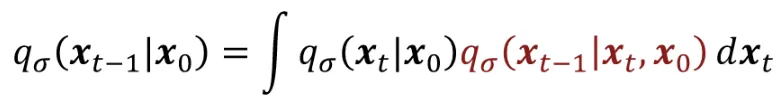
마르코프 체인에 따라서 위와같이 식을 표현할 수 있습니다. 상태를 구하기 위해서 에서 로의 분포를 구한 후 다시 로 가는 과정입니다.
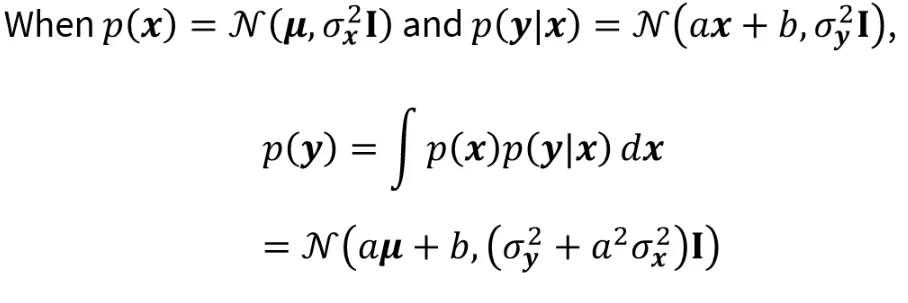
위의 식은 이전 마르코프 체인을 풀기위한 Solution(공식)이라고 보시면됩니다. 결론적으로 우리는 2가지 부분을 알고 있고 (, ), 나머지 하나(를 구하려고 하고 있기 때문에 위의 식을 통해서 쉽게 구할 수 있을 것입니다.
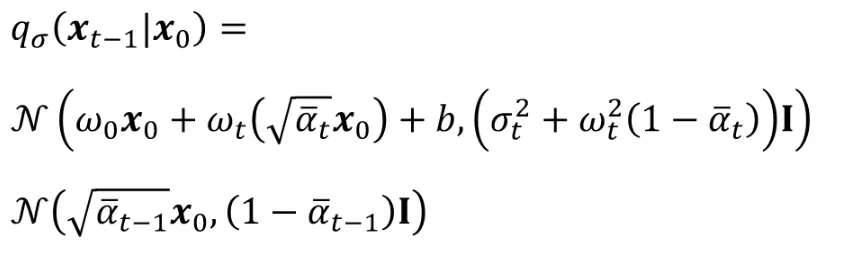
solution에 2가지 값을 대입하면 위와 같은 수식이 나올것이고
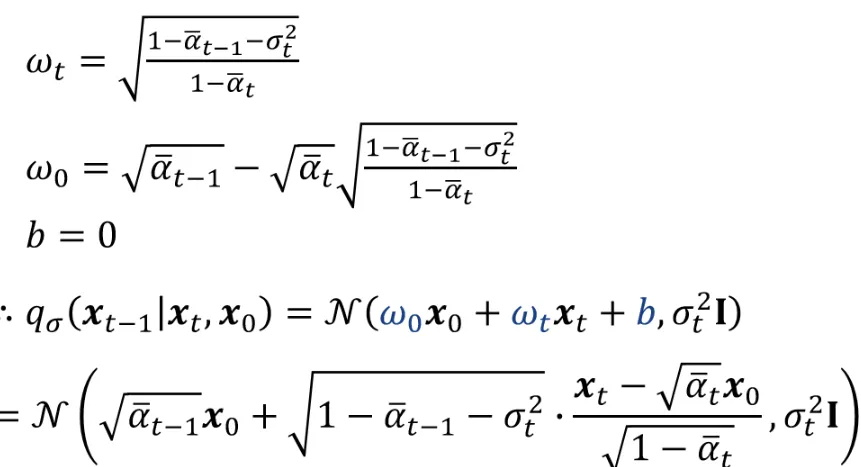
결론적으로 3개의 파라미터를 구하고, 해당 값을 대입하면 맨 아래의 분포를 갖게 됩니다.
Deterministic
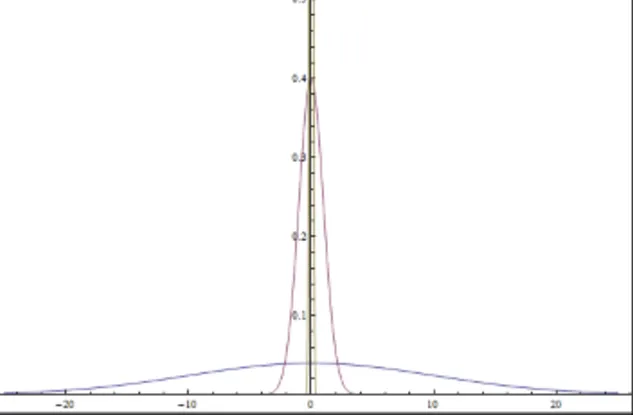
위에서 구한 데이터의 분포에서 분산값이 0이된다면, 데이터들은 모두 평균에 위치하고 결론적으로 경로가 정해진 상태, 즉 deterministic한 상태가 될것입니다.
정리
DDPM
이라는 마르코프 체인이 주어지고, 이를 기반으로 과 이 주어진 것입니다.
DDIM
non-Markovian을 사용하기 위해서 을 먼저 정의하고, 이를 기반으로 과 를 정의합니다.


교수님께서 잘 정리해주신 자료입니다. 차이점을 한눈에 확인할 수 있을 것입니다.
- 평균이 다른 형태로 존재합니다.
- 분산이 DDPM은 고정된 값으로 forward process에서 동작, DDIM에서는 선택 가능한 값으로 동작
DDIM을 요약하면
- DDPM은 DDIM의 특별한 경우이다.
- 평균을 나타내는 수식이 복잡해졌을 뿐, 두 모델의 차이는 없다.(Sampling 차이)
- 따라서 DDIM은 학습을 다시 할 필요가 없다.
- Variance=0인 경우 deterministic하다.
- 적은 수의 step으로도 좋은 결과를 얻을 수 있다.
Classifier-Free Guidance(CFG)
DDPM과 DDIM을 통해서 Diffusion 모델이 이미지를 어떻게 생성하는지 알아봤습니다.
그러면 우리가 원하는 class, 예를 들어서 강아지를 생성하고 싶을 때는 어떻게 해야할까요? 이러한 궁금증을 해결해주는 모델이 바로 Classifier-Free Guidance입니다.

핵심 아이디어는 노이즈를 예측할 때 class label(y)를 condition으로 주어서 노이즈를 예측하게 하는 것입니다.
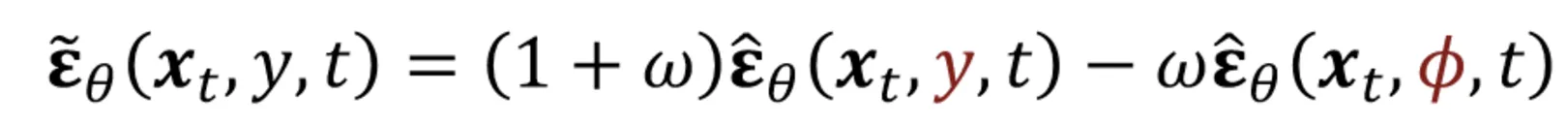
위의 수식과 같이 2가지 부분의 노이즈 예측 term이 존재합니다. 왼쪽은 conditional 노이즈 예측값이고, 오른쪽은 unconditional 노이즈 예측값입니다. w값이 커질수록 condition의 영향이 강해집니다.

w값이 커질수록 더 허스키스러운 이미지가 생성되는 것을 확인할 수 있습니다.
Classifier-Free Guidance의 장점은 적용하기 쉽다는 점과, text뿐만아니라 어떠한 정보도 condition으로 들어갈 수 있다는 점입니다.
단점은 conditional인경우와 unconditional인 경우를 2번 평가해야해서 시간이 더 걸린다는 점입니다.
