[Basic Generative Model] Probability Flow ODE / DPM-Solver

출처[LECTURE14]
강의 영상 및 자료:https://mhsung.github.io/kaist-cs492d-fall-2024/
해당 강의를 기반으로 추가적인 설명을 정리했습니다.

DPM-Solver 논문 리뷰: https://velog.io/@guts4/DPM-Solver-A-Fast-ODE-Solver-for-Diffusion-Probabilistic-Model-Sampling-in-Around-10-Steps-%EB%85%BC%EB%AC%B8-%EB%A6%AC

Generation Speed

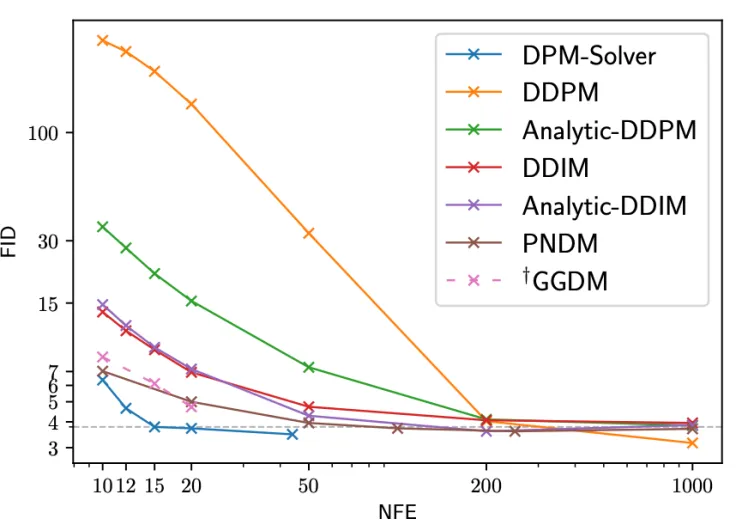
DDPM은 200~1000번의 denoising steps들을 거친 후, DDIM은 50~200번의 denoising steps들을 거친 후 Sampling 결과를 일반적으로 얻을 수 있습니다. 어떻게 하면 더 빠르게 계산하고, 더 좋은 결과를 얻을 수 있을까요? 이 부분에 대해서 설명을 진행하는 강의가 될 것입니다.

SDE → Diffusion Model

SDE와 Diffusion 모델 모두 Forward와 Reverse process를 이용해서 단순한 데이터의 분포로부터 복잡한 데이터를 얻는 과정입니다. 따라서 SDE의 수식을 Diffusion모델에 적용해서 사용할 수 있습니다.

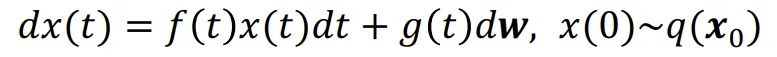
그렇다면 위의 SDE 수식을 어떻게 Diffusion 모델에 적용할 수 있을까요? 위의 식에서 f(t)와 g(t)를 Diffusion 모델의 수식에 적용해야 될 것입니다.

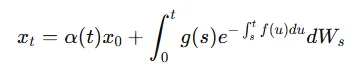
SDE를 해석적으로 푼 해는 위와 같습니다. 시간에 따른 신회 감쇠 비율을 나타내는 a(t)는 f(t)의 누적곱으로 나타낼 것이고, 노이즈의 경우에도 시간에 따라 노이즈가 축적된 값을 나타낼 것입니다. g(s)는 노이즈의 강도, 적분값은 시간적 감쇠율일 것입니다.

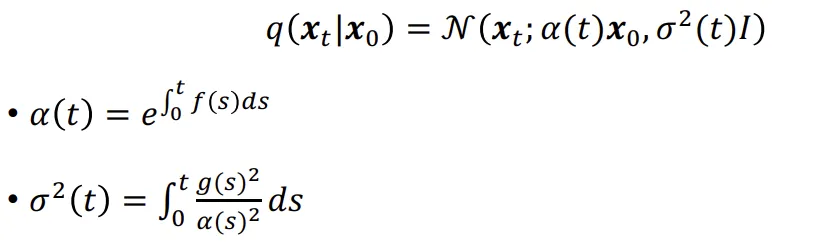
결론적으로 위의 수식과 같은 scale값과 분포 값으로 정의할 수 있을 것입니다.

Diffusion Model → SDE

그러면 반대의 경우도 가능하겠죠? Diffusion model을 SDE에 적용하는 방식을 알아보도록 하겠습니다.

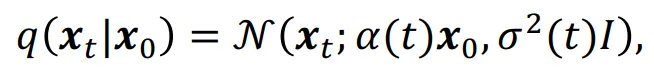
위의 Diffusion 수식을 dx(t) = f(t)x(t)dt + g(t)dw인 SDE의 수식에 적용해야 됩니다. f(t)와 g(t)의 수식은 이전 맨 마지막 부분에 a(t)와 $\sigma$(t)에 대해서 나타낸 수식이 있기 때문에 이를 이용하면 아래와 같이 쉽게 구할 수 있을 것 입니다.

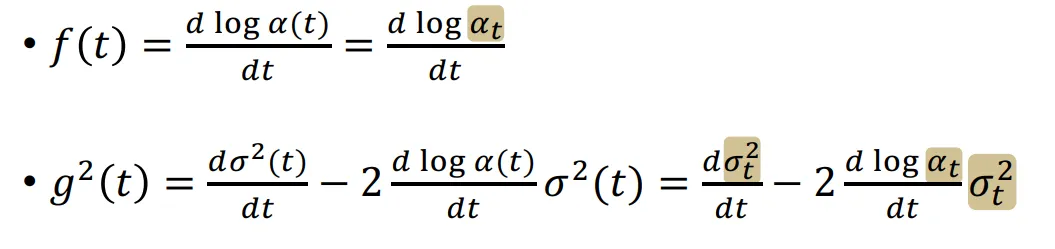
위의 2번째 $g^2(t)$의 수식의 맨 마지막 부분을 어떠한 유도과정을 통해서 진행할 것인데, 사실 해당 과정은 DPM-Solver라는 논문에서 수식을 전개하기 더 쉽게 하기 위해서 변수를 만드는 과정입니다. 그래서 그냥 변수를 어떻게 쉽게 나타내고 싶은데 그 변수를 찾기 위한 유도과정이구나~ 하고 간단하게 보시면 됩니다.

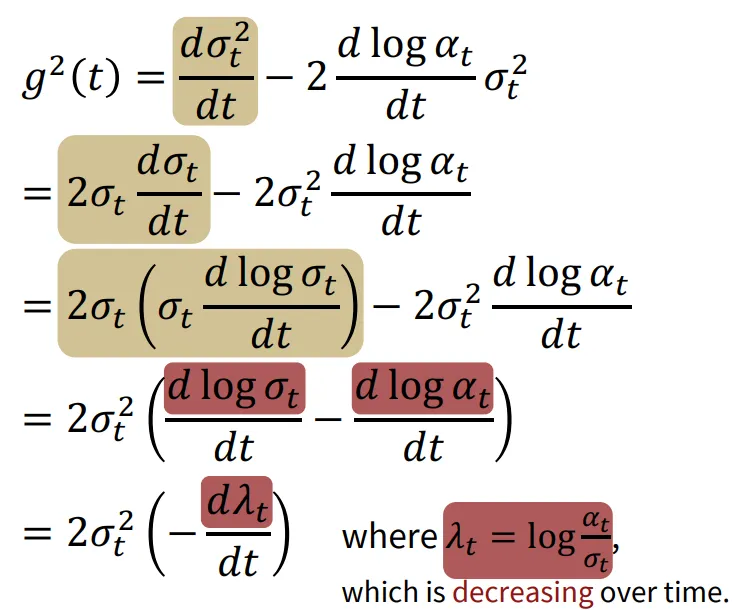
결론적으로 $\lambda_t$라는 변수를 얻게 되고 이는 Signal-to-Noise Ratio(SNR)의 모습에 log를 취한 값입니다.

Variance Preserving (VP) SDE

VP-SED vs VE-SDE

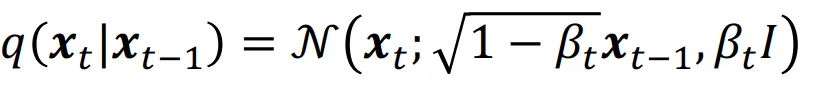
위의 수식은 Vairance Preserving(VP) SDE의 수식입니다. VP-SDE는 데이터 분포에서 시작해 일정한 분산을 유지하면서 노이즈를 추가하는 방식입니다. 노이즈는 $B_t$값에 의해서 결정되는데 초기에서 후기로 갈수록 더 커지지만, 일반적으로 선형 또는 지수적으로 설정됩니다. 평균값도 1 - $B_t$의 루트만큼 감소하게 됩니다. 대표적인 예시로는 DDPM이 있습니다.

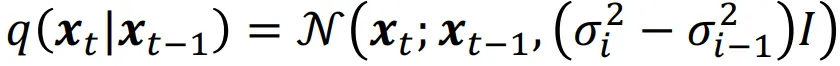
두번째로 Variance Exploding(VE) SDE의 수식입니다. 데이터 분포에서 시작해 시간이 지남에 따라 노이즈의 분산이 폭박적으로 증가하는 방식입니다. 노이즈는 시간 단계 간의 분산 차이로 결정되게 됩니다. 시간이 지날수록 분산이 커지기 때문에 매우 크게 분산이 증가할 것입니다. 평균은 이전 값과 동일하게 갖도록 설정됐습니다.

위의 두 수식 중 VP-SDE의 경우에 대해서 자세히 알아보도록 하겠습니다.

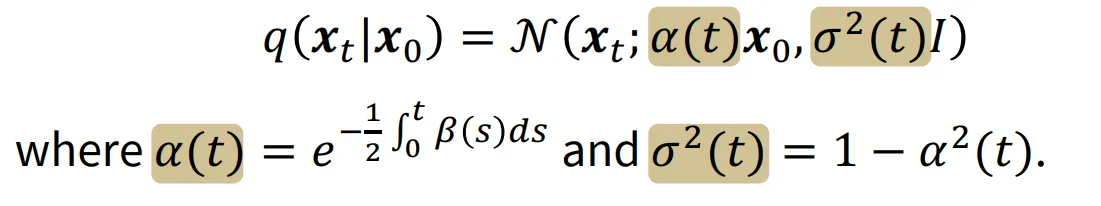
우선 VP-SDE의 수식을 $B_t$가 아닌 스케일을 나타내는 a(t)와 분산을 나타내는 ${\sigma}^2(t)$로 나타냈습니다. 일반적으로 $B_t$는 증가하고, 이를 기반으로 a(t)는 감소, ${\sigma}^2(t)$는 증가하는 것을 알 수 있습니다. 따라서 $a^2(t) / {\sigma}^2(t)$를 나타내는 SNR은 시간이 지날수록 감소합니다.

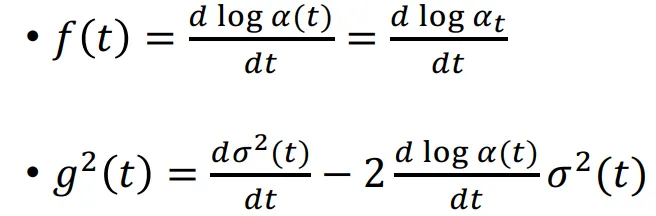
이전에 구한 a(t)와 ${\sigma}^2(t)$를 이용해서 SDE의 수식을 나타내면 최종적으로 아래와 같은 형태가 나올 것 입니다.

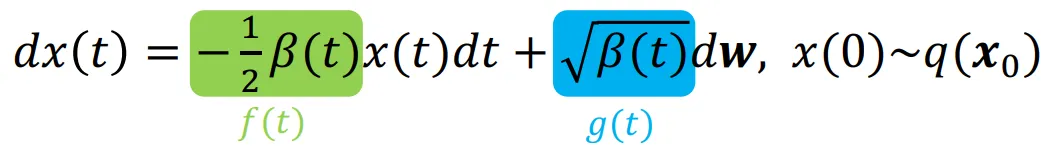
Probability Flow ODE

SDE의 경우 동일한 marginal distribution을 갖는 ODE를 갖습니다(증명은 probability flow ode 논문 참조).

SDE의 Reverse과정은 첫번재 수식과 같고, 이에 대응되는 ODE의 Reverse process는 마지막 줄에 나타난 수식과 같습니다. 위의 수식에서 f(t)와 $g^2(t)$를 이전에 a(t)와 $\sigma(t)$에 대해서 나타난 수식으로 바꾸면 아래의 수식이 나오게 됩니다.

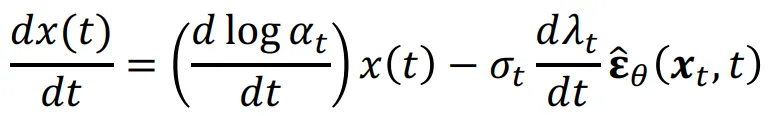
지금 약간 내용들이 중구난방식으로 막 나열 되었는데 한번 정리하고 넘어가도록 하겠습니다.

1. Diffusion 모델을 continuous한 SDE로 바꿀 수 있다.
2. diffusion process SDE는 같은 marginal distribution을 갖는 ODE를 갖는다
3. 따라서 Diffusion 모델을 대응되는 ODE 모델을 수행함으로서 해결할 수 있다.(ODE → SDE → Diffusion)

결론적으로 저희는 ODE를 통해서 Diffusion 모델을 풀 수 있다는 것을 알아보기 위해서 지금까지 열심히 달려왔습니다.

그러면 왜 ODE로 푸는 것이 좋을까요? 바로 ODE를 풀 수 있는 여러가지 방법론이 존재하기 때문입니다. Euler method, Runge-Kutta Method등 여러가지 방법론이 존재합니다.

오늘의 강의 주제는 ODE Solver(푸는 방법)에 관한 것이 아닌, 빠르게 Sampling 한 결과를 얻는 방법입니다. 그러면 오늘 강연에서 ODE Solver중 빠르게 Sampling 하는 방법을 듣는다는 점을 중점적으로 아래 내용을 보시면 이해가 편하실 것입니다.

Ordinary Differential Equation(ODE)

강의 주제에 본격적으로 들어가기전에 ODE의 기본적인 개념부터 배우고 넘어가겠습니다.

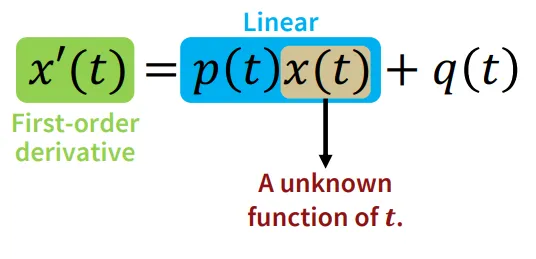
1차 미분의 경우에 대해서 살펴보도록 하겠습니다. 한번만 미분했을 경우 x(t) 와 x’(t)의 최고차항의 계수 차이는 1일 것이고, 이는 위의 식이 어떠한 linear function이라는 것을 알 수 있습니다.

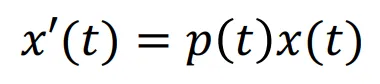
식을 더 단순화해서 q(t)가 0일 경우의 수식은 위와 같습니다. 위의 식에서 양변을 x(t)로 나눠줄 경우 p(t) = x’(t) / x(t)라는 수식이 생성됩니다. 우항은 자세히보면 lnx(t)를 미분한 값이라는 것을 알 수 있습니다.

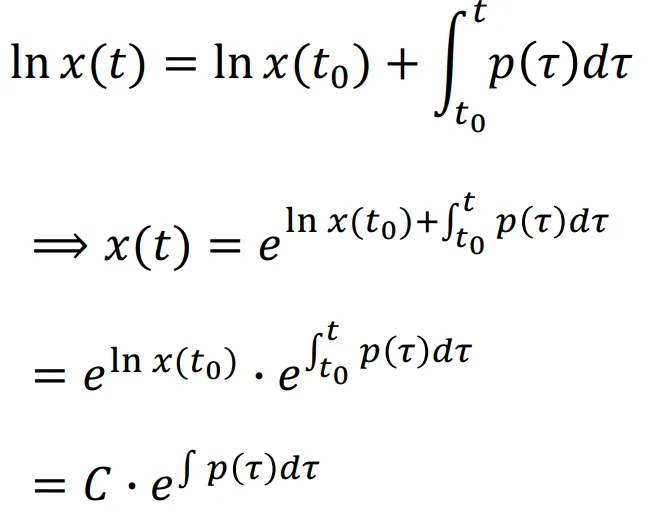
lnx(t)라는 개념을 이용해서 오른쪽 식을 적분하면 위의 수식을 얻을 수 있게됩니다. 위의 전개 과정이 q(t)=0인 정말 단순한 경우의 결과 입니다. 다시 복잡한 일반적인 경우로 돌아가 보겠습니다.

왼쪽에 파란색 부분은 linear하게 풀 수 있지만, 오른쪽 q에 대한 식은 non-linear한 부분이므로 이를 풀기는 어렵습니다. 그러면 이러한 경우에는 어떻게 x(t)를 풀 수 있을까요?

Exponential Integrator

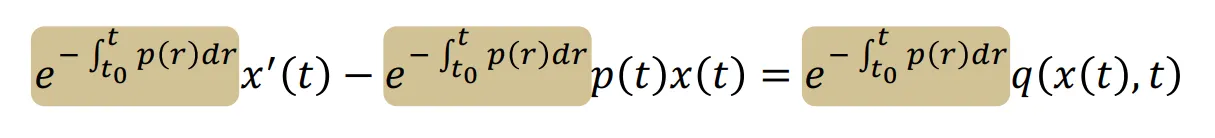
linear한 부분을 좌변으로 옮겨주고, 양변에 똑같이 노란색 부분을 곱해줄 경우 문제가 쉽게 풀린다고 합니다. 이는 경험적으로 구한 하나의 방법이라고 합니다.

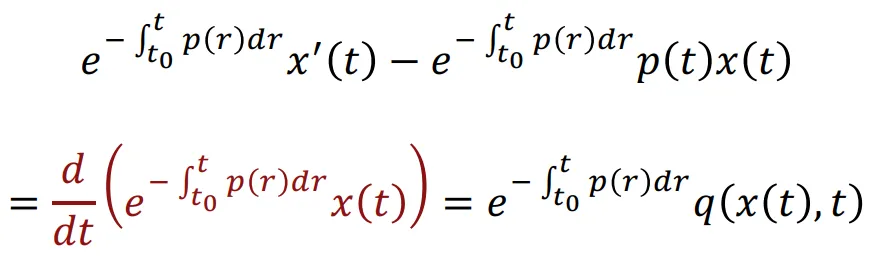
풀이를 조금 더 자세히 설명해드리면 좌변은 빨간색과 같이 하나의 식으로 단순화 할 수 있습니다. $\frac{d}{dt}\Big(p(t)\Big) = q(s) \Rightarrow p(t) = p(s) + \int_{s}^{t} q(\tau) , d\tau$ 라는 힌트를 갖고 아래와 같이 한번 더 나타낼 수 있습니다.

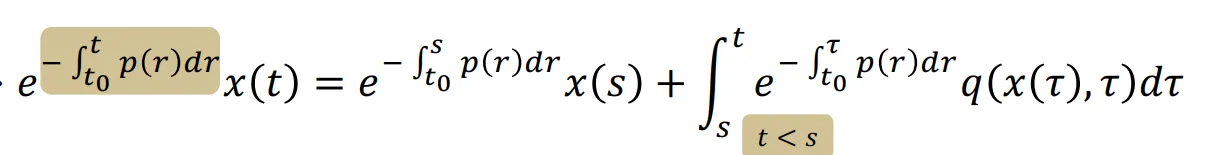
최종적으로 우리가 원하는 형태는 x(t)이기 때문에 양변에 노란색 부분을 나눠준다면 최종적으로 x(t)는 아래와 같은 형태가 될 것입니다.

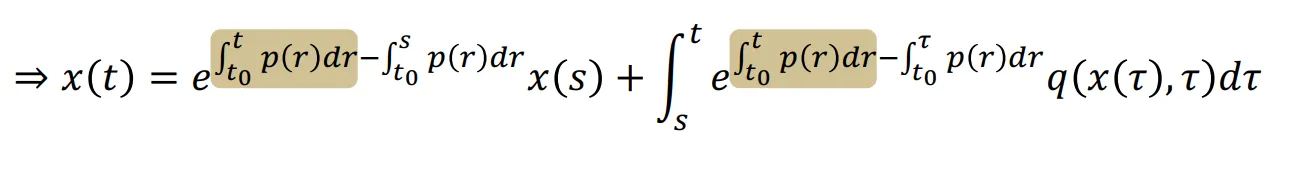
수식들을 자세히 보면 e의 지수승 적분에서 시작 지점은 동일하고, 끝 지점만 t와 s 그리고 t와 r로 다르기때문에 이 적분 부분만 단순화하면 아래의 수식이 나옵니다.

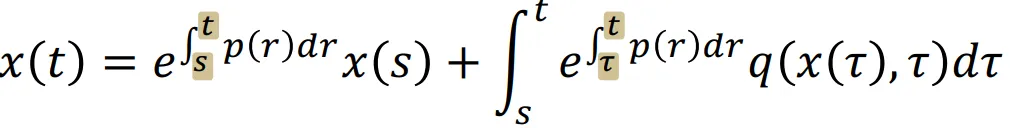
이제 어떠한 형태의 1차 미분 방정식을 풀 수 있는 일반화된 식을 얻었습니다.

DPM-Solver

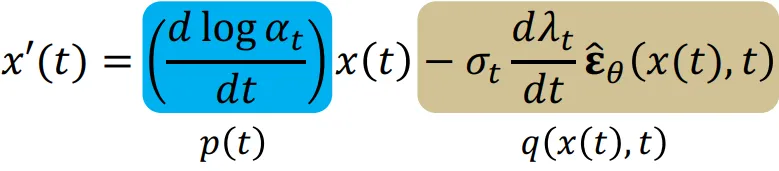
다시 ODE의 개념에서 돌아와서 위의 수식을 보면 파란색 부분은 linear, 노란색 부분은 non-linear 부분이라는 것이라는 것을 알 수 있습니다. 그러면 이전에 ODE를 수학적으로 푸는 일반화 식을 위의 수식에 대입하면 어떻게 될까요?

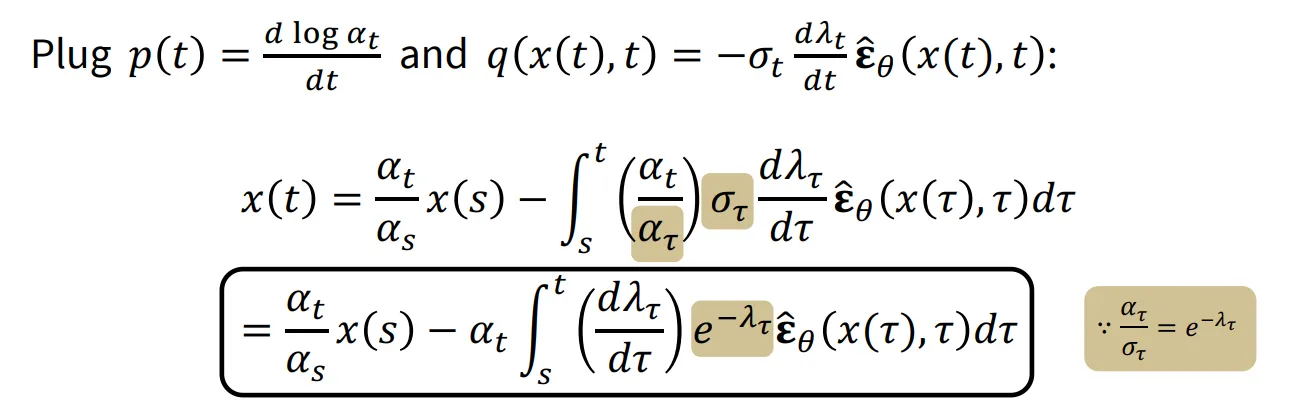
p(t)와 q(t)를 일반화된 ODE를 푸는 수식에 대입했을 때 위의 결과가 나오게 됩니다. 한가지 계산 편의를 위해 $a_r / \sigma_r$를 $\lambda_r$로 정의해서 사용합니다. $\lambda_r$는 SNR 값으로 이전에 시간이 지날수록 감소하는 것을 알 수 있었습니다. 그러면 시간에 대해서 나타내는 것이 아니라, $\lambda_r$에 대해서도 정의할 수 있게 되는데 해당 과정을 나타낸 것이 아래의 식입니다.

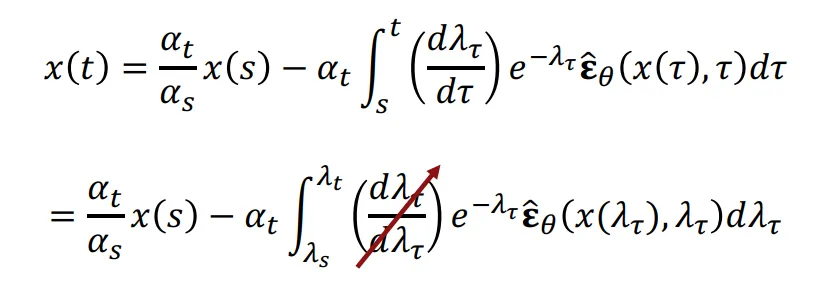
최종적으로 우리가 얻은 continuous ODE의 수식은 위와 같고, 이를 discrete한 버전으로도 바꿀 수 있습니다. Discrete로 바꾼 부분에서 적분 식이 복잡하기 때문에 근사치를 구하고 싶은데, 어떻게 구할 수 있을까요?

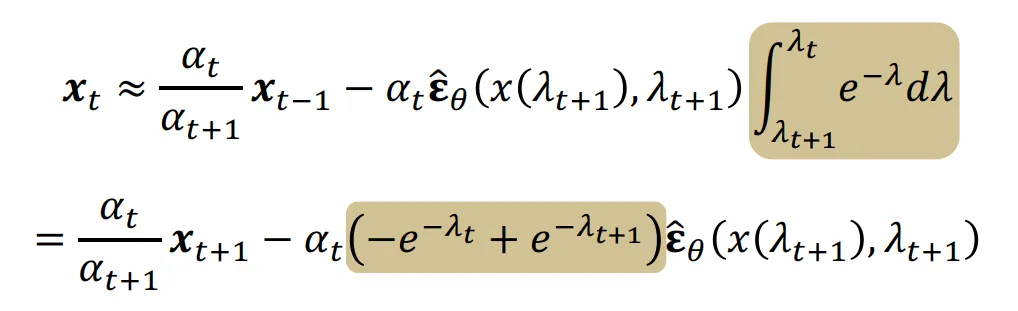
적분 구간에서 $\epsilon_{\theta}$가 constant라고 가정하면, 해당 범위에서의 적분은 아래의 식처럼 나타낼 수 있습니다. 이를 통해서 쉽게 근사치를 구할 수 있습니다.

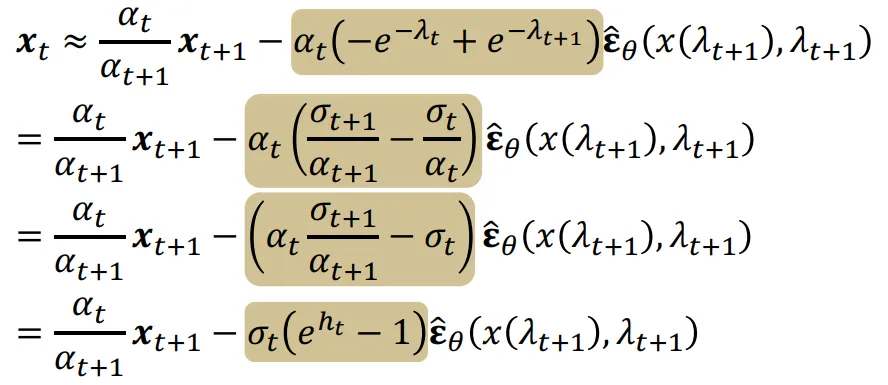
어려운 과정이었지만, 결과적으로 Reverse process를 위의 과정처럼 근사화해서 얻을 수 있고, 해당 근사화 과정에서는 단순한 노이즈 예측한 값에 Scale을 곱해주는 것이 끝인 determinsitic 한 형태입니다.

Determinsitic한 Diffusion 모델이라고 하시면 다들 DDIM을 쉽게 떠올리실 것입니다. 맞습니다 실제로 위의 수식 DPM-Solver-1은 DDIM과 동일한 수식을 갖고 있습니다.

지금까지 모둔 수식을 1차 ODE, 1차 DPM-Solver에 관해서 나타냈습니다. 하지만 2차, 3차처럼 더 높은 차에 대해서도 DPM-Solver가 나타낼 수 있습니다.

DPM-Solver-2의 예시를 들어드리면, 한개의 중간점을 둔 DPM-Solver-1입니다. 더 자세한 내용은 위의 DPM-Solver 논문 리뷰를 참고하시면 됩니다. DPM-Solveer-k로 일반화 한다면 k-1개의 중간점을 갖는 DPM-Solver-1입니다.

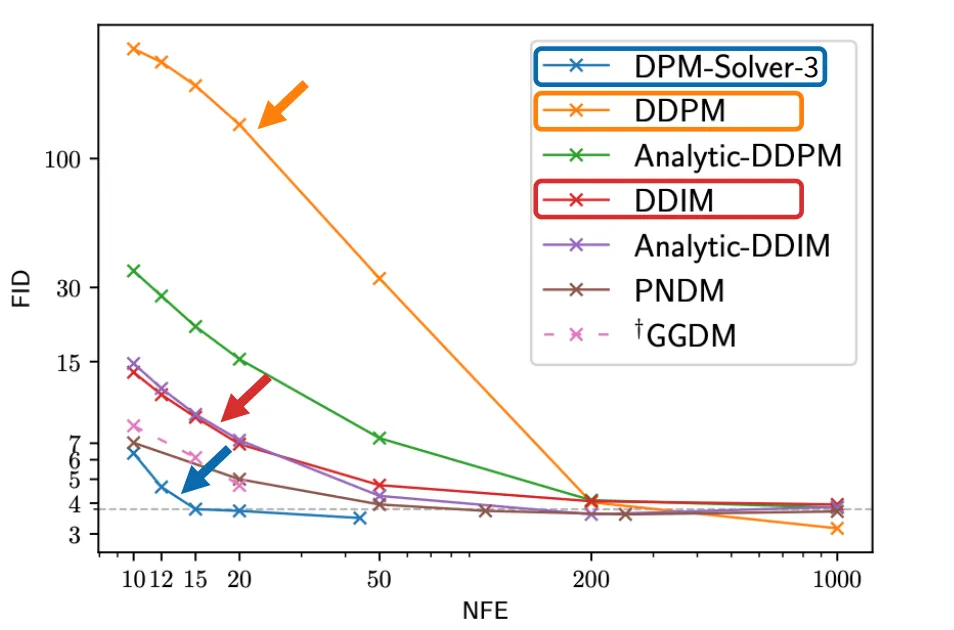
결론적으로 이본 강의의 핵심 내용인 더 적은 step으로도 더 좋은 결과를 내는 모델인 DPM-Solver를 얻게 됐습니다.