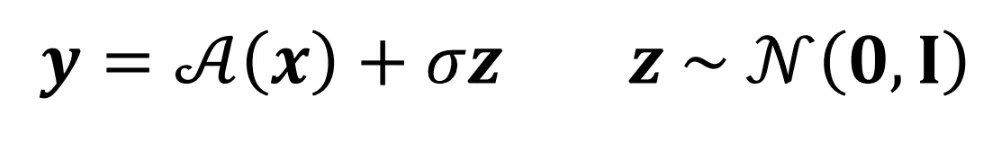
참고: 강의 11은 Diffusion Synchronization와 관련된 내용이고, 적용 분야에 대한 설명이라 생략했습니다.

출처[LECTURE12]
강의 영상 및 자료:
https://mhsung.github.io/kaist-cs492d-fall-2024/
해당 강의를 기반으로 추가적인 설명을 정리했습니다.

Inverse problem

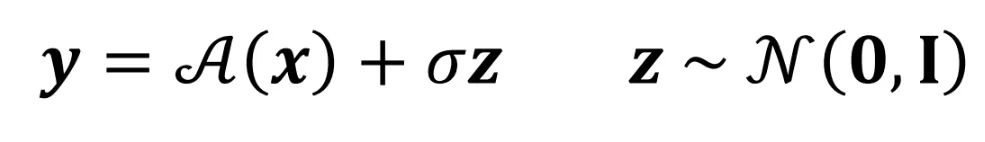
측정값 y로부터 그것을 발생시킨 원인 x를 찾는 것이 Inverse problem입니다. 이때 고려해야할 점은 A(x)라는 함수와 $\sigma z$라는 노이즈 값입니다.

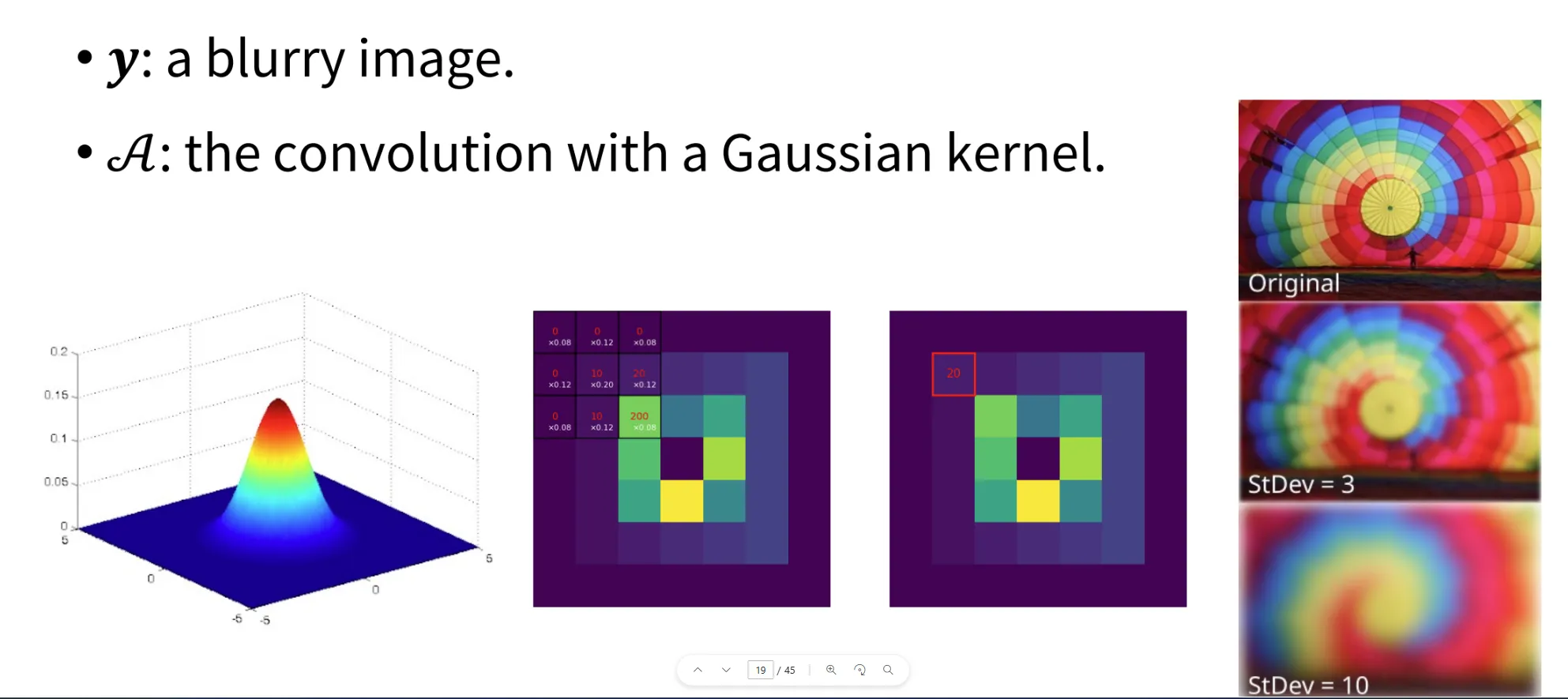
하나의 예시는 blurry한 이미지로부터 원본이미지를 찾는 과정입니다. 관찰된 이미지가 blurry한 이미지이고, A라는 함수가 Gaussian kernel로 왼쪽에 보이는 것처럼 가운데의 가중치가 크고 주변 가중치가 낮은 것 입니다. 해당 방식을 오른쪽 3x3 kernel에 적용하는 방법이 Gaussian kernel을 convolution에 적용한 것입니다.

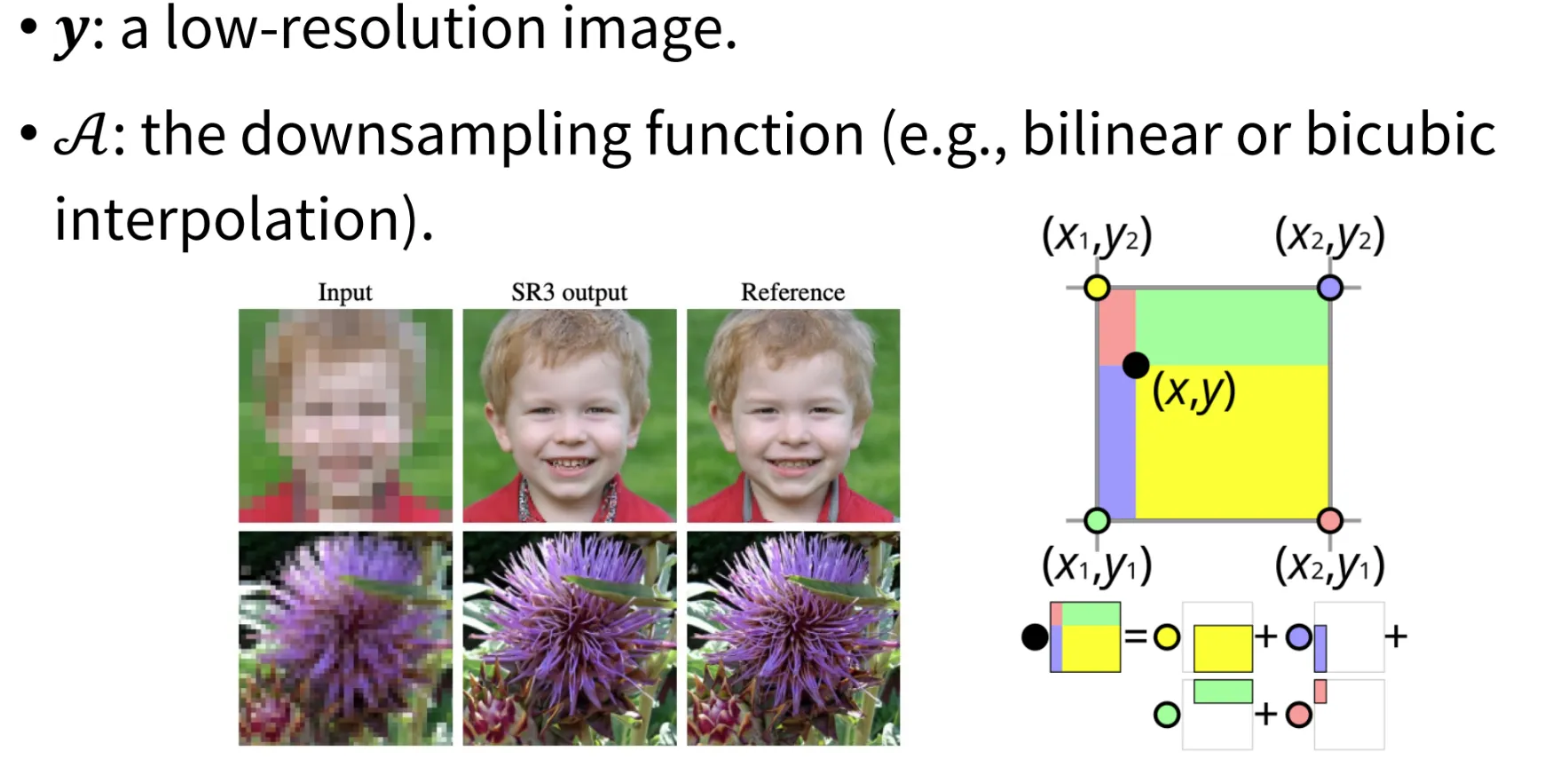
다른 분야는 super-resolution 방법입니다. 입력 이미지로부터 해상도를 높이는 과정을 나타내는 과정도 inverse problem을 통해서 얻을 수 있씁니다.

놀랐던 점은 Inpainting/Outpainting 분야도 inverse problem으로 해결할 수 있다고 합니다. y는 이미지에 우리가 변형하고자 하는 요소가 반영된 결과, A는 이러한 요소들을 바꿔주는 함수, Inpainting/Outpainting 모델이 될 것입니다.

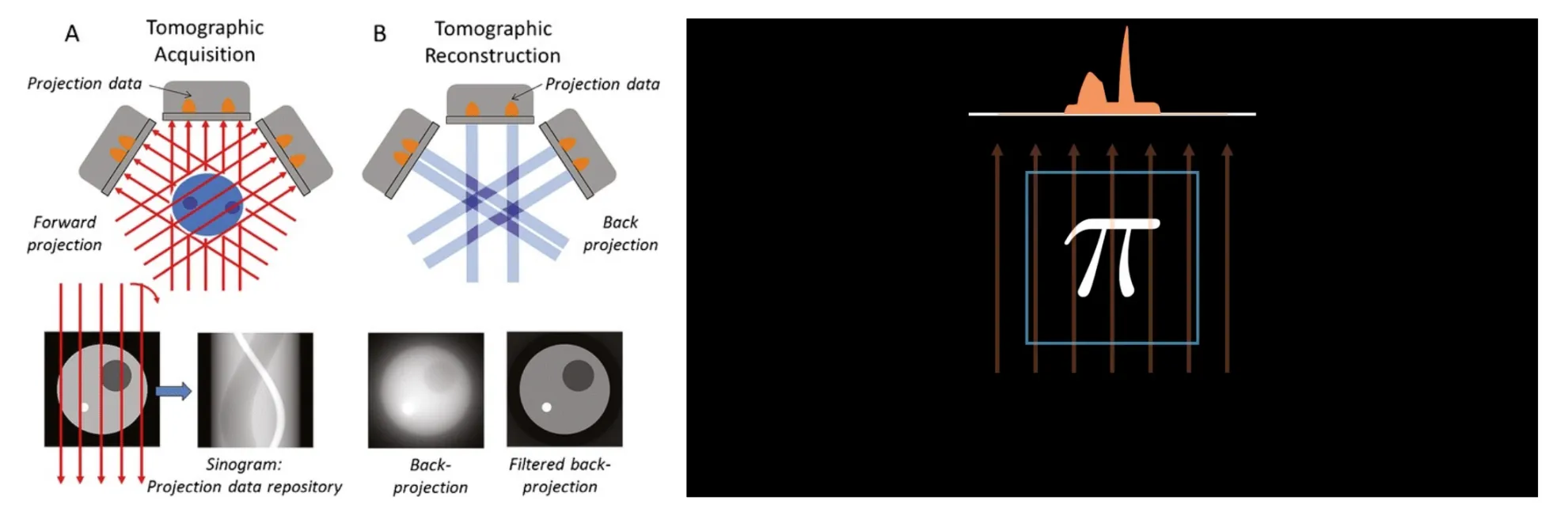
또 다른 분야는 Tomography 입니다. Tomography는 한국말로 단층 촬영으로서 출력 결과(y)는 projection된 결과 이미지이고, 함수 A는 projection 과정입니다.

이러한 것처럼 Inverse problem은 다양한 분야에서 사용되고, 많은 Solution이 존재합니다. 따라서 Conditional generative model이 필요하게 된 것입니다.

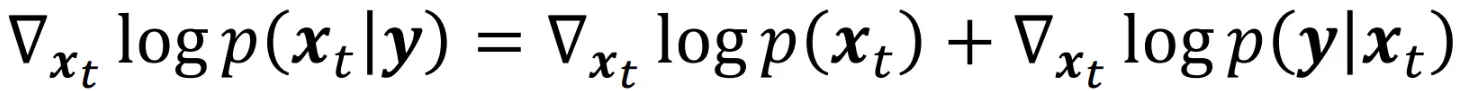
$\nabla_{x_t} \log p(x_t)$를 학습했을 때 $\nabla_{x_t} \log p(x_t|y)$는 어떻게 구할 수 있을까요? Guidance쪽 강의를 들으셨던 분들이면 쉽게 아실 수 있을 것입니다. 위의 수식처럼 베이즈 정리를 이용하면 $y|x_t$로 쉽게 변형해서 구할 수 있습니다.

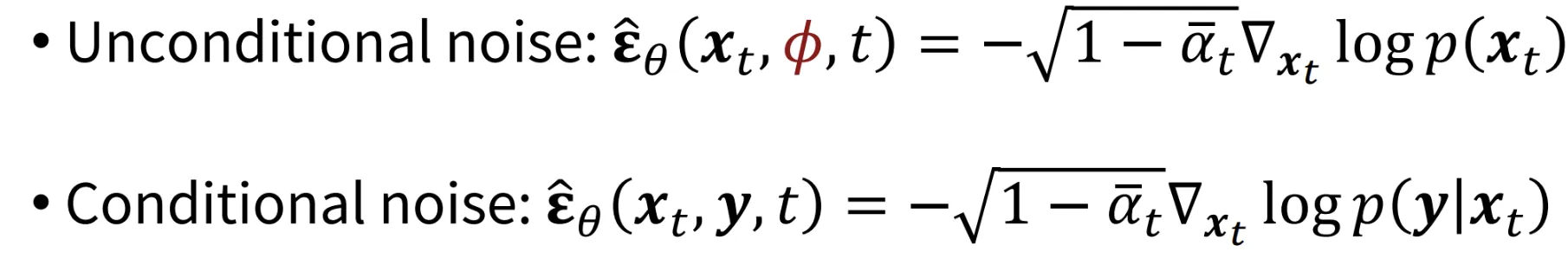
복습하는 겸 수식을 가져오면 Classifier-Free Guidance의 수식은 위와 같습니다. 이때 $\nabla_{x_t} \log p(y|x_t)$는 t에서의 확률 분포 $x_t$가 y라는 label에 따라 어떻게 변하는지를 나타내는 값입니다. 이를 기반으로 이전 사진의 수식 $\nabla_{x_t} \log p(x_t)$를 구할 수 있습니다.

Pseudoinverse-Guided Diffusion Models (ΠGDM)

Classifier Guidance의 Conditional noise 부분에서 $\nabla_{x_t} \log p(x_t)$를 학습을 이용해서 구했는데, 학습 없이 진행할 수 있는 방법에 대해서 이야기한 논문입니다.

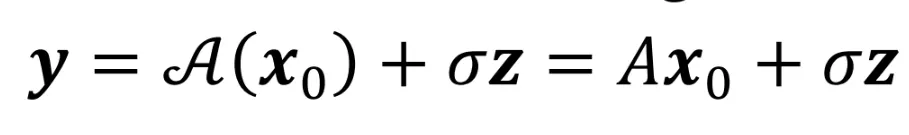
우선 간단하게 A라는 함수가 linear 함수라고 가정하고 진행하도록 하겠습니다. 앞으로의 과정이 수식적인 부분이 많아서 결론만 보시고 싶은 분은 생략하고 넘어가셔도됩니다.

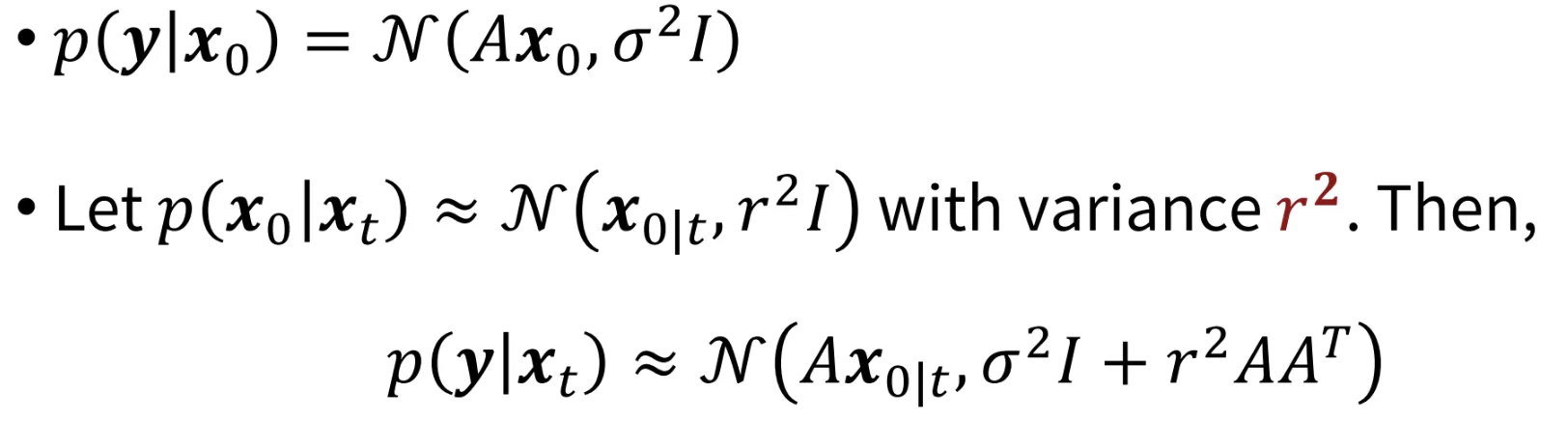
첫번째 수식과 두번째 수식을 연결하면 3번째 수식이 되는 것을 확인할 수 있습니다. 두 분포를 더할 때 연결방식은 이전 강의에서도 배웠는데, 평균은 연결한다고 생각하면 되고, 분산들은 그냥 더해주면되는데 $r^2$이 $r^2AA^T$로 바뀐 이유는 linear 함수인 경우 분산이 바뀔 수 있어 $AA^T$를 취해줘야된다고 합니다(해당 개념은 설명해주지 않으셔서 그냥 넘어갔습니다).

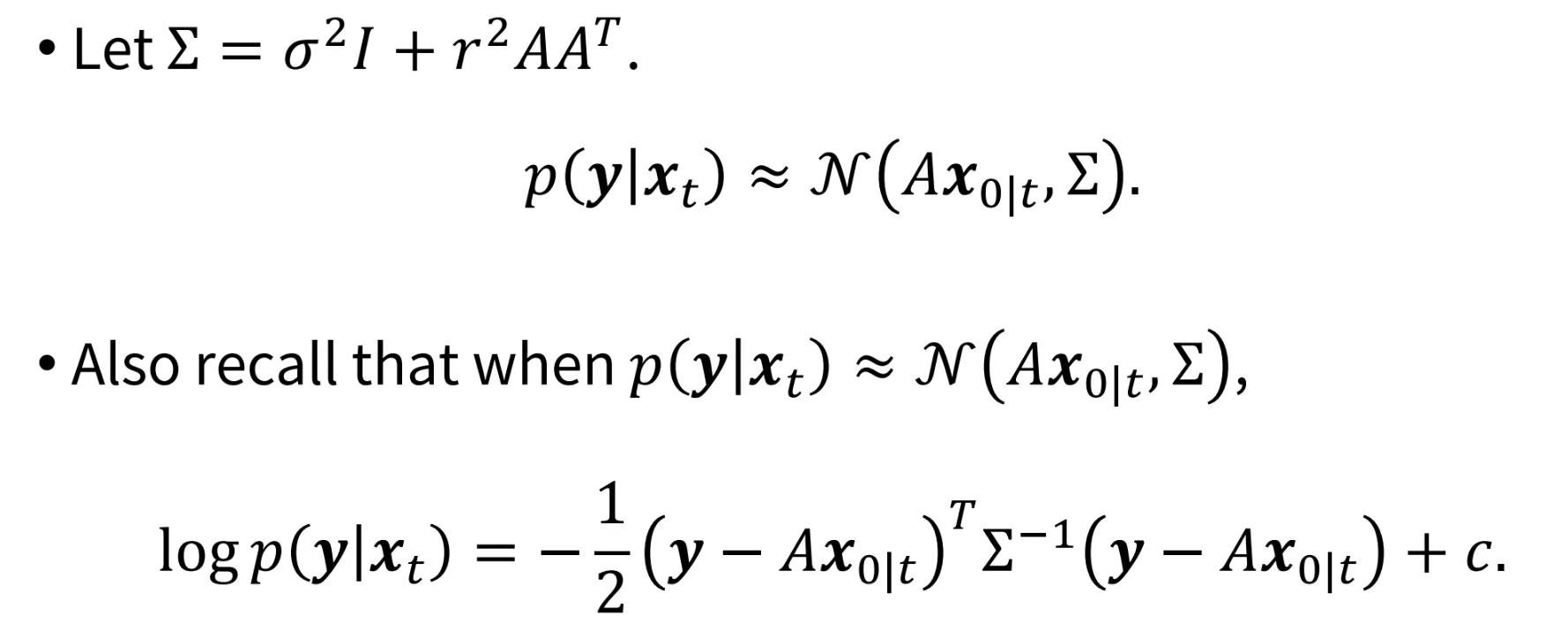
분산을 Σ라고 칭하고 가우시안 식으로 정리하면 위의 사진 마지막 줄이 됩니다.

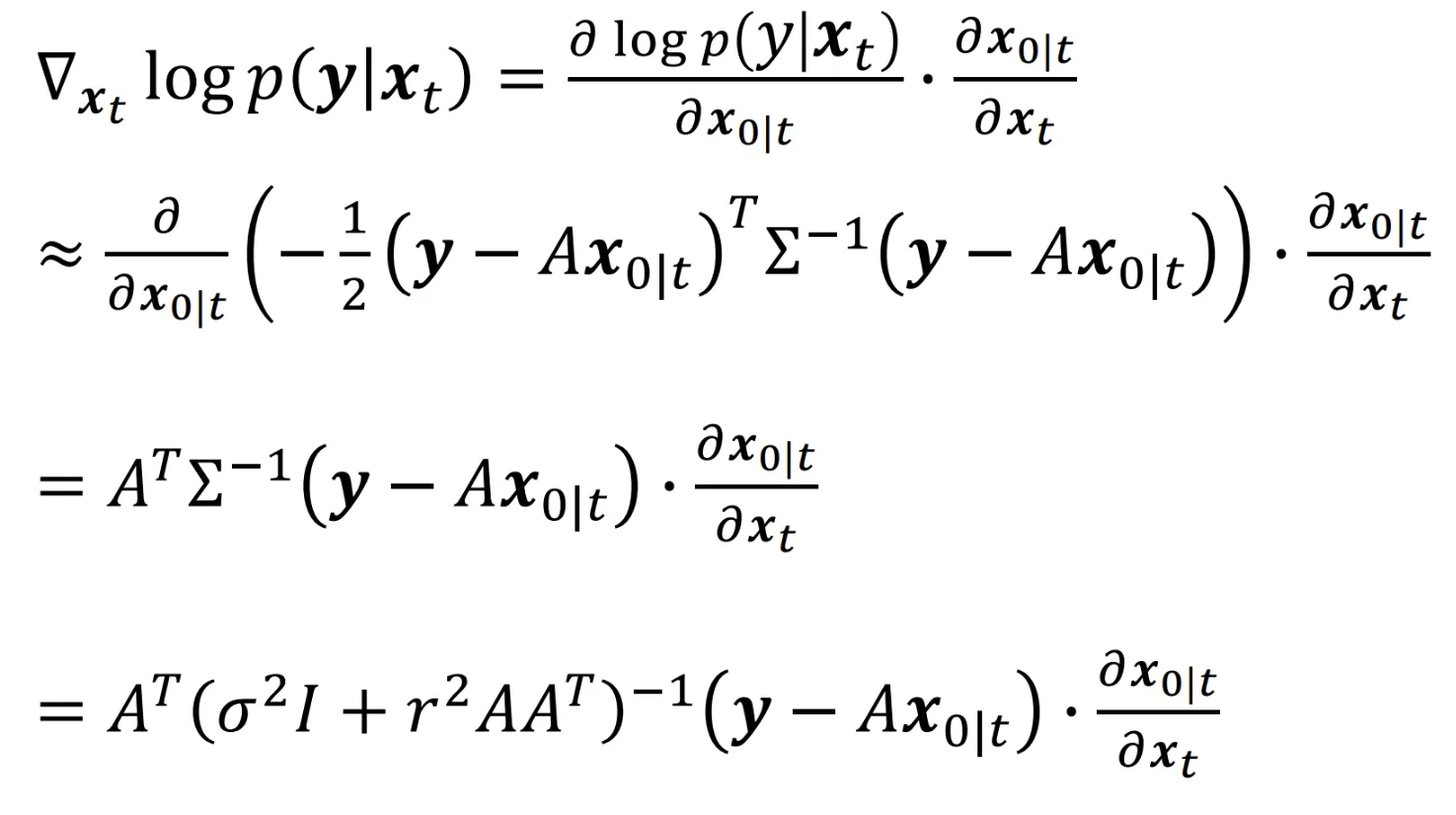
이를 chain rule을 이용해서 미분하고 최종적으로 정리하면 다시 맨 아래의 수식이 나타나는 것을 알 수 있습니다.

이때 분산이 0이라면, 즉 deterministic 하다면 최종식은 위와 같습니다.

조금더 간단하게 하기위해서 $r^2=0$으로 하면 어떤 식이 나올까요? 우선 $r^2=0$이라는 것은 zero variance이고 이는 Dirac delta function이라고 합니다.

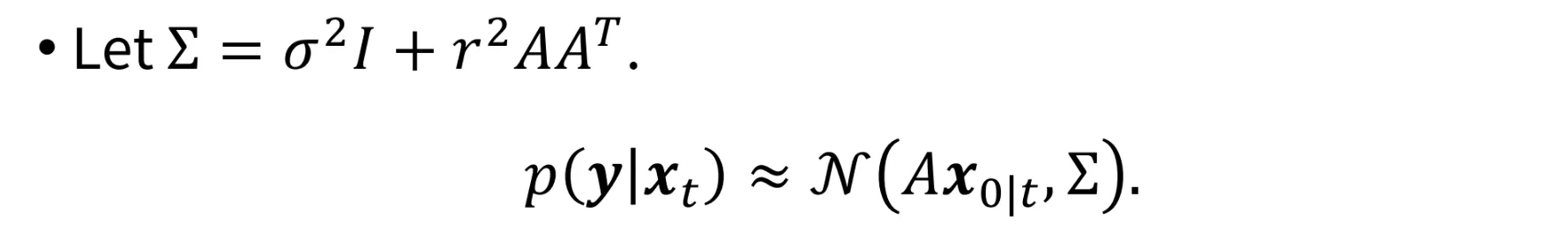
이전에 분산이 위와 같은 형태인데 $r^2=0$인 경우 평균은 똑같고 분산은 $\sigma^2I$일 것입니다.

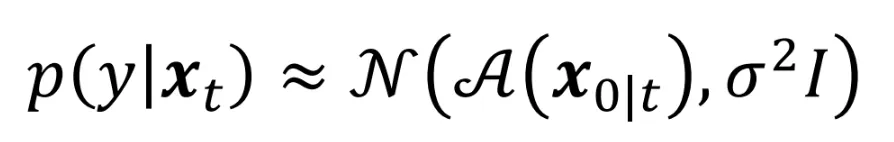
이제 분산이 간단한 형태로 나타났기 때문에 linear function이라는 가정이 없어도 충분히 해결할 수 있을 것입니다.

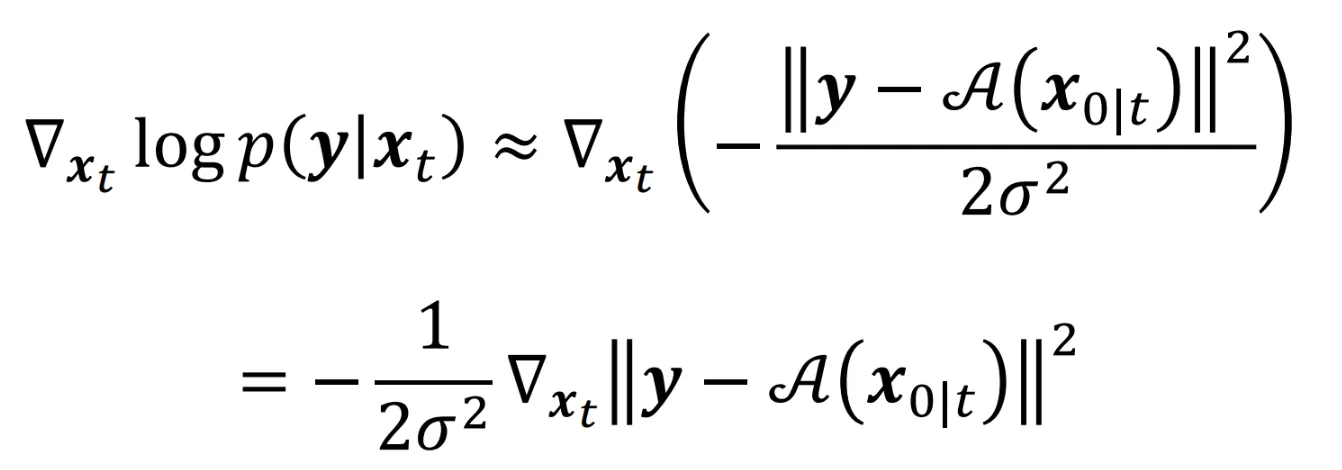
결론적으로 수식은 위의 사진처럼 나타나게 됩니다. 최종 수식을 보면 L2 Difference와 관련된 꼴로 나오게 되는 것을 확인할 수 있습니다.

Diffusion Posterior Sampling(DPS)

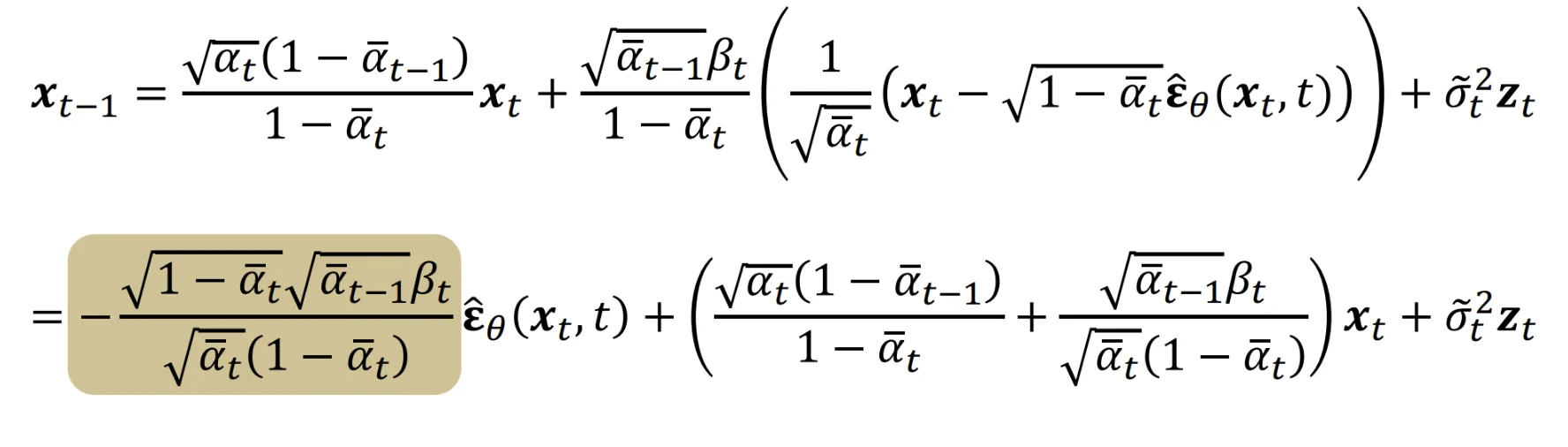
위의 수식은 DDPM의 $x_{t-1}$을 구하는 과정을 나타낸 것입니다. 갑자기 확 나와서 헷갈리신 분들을 위해서 이전 강의에서 배웠던 DDPM 부분을 아래에 붙여놨습니다.

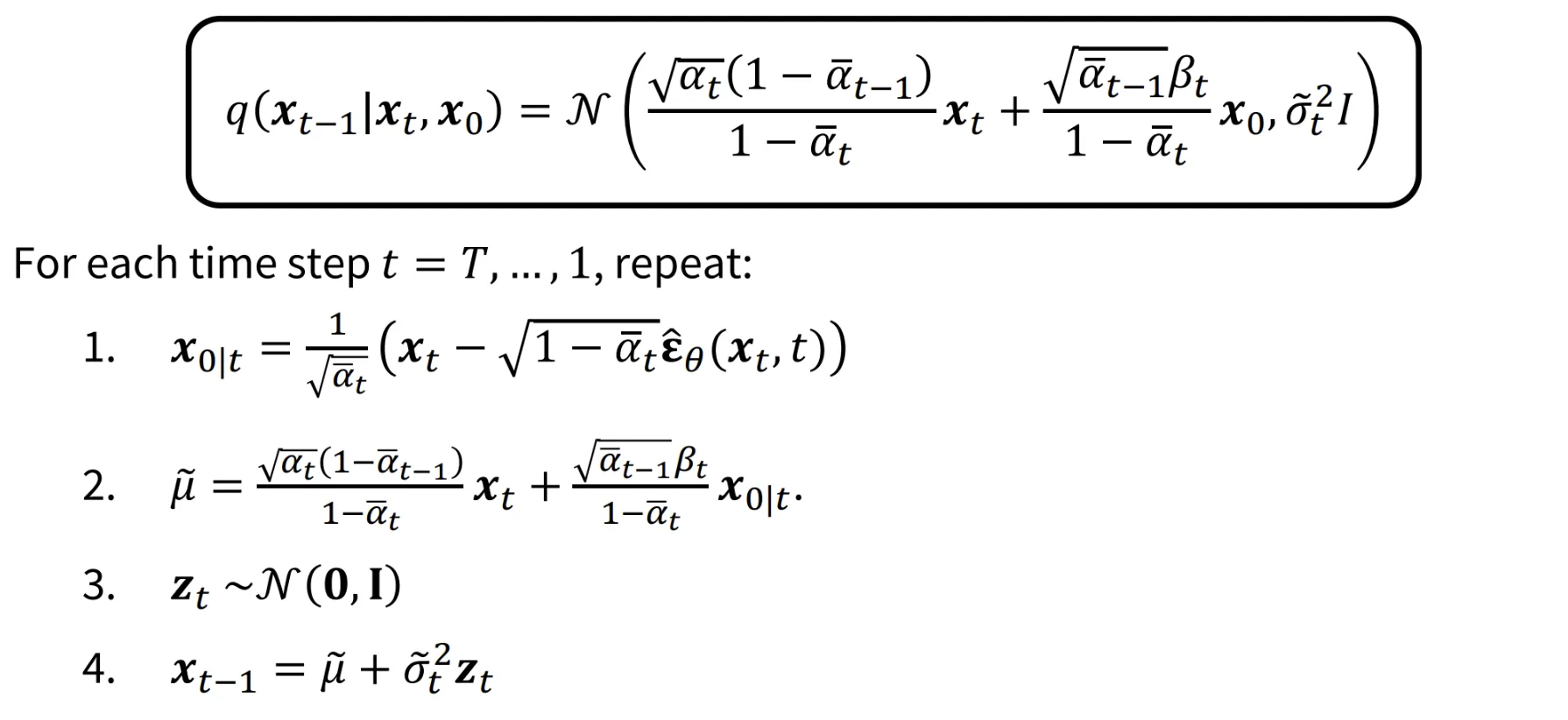
4번의 수식에 1,2,3을 대입하면 이전에 얻었던 식을 얻을 수 있습니다. 결론적으로 $x_{t-1}$은 노이즈 예측에 어떠한 scale값을 곱하고 offset을 붙인 affine function 형태인 것을 알 수 있습니다. 현재 노이즈 예측은 $\epsilon_{\theta}(x_t,t)$에 대해서 나타나있는데 여기서 $\epsilon_{\theta}(x_t, y, t)$처럼 condition 정보까지 추가한 식으로 변경하면 어떻게 될까요?

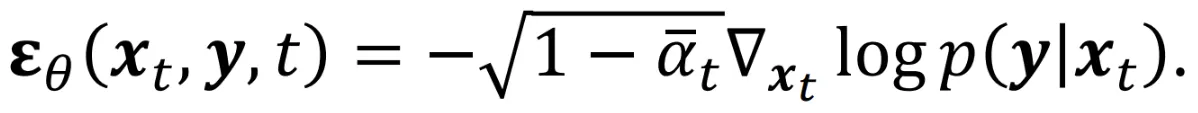
위의 수식을 참고해서 계산한다면 쉽게 구할 수 있을 것입니다.

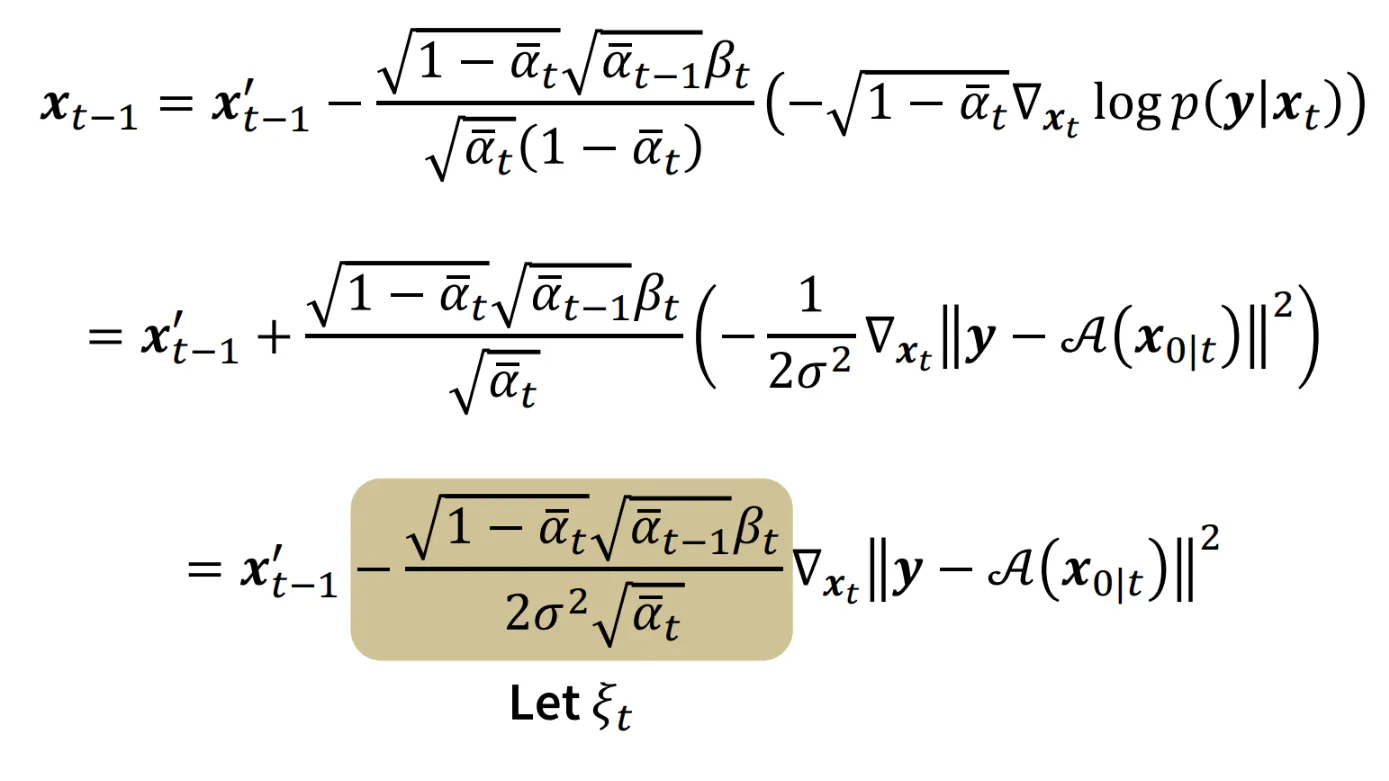
$x^’_{t-1}$은 이전에 저희가 구했던 t-1시점에서 $\epsilon_{\theta}(x_t,t)$의 예측 결과입니다. 나머지 부분을 수식을 따라가면 최종적으로 맨 아래의 수식이 나오는 것을 알 수 있습니다. 결과적으로 scale을 고려하지 않는다면 여기서도 L2 difference의 수식을 이용해서 계산할 수 있을 것입니다.

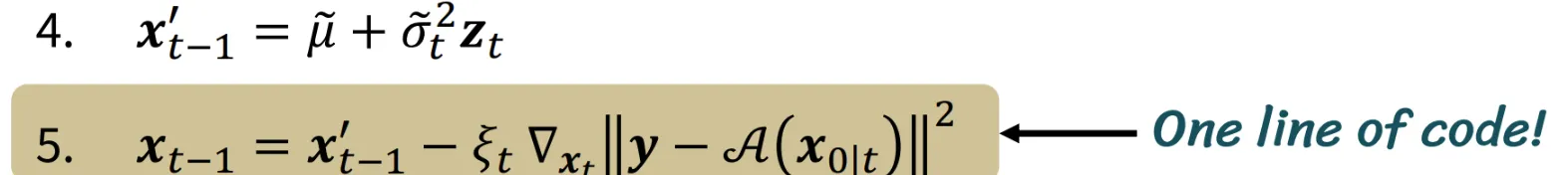
결론적으로 기존 DDPM 논문에서 하나의 코드만 추가하면 Condition이 반영된 정보를 쉽게 구할 수 있는 것을 알 수 있습니다.

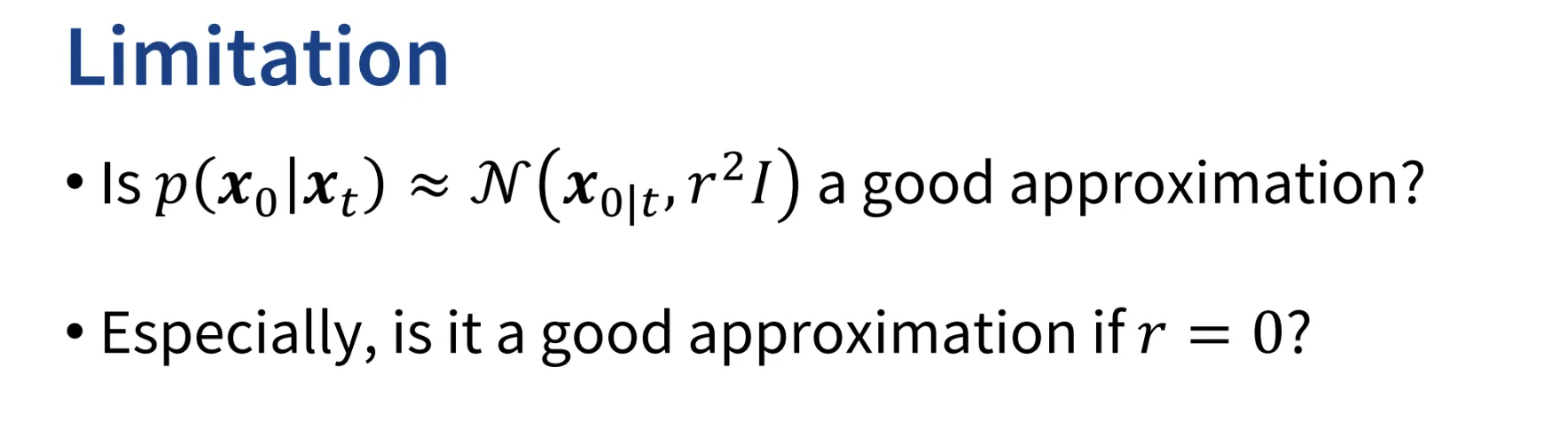
하지만 2가지 한계? 의문? 이 있을 것입니다. 우리가 $p(x_0|x_t)$를 정규분포로 나타냈는데 이게 과연 적절한 근사인가? 와 $r^2=0$으로 설정했는데 이거는 추정 오차가 없다는 말이랑 같은데 이 근사화도 적절한가? 라는 의문이 생길 것입니다. 이러한 의문과 함께 이번 강의가 끝났습니다.