출처[LECTURE10]
강의 영상 및 자료:
https://mhsung.github.io/kaist-cs492d-fall-2024/
해당 강의를 기반으로 추가적인 설명을 정리했습니다.

Score Distillation Sampling(SDS)

지난시간에 배운 내용입니다. 3D Representation에서 사용되는 Score Distillation Sampling(SDS)의 수식입니다.

Connection Between DDIM Reverse Process and SDS

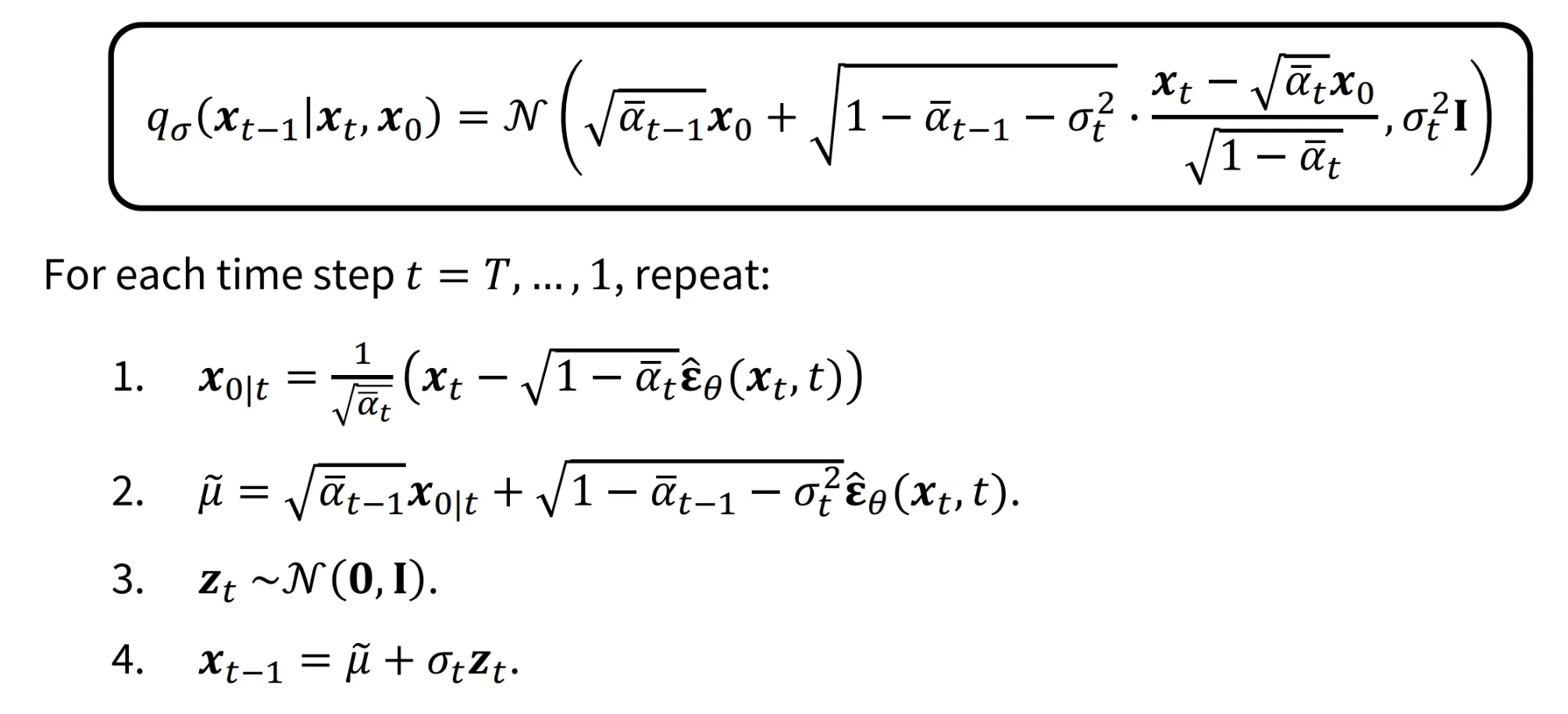
위의 수식은 강의에서 수도 없이 나온 DDIM의 Reverse process에 관한 수식들입니다.

만약에 Maximum Variance를 하고 싶다면 $\sigma_t$값을 어떻게 정해야할까요? 이전에 설명해주셨지만 다시한번 말씀 드리자면, $\sqrt{1 - \bar{\alpha}_{t-1} - \sigma_t^2}$에서 루트 안의 값이 0보다 커야하기 때문에 $\sigma_t$의 값은 $\sqrt{1-\bar{\alpha}_{t-1}}$을 넘을 수 없습니다. 따라서 $\sigma_t$의 최댓값은 $\sqrt{1-\bar{\alpha}_{t-1}}$입니다.

$\sigma_t$값이 $\sqrt{1 - \bar{\alpha}_{t-1} - \sigma_t^2}$일 때 SDS가 어떻게 동작하는지 확인해보록 하겠습니다.

1. view c에서의 렌더링된 이미지를 구합니다.
2. 가우시안 분포로부터 $z_t$를 가져옵니다.
3. $x_{t-1}$의 값을 $x_{0|t}$로부터 구합니다.
4. 이후 다시 $x_{t-1}$에서 노이즈를 제거한 $x_0$를 구합니다.
5. 방금 구한 $x_0$를 기반으로 렌더링 network의 $\theta$를 업데이트합니다.

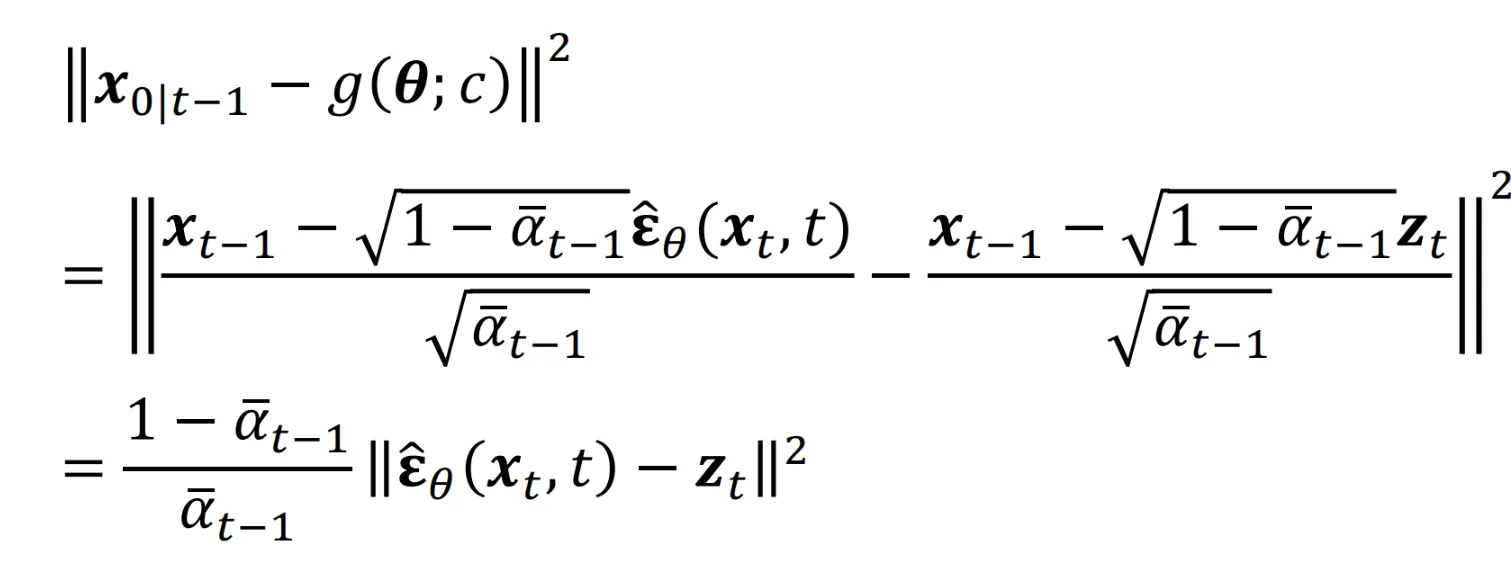
결과적으로 위의 과정을 왜했냐면 SDS를 구하는 Loss Function은 Diffusion 모델과 동일하게 작동하는 것을 보여주려고 했습니다. 맨 아래의 결과를 보면 결국 노이즈를 예측하는 과정에 scale factor만 추가된 것을 알 수 있습니다.

Score Distillation via Inversion(SDI)

위의 과정들에서 $\sigma_t$가 Maximum variance를 갖을 때 어떻게 SDS가 나타내는지 확인했습니다. 하지만 DDIM의 장점중 하나가 deterministic 하다는 점인데 Maximum variance는 이에 해당 하지 않으니, $\sigma_t$를 0으로 설정해서 deterministic하게 했을 때 어떤 결과가 나오는지 확인해 보겠습니다.

$\sigma_t$를 0으로 설정했을 때 어떤 문제가 있을까요? $\sigma_t$가 0이라는 것은 deterministic 하다는 것이니까 $x_t$의 값이 매번 똑같습니다. 하지만 $x_t$의 값은 랜덤한 view c에 따라서 바뀌어야 합니다. c는 랜덤적인데 $x_t$는 고정적이라서 불안전한 결과가 나오게 됩니다.

이에 대한 해결책으로 지난 강의에서 배운 Inversion이 나오게 됩니다. 이렇게 되면 view c가 바뀌더라도 해당 $x_0$로 부터 $x_t$를 DDIM Inversion을 통해서 다시 구할 수 있기 때문에 deterministic하면서도 $x_t$를 view c에 따라서 구할 수 있게 됩니다.

Extension to Editing

왼쪽에 있는 사진을 입력으로 넣고 SDS를 계속 돌리면 오른쪽의 결과가 나타난다고 설명해주셨습니다. 딱 보면 text prompt와는 적절하게 매칭되지만 identity를 잃었다고 해도 과언이 아닙니다.

Delta Denoising Score

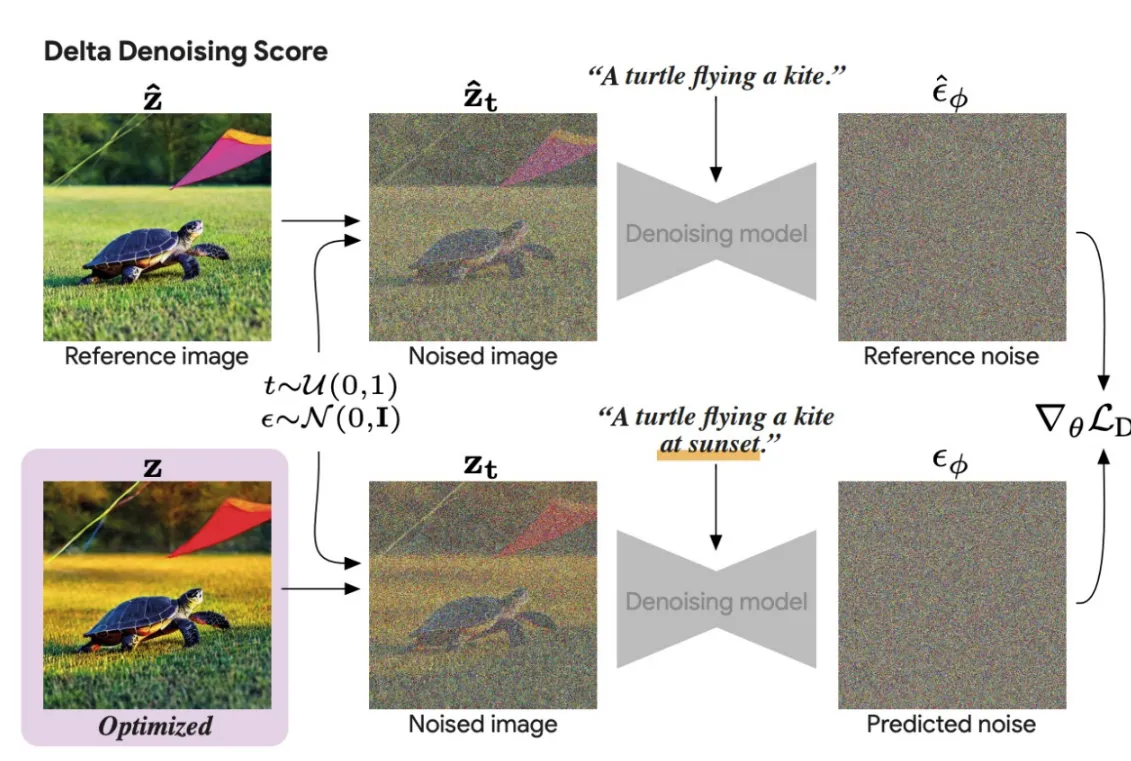
위의 한계를 극복한 방법이 Delta Denoising Score 방식입니다.

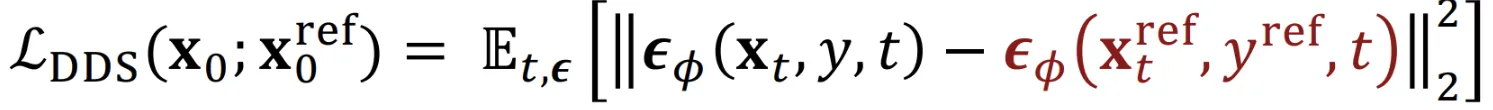
수식을 보면 확실히 이해하시기 쉬우실겁니다. Reference image가 윗줄에 줄어져있고, 이를 기반으로 우리가 학습하고자 하는 이미지를 만듭니다. 이때 Reference이미지의 노이즈 예측값과 차이를 최소화하는 형식으로 노이즈를 예측해서 identity를 잃지 않도록 하는 것입니다. 개인적으로 이 과정은 이전 강의에서 설명해주신 Null-Text prompt의 역할과 비슷하다고 생각했습니다.

하지만 DDS도 결국 identity를 잃는다는 결론이 있습니다.

Posterior Distillation Sampling

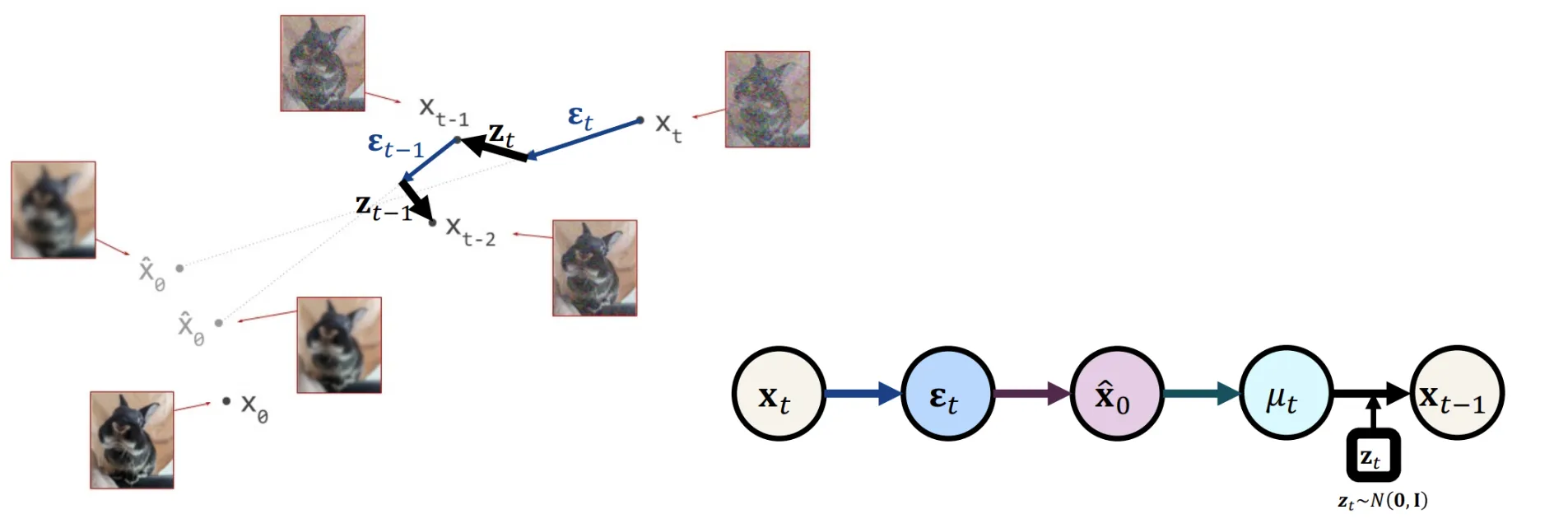
핵심적인 아이디어는 경로에서 단순히 노이즈를 예측하는 것에서 끝나지 않고 $z_t$를 더해주는 과정을 나타내 줌으로써 더 정확한 경로를 찾을 수 있도록 합니다.

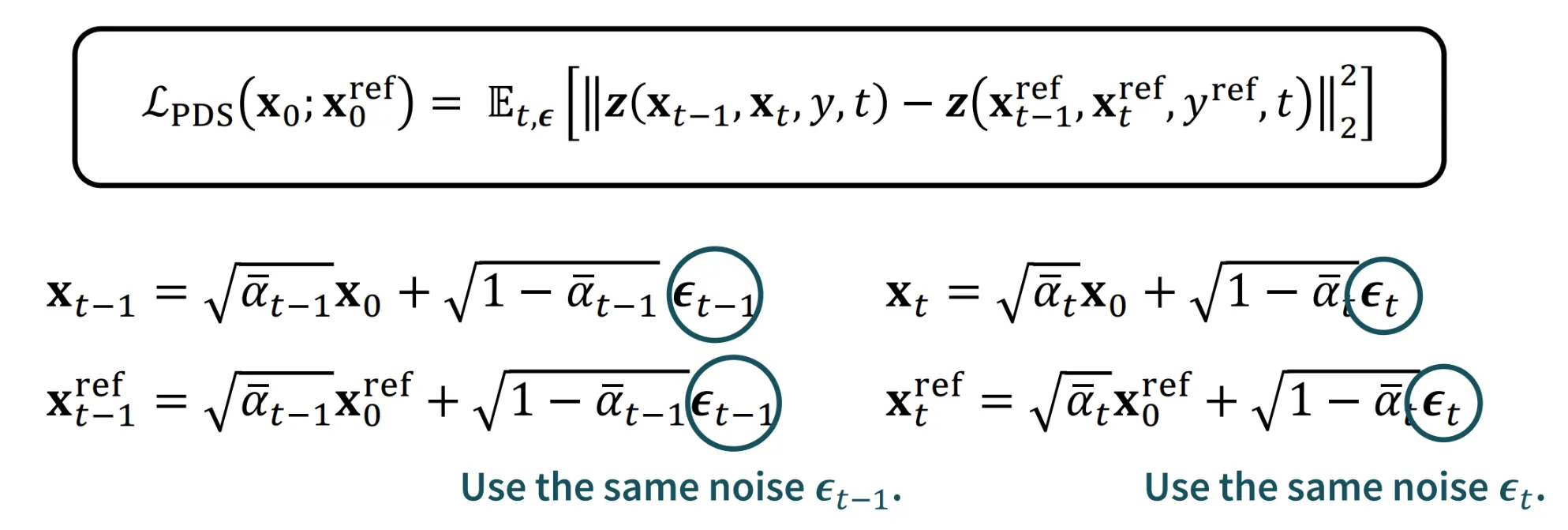
$x_t$와 $x_{t-1}$로부터 $z_t$를 예측할 수 있도록 모델을 설계해서 더 정확한 경로로의 이동을 합니다. 자세한 내용은 논문을 참조해야될거 같습니다.

Comparative Anaysis Editing Process

지금까지 배운 Editing Process들의 차이를 간단히 시각화해서 알아보도록 하겠습니다. 위의 빨간색 점들이 class label 1에 속하는 데이터 점들, 파란색 점들이 class label 2에 속하는 데이터 점들입니다. 빨간색 데이터 하나를 파란색으로 수정하고 싶을 때 각각의 Editing Process들이 어떻게 진행되는지 설명해드리겠습니다.

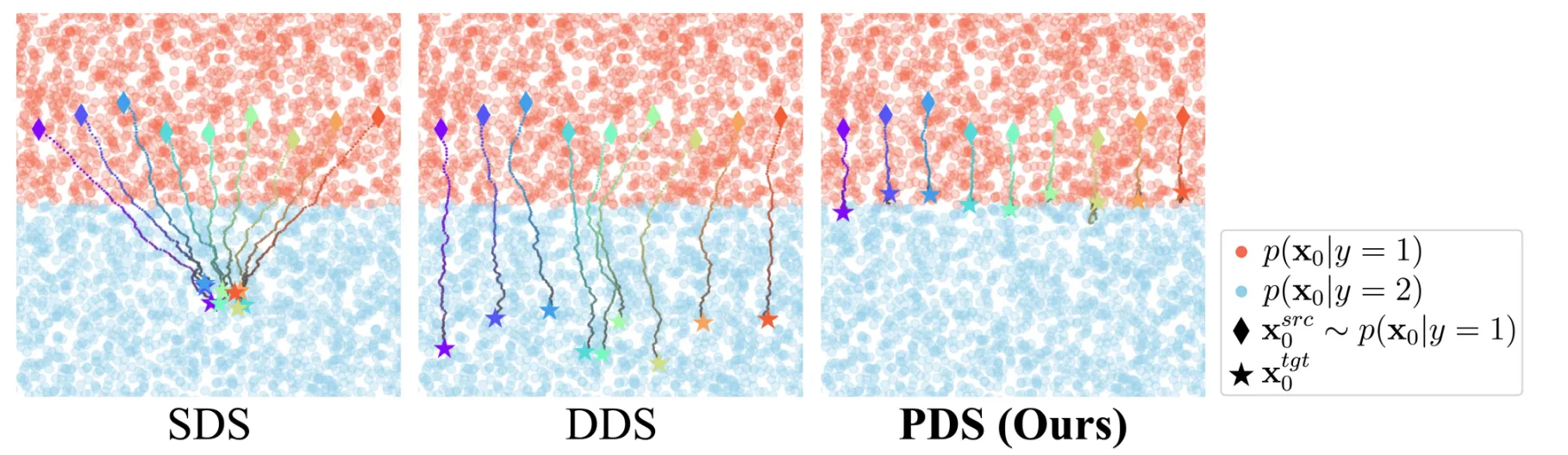
SDS: 하나의 파란색 데이터로 몰리게 됩니다. (Mode Collapse)

DDS: 빨간색 점들로부터 너무 멀어진 결과가 나옵니다. (입력 이미지 정보 손실)

PDS: 빨간색 점들로부터 가장 가까운 파란색 점으로 이동합니다.

PDS 수식을 보면 Identity preservation term이 존재하기 때문에 더 좋은 결과가 나왔다고 언급했습니다.