좌표계
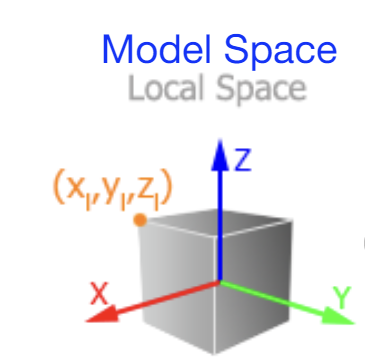
Model Space
객체 자체의 로컬 좌표계
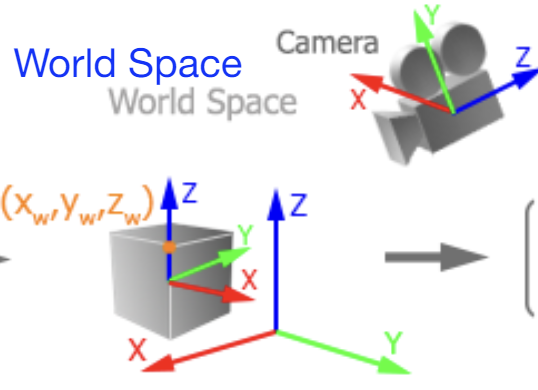
World Space
모든 객체가 배치되는 공통의 글로벌 좌표계
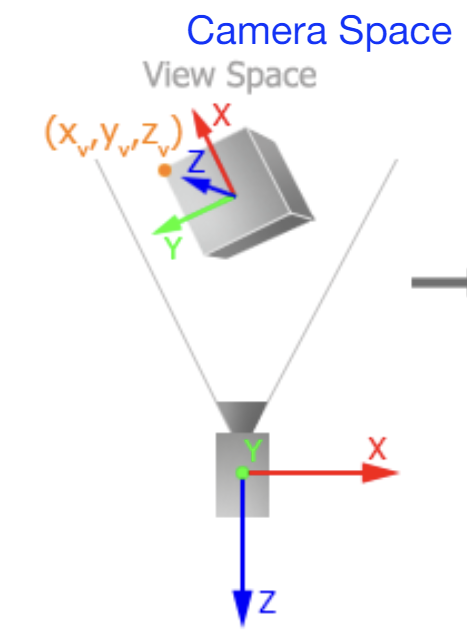
Camera Space
카메라의 관점에서 어떻게 보이는지를 정의하는 좌표계
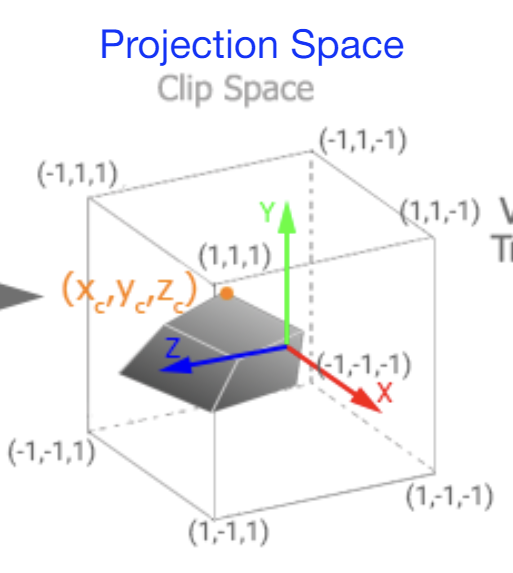
Projection Space
카메라 공간의 객체를 2D 화면에 투영하는 좌표계
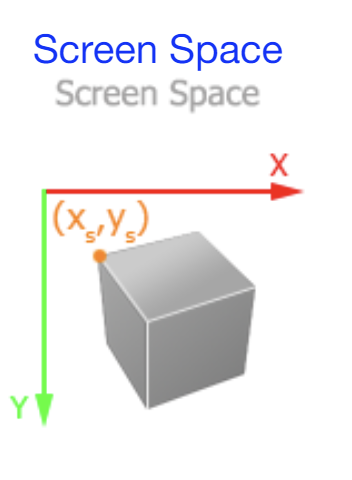
Screen Space
객체가 화면에 그려지는 좌표계
좌표 변환(Transformation)
Model -> World (Xwm) "World Transformation Matrix"
Homogeneous Matrix
4차원 좌표계(x, y, z, w) → 3차원 좌표계 (x′,y′,z′) (x′=x/w,y′=y/w,z′=z/w)
- Homogeneous Matrix를 사용하면 변환(Rotation, Translation, Scale, Projection)을 하나의 행렬로 통합하여 처리할 수 있다

World -> Camera (Xcw) "View Matrix"
Camera -> World를 구하고 역행렬로 나타내자!
정해줘야하는 값
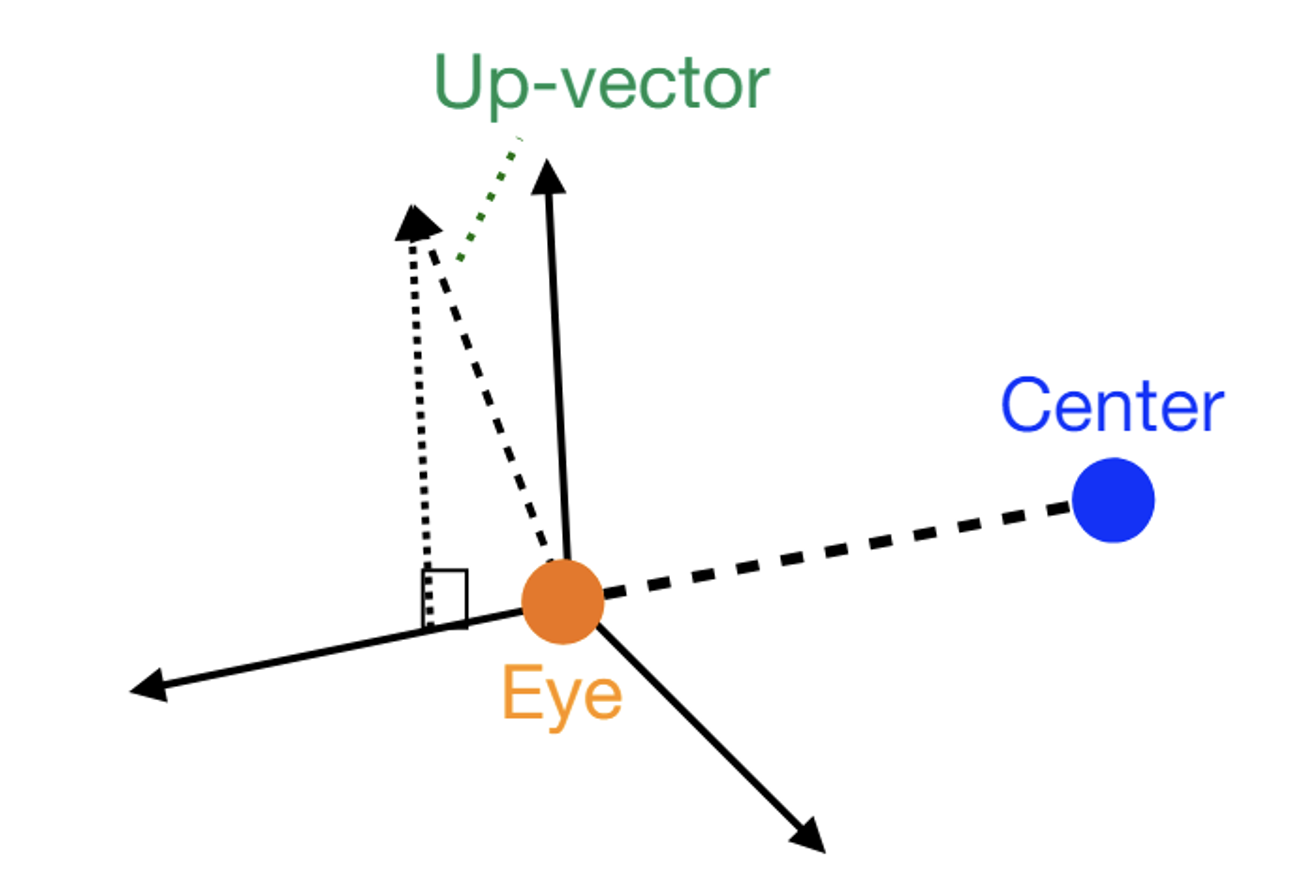
Eye(Camera Position): 카메라의 원점
Center(look-at point): 보는점
Up-Vector: 카메라의 윗부분이 어디를 향하는지
-
Z축 정의
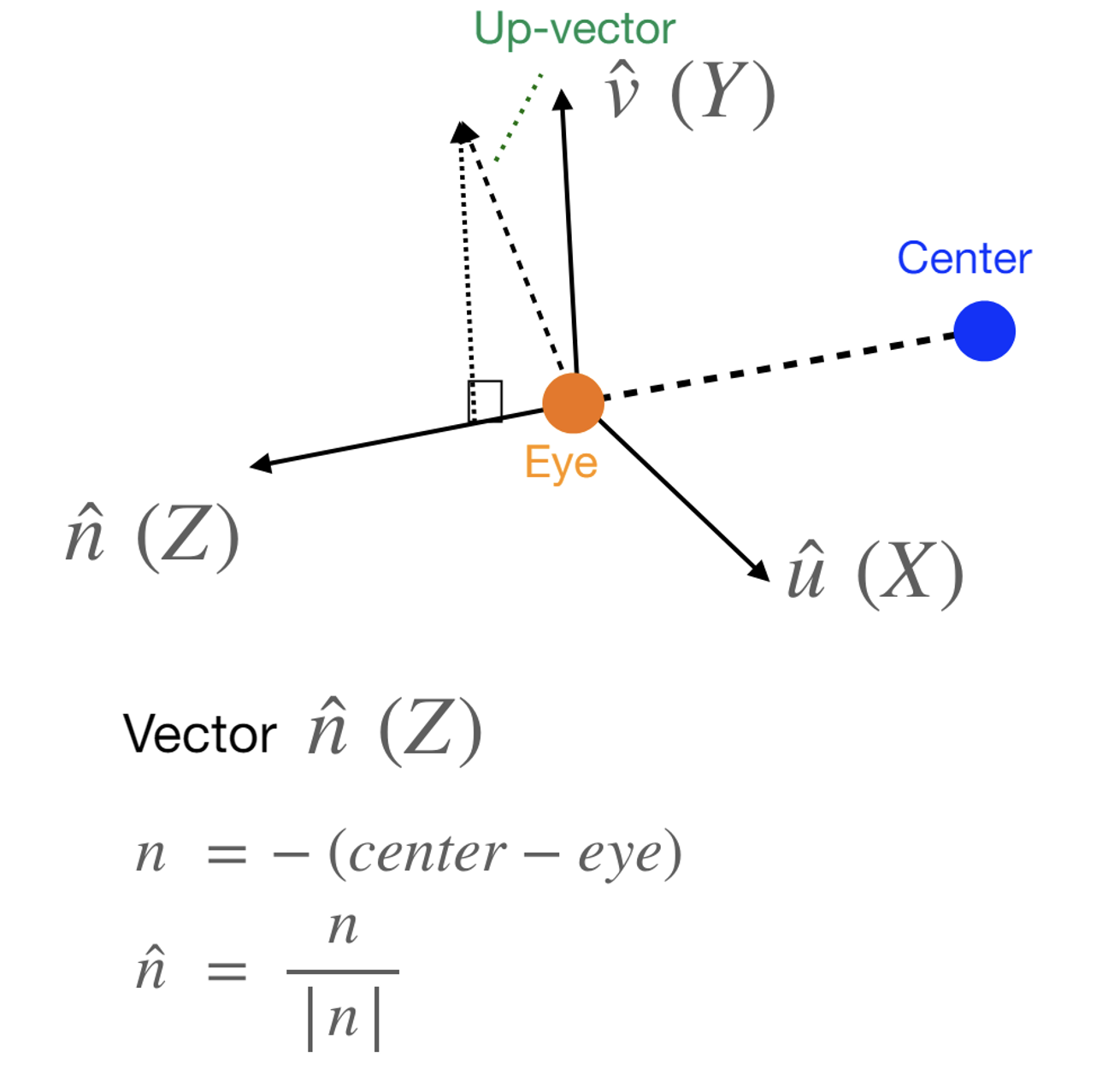
Center와 Eye를 이용해서 방향을 잡고 정규화
-> n = -(Center-Eye) <방향 설정> → n / InI <유닛 벡터> -
Y축 정의
up벡터를 자신을 z축에 정사영해준만큼 빼준 벡터 이후 정규화
-> v = up − (up ⋅ n)̂ n ̂ <빼준 벡터> → v / IvI <유닛 벡터> -
X축 정의
Z와 Y축의 Cross Product(외적) 결과

Camera -> Projection (Xpc) "Projection Matrix"

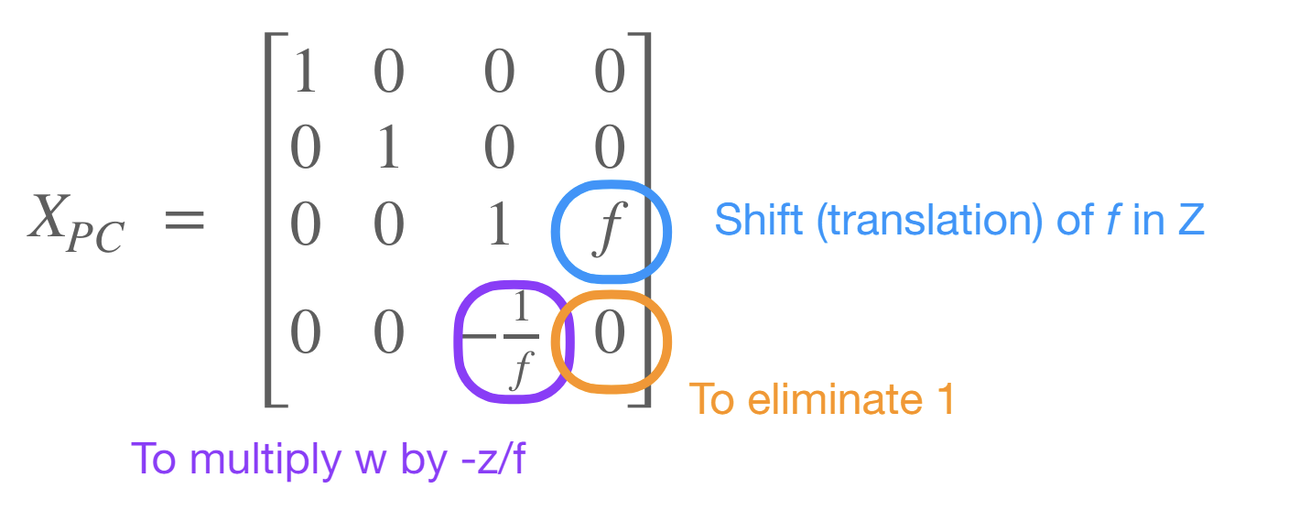
zp를 ac에대해서 나타내면
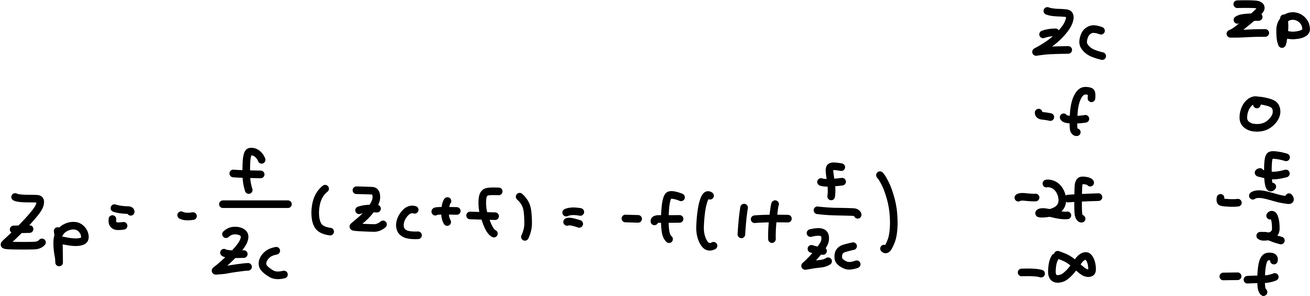
zp는 무조건 -f영역 내에 존재한다
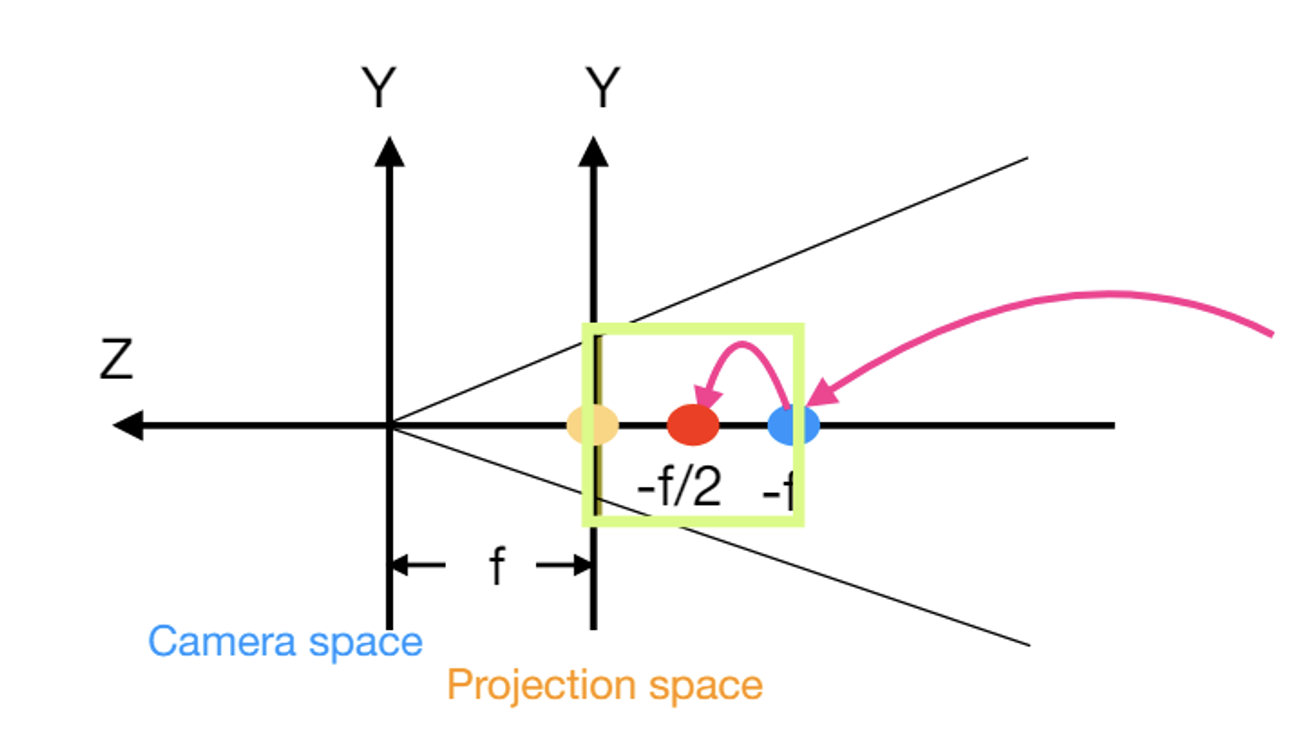
Projection -> Screen (Xsp) "Viewport Tranformation"
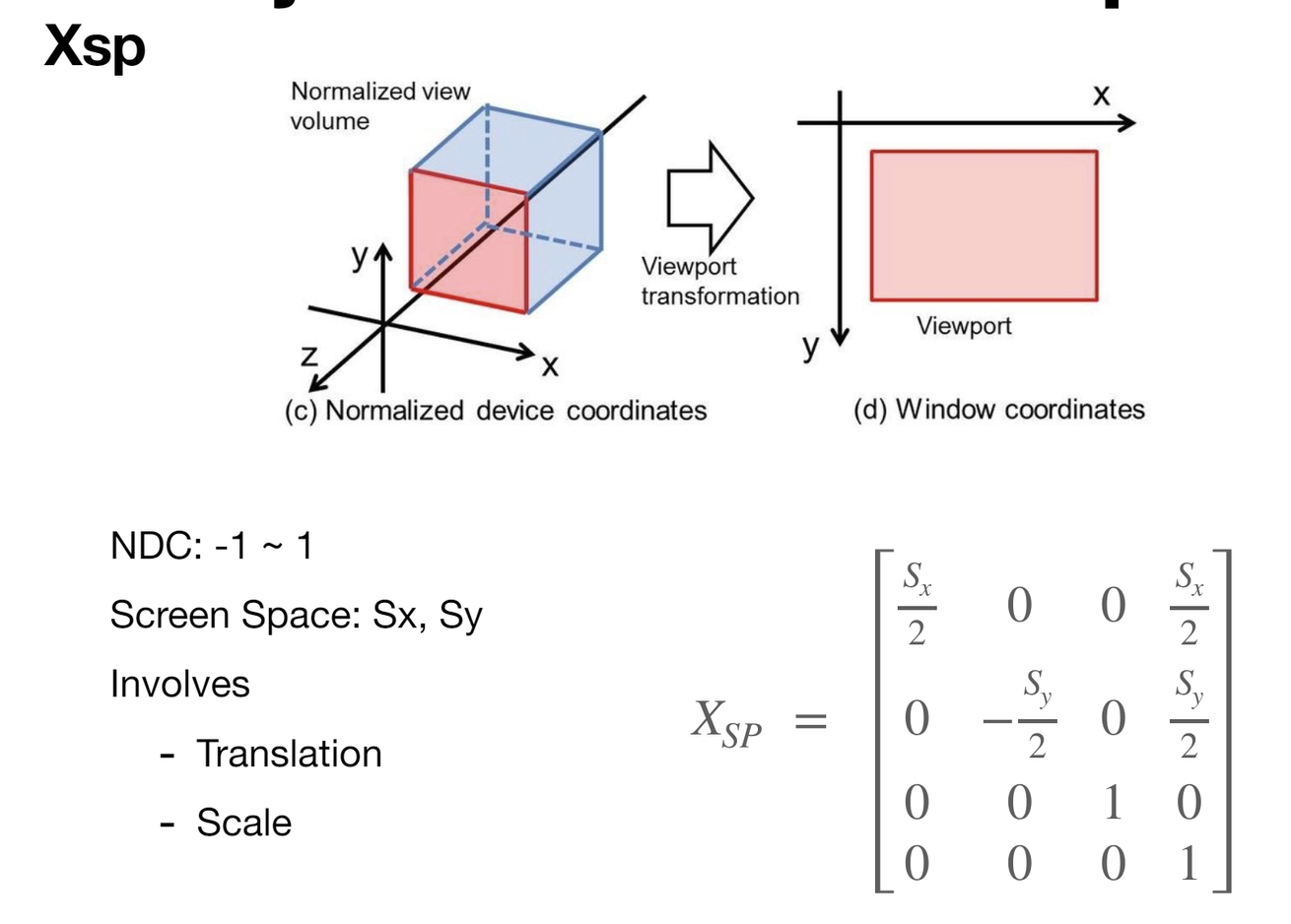
NDC: -1~1값으로 정규화
Screen 해상도: Sx, Sy
Scale: Sx/2 , -Sy/2는 스케일링하기 위해 사용
Translation: Sx/2 , Sy/2 좌표계의 원점 이동
Model -> Screen (Xsm) "총결산"
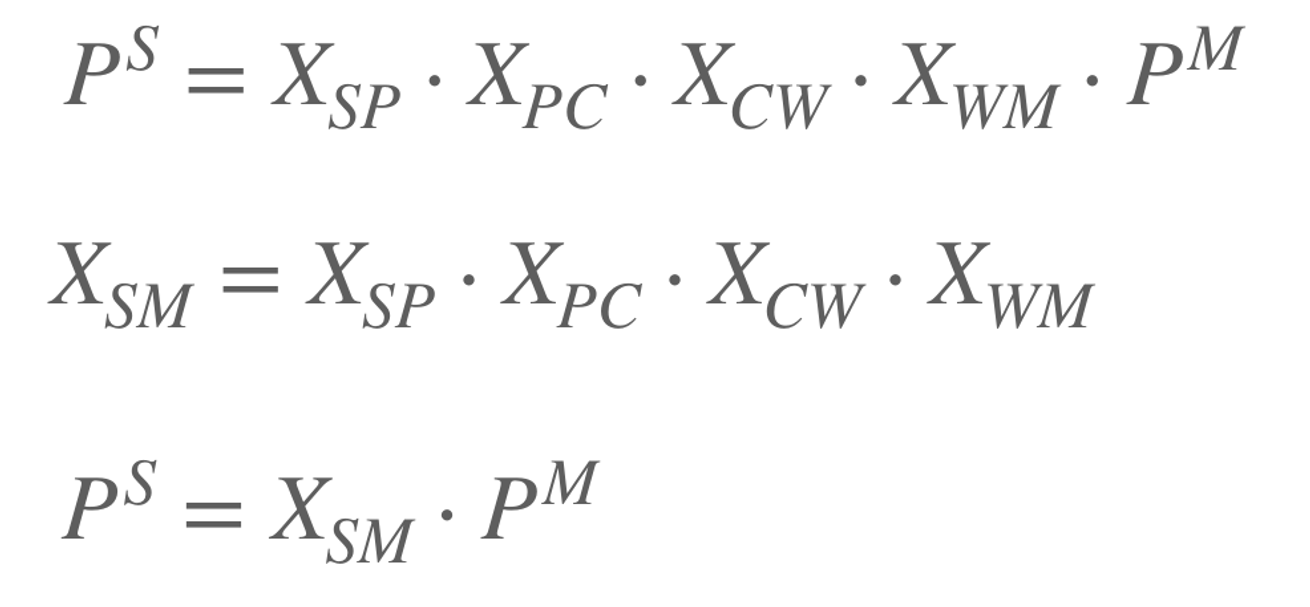
Rotation Details
Z축을 기준으로 θ만큼 회전하는 변환
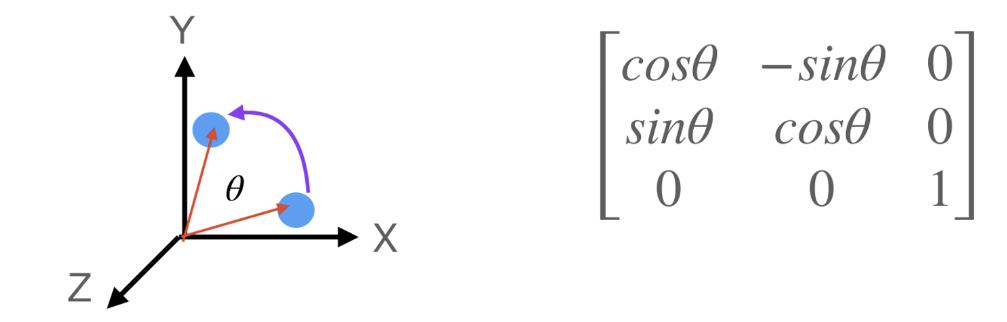
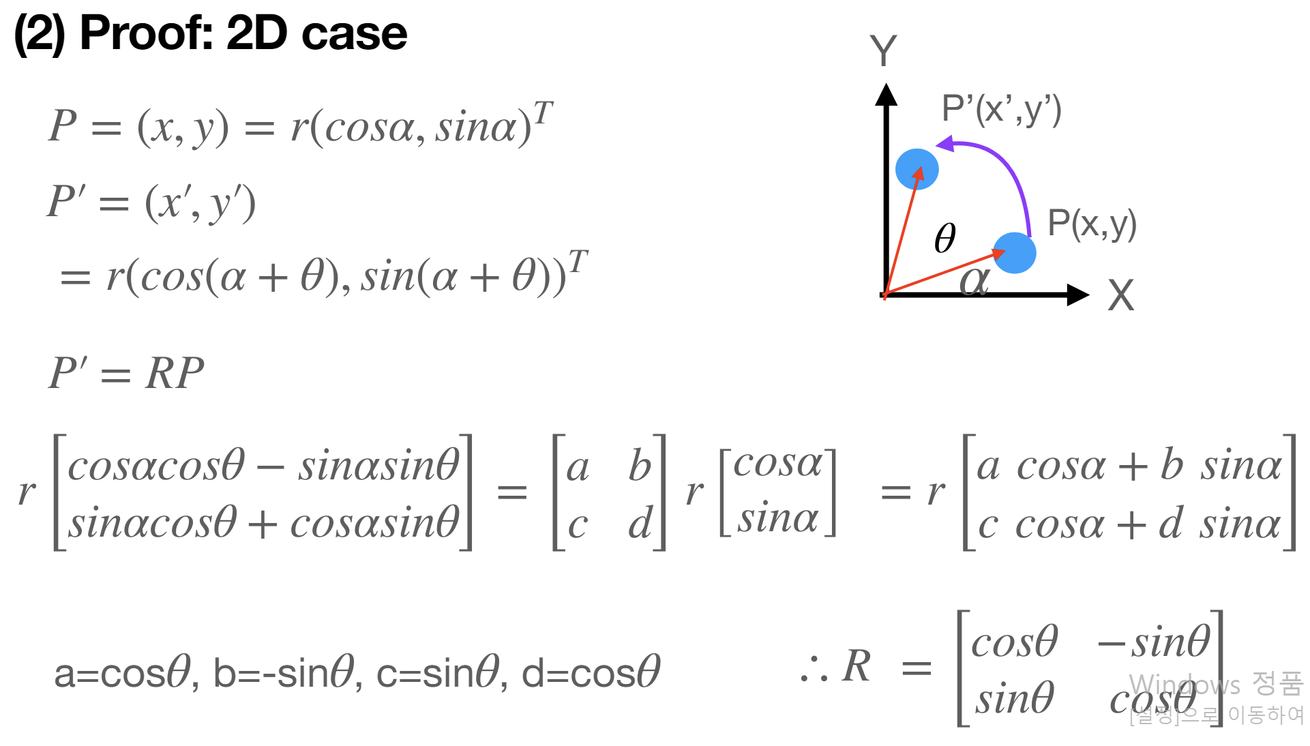
Proof
특징
1. Column / Row vectors are unit Vectors
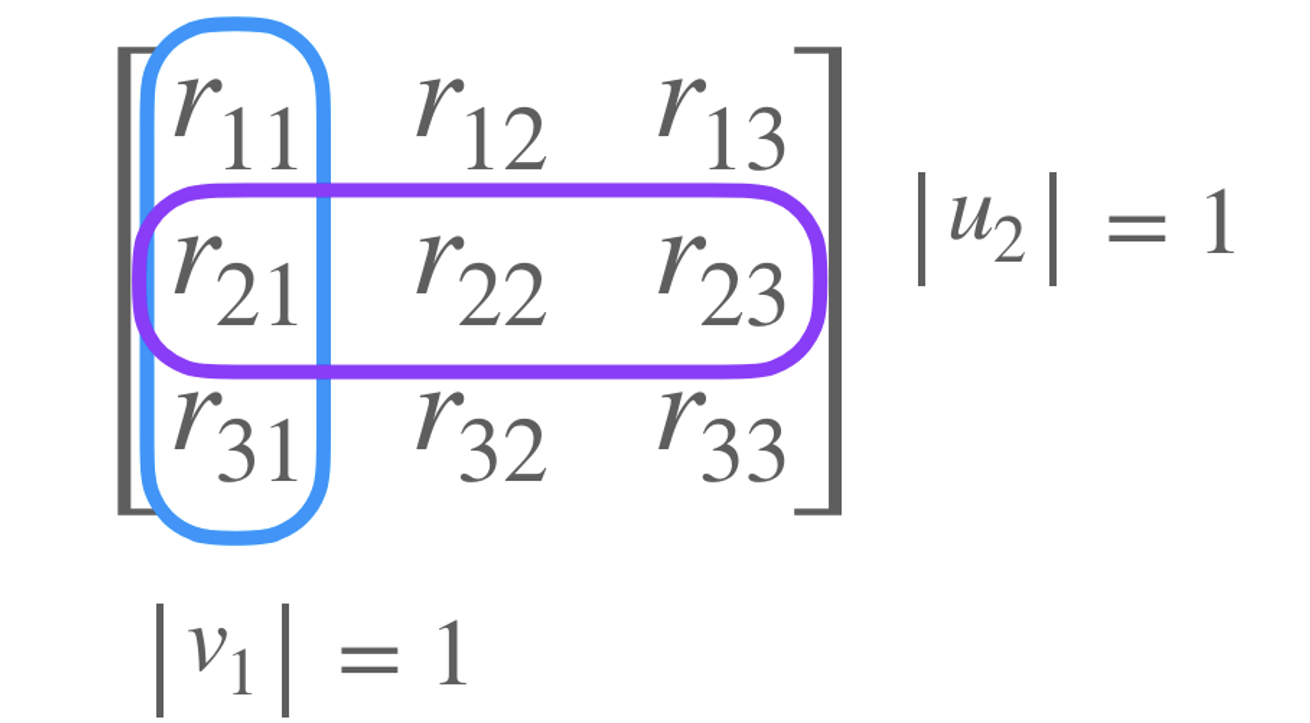
-
Colum / Row vectors are mutually orthogonal(직각)
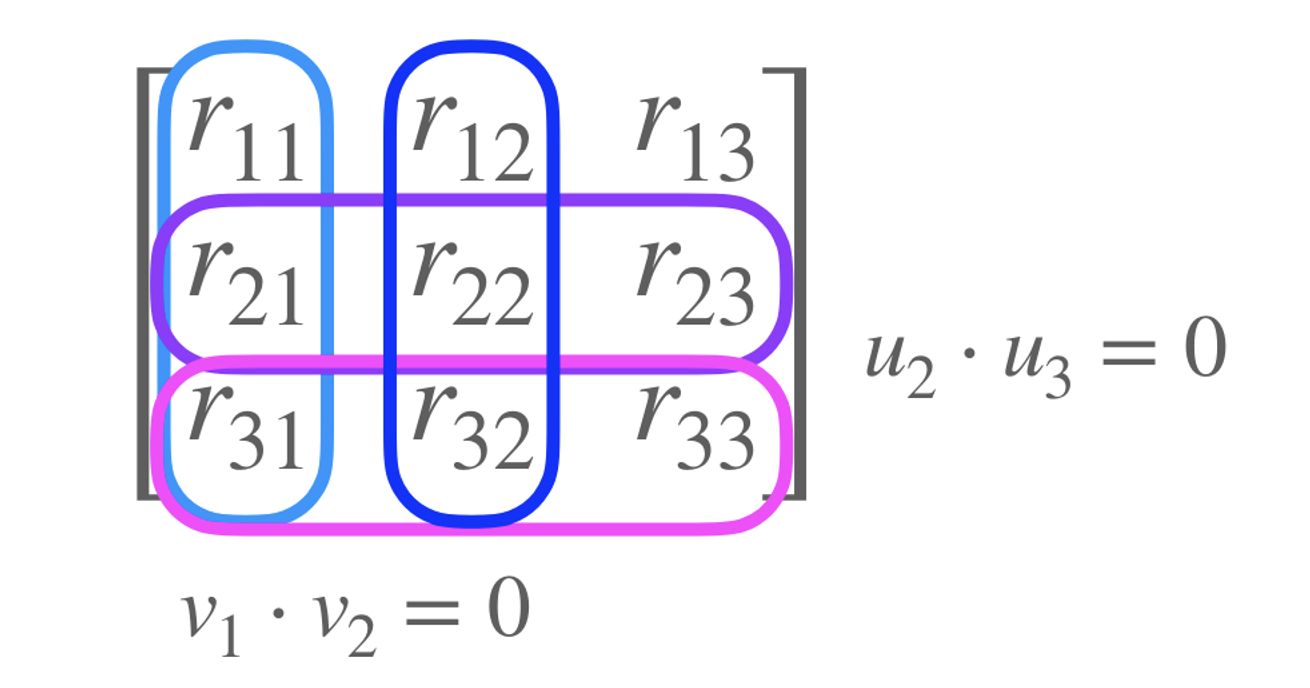
-
Inverse = Transpose
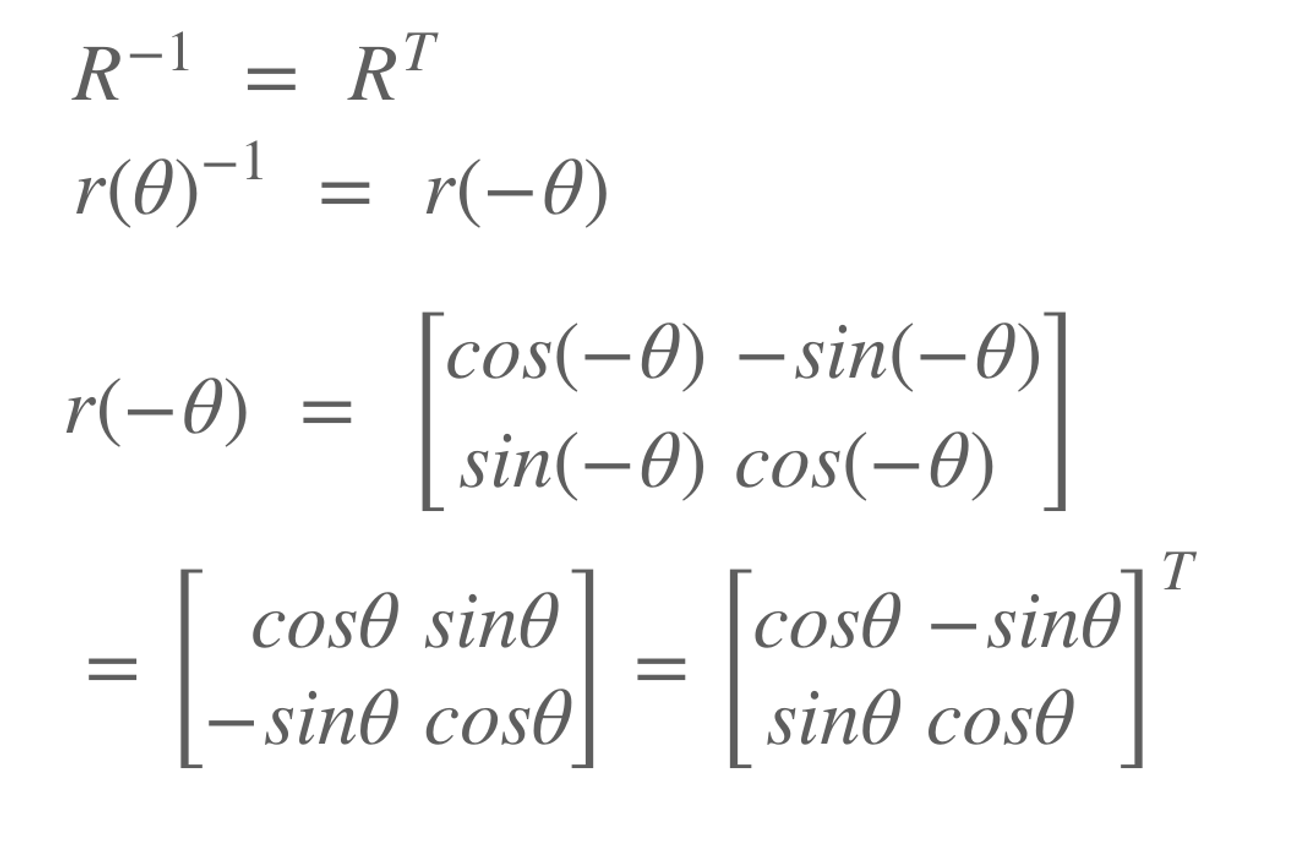
Rotation 방법
Euler Angles(오일러각)
세 가지 각도(α, β, γ)를 사용하는 방식 → 삼각함수(sin, cos)이용 "Non-linear"
Rotation Matrix
"linear"
Quartanion
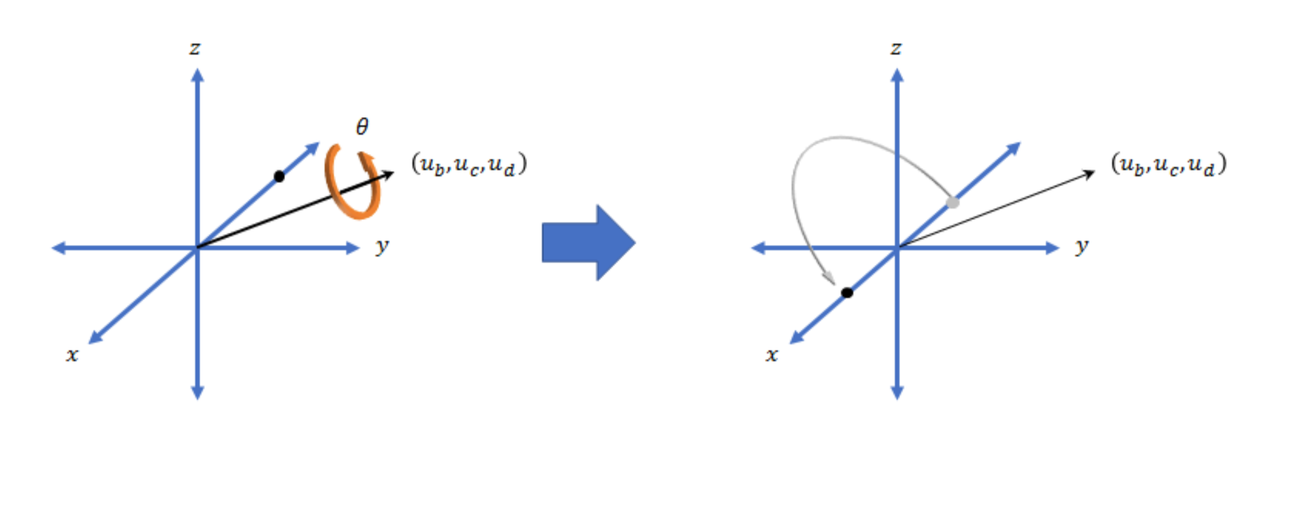
Vector (i,j,k) + angle "Non-linear"
요약

마무리
해당 내용은 대학 강의록 및 구글링을 통해 정리한 내용이므로 오류가 있을 수 있습니다.
