Rasterization
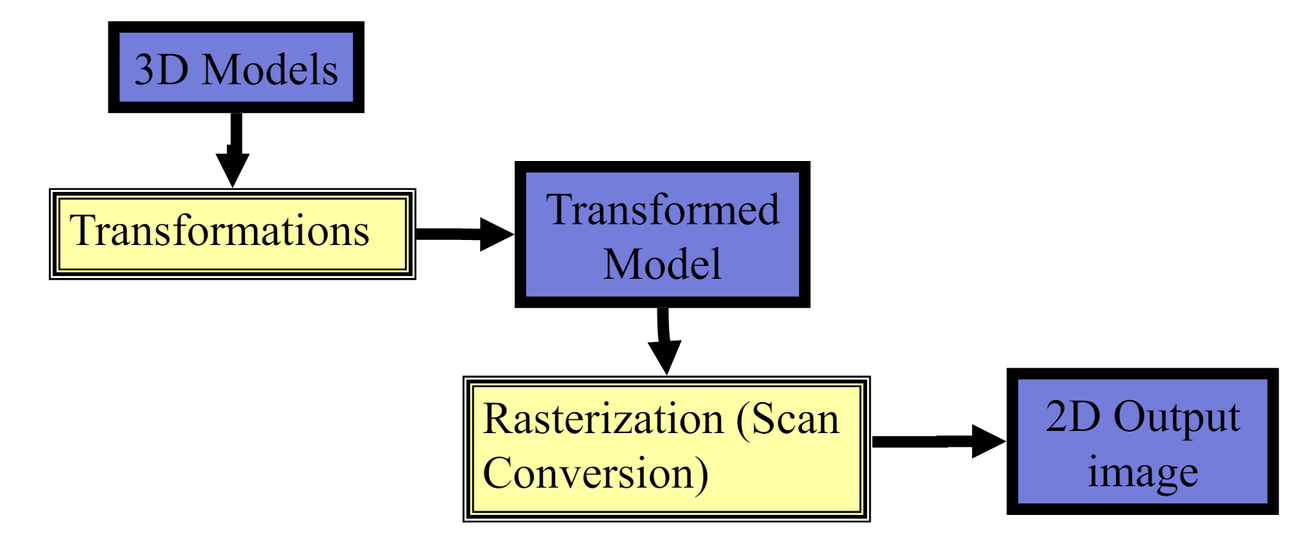
변환된 3D 모델을 실제로 화면에 표시하기 위해 픽셀로 변환하는 과정
계산과정
1. 좌표 변환을 사용하여 3D 정점의 픽셀 좌표 계산
2. 정점으로부터 선 또는 채워진 polygon 그리기
3. Scan Converting Lines -> 이상적인 선에 가깝게 픽셀을 계산하여 선을 그린다
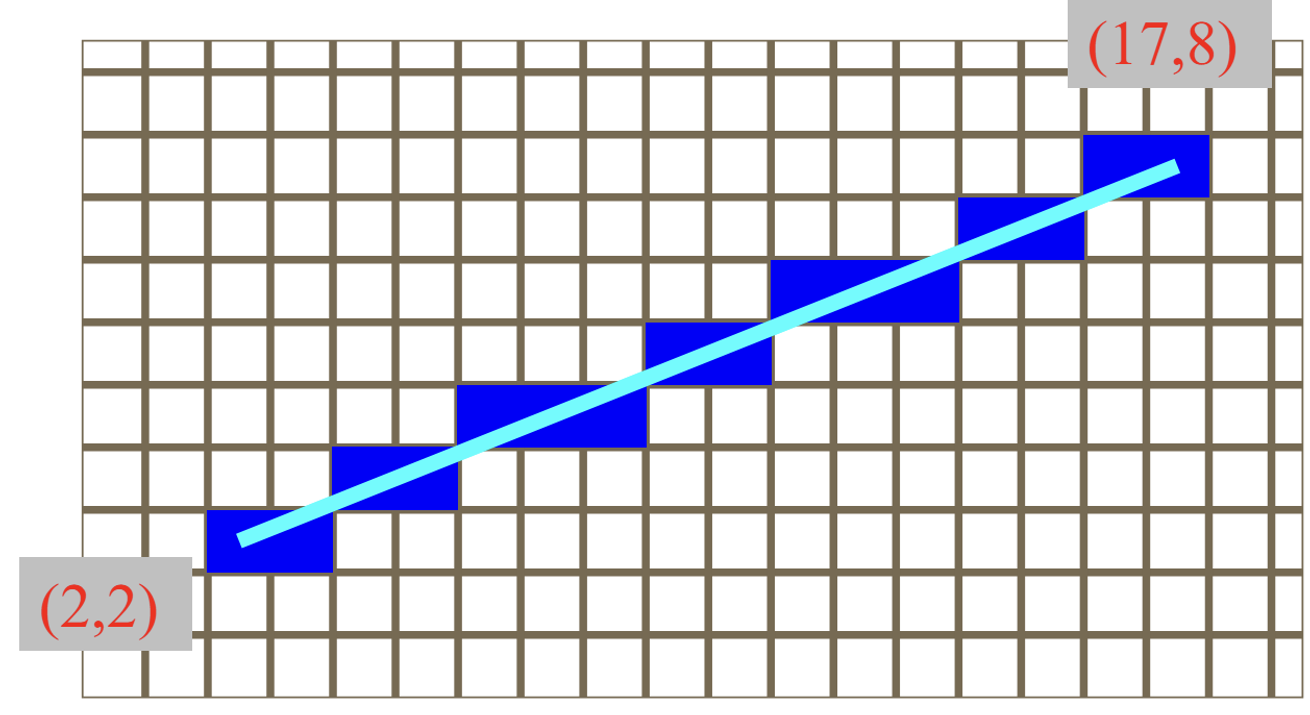
실제값: 진한 파랑색 픽셀 값들 -> 이상값: 하늘색 선
이상적인 선
- 연속적
- 균일한 두께와 밝기
- 실제 픽셀과 최대한 근접한 픽셀을 선택하여 그린다
- 적은 계산량으로 빠르게
Pseudo Code
void drawLine (int x0, int y0, int x1, int y1)
{
double dx = x1 – x0, dy = y1 – y0 ;
double m = dy / dx ; // m: 기울기(절댓값이 1보다 클 경우 x와 y의 역할 바꾼다)
int x ;
double y ;
for (x = x0, y = y0 ; x <= x1 ; x++) {
writePixel (x, round(y), color(x,y)) ; // round()사용으로 Compute Time 증가
y += m ; // y와 m이 실수여서 Compute Time 증가
}
}Visible Surface Determination
3D 장면을 렌더링할 때 어떤 표면이 시야에 들어오고 어떤 표면이 다른 물체에 의해 가려지는지를 결정하는 과정
Z-buffer algorithm
각 픽셀애 대해 Depth(깊이) 값을 저장하여 더 가까운 객체가 더 먼 객체를 덮어쓰도록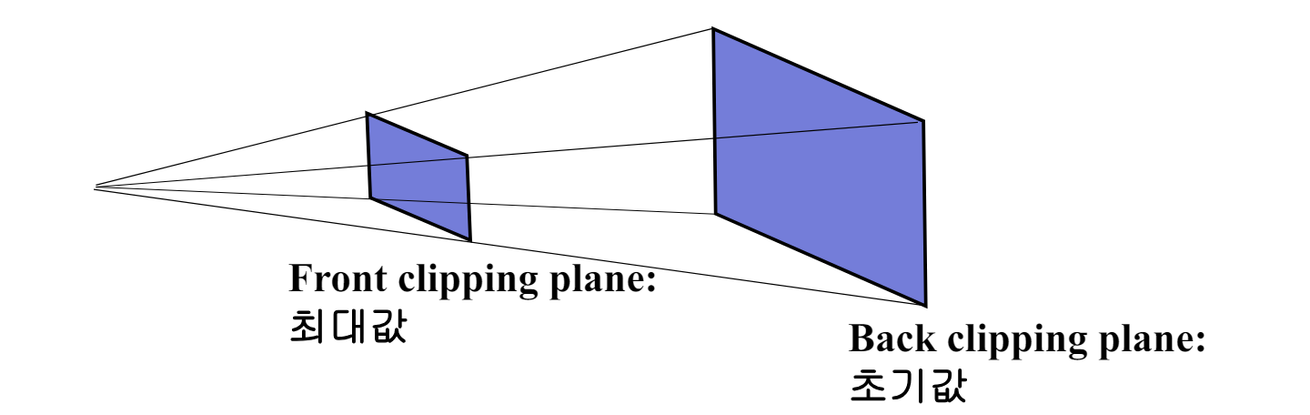
계산 과정
1. 3D 모델 좌표를 NDC(정규화)값으로 변환
2. 초기화: 모든 픽셀의 Z-buffer 값을 무한대로 설정
3. 각 픽셀에 대해 렌더링되는 객체의 깊이 값을 Z-buffer 값과 비교
4. 깊이가 더 작으면(더 가까우면) Z-buffer 업데이트하고 해당 픽셀을 화면에 그린다
void ZBufferAlgorithm()
{
int x, y ;
// 1. 초기화 단계: 화면의 모든 픽셀에 대해 Z-buffer와 색상을 초기화
for each pixel (x, y) on Screen
z_buffer (x, y) = INIT_Z ; // Z-buffer를 초기값으로 설정(INIT_Z는 일반적으로 매우 큰 값)
set_pixel(x, y, INIT_COLOR); // 색상을 초기값으로 설정(INIT_COLOR는 배경 또는 초기화 색상)
// 2. 각 폴리곤을 처리하는 단계: 각 폴리곤에 대해 화면의 모든 픽셀을 검사
for each polygon P
for each pixel (x, y) in P
compute z_depth at x, y // 해당 픽셀 (x, y)에서의 깊이 값을 계산
if z_depth > z_buffer (x, y)
then set_pixel (x, y, color) // 해당 픽셀의 색상을 폴리곤 P의 색상으로 설정
z_buffer (x, y) = z_depth // Z-buffer 값을 현재 깊이 값으로 갱신
}Z값 계산 방법1: 평면 방정식(Planer Equation)이용
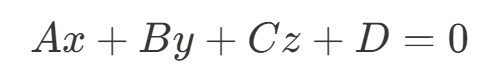
1. 평면 방정식을 Z에 대해서 나타낸다
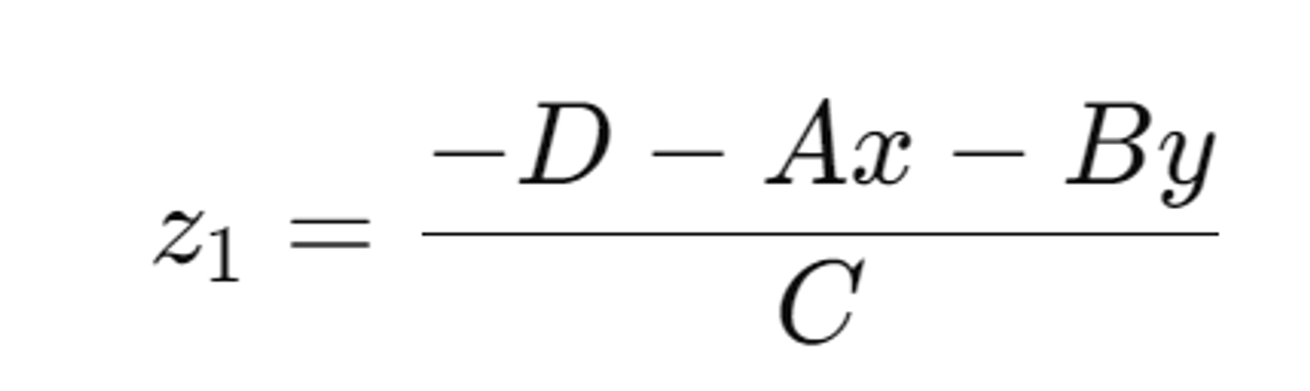
- (x,y)대신 (x+1,y)를 대입 -> z2를 z1에서 한단위 증가(x값의 변화에 대해 일정하게 증가)
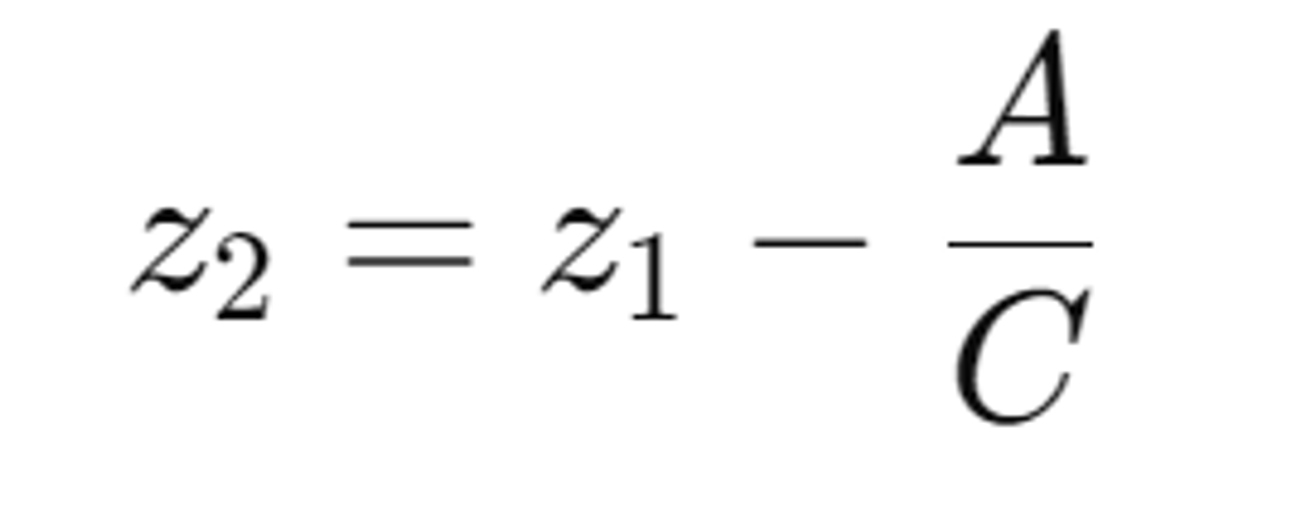
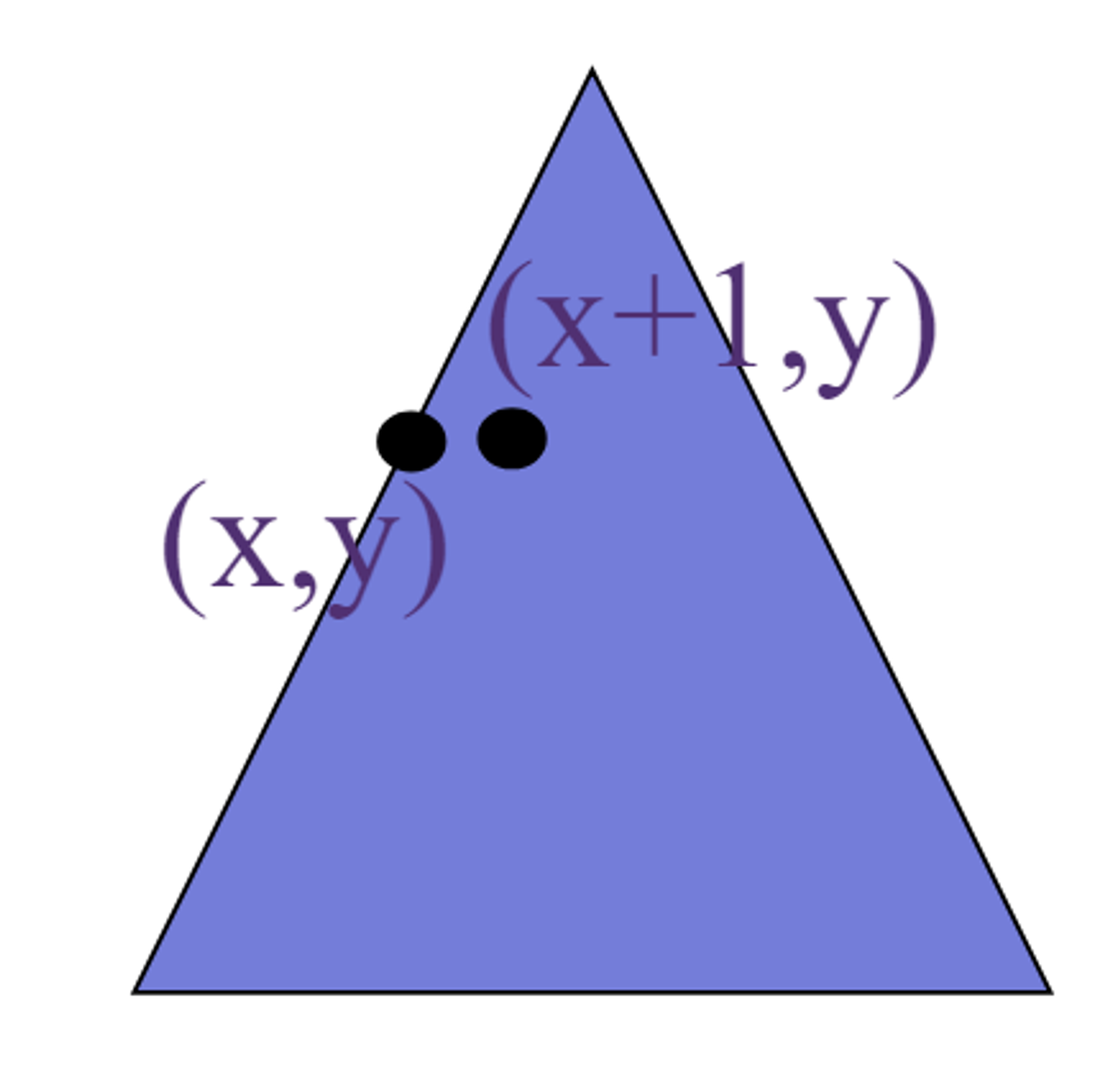
z값 계산 방법2: Ineterpolation
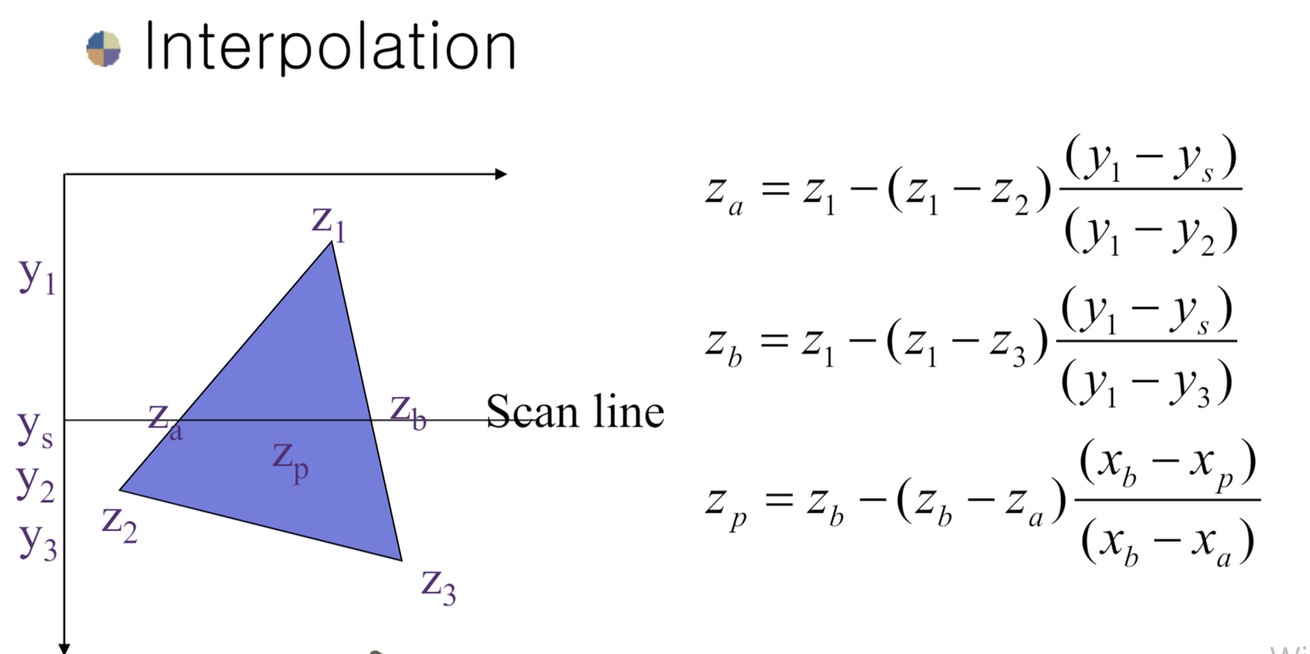
Z-buffer algorithm 장점: 빠르다
단점: 추가적인 메모리와 시간
Brute Force Method
입력으로 받는 다각형이 볼록(convex)하다고 가정 -> 비효율적(연산량이 많고 복잡하다)
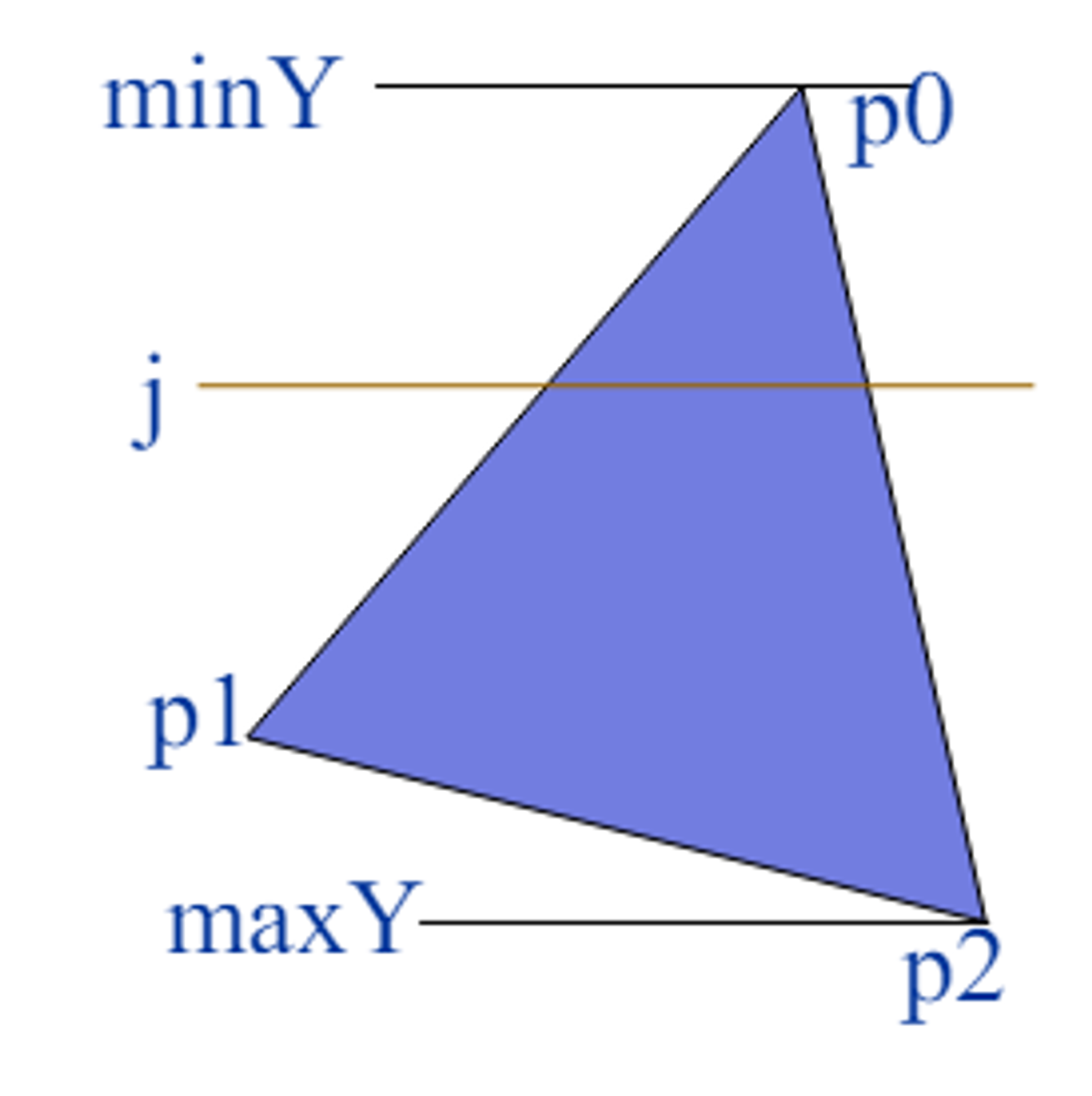
작업 순서
1. 다각형의 각 정점을 순회하여 minY와 maxY찾기
2. minY부터 maxY까지의 범위내에서 각 스캔라인(y=j)에 대해 반복
각 스캔라인 마다 다각형의 각 모서리 (po,p1)를 검사하여 교차점을 찾기
3. p0와 p1사이의 선형 보간을 사용하여 t값을 만족하는 p찾기
p = p0 + t(p1 - p0)이며 y=j 만족 -> t값을 통해 xLeft와 xRight 찾기
4. xLeft부터 xRight까지의 x좌표에 대해 반복
각 x좌표에서 Z값과 색상을 계산
illumination
물체의 색깔값을 계산하는 알고리즘 혹은 모델
Ambient(주변) Light
장면 전체에 고르게 퍼져서 모든 물체에 균일하게 적용되는 기본적인 배경 조명
특징
- 균일한 조명: 동일한 양의 빛때문에 그림자가 생기지 않는다
- 간단한 계산
- Diffuse, non-directional source of light
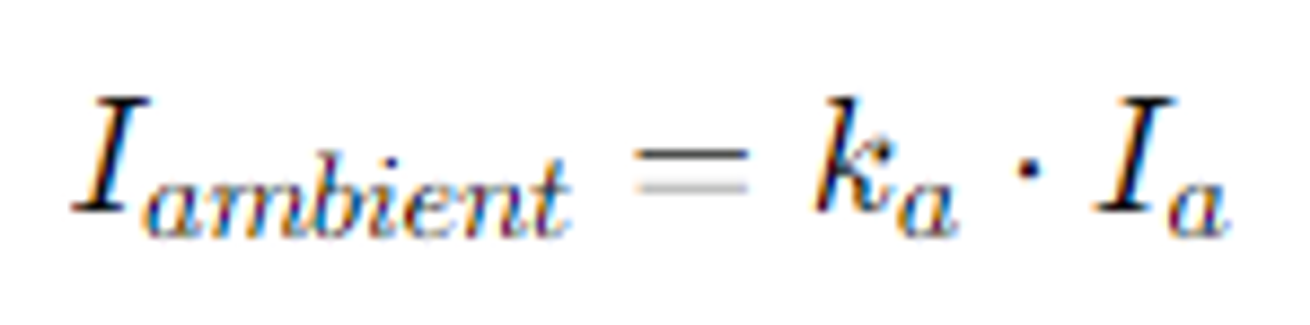
Iambinet: Ambient Light의 세기<특정 물체가 받는 최종적인 조명 세기> // ka: 물체의 반사 계수 // Ia: Ambient Light의 세기<기본적인 조명 세기>
Diffuse(퍼지는) Light
표면에 고르게 퍼져 특정 방향에서 오는 빛을 난반사하여 물체의 색상과 형태를 부드럽게 드러내는 조명
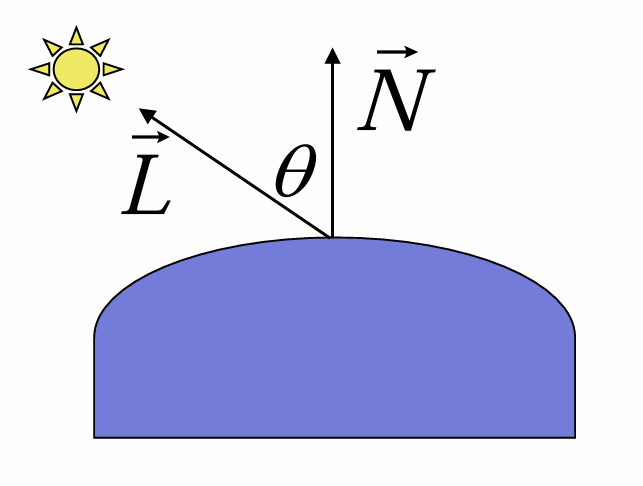
특징
- 표면의 각도에 따른 밝기 변화 (Max: 수직(N,L방향이 같을 때), 각도가 커질수록 어둡다)
- 그림자와 하이라이트를 표현하는 사실적인 조명
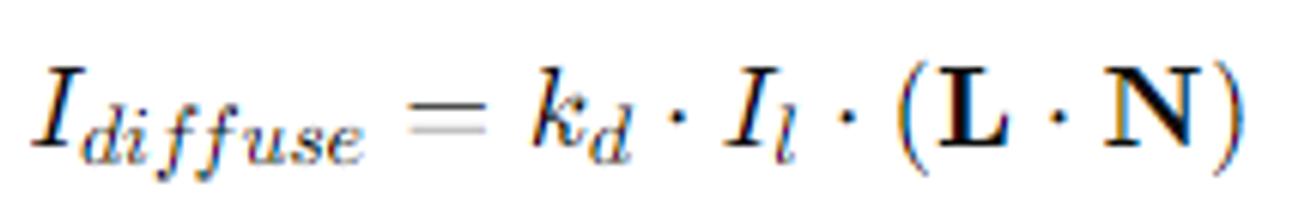
Idiffuse: Diffuse Light의 세기 // kd: 물체의 반사 계수 // Il: 광원의 세기
L: 광원으로부터 오는 빛의 방향 벡터 // N: 객체 표면의 법선벡터
Directional Light Source
특정 방향에서 평행하게 입사하여 일정한 방향으로 빛을 비추는 광원
광원은 매우 먼 곳에서 빛이 온다고 가정하여 빛의 방향이 일정하게 유지
-> L 값(광원으로부터 오는 빛의 방향 벡터)이 상수가 된다!
Light Attenuation(감쇠) Model
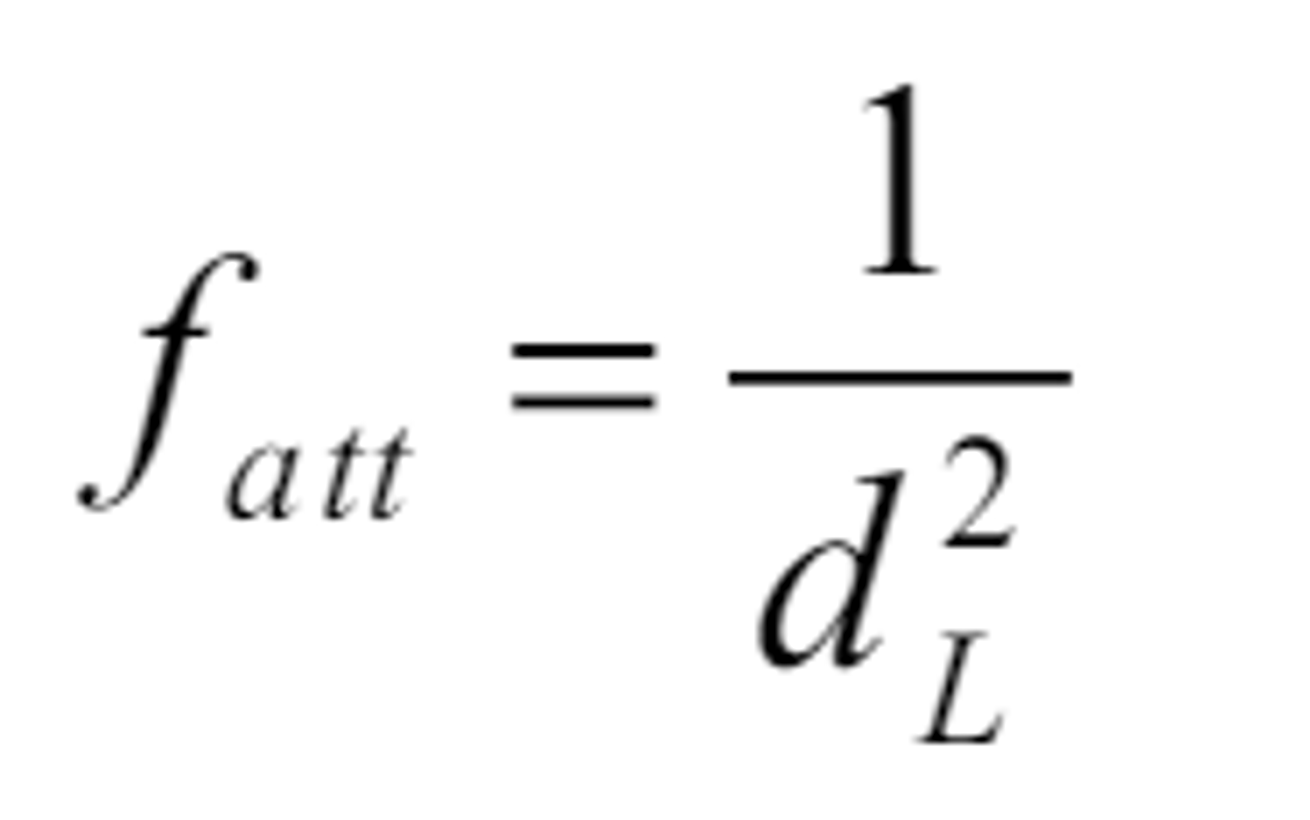
빛이 멀어질수록 강도가 약해진다 -> 거리의 제곱에 비례해서 작아진다
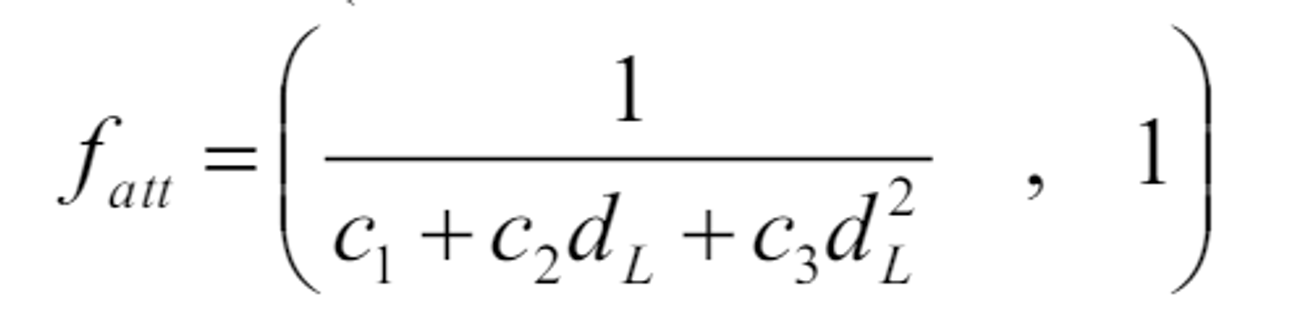
실제와 더 유사한 식(c1,c2,c3 -> 계수)
Colored Lights and Surfaces
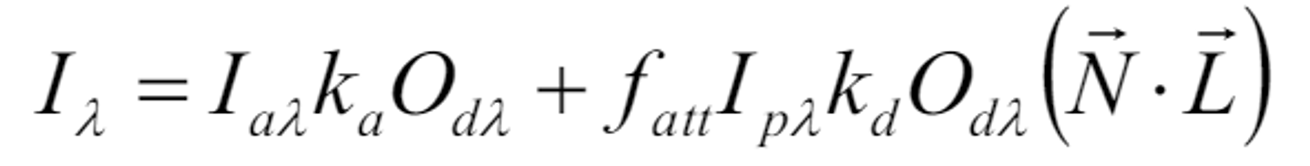
𝐼𝜆: 일반적인 색상 채널(λ)에서의 최종 조명 강도
"Ambient Light"
Iaλ: 주변광 (ambient light)의 일반 채널에서의 강도
ka: 주변광 반사 계수 (ambient reflectivity)
Odλ: 객체의 확산 반사 색상 구성 요소 (diffuse color components)
"Diffuse Light"
fatt: 빛 감쇠 계수 (attenuation factor)
Ipλ: 광원의 일반 채널에서의 강도
kd: 확산 반사 계수 (diffuse reflectivity)
N: 표면의 법선 벡터 (surface normal vector)
L: 광원 방향 벡터 (light direction vector)
Specular(거울같은) Light
광원이 반사되는 표면에서 특정 방향으로 강하게 반사되어 밝은 하이라이트를 생성하는 조명
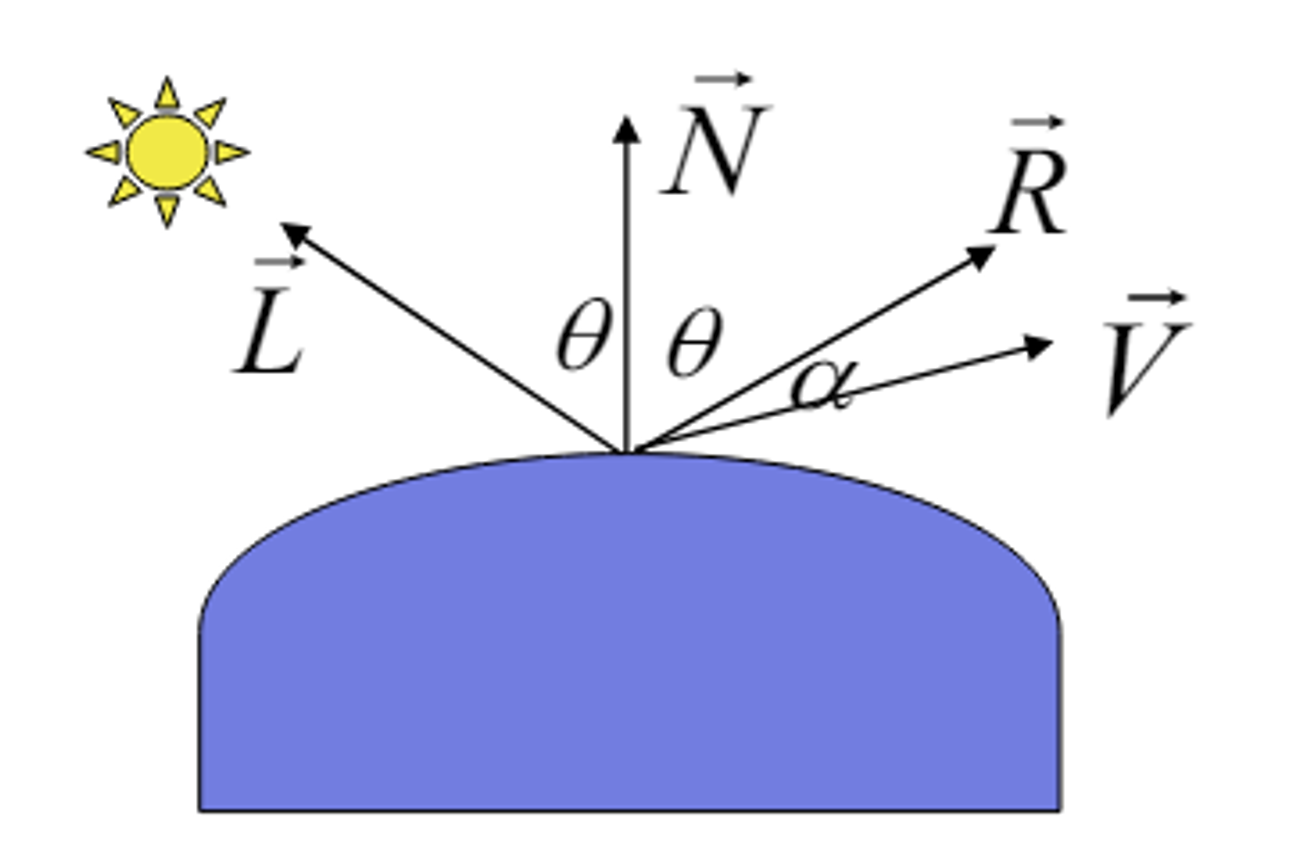
- 빛나는 표면에서 관찰된다
- 반사광때문에 하이라이트가 관찰된다
- 거울같은 완전 Shiny한 물체에서는 a값이 0이되어 반사로 R만된다
Phong illumination Model
Specular reflectance 최대값: a가 0일때(mirror) -> a가 커질수록 감소
cos^n(a): 하이라이트가 어떻게 변하는지에대한 근사치
n: 물체의 specular-reflection exponent -> n이 클수록 매끄럽고, 하이라이트가 작고 뚜렷
ks: 표면의 반사광 계수
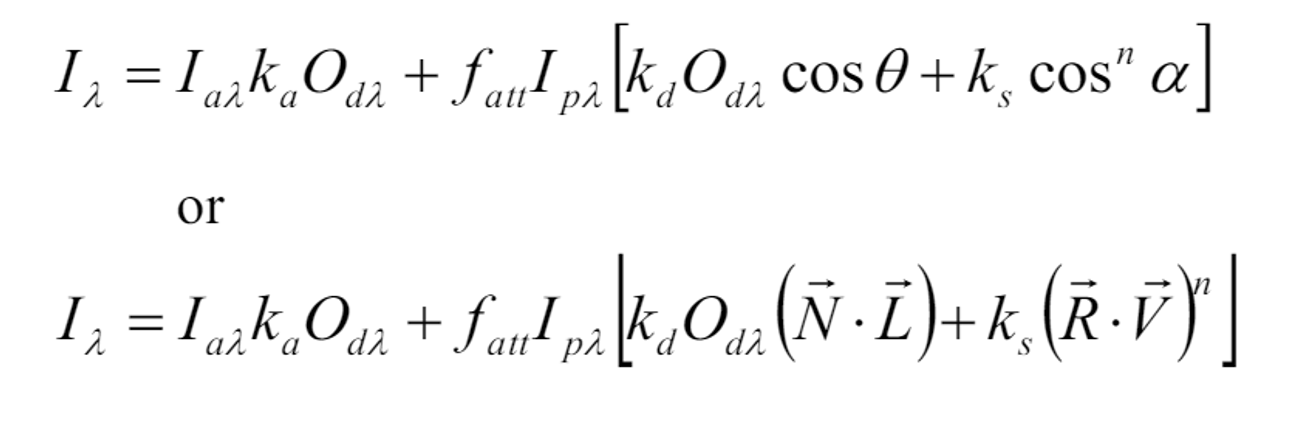
요약

마무리
해당 내용은 대학 강의록 및 구글링을 통해 정리한 내용이므로 오류가 있을 수 있습니다.
