간단한 DDPM설명: https://velog.io/@guts4/Basic-Generative-Model-DDPM

DDPM 수식 설명 및 완벽 분석: https://velog.io/@guts4/DDPM-%EC%88%98%EC%8B%9D-%EB%B0%8F-%EB%85%BC%EB%AC%B8-%EC%99%84%EB%B2%BD-%EB%B6%84%EC%84%9D

DDIM은 DDPM의 좋은 성능과 mode converage 능력은 그대로 가져오고, 시간을 단축하기 위해서 생성된 모델입니다. 어떻게 시간을 단축할 수 있는지를 중점적으로 논문을 읽으면 도움이 되실겁니다.

VARIATIONAL INFERENCE FOR NON-MARKOVIAN FORWARD PROCESS

왼쪽 그림은 DDPM의 Markovian 과정을 나타낸 것이고, 오른쪽은 DDIM에서 제시한 non-Markovian 과정을 나타낸 것입니다. Markovian 과정은 이전 step의 영향만을 받는다는 점인데요, 그래서 왼쪽 그림에서 $x_2$는 $x_1$의 영향만을 받는다고 화살표로 표시되어있지만, 오른쪽 non-Markovian에서는 화살표가 직전 step이 아닌 $x_0$의 영향도 받는 것을 확인할 수 있습니다. 어떻게 이러한 과정이 가능한지 아래에서 자세히 설명해드리겠습니다.

NON-MARKOVIAN FORWARD PROCESSES

완전히 초보인 제가 본 시점을 기준으로 설명해드리도록 하겠습니다.

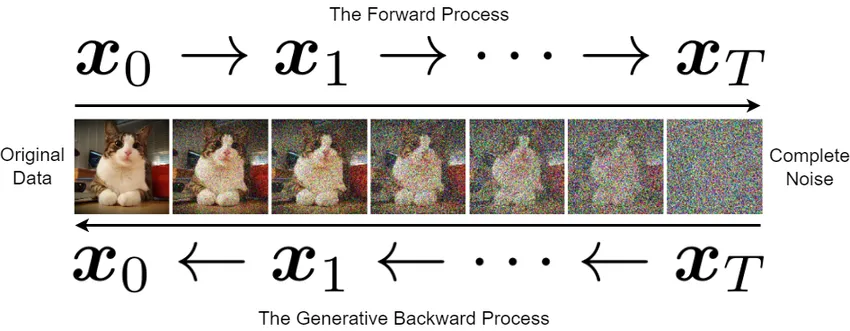
DDPM 에서는 forward process가 한 step씩 진행되도록 학습을 진행합니다. 즉 노이즈를 조금씩 추가하면서 가우시안 분포로 바꾸고, 이렇게 학습했기 때문에 reverse process도 마찬가지로 한 step씩 노이즈를 제거하면서 원본 이미지를 복원했습니다.

DDIM은 이러한 과정이 너무 오래걸리기 때문에 reverse process를 한단계씩 진행하는 것이아닌 몇 step은 건너뛰는 식으로 진행하길 원했습니다. 이렇게 reverse process를 정의했기 때문에 forward process도 변경해야합니다.

한단계씩 진행하는 이유는 어떤걸까요? 바로 Markovian process때문입니다. 이를 non-Markovian chain으로 바꾸는게 핵심입니다.

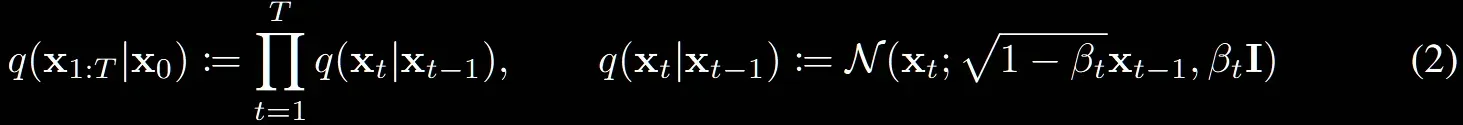
위의 수식은 DDPM의 forward process입니다. $q(x_t|x_{t-1})$에서 보이는 것처럼 이전시점에만 영향을 받는 상태입니다. 그러면 이전 시점에만 영향을 받는게 아니라 원본이미지로부터의 영향도 존재한다고하면 non-Markovian process 형태로 정의할 수 있습니다.

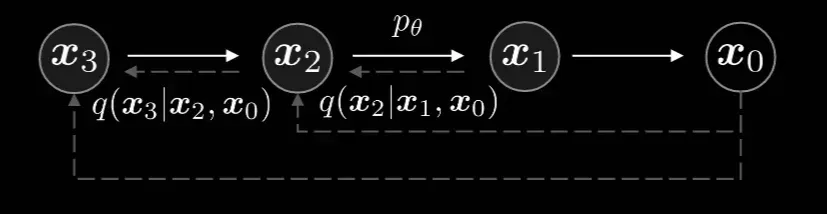
이제 다시 DDIM의 그림을 살펴보겠습니다. 수식이 $q(x_t|x_{t-1},x_0)$즉 이전시점과 처음시점 모두에 영향을 받는것을 알 수 있습니다.

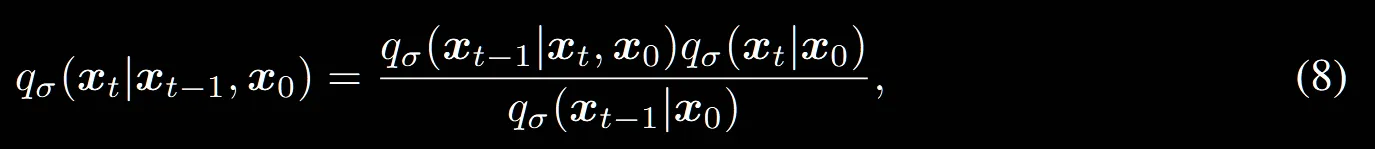
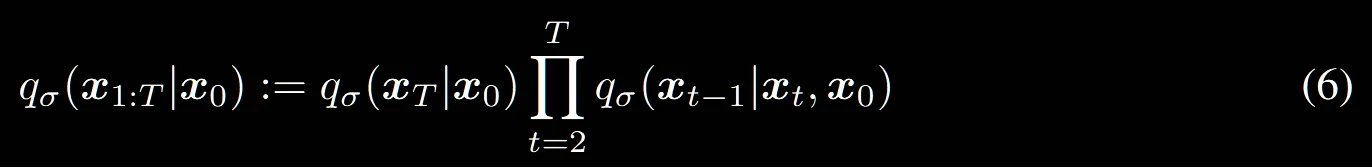
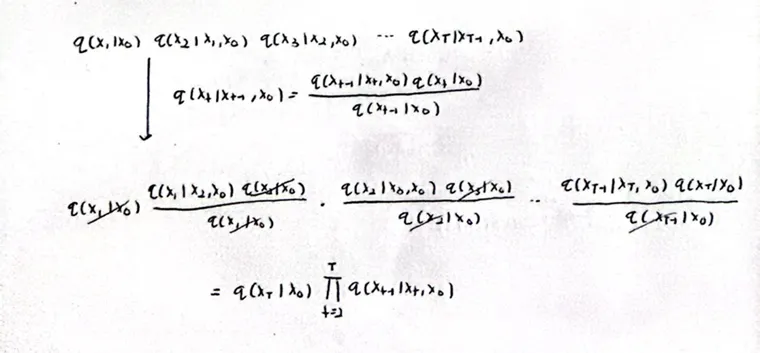
수식 $q(x_t|x_{t-1},x_0)$을 t=1~T까지 모두 전개하면 맨 위의 수식이됩니다. 이후 논문의 베이즈 정리 식(8)을 적용하면 최종적으로 수식(6)이 나오는 것을 알 수 있습니다.

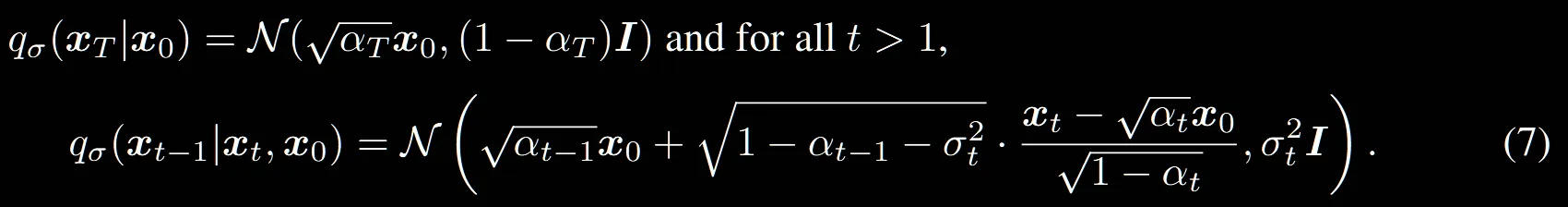
그리고 위의 수식에 대해서 평균과 분산에 대한 데이터의 분포를 나타내면 최종적으로 수식(7)이 나옵니다.

따라서 forward process는 더이상 Markovian이 아닌 것을 확인할 수 있습니다.

만약 분산($\sigma$)값이 고정되어있다면, forward process과정이 stochastic 해지지 않고 deterministic 해지는 것을 확인할 수 있습니다. 왜냐하면 분산이 클수록 데이터들이 평균으로부터 멀리 떨어져있다는 뜻이기 때문입니다.

GENERATIVE PROCESS AND UNIFIED VARIATIONAL INFERENCE OBJECTIVE

논문에서는 $x_t$로부터 노이즈를 제거한 $x_0$를 얻고 이를 이용해서 $x_{t-1}$을 구한다고했습니다.

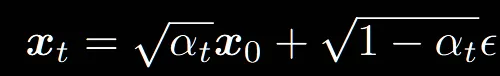
위의 수식에서 $\epsilon$을 $\epsilon_{\theta}^{(t)}(x_t)$으로 노이즈를 예측하는 네트워크로 변경하고, $x_0$에 대해서 정리하면 최종적으로 아래의 수식이 나옵니다.

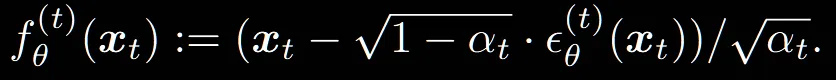
이렇게 $x_0$를 f에 대한 수식으로 바꾼 이유는 우리가 $x_0$에 대해서 알 수 없기 때문입니다.

이제 수식(7)에 $x_0$대신 f에대한 수식을 대입하면 최종적인 generative process가 위와 같이 정의됩니다.

결론적으로 위의 수식을 통해서 원래 존재하는 데이터의 분포와 예측한 데이터의 분포의 차이를 최소화하면서 $\theta$값이 최적화됩니다.

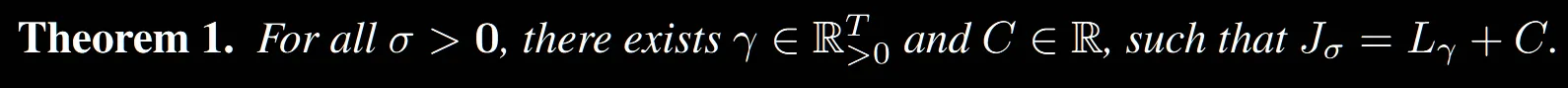
해당부분을 완벽하게 이해하지는 못해서 정확한 내용은 논문을 참고하면 좋을거 같습니다. 하지만 일단 이해한 내용을 설명해드리자면, 우리가 위에서 설명한 Jacobian식, 즉 원래 데이터 분포와 우리가 학습한 데이터의 분포의 차이를 최소화하는 학습 방법은 각 time step별로 학습한 U-Net모델의 Loss값과 동일하다는 것입니다.

U-Net 모델이 파라미터를 공유하고 있기는 하지만 입력으로 들어가는 time step(t)에 따라서 모델의 파라미터가 다르기때문에 이 이론이 성립된다고 설명됐습니다.

SAMPLING FROM GENERALIZED GENERATIVE PROCESSES

DENOISING DIFFUSION IMPLICIT MODELS

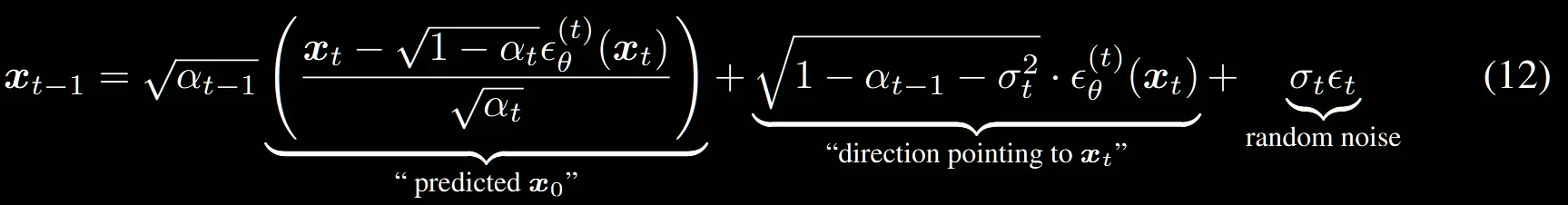
우리는 위에서 $x_t$의 분포로부터 $x_0$의 분포를 구하고 이를 기반으로 $x_{t-1}$의 분포를 구한다고 했습니다. 이를 한번에 $x_{t-1}$를 구한다고 했을 때 수식은 위와 같습니다.

위의 수식에서 맨마지막 부분에 있는 random noise의 값때문에 매번 다른 결과가 나오게 되는 것입니다. 만약에 매 step마다 $\sigma$의 값을 0으로 설정한다면 해당 과정은 deterministic하게 작동할 것입니다.

ACCELERATED GENERATION PROCESSES

이부분이 time step을 줄여서 최종적으로 diffusion의 시간을 줄이는 부분입니다.

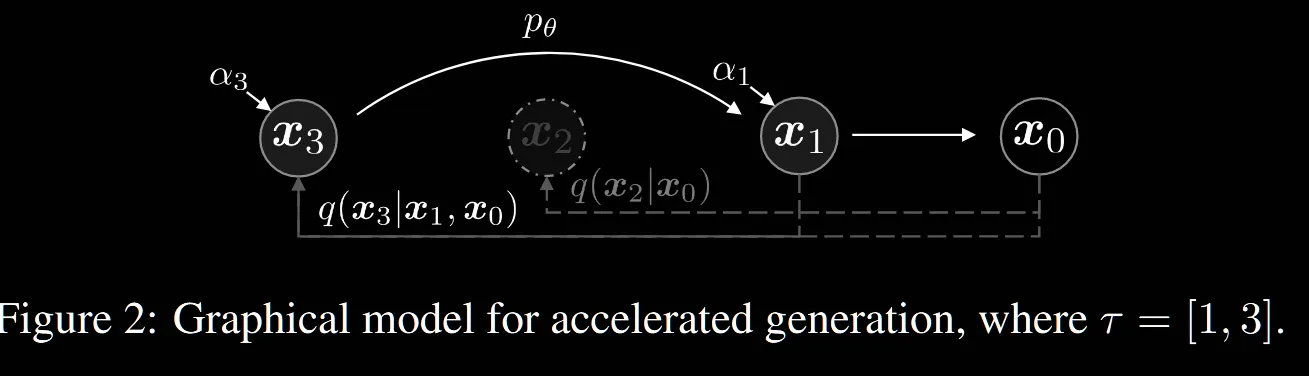
원래는 0~T까지 모든 경로를 진행해야 하지만, 이중에서 S개만을 뽑아낸 부분집합 τ에 대해서 진행하는 과정입니다.

$q(x_{\tau_i} \mid x_0) = \mathcal{N} \left( \sqrt{\alpha_{\tau_i}} x_0, (1 - \alpha_{\tau_i}) I \right)$의 수식을 만족하면서 sampling을 진행하게됩니다.

위의 수식은 1,3만 선택했을 때 진행되는 과정을 시각화 한 것입니다. $x_2$를 생략하면서 진행하는 것을 확인할 수 있습니다. 자세한 수식이 Appendix C.1에 있어서 해당 부분을 살펴보도록 하겠습니다.

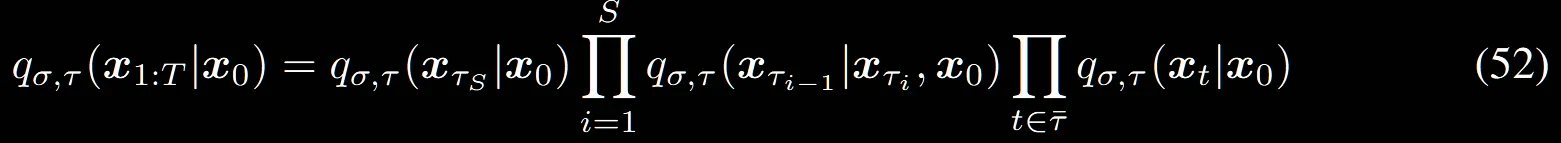
해당 식은 크게 2가지 부분으로 나눠질 수 있습니다. sub-sequence로 선택된 경우 왼쪽의 수식을, 아닌 경우는 오른쪽 수식입니다.

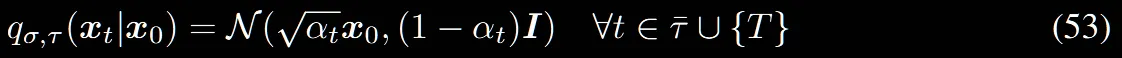
(52)의 수식에서 오른쪽 부분, sub-sequence로 선택되지 않은 단계에서의 정의입니다. 수식(4)와 비슷한 형태로 $x_0$에서부터 시작해서 일정한 계수를 통해 평균과 분산을 정의합니다.

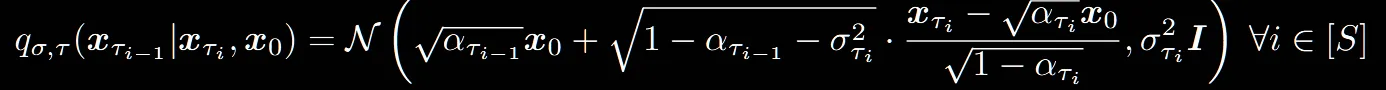
(52)번 수식에서 왼쪽 부분, sub-sequence로 선택된 단계에서의 정의입니다.

수식(7)과 동일하게 이전단계와, 초기값을 이용해서 분포를 구합니다.

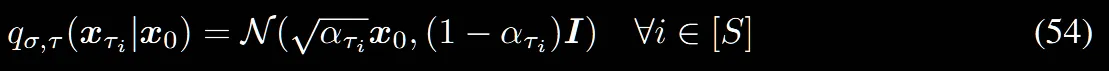
(54)번 수식과 동일한데 T가아닌 S라고 보시면됩니다.

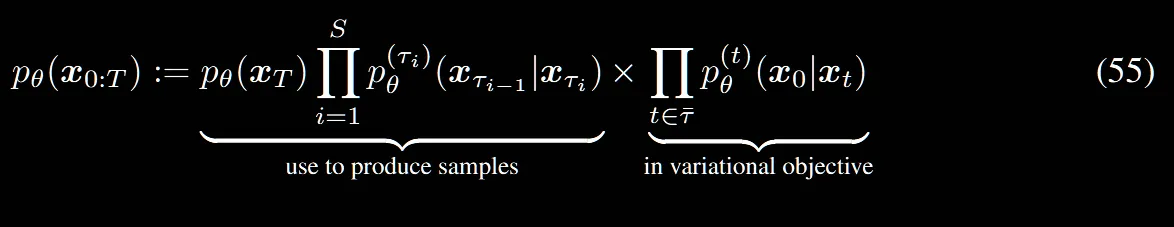
이부분 역시 수식을 하나하나 살펴보면서 이전 수식들과 비교해보겠습니다.

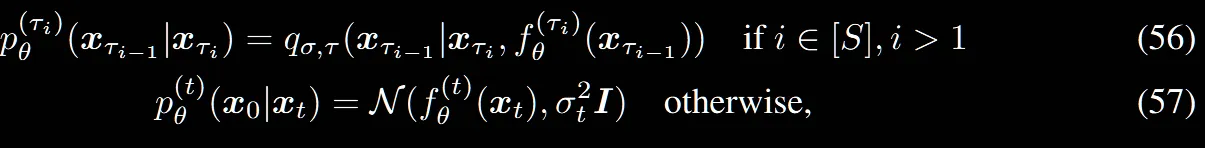
수식(10)에서 t=1일 때랑 아닐 때를 나눈것처럼 동일하게 작동합니다.

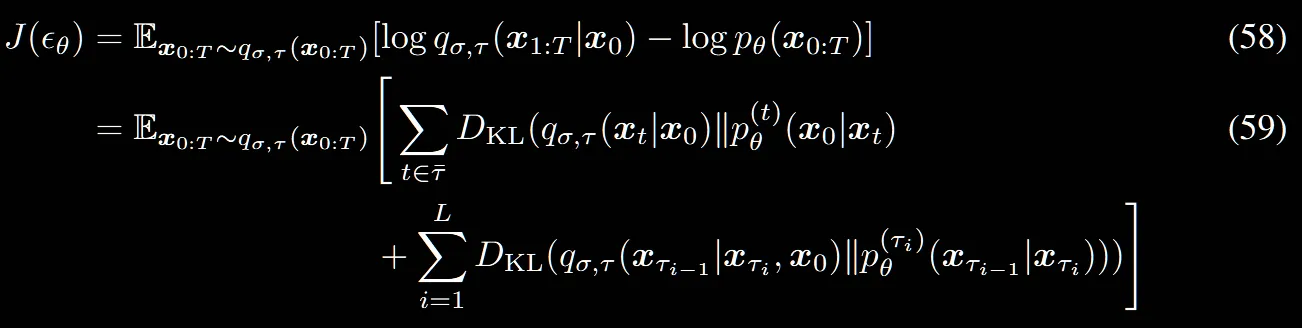
(58)번식은 (11)번식과 밑첨자만 다를 뿐 동일하게 작동합니다.

(58)번식의 첫번째 항에서는 선택되지 않은 단계에서의 분포가 학습한 분포와의 차이를 측정하고, 두번째 항에서는 선택된 단계에서의 원래분포와 모델이 생성한 분포 차이를 측정합니다.

요약하면 모든 부분에 대해서 비교하면서 학습이 진행되지만, 선택된 부분과 선택되지 않은 부분이 나눠져서 학습이 진행됩니다.

RELEVANCE TO NEURAL ODES

DDIM이 Neural ODE와 비슷하다는걸 설명하는 부분입니다.

자세한 내용은 추후 Neural ODE를 다룰 때 정확하게 정리하도록 하겠습니다.

EXPERIMENTS

DDPM과 DDIM의 훈련과정은 이전에 설명드렸던것처럼 동일하게 작동하고 차이점은 오직 몇개의 sampling을 진행할지 개수와 분산의 크기(0일 경우 deterministic)만 다릅니다.

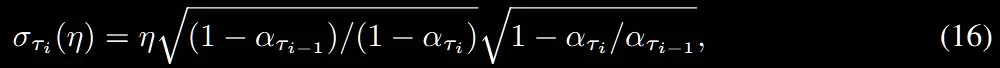
분산을 결정하는 수식은 위와 같습니다. η값이 1인경우 DDPM과 동일하게 작동하고, η값이 0인경우 완전 deterministic한 DDIM처럼 작동합니다.

FID Score: 생성된 이미지와 실제 이미지의 분포 간의 거리를 측정하는 지표로, 얼마나 생성된 이미지가 진짜 같은지를 나타냅니다. → 작을수록 좋다

• 실제 이미지와 생성된 이미지 모두 Inception 네트워크에 통과시켜 특징 벡터를 추출한 후, 두 분포의 평균과 분산 거리를 비교합니다.
• 계산이 복잡하고, 충분히 많은 샘플이 필요합니다.

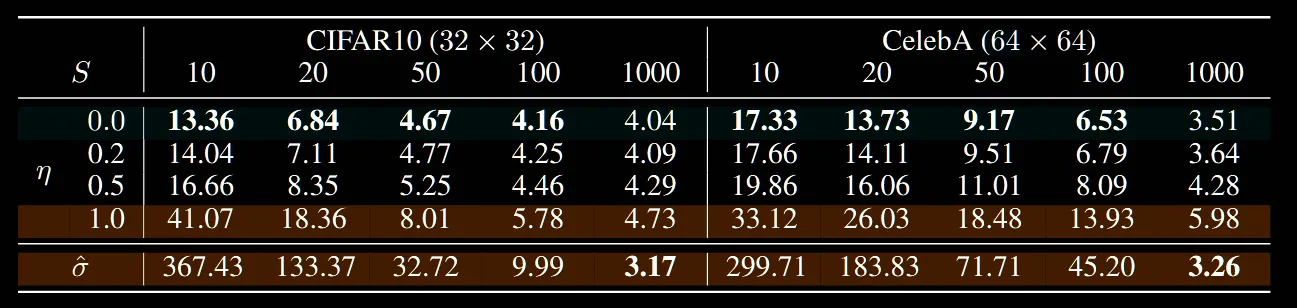
해당표는 FID Score를 비교한 표입니다. 확실히 η값이 작아질수록 성능이 좋아지고, step수가 작은 경우 차이가 더 뚜렷해지는 것을 확인할 수 있습니다.

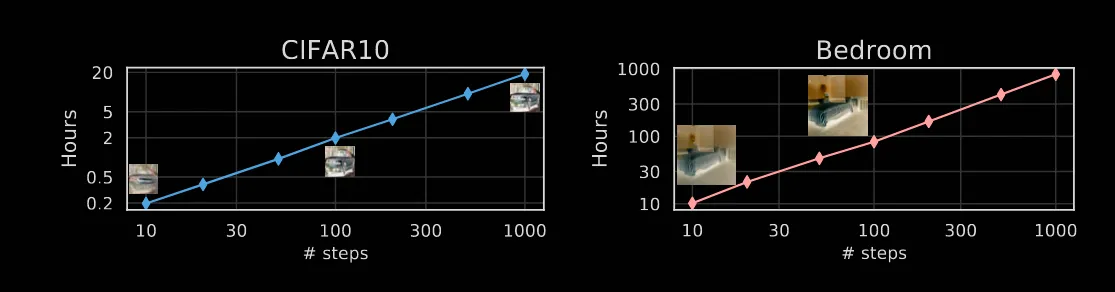
해당 그림은 왼쪽이 CIFAR10데이터셋을 step별로 학습하는데 걸리는 시간, 오른쪾이 Bedroom 데이터셋을 학습하는데 걸리는 시간입니다. DDIM은 10~100step에서의 결과가 DDPM의 1000step의 결과와 비슷하기 때문에 결론적으로 10배 많게는 50배의 시간을 절약할 수 있다고 설명하고 있습니다.

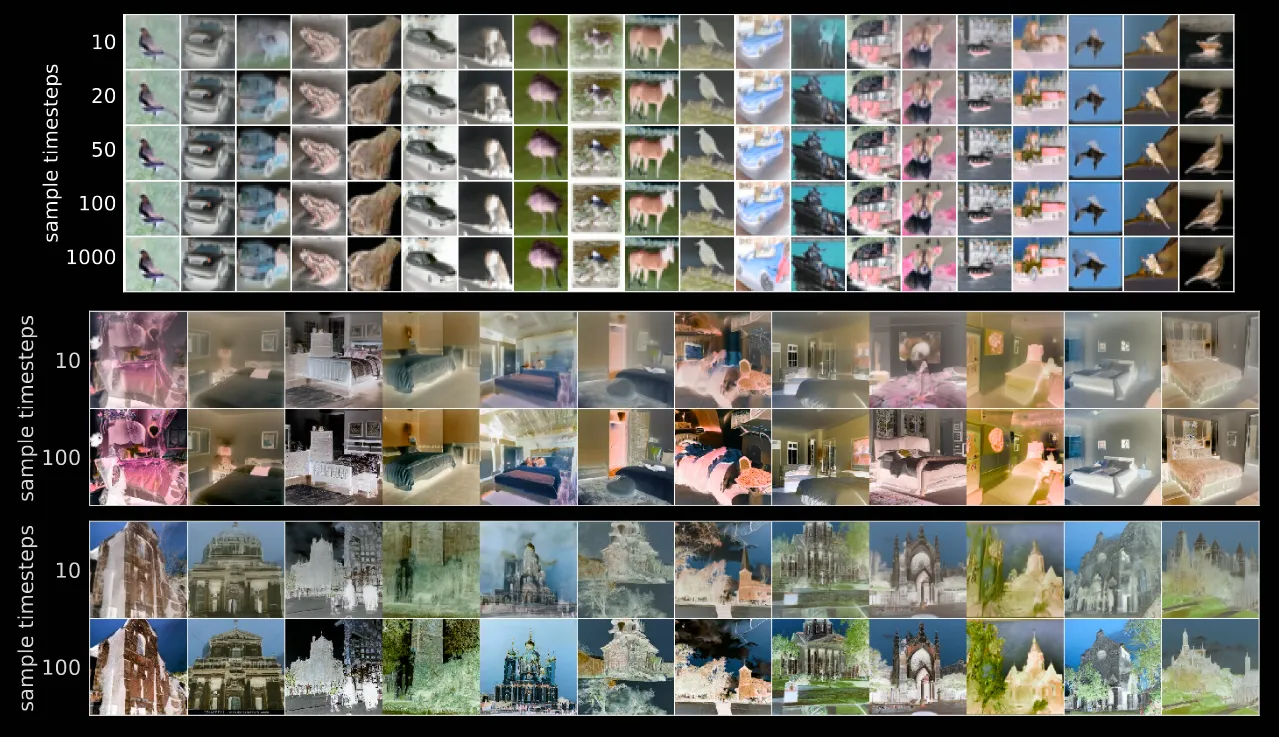
해당 그림은 동일한 latent $x_T$에서 시작하고 서로 다른 경로로 이동할 때의 결과를 나타냅니다. 결과를 보시면 10step만에 global한 정보는 거의다 잡아냈고, 이후의 과정에서는 디테일한 부분들을 찾는 것을 확인할 수 있습니다. 논문에서는 이를 기반으로 해당 $x_T$가 고품질 latent다 라고 설명했는데 그냥 저는 해당 부분을 작은 step에서 글로벌한 정보를 대부분 파악했고, 이후에는 로컬한 정보를 파악한다. 이를 이용해서 이미지 압축 기술도 적용할 수 있겠구나~ 라고 이해했습니다.