논문링크

https://arxiv.org/abs/2210.02747

저자소개 유튜브 영상

https://www.youtube.com/watch?v=5ZSwYogAxYg

Diffusion 모델보다 복잡한 데이터를 학습할 수 있는 Continous Normalizing Flows(CNFs)의 새로운 학습 방법(Flow Matching)을 제시하는 논문입니다. 논문의 순서를 그대로 설명하면서 필수적으로 읽어야되는 부분들은 따로 표시해두도록 하겠습니다. 단 해당 내용은 많은 배경지식을 필요로 하기때문에 이해에 도움이 되기위해서는 모든 부분을 읽는 것을 추천해드립니다.

Introduction

위의 사진은 Flow Matching을 적용해서 생성한 이미지들입니다.

Diffusion model들은 복잡한 데이터의 분포에서 정규분포로 변환하고, 다시 반대로 복잡한 데이터의 분포로 변환합니다. 이러한 제한적인 이동 방식 때문에 데이터 분포의 다양성이나 복합성을 충분히 반영하지 못합니다(표현력의 한계). 또한 다양한 경로(time step)를 통과하며 변화 시켜야하기때문에 훈련 시간이 매우 길어집니다.

따라서 일반적이고 결정론적인 형태인 Continuous Normalizing Flows(CNFs)를 사용했습니다. CNF는 임의의 확률 경로를 모델링 할 수 있어 더 다양한 데이터의 분포를 학습할 수 있습니다. 하지만 denoising score matching과 같은 효율적인 학습 방법이 존재하지 않습니다.

따라서 해당 논문에서는 Flow Matching(FM)이라는 방법으로 효율적이고 시물레이션이 필요 없는 방식으로 CNF 모델을 학습하는 방법을 제시했습니다. FM은 목표 vector field(데이터의 분포)를 따라 확률 경로를 생성하도록 CNF의 vector field를 학습하는 방식입니다.

PRELIMINARIES: CONTINOUS NORMALIZING FLOWS

해당 부분에서는 배경지식들을 설명하는 곳 입니다. 필수적이진 않지만 이해에 도움이 되는 내용들입니다.

Data: d차원 벡터 공간에 존재하는 포인트. $x = (x_1, …, x_d) ∈ R^{dn}$

Probability density path(p): 시간에 따라 변화하는 확률 밀도 함수 $p:[0,1] X R^d → R_{>0}$

• $p_t(x)$: 시간 t에서의 데이터 포인트 x에 대한 확률 밀도
• $∫pt(x)dx=1$

Vector Field: 데이터 공간의 각 위치에서 어떤 방향으로 얼마나 이동할지를 나타내는 정보

• $v: [0,1] X R^d → R^{dn}$

Flow(ϕ): 데이터를 시간에 따라 연속적으로 변환하는 함수. ODE(미분 방정식)으로 정의

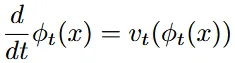
• $\frac{d}{dt}ϕ_t(x)$: 시간 t에서 데이터 포인트 x가 얼마나 빠르게 변화하는지
• $v_t(ϕ_t(x))$: 현재 데이터 위치에서의 vector field를 통해 데이터가 어떤 방향으로 이동하는지
• 데이터는 vector field가 지정하는 방향과 속도에 따라 이동하게 됩니다.

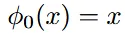
• t=0일 때 데이터 포인트가 변하지 않음

vector field with neural network: $v_t(x; θ)$ 의 식에서 θ가 학습 파라미터 입니다. 즉, neural network가 vector field를 학습하여 데이터의 이동 경로를 정의하고, 시간에 따라 데이터를 어떻게 변화시킬지를 모델링하는 방식입니다.

Continuous Normalizing Flow(CNF): 위의 vector field를 neural network로 나타낸 모델을 CNF라고 부릅니다. 이는 연속적인 시간 변화에 따른 데이터 변환을 모델링합니다. 즉, 간단한 데이터 분포에서 복잡한 분포로 변환하는 역할을 합니다.

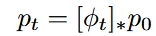
push-forward 방정식: 단순한 데이터 분포를 복잡한 분포로 변환하는 과정

• 초기 데이터 분포 $p_0$를 flow($ϕ_t$)를 통해 시간 t에서의 확률분포 $p_t$로 나타내는 것

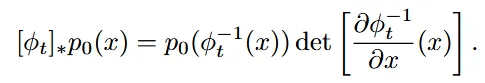
∗연산자는 위와 같이 나타납니다.

• $p_0(ϕ_t^{-1}(x))$: 역함수를 통해서 x가 초기 분포에서 어떤 위치로 매핑되는지를 계산
• $det[\frac{∂ϕ_t^−}{∂x}(x)]$: Jacobian 행렬식으로 데이터 변환시의 스케일 변화를 반영
  • 행렬식의 크기가 1보다 크면 부피가 확대, 작으면 부피가 축소된 것을 알 수 있다.

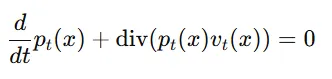
Continuity equation(연속 방정식): Vector field가 probability path를 생성하는지 테스트하는 방법

• 확률 밀도의 시간에 따른 변화를 설명하는 수식(Appendix B)

개인적인 의문 해결: Probability path vs Vector field vs Flow

Probability path: 간단한 데이터가 점차 복잡한 데이터 분포에 가까워지는 과정

Vector Field: 데이터가 목표 확률 분포로 이동하는 동안 각 데이터 포인트가 어디로, 얼마나 빠르게 이동해야 하는지

Flow: Vector Field에 따라 데이터가 이동한 전체 경로

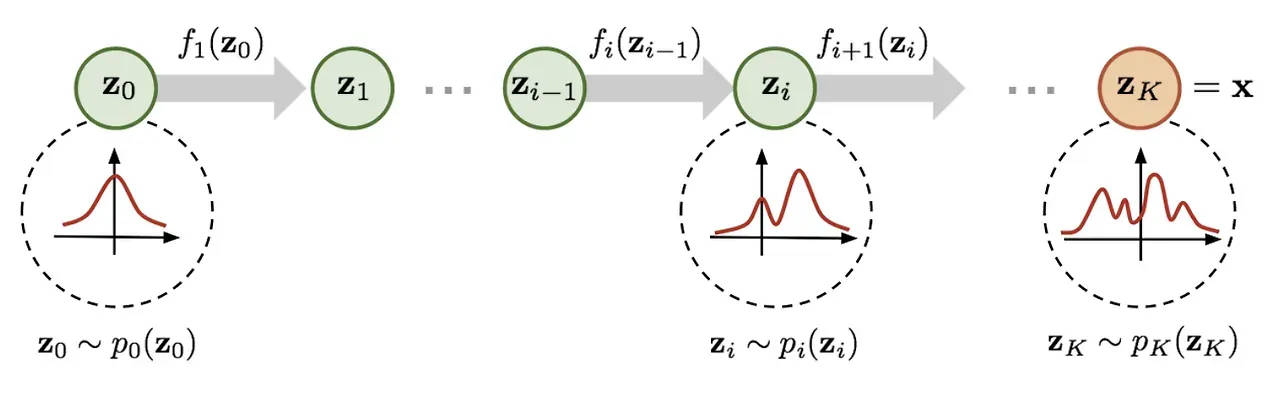
그림출처: https://bayesian-bacteria.tistory.com/4

그림을 기반으로 조금 더 자세히 말하면, f 함수가 vector field, 회색 화살표 전체가 probabilit path, 이 그림 자체가 flow라고 생각하면 된다.

Flow Matching[필수]

Flow Matching은 CNF를 학습하기 위한 새로운 목적 함수로 vector field를 학습하도록 하는 것

$q(x_1)$: 알려지지 않은 데이터의 분포(확률 밀도 함수)

• 우리는 $q(x_1)$에 대한 데이터 샘플을 갖고 있지만, 데이터 분포 함수 자체는 알지 못한다는 가정

$p_t$: probability path로서 시간에 따라 확률 분포가 어떻게 변하는지를 나타냅니다.

$u_t(x)$: vector field로서 시간에 따른 확률 분포 변화를 나타냅니다.

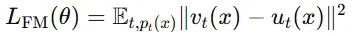
위의 수식은 CNF의 vector field인 $v_t$를 학습하는 방법입니다. 한마디로 $v_t$를 목표 vector field인 $u_t$와 같아지도록 regression 시키는 것입니다. 손실 함수가 0에 가까워지면 CNF 모델이 probability path($p_t(x)$)를 생성할 수 있습니다.

이를 직접 사용하기에는 어려움이 있습니다. 왜냐하면 $p_t$와 $u_t$를 정확히 알고 있지 않기 때문입니다.

CONSTRUCTING $p_t$, $u_t$ FROM CONDITIONAL PROBABILITY PATHS AND VECTOR FIELDS

이제 어떻게 정확히 알지 못하는 $p_t$와 $u_t$를 정의하는지 설명하도록 하겠습니다.

Conditional probability path(조건부 확률 경로, $p_t(x|x_1)$)

• t=0일 때 $p_0(x|x_1)$는 간단한 초기 분포 p(x)입니다.
• t=1일 때 $p_1(x|x_1)$는 평균이 $x_1$이고, 작은 표준편차를 가지는 정규분포 입니다.

Marginal probability path(주변 확률 경로, $p_t(x)$): 여러 조건부 확률 경로를 합친 결과

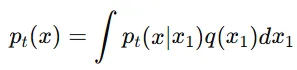
Marginal Vector field(주변 벡터 필드, $u_t(x)$)

• 조건부 벡터 필드($u_t(x|x_1)$)는 각 조건부 확률 경로 $p_t(x|x_1)$를 생성하는 벡터 필드

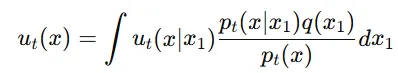
조건부 벡터 필드들을 모두 합친 것이 주변 벡터 필드

위의 수식에서 $u_t(x|x_1)$은 특정 샘플 $x_1$에 대해서 간단한 분포의 x가 어떻게 이동해야 하는지 나타냅니다. $\frac{p_t(x|x_1)q(x_1)}{p_t(x)}$는 가중치로, 각 데이터 샘플에 대한 conditional vector field($u_t(x|x_1)$)가 marginal vector field($u_t(x)$)에 얼마나 기여하는지를 결정합니다.

Theorem1: 조건부 문제들을 잘 정의하고 이를 마진화하여 합치면 전체적인 분포를 생성할 수 있는 유효한 벡터 필드를 얻을 수 있다는 것을 보장합니다.

CONDITIONAL FLOW MATCHING

Conditional flow matching은 Flow matching 목표와 동일한 최적화를 제공하면서 계산 복잡성을 줄이고 실용적으로 사용할 수 있는 대안적 접근입니다.

이전 단락에서 설명한 marginal probability path와 vector field는 적분 계산이 복잡하고 직접 계산하기 어려운 난해한 수식을 포함합니다. 따라서 Flow mathcing 목표를 계산하는 것은 비현실적입니다.

이에 따라 Conditional flow matching이라는 더 간단한 목표를 제안합니다.

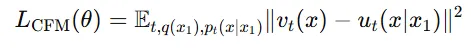
• t∼U[0,1]은 균등 분포를 따르는 시간입니다.
• $x_1\sim q(x_1)$은 데이터 분포에서 샘플링한 데이터입니다.
• $x \sim p_t(x | x_1)$은 조건부 확률 경로에서 샘플링한 데이터입니다.

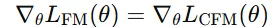
FM과 달리 CFM은 샘플 단위로 정의된 조건부 확률 경로와 조건부 벡터 필드를 사용해서 적분 계산을 수행하지 않습니다(Marginal을 사용하지 않아 샘플을 모두 더하는 적분 계산이 필요 없습니다). 더 간단한 계산 과정이지만 최적화 결과는 동일합니다.

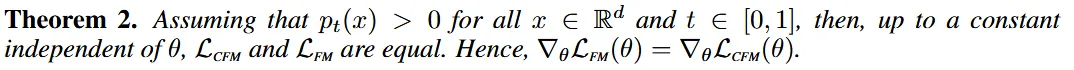
CFM과 FM이 동일하다는 것을 나타냅니다. 즉, 두 목표 함수의 기울기가 동일하므로 두 목표를 최적화하는 과정에서 같은 결과를 얻게 됩니다.

CONDITIONAL PROBABILITY PATHS AND VECTOR FIELDS[필수]

이전 단락에서 언급한 조건부 확률 경로를 어떻게 정의할지 설명합니다.

이 논문에서는 Gaussian 조건부 확률 경로를 사용해서 조건부 확률 경로를 정의합니다.

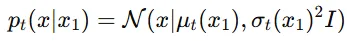
$μ_t(x_1)$: 시간에 따라 변화하는 평균 // $σ_t(x_1)$: 시간에 따라 변화하는 표준편차
t=0일 때 평균을 $μ_0(x_1)=0$, 표준편차를 $σ_0(x_1)=1$로 설정합니다 <정규 분포>
t=1일 때 평균을 $μ_1(x_1)=x_1$, 표준편차를 충분히 작은 값인 𝜎min으로 설정합니다.
조건부 벡터 필드는 조건부 확률 경로를 생성하기 위해 필요합니다. 그러나 특정 확률 경로를 생성하는 벡터 필드는 무수히 많습니다. 따라서 해당 논문에서는 가장 간단한 형태의 벡터 필드를 사용하고자 합니다.

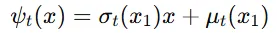
위의 수식은 가장 기본적인 벡터 필드를 사용한 Flow입니다.

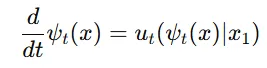
조건부 확률 경로를 생성하는 벡터 필드는 미분 방정식(ODE)를 통해 정의됩니다. 이 식은 시간에 따른 변화를 나타내는 방정식입니다. CFM loss function에 이 식을 대입하면 아래와 같은 형태로 나타낼 수 있습니다.

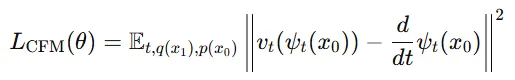
$ψ_t$가 단순한 선형 변환(affine map)이기 때문에, 벡터 필드($u_t(x|x_1)$)을 명시적으로 계산할 수 있습니다.

Theorem3: 벡터필드는 위와 같은 수식으로 계산할 수 있습니다(선형 변환을 이용). 이때 $σ_t^’(x_1)$와 $μ_t^’(x_1)$는 각각 시간에 따른 표준편차와 평균의 변화율을 나타냅니다. 이 벡터 필드는 조건부 가우시안 경로를 생성하며 이를 통해 우리가 원하는 확률 경로를 만들 수 있습니다.

SPECIAL INSTANCES OF GAUSSIAN CONDITIONAL PROBABILITY PATHS

$μ_t(x_1)$와 $σ_t(x_1)$는 미분가능한 함수면 모두 설정할 수 있습니다. 따라서 첫번째로 diffusion process를 이용하고, 두번째로 optimal transport solution을 이용해서 설명하겠습니다.

Example I: Diffusion Conditional Vector Fields

Diffusion모델은 복잡한 데이터 분포에서 노이즈를 추가하면서 단순한 분포로 변환하고, 이를 다시 노이즈를 예측하면서 원래 데이터로 복원하는 모델입니다.

Variance Exploding(VE) Path: 점점 큰 노이즈를 추가하는 방식

• 평균이 데이터 자체($x_1$)로 설정되고, 표준 편차는 시간이 지날수록 증가

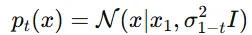
t=0일 때는 $σ_0$=0, t=1 일 때는 $σ_1$>>1로 설정됩니다. 평균은 원래 데이터 자체인 $x_1$로 설정

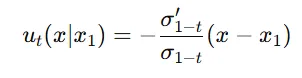
위의 과정을 Theorem3에 대입하면 위와 같은 수식이 나옵니다. 여기서 벡터 필드는 데이터가 $x_1$으로 수렴하도록 하는 방향을 제시합니다.

Variance Preservering(VP) Path: 노이즈를 추가하는 과정에서 데이터의 분산을 어느 정도 유지. 즉 원래 데이터의 정보가 더 많이 남아있도록 하는 방식입니다.

• 평균이 일정 비율로 줄어들고, 그에 따라 표준편차도 조절

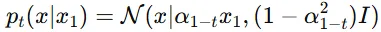
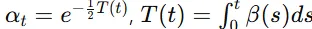
평균이 $\alpha_{1-t} x_1$로 설정되어 시간이 지남에 따라 감소합니다. 표준편차는$\sqrt{1 - \alpha_{1-t}^2}$로 설정되어 데이터가 일정 부분 분산을 유지하면서 변하도록 합니다.

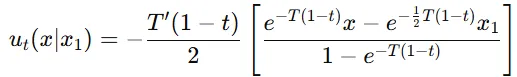
역시 위의 과정을 Theorem3에 대입하면 위와 같은 수식이 나옵니다. 여기서 벡터 필드는 데이터가 원래 데이터로 수렴하도록 하는 방향을 나타냅니다.

이와 같은 방법은 기존 diffusion model과는 다르게 유한한 시간안에 완전히 순수한 가우시안 분포로 갈 수 있습니다. 따라서 근사없이 더 정확하고 효율적인 학습이 가능합니다.

Example II: Optimal Transport conditional VFs

Optimal Transport(OT)는 데이터 간의 이동을 최소화하는 경로를 찾는 과정입니다. 즉, 평균과 표준편차를 선형적으로 변화시켜 최적의 경로를 찾는 과정입니다.

평균($\mu_t(x_1)$): 시간 t에 따라 선형적으로 변하며, $μ_t(x_1) = tx_1$로 정의됩니다.

표준편차($\sigma_t(x_1)$): 시간에 따라 선형적으로 감소하며, $σ_t(x_1)=1−(1−σ_{min})t$로 정의됩니다.

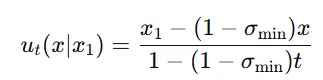
Theorem3에 역시 대입하면 위와 같은 식이 됩니다. 벡터필드는 역시 데이터가 점차적으로 원래 데이터로 이동하도록 유도합니다.

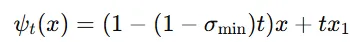
위의 조건부 벡터 필드에 대응하는 조건부 흐름은 위와 같은 수식으로 나타납니다.

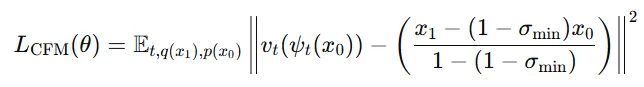
또한 CFM 손실 함수는 위와 같은 형태로 나타납니다.

Optimal Transport는 결론적으로 단순한 분포와 복잡한 분포 사이의 최적 이동 경로를 나타냅니다. 이는 항상 직선으로 이동합니다.

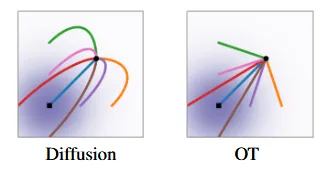
Diffusion 모델에서는 여러개의 경로가 곡선으로 나타나 있습니다. 경로의 끝에서 보면, 목표 지점에 도달하기 위해 과도하게 이동(overshoot) 한 후 다시 되돌아오는 움직임을 보입니다. 이로 인해 샘플에 도달하기 위한 backtracking이 발생합니다.

OT모델에서는 모든 경로가 직선 형태로 나타나 있으며, 시작점에서 목표 지점까지 일관된 직선 경로를 따릅니다. 즉 불필요한 추가 이동이 없습니다.

그림의 색깔은 벡터의 크기를 나타내며, 파란색은 크기가 큰 벡터, 빨간색은 크기가 작은 벡터를 의미합니다. 벡터의 방향은 화살표의 방향을 참고하면 됩니다.

diffusion path에서 초기에는(t=0) 각 점에서 벡터가 중앙으로 수렴하는 형태를 띠며, 벡터의 크기는 비교적 일정합니다. 벡터 필드의 방향이 일정하지 않고 시간이 지남에 따라 변하므로, 이 경로를 추정하는 모델이 복잡해집니다.

OT path에서 벡터 필드의 방향이 시간에 따라 일정하게 유지됩니다.각 시점에서 벡터는 중앙에서 방사형으로 퍼져나가는 형태를 가지며, 시간이 지나도 방향이 바뀌지 않습니다. 즉, 모델이 이를 학습하는 것이 상대적으로 쉬워집니다.

사진출처: https://bayesian-bacteria.tistory.com/4
시간이 지남에 따라 데이터의 분포를 시각화 한 것입니다. 맨오른쪽 OT 모델이 가장 빠르게 데이터의 분포를 찾는 것을 확인할 수 있습니다.

RELATED WORK

Continous Normalizing Flows에서 ODE의 적분에는 많은 시간이 걸립니다. 이를 해결하기 위해서 augmentation이나 regularization을 추가하는 방식등 다양한 연구가 나왔습니다. 이러한 연구들은 ODE를 regularize한 것이지 학습 알고리즘 자체를 바꾼 것이 아닙니다.

CNF의 학습 속도를 높이기 위한 방법으로 simulation-free CNF training frameworks가 개발됐습니다. 하지만 여전히 적분 계산의 힘듦, biased gradients 문제들이 있습니다.

하지만 Flow Matching 해당 논문은 시물레이션도 필요 없이 CNF를 학습할 수 있고, 간단하고 빠르게 학습하면서 unbiased gradient입니다.

기존 diffusion 모델은 denoising score matching을 통해서 무작위 노이즈를 제거하면서 학습하는 과정입니다. 이를 통해서 unbiased gradient를 제공합니다. CFM은 diffusion을 기반으로 설계 됐지만, 벡터 필드 자체를 직접 매칭하는 접근 방식을 일반화한 것입니다. Flow Matching에서는 처음으로 diffusion 과정 없이 확률 경로를 직접 다룰 수 있는 가능성을 제시합니다.

EXPERIMENTS

DENSITY MODELING AND SAMPLE QUALITY ON IMAGENET

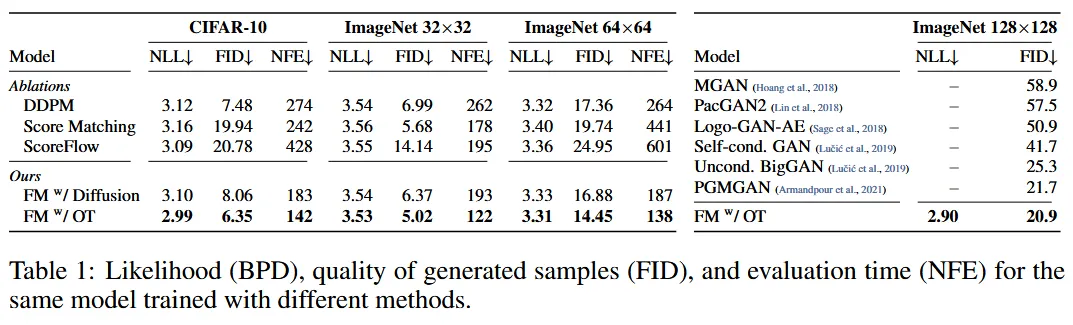
Diffusion loss 종류

• DDPM: 복잡한 데이터의 분포에 노이즈를 점진적으로 추가하여 정규분포로 변환한 후, 그 역과정을 학습하여 원래의 데이터 분포를 재구성하는 것
• Score Matching: 각 단계에서 데이터 분포의 Score 함수(확률 밀도 로그 미분)를 직접 학습하여 샘플을 생성하는 방식
• ScoreFlow: Score Matching을 활용하여 연속적인 확률 흐름을 학습하는 방식

평가 지표

• NLL(Negative Log-Likelihood): 모델이 데이터 분포를 얼마나 잘 추정하는지 평가하는 지표
• FID(Frechet Inception Distance): 생성된 이미지와 실제 이미지의 분포 간 거리를 측정합니다.
• NFE(Number of Function Evaluations): Adaptive ODE Solver가 주어진 수치적 허용 오차를 충족하기 위해 함수 평가를 수행한 횟수의 평균. 얼마나 학습이 빠르고 효율적인지를 나타냅니다.

결론: Flow Matching의 Optimal Transport의 성능이 모든 부분에서 가장 좋게 나왔습니다.

• 단 오른쪽 ImageNet 128x128에서는 IC-GAN의 성능이 더 좋아 이는 표에서 제외했습니다.

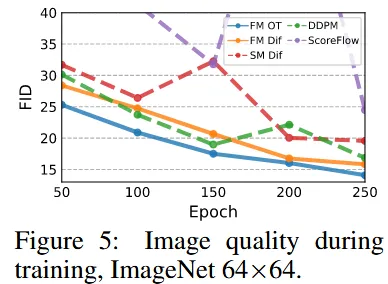
학습 속도에 대해서 나타낸 그림으로 파랑색 선인 FM의 OT가 성능도 가장 좋고, 적은 Epoch에 대해서도 다른 모델들보다 좋은 결과를 내는 것을 알 수 있습니다.

SAMPLING EFFICIENCY

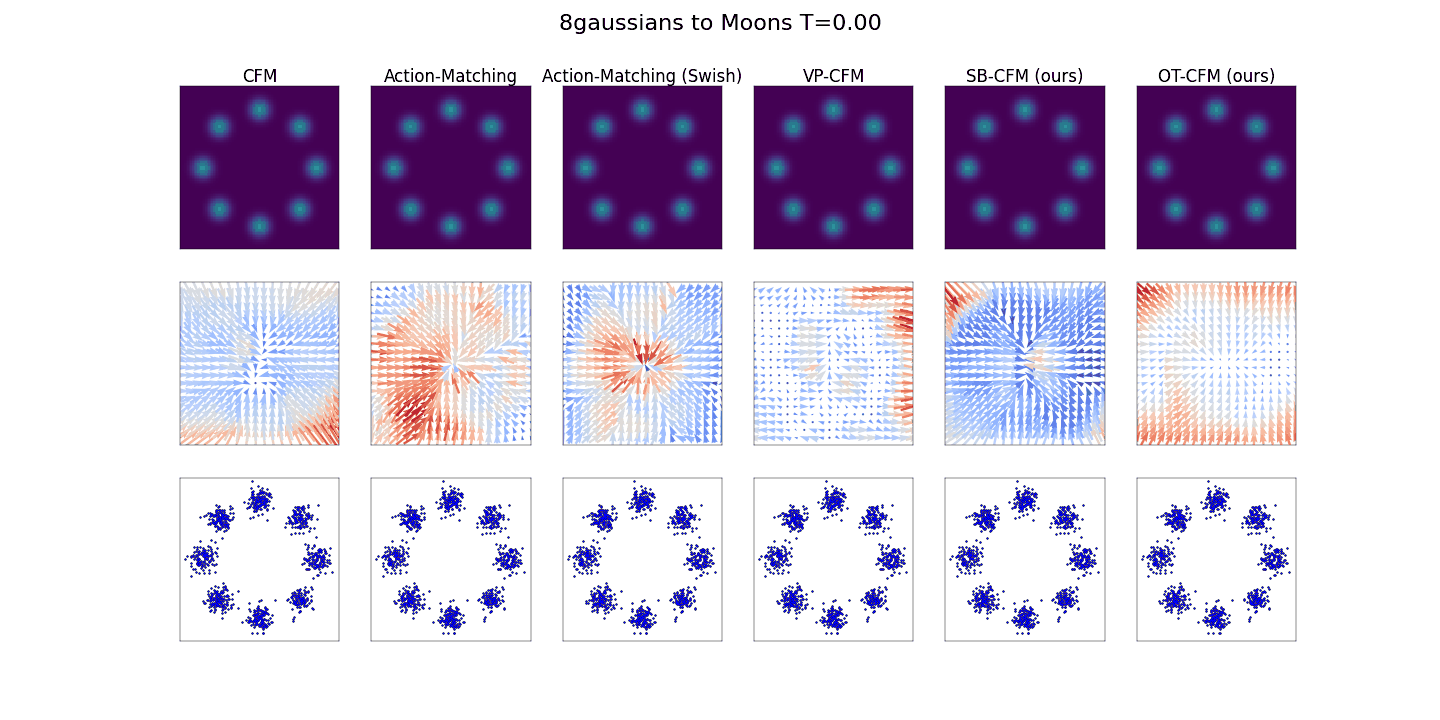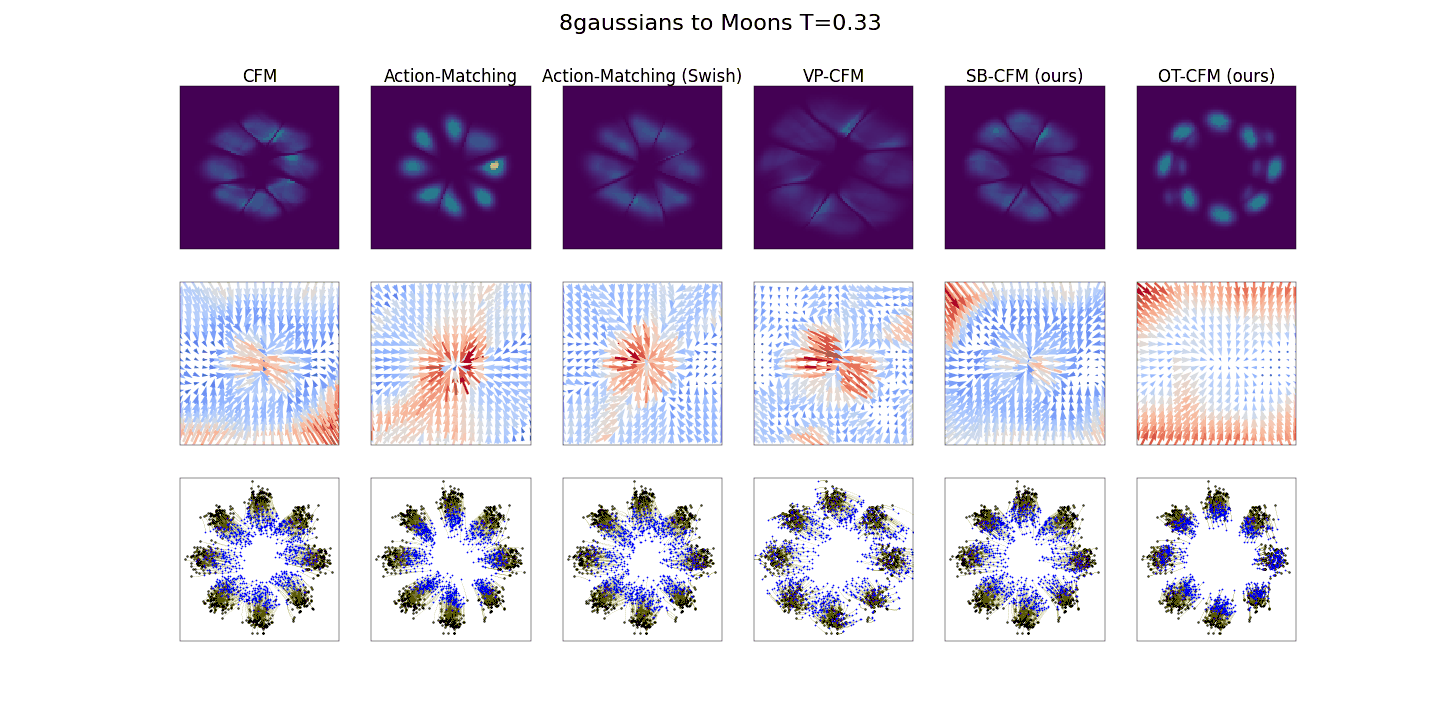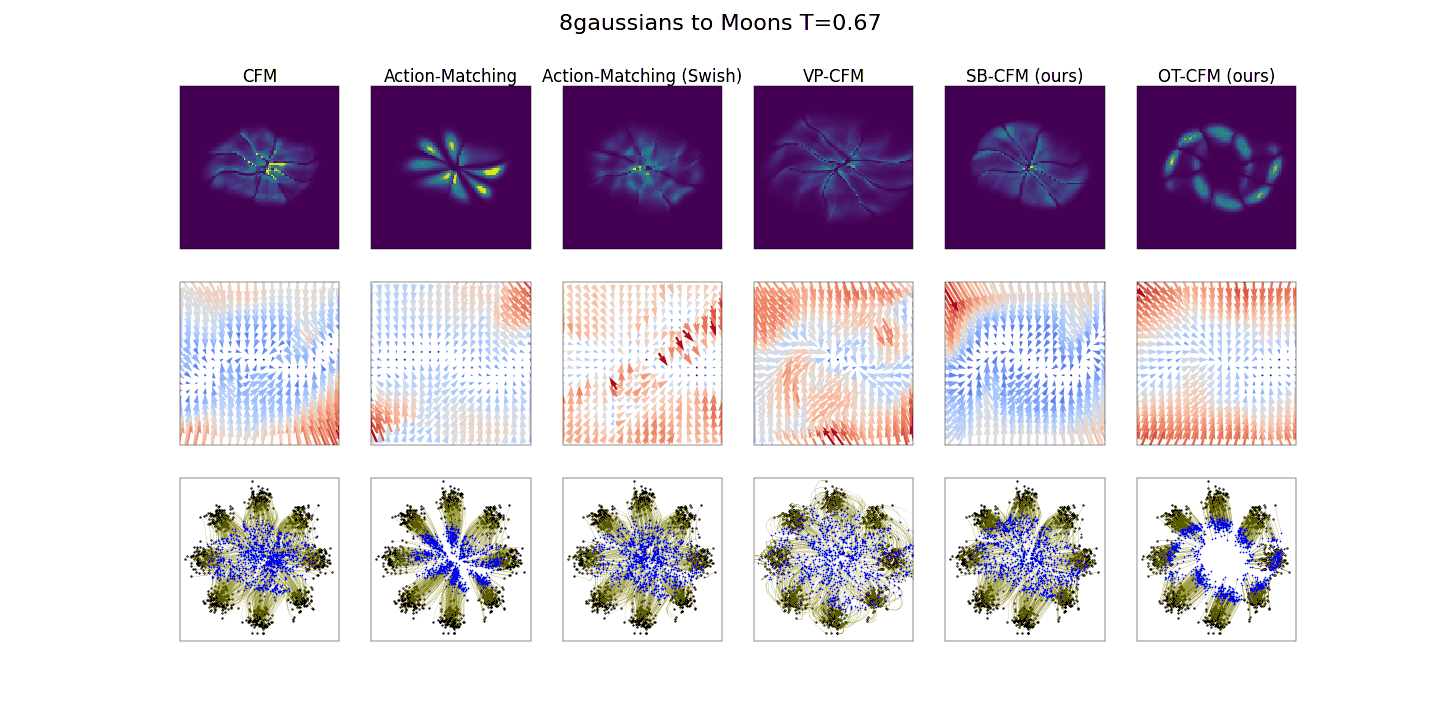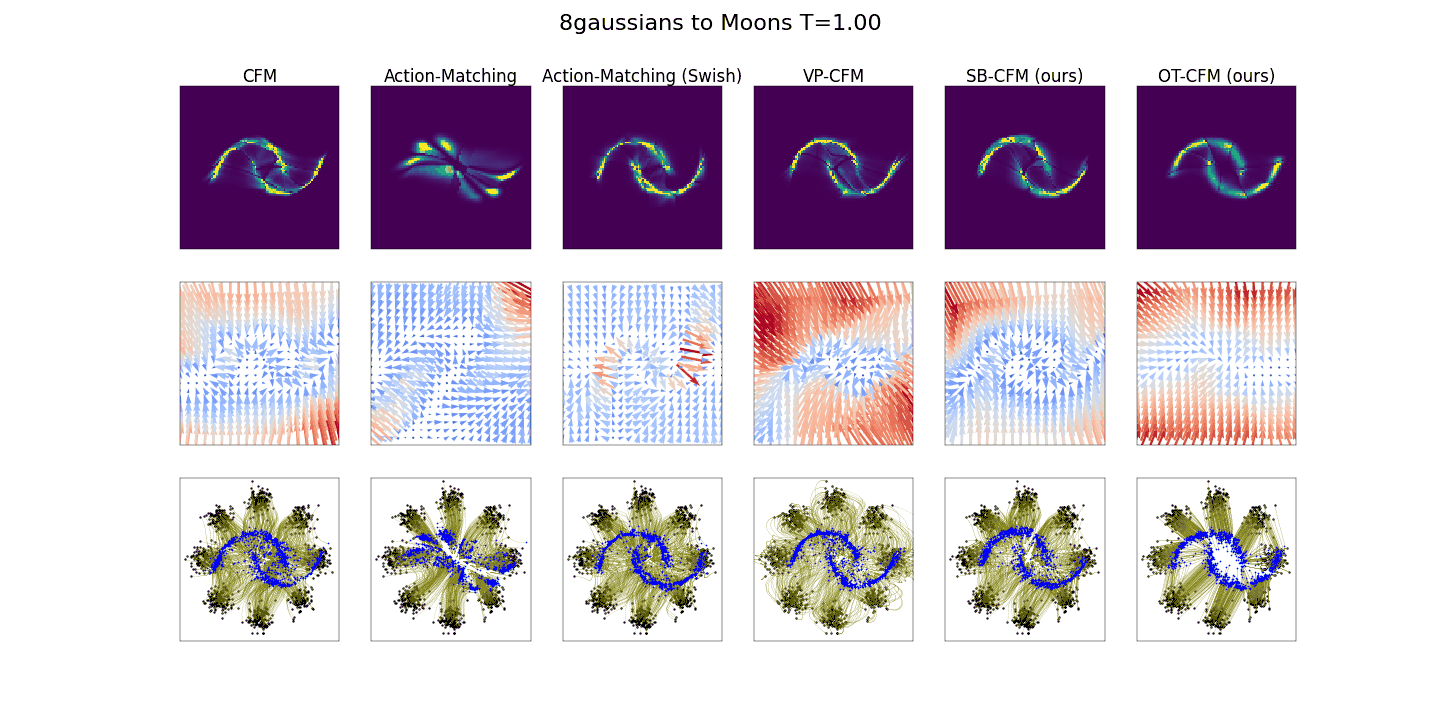
SDE(Stochastic Differential Equation)은 데이터 변환에 랜덤성을 포함한 미분 방정식을 사용하여 샘플링하는 과정인데, 계산 비용이 높고 비효율적이기 때문에 ODE Solver를 이용해서 샘플링을 진행했습니다. Diffusion 경로와 OT 경로의 차이점에 대해서 아래 그림을 이용해서 설명했습니다.

첫번째와 두번째 사진 즉 Diffusion경로에서는 거의 마지막에서 이미지 생성이 이루어지지만, 맨 오른쪽 사진인 OT 경로를 이용할 경우 상대적으로 일찍 이미지가 형성됩니다. 이를 기반으로 OT 경로가 더 효율적으로 보일 수 있습니다.

다양한 함수로 학습된 CNF의 경로를 시각화 한 것입니다. 첫번째와 두번째 diffusion 경로를 이용할 때 체커보드 패턴이 조금씩 형석되지만, OT 경로는 훨씬 더 빠르게 체커보드 패턴이 나타나는 것을 볼 수 있습니다. 오른쪽 사진에서 NFE가 작을 때도 더 효율적으로 체커보드 패턴을 생성할 수 있는 것을 볼 수 있습니다.

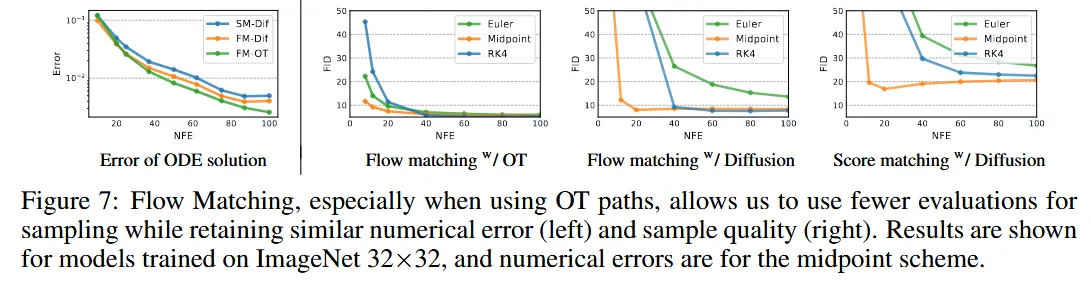
모델의 효율성 측면을 시각적으로 비교한 사진입니다.

왼쪽 그래프에서는 ODE Solver에서의 오류를 측정한 것으로, y축은 MSE, x축은 NFE를 나타냅니다. FM-OT 모델이 다른 모델보다 더 빠르게 오류가 감소하는 것을 알 수 있습니다.

오른쪽 그래프에서는 FID와 NFE의 관계를 나타낸 것입니다. OT 경로를 이용할 때 FID가 가장 빠르게 감소하며 낮은 NFE에서도 좋은 품질을 보여주는 것을 확인할 수 있습니다.

CONDITIONAL SAMPLING FROM LOW-RESOLUTION IMAGES

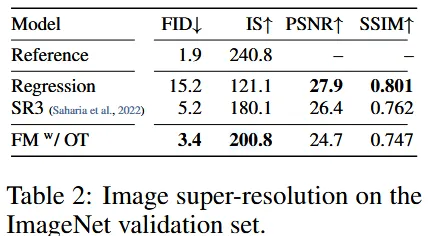
해상도를 64에서 256으로 높였을 때의 결과 비교 사진입니다.

• Reference: 원본 검증 세트의 결과(Ground Truth)
• Regression: 회귀 방법을 사용한 결과. PSNR과 SSIM이 좋지만, FID와 IS가 상대적으로 낮습니다. 이는 화질은 좋지만, 생성된 이미지의 분포가 실제 데이터와 잘 맞지 않음을 의미합니다.
• SR3: 다른 논문에서 제안된 모델로 FID와 IS가 Regression에 비해 개선되었지만, PSNR과 SSIM은 감소
• FM-OT: FID와 IS가 위의 2가지 모델보다 좋지만, PSNR과 SSIM은 떨어진 것을 확인할 수 있습니다.

요약하면, FM-OT 모델은 이미지 분포와 다양성 측면에서 뛰어난 성능을 보이지만, 화질면에서는 성능이 좋지 않음을 확인할 수 있습니다.

코드

https://github.com/gle-bellier/flow-matching/tree/main
해당 링크의 ipynb에서 수식에 대해서 코드를 한줄한줄 자세히 설명해줘서 해당 부분을 잘 따라가면 될거같습니다.
마지막에 npy를 저장하는게 있는데 이를 mp4로 시각화하는 코드만 소개하도록 하겠습니다

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation

# 저장된 .npy 파일 로드
filename = "swiss_ot_10000_100.npy"  # 저장된 파일명
data = np.load(filename)  # (N_STEPS + 20, N_SAMPLES, 2) 형태의 배열

# 시각화를 위한 Figure 설정
fig, ax = plt.subplots(figsize=(8, 8))
scatter = ax.scatter(data[0, :, 0], data[0, :, 1], alpha=0.3, s=10)
ax.set_xlim(-3, 3)  # 데이터 분포에 맞게 x 범위를 설정합니다.
ax.set_ylim(-3, 3)  # 데이터 분포에 맞게 y 범위를 설정합니다.
ax.set_xlabel('x-axis')
ax.set_ylabel('y-axis')
ax.set_title('Time Step: 0')

# 업데이트 함수 정의 (각 프레임에서 데이터를 업데이트)
def update(frame):
    scatter.set_offsets(data[frame])  # 현재 time step의 데이터로 scatter plot 업데이트
    ax.set_title(f'Time Step: {frame}')
    return scatter,

# 애니메이션 생성
ani = animation.FuncAnimation(fig, update, frames=len(data), blit=True, interval=100)

# 애니메이션 저장 또는 보여주기
ani.save('sampling_animation.mp4', writer='ffmpeg', fps=10)  # mp4 파일로 저장 (ffmpeg 필요)
plt.show()

코드 결과는 위와같습니다. 이상으로 리뷰를 마치겠습니다.