논문 링크

https://arxiv.org/pdf/2209.03003

Abstract

Rectified Flow는 두 데이터 집합 간을 이동할 때 가장 짧고 직선 경로를 따라 이동하도록 학습하는 방법으로, 데이터 생성 및 변환을 더 효율적으로 할 수 있는 모델입니다. 이를 통해 계산 비용을 줄이고 정확성을 높일 수 있으며, 여러 이미지 생성 및 변환 작업에서 좋은 결과를 보여줍니다.

Introduction

비지도학습은 지도학습과 달리 입력과 출력값이 매칭되지 않기 때문에 학습에 어려움이 있습니다. 비지도학습의 핵심은 데이터 분포의 차이를 학습하는 것입니다. 생성 모델(GAN, VAE)나 domain transfer(image-to-image translation) 같은 모델들의 공통점은 하나의 데이터 분포에서 다른 분포로의 이동입니다.

Transport Mapping Problem

두 개의 데이터 분포 (π0와 π1)가 주어졌을 때, 이를 연결하는 Transport Map을 찾는 문제를 다룹니다. 예를 들어, 개 이미지를 고양이 이미지로 변환하는 과정에서 Z0가 π0에 해당하는 개 이미지이고, 전환 맵 T를 통해 Z1으로 변환했을 때 Z1이 π1의 분포와 같아지는 것을 목표로 합니다.

Transport Mapping 방법으로서 GAN 모델에서는 신경망을 이용했지만, numerical instability과 mode collapse 문제가 발생했습니다.

최근에는 Flow 모델에서 ODE이나 SDE을 사용하는 방법들이 도입되었습니다. 이러한 방법들은 수학적 구조를 활용해 더 효율적으로 학습하고, GAN의 문제를 해결했습니다. 하지만 많은 계산 비용이 발생하고, 하이퍼파라미터를 적절히 설정해야 한다는 단점이 존재합니다.

이 문제를 해결하기 위해 최적의 경로를 제공하는 Optimal Transport (OT)가 도입되었지만, 고차원 데이터나 대규모 데이터에 대해서는 계산이 느리다는 단점이 있습니다. 추가적으로, OT 방법이 항상 최적의 경로를 찾는다고 하더라도 학습 성능이 보장되지 않을 수 있습니다.

Contribution

Rectified flow는 두 데이터 분포를 연결하는 ODE 기반 모델로, 가능한 한 직선 경로를 따라 이동하여 데이터를 변환합니다. Unconstrained least squares optimzation procedure를 기반으로 학습해서 계산 비용이적고, 기존의 오류들을 해결했습니다.

위의 2개의 행은 이미지 생성 과정을, 아래 2개의 행은 image-to-image(person → cat)을 보여주는 그립입니다. 적은 Euler steps으로도 좋은 결과를 낼 수 있는 것을 확인할 수 있습니다.

Method

Overview

Rectified flow

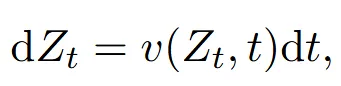
Rectified flow는 두 데이터 분포를 연결하는 ODE 모델입니다.

Drif force(v)는 X0에서 X1으로 가는 가능한 한 직선 경로를 생성하는 함수입니다.

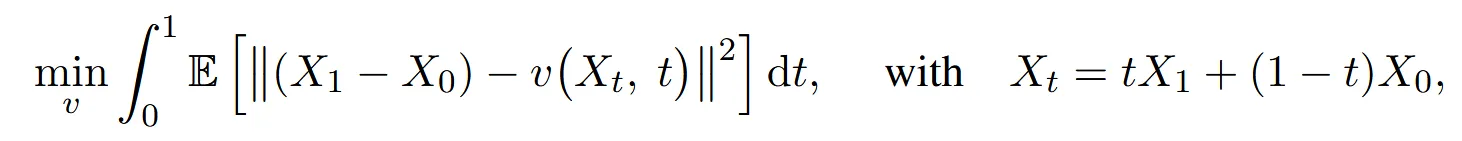
$X_t$가 $X_0$과 $X_1$의 linear interpolation(선형 보간)으로 나타낸 식입니다. $X_t$만 이용할 경우 항상 미래의 정보 $X_1$을 알아야 한다는 문제가 발생하므로 이를 학습하기 위한 drift force(v)를 neural network나 nonlinear model로 설정해둔 것입니다. v를 학습하고 나면 역방향인 X1에서 X0로의 변환도 가능합니다.

Flows avoid crossing

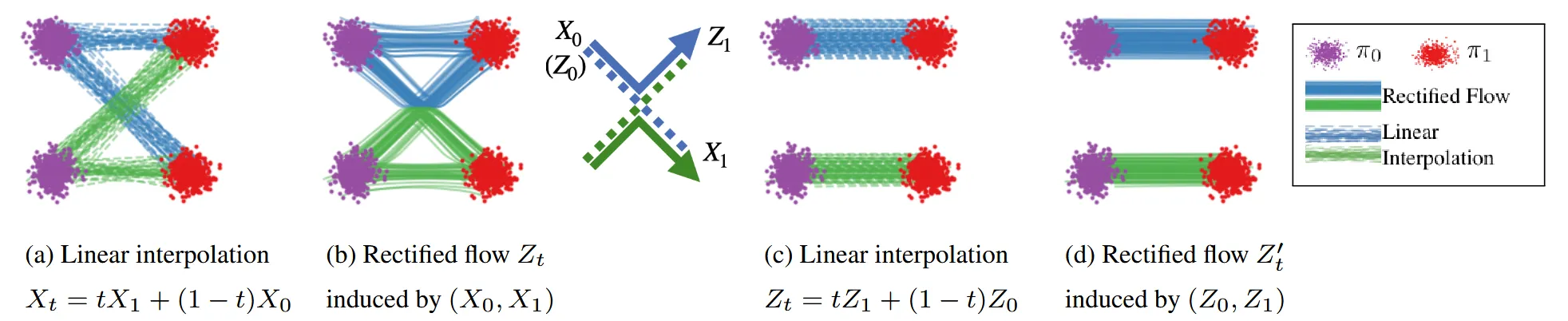
(a) 그림을 보면 보라색 점에서 빨간색 점으로 가는 경로는 여러가지가 존재합니다. 이렇게 서로 교차하면서 다양한 방향으로 이동하는 것은 non-causal 경로이며, 각 경로가 명확히 결정되지 않은 상황입니다. ODE는 deterministic(결정론적)이기때문에 여러가지 경로가 존재하면 안됩니다.

따라서 drift force(v)를 학습하게 됩니다. 각 선들은 최대한 직선거리(최단거리)를 생성하도록 학습되기 때문에 (b)처럼 파란색 선들은 위로 초록색 선들은 아래로 향하게 되는 것을 알 수 있습니다.

정리하면, (a)와 (c)처럼 단순히 linear interpolation을 사용하면 교차되는 점들이 존재하고, 이는 직선거리도 아니고 하나의 경로로 정의되지 않기 때문에 Rectified flow 즉 drift force(v)를 학습하면서 하나의 경로를 나타내도록 합니다.

어떻게 학습하냐라고 했을 때는, 위의 수식에서 두 점 사이의 최소 거리를 달성하도록 학습되기 때문에 자연스럽게 최소 거리를 나타내도록 하나의 경로로 나타낼 것입니다. (더 자세한 수식은 추후 설명)

Rectified flows reduce transport costs

데이터 분포 $X_0$과 $X_1$을 연결하는 수많은 분포에서 Redctify를 이용해서 최적의 경로를 설정하면 $Z_0$과 $Z_1$로 나타낼 수 있습니다. 이때 $Z_0$과 $Z_1$을 연결하는 선들은 다른 선들에 비해서 비용이 항상 작다는 것입니다(Theorem 3.5). 상식적으로 하나의 점에서 다른 점으로의 최단 거리는 두 점을 잇는 직선이고, 나머지 모든 경로는 해당 직선보다 길기 때문에 이해하실 수 있을 것입니다.

Straight line flows yield fast simulation

Inputs: $X_0$와 $X_1$의 데이터 분포들이 입력값으로 들어가게 됩니다. 이전에 설명한 것처럼 두 데이터 분포를 잇는 선들은 다양하고 non-causal한 경로일 것입니다.

Training: 데이터 분포들이 직선 경로를 만들도록 학습이 진행됩니다.

Sampling: θ를 기반으로 학습한 drift(v)를 기반으로 ODE $Z_t$를 생성합니다. 시작점 $Z_0$에서 시작해서 한번 진행할 때마다 값이 1씩 증가합니다.($Z_0$ → $Z_1$)

Return: 최종적으로 t번째 Z를 반환합니다.

Reflow: Sampling에서 설명한 것처럼 RectFlow를 한번 진행할 때마다 더 정교한 직선 경로를 나타낼 수 있도록 하면서 값이 1씩 증가합니다. 시작점은 $Z_0$입니다.

Distill: k번째 Rectified Flow를 학습한 후 이를 압축한 모델($\hat{T}$)을 말합니다.

이러한 반복적인 Rectified flow를 거치면서 transport cost도 감소하고, 더 정교한 직선 경로를 생성할 수 있습니다. 이렇게 반복 작업을 통해 완전하게 학습된 경우 하나의 Euler step 만으로도 좋은 결과를 얻을 수 있게됩니다.(Introduction 그림)

Main Results and Properties

$X_t$가 x시점일 때 어느 방향으로 이동하는 것이 최적인지를 결정하기 위해 모든 경로의 방향 벡터의 평균을 취합니다. 즉 $v_X(x,t)$는 현재 위치에서 앞으로 어떻게 이동할지를 결정적으로 알려주는 역할을 합니다.

이렇게 하면, ODE 방정식을 풀어가며 각 시간 t에 대해 $Z_t$가 어디로 이동해야 할지 명확하게 알 수 있게 됩니다.

Marginal preserving property

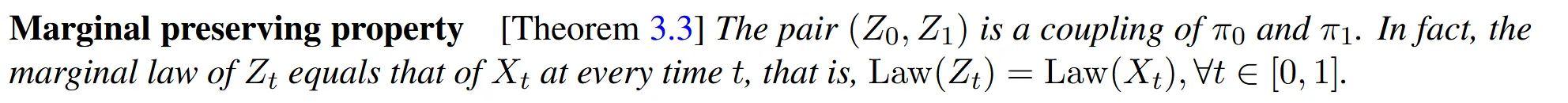
Theorem3.3: 시간 t에서 $Z_t$의 확률분포와 $X_t$에서의 확률 분포가 동일하다.

예를 들어, 개에서 고양이로 변하는 경로$X_t$와 $Z_t$는 서로 다른 경로를 갖고 있지만, 특정 시간에 얼마나 많은 개가 고양이로 변하고 있는지가 같다는 뜻입니다. 즉, 같은 시간에 개와 고양이가 몇 마리씩 변하고 있는지는 동일하게 유지된다는 것입니다.

일관된 변환을 하기 위해서는 동일한시간에 동일한 데이터가 변환되어야합니다. 위의 이론에서 동일한 시간에서 다른 경로라고 할지라도 동일한 양만큼의 변환이 이루어진다는 것을 확인했으므로, 결과적으로 문제가 없다는 것을 알 수 있습니다.

이 이론은 직관적으로 질량 보존의 법칙과 동일하게 작동합니다. 위 그림은 확률 밀도 보존을 나타내는데, 특정 위치와 시간에서 확률 밀도가 유입되는 양과 유출되는 양이 같다는 것을 의미합니다. 왼쪽 Rectified Flow와 오른쪽 Linear Interpolation 경로 모두에서 특정 지점에서 유입량과 유출량이 동일하므로 분포 밀도가 같다고 할 수 있습니다.

$Z_t$와 $X_t$의 Marginal distribution은 동일하다고 위에서 설명했지만, Joint distribution(전체 경로)는 다를 수 있습니다.

$X_t$는 non-casual(미래의 정보를 알고 있어야 현재 상태를 결정할 수 있다.)하고 non-Markov process(현재 상태가 오로지 과거의 바로 이전 상태만이 아니라 더 이전의 정보까지 의존할 수 있다.)입니다. 즉 $X_0$와 $X_1$의 결합은 확률적 결합으로 일관되지 않습니다.

반면에 $Z_t$는 casualize(미래 정보 필요 하지 않고)하고 Markovianizes(현재 상태만으로 다음 상태를 결정할 수 있고)하고 derandomizes(확률적인 요소를 제거) 합니다.

즉, 전체 경로를 바꾸면서도, 각 시간 t에서의 분포는 동일하게 유지하는 것입니다. 이를 통해 결과적으로 두 분포를 잘 연결하는 일관된 변환 경로를 제공할 수 있습니다.

Reducing transport costs

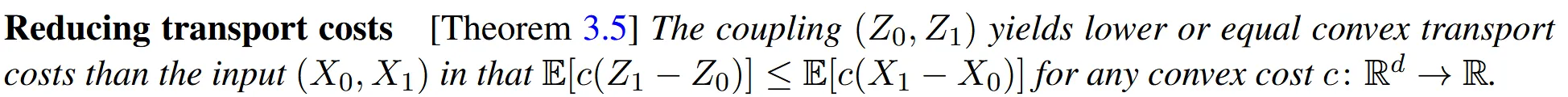
transport cost는 일반적으로 거리에 비례해서 증가합니다. 따라서 Rectify를 거친 Z는 Linear Interpolation 값보다 항상 작거나 같습니다.

위의 그림을 보면 조금더 직관적으로 이해할 수 있을 것입니다. ()는 triangle inequality(삼각형에서 가장 긴 변보다 나머지 두변의 합이 더크다), (*)는 경로를 rewiring(재배치)하면서 더 효율적으로 이동한다는 것을 나타냅니다.

Reflow, straightening, fast simulation

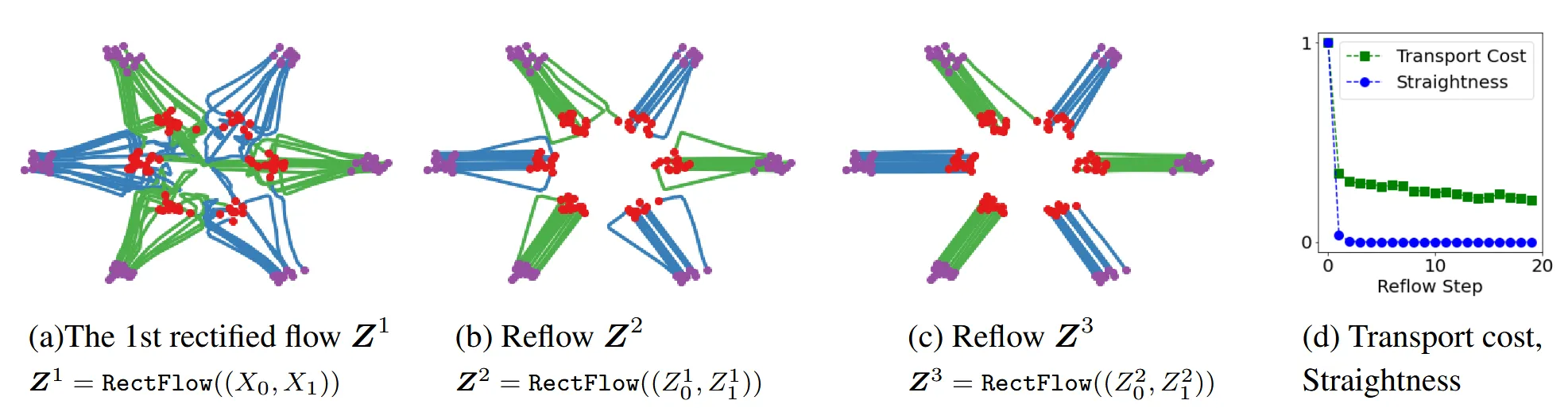
그림에서 보이는 것처럼 (a) → (b) → (c)로 rectified flow를 진행할수록 점점더 직선에 가까워지고 계산비용이 감소하는 것을 알 수 있습니다. (d) 사진을 보면 reflow step의 횟수에 따른 직진성과 비용을 나타낸 것인데, k가 커질수록 두 요소 모두 감소하고 특히 직진성은 0으로 수렴하는 것을 알 수 있습니다.

추가적으로 (d)그림에서 Reflow step이 첫번째에 기하급수적으로 감소하는데, 이는 첫번째 과정에서 교차를 최소화하는 과정에서 직선적인 형태로 많이 바뀌기때문입니다.

만약 정확한 직선 경로를 학습한다면 단일 Euler Step으로도 정확한 결과를 계산할 수 있습니다. $Z_1 = Z_0 + v(Z_0,0)$을 정확히 계산할 수 있으므로 $Z_0$으로 부터 정확한 $Z_1$을 구할 수 있습니다.

하지만 정확한 직선을 만들기는 쉽지 않습니다. 정확한 직선을 만들기 위해서는 v가 inviscid Burgers의 방정식을 만족해야 합니다. $∂_tv + (∂_zv)v = 0$

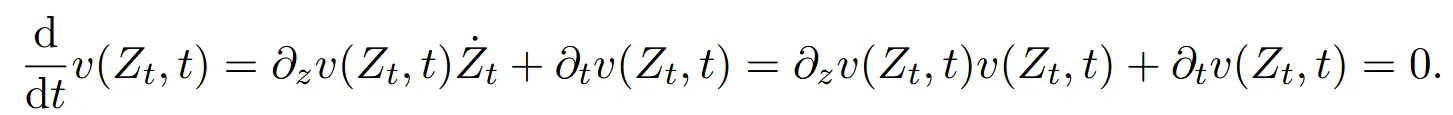
inviscid Burgers의 방정식을 더 자세히 나타내면 위의 수식과 같습니다. 더 일반적인 수식으로 나타내면 아래와 같습니다.

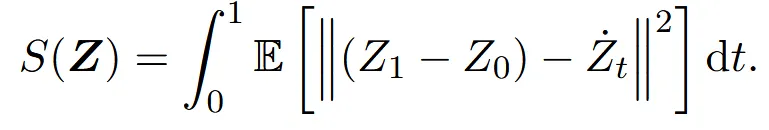
S(Z)는 주어진 경로 Z가 얼마나 직선에 가까운지를 측정하는 함수입니다. 0에 가까울수록 완전한 직선임을 의미합니다. rectification 과정을 반복할수록 S(Z)값은 0으로 수렴할 것 입니다.

개인적인 의문: 왜 직선거리를 구하기 어려운가?

→ 직선 경로를 구한다는 것은 모든 지점에서 동일한 속도로 이동해야 함을 의미합니다. 하지만 실제 데이터 분포에서 시간과 공간에 대한 속도는 동일하지 않습니다. 일반적으로 데이터 분포는 비선형적이고, 복잡한 형태를 갖습니다. 또한 각 지점에서 다른 데이터 포인트와의 상호작용도 고려해야하기때문에 결론적으로 모든 지점에서 동일한 속도를 나타내는 직선거리를 구하기 어렵습니다.

Distillation

K번째 rectifcation 과정을 반복한 모델을 얻은 후에 추론 속도를 더 빠르게 개선하기 위해 한 단계로 단순화하여 직접 예측하는 네트워크를 만드는 것입니다.

K번의 rectification 과정을 거친 모델은 거의 직선에 가깝다고 가정을 하면 distillation 과정이 더 효율적으로 작동합니다.

Distillation 즉, K번의 rectification한 모델을 학습하는 모델을 $\hat{T}$라고 하면 수식은 위와 같고, Loss식은 아래와 같습니다.

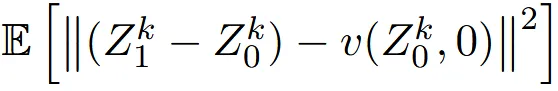
On the velocity field $v^X$

만약 $X_1$을 알고 있을 때 $X_0$의 확률 밀도를 알고 있으면, 즉 조건부 밀도 함수($p(x_0|x_1)$)를 알고 있으면, $v^X$는 아래와 같이 표현할 수 있습니다.

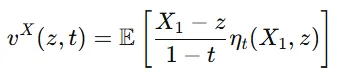
여기서 $η_t(X_1,z)$는 아래와 같이 정의됩니다.

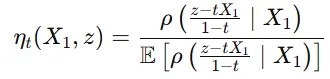
첫번째 수식은 특정 시간 t에서 점 z가 주어졌을 때, 그 점이 어떤 방향으로 이동해야 하는지를 정의합니다.

두번째 수식은 조건부 확률 밀도 함수의 비율을 의미하며, 데이터가 특정 조건을 만족하는지 여부에 따라 가중치를 부여합니다. 쉽게 말하면 현재 위치 z에서 목표 위치 $X_1$ 로 이동할 때 어떤 방향으로, 어떤 가능성을 가지며 이동할지를 수치화한 확률적인 지침입니다.

$v^X$는 현재 위치에서 목표 상태로 이동할 때, 해당 경로가 가장 가능성 있는 경로가 되도록 하기 위해 조건부 밀도 함수를 사용하여 비율을 조정합니다.

1. 조건부 밀도 함수(p)가 양수이고 모든 곳에서 연속일 경우 $v^X$도 모든 시공간에서 잘 정의되고 연속적이라는 것을 의미합니다.
2. $logη_t$가 z에 대해 연속적으로 미분 가능하다는 것은 $η_t$의 변화가 부드럽게 이루어지며 갑작스러운 변화 없이 잘 정의된다는 의미입니다. 이경우 아래 수식이 성립합니다.

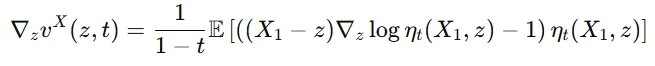
1. $v^X$가 모든 구간 [0,a], a<1 구간에서 일정한 Lipschitz 연속성을 만족한다면 ODE는 유일한 해를 가질 수 있습니다.

만약 조건부 밀도 함수를 알지 못할 경우 $v^X$는 정의할수 없거나 불연속적입니다. 이를 해결하기 위해서 가우시안 노이즈를 $X_0$에 추가하여 새로운 변수를 만들고 변환된 변수를 사용하여 변환합니다.

Smooth function approximation

이전에 설명한 조건부 확률 밀도를 이용해서 $v^X$를 구하는 방법은 데이터를 너무 잘 맞춰서 과적합하게 됩니다. 따라서 neural network 또는 non-parametric 모델과 같은 방법을 사용합니다.

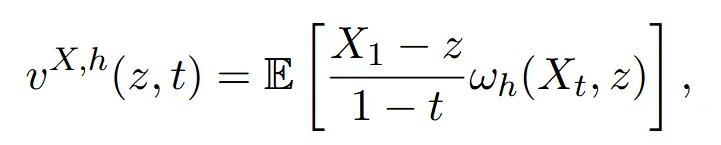
저차원 문제의 경우 Nadaraya-Waston style(위의 수식)을 사용해서 조건부 확률 밀도를 알지 못해도 대략적인 $v^X$를 생성할 수 있도록 합니다.

실제로 사용할 때는 위의 기댓값(E) 대신에 empirical averaging(경험적 평균)을 이용합니다. 경험적 평균은 기댓값과 달리 무한한 경우가 아닌 실제로 얻은 유한한 샘플의 결과의 평균입니다.

A Nonlinear Extension

일반적으로 Linear interpolation 방식이 성능이 더 좋다는 것을 보여주는 부분이므로 필수적인 부분은 아닙니다.

기존에 linear interpolation으로 나타낸 $X_t$를 $X_0$와 $X_1$의 time-differentiable curve로 변경함으로써 Nonlinear한 방법으로 나타낼 수 있는 방법을 설명합니다.

직선 경로(최단 경로)를 Nonlinear하게 변경함에 따라 Transport Cost는 더 커질 것입니다.

Probability flows나 DDIM이 해당 방법의 특별한 경우라고 볼 수 있습니다.

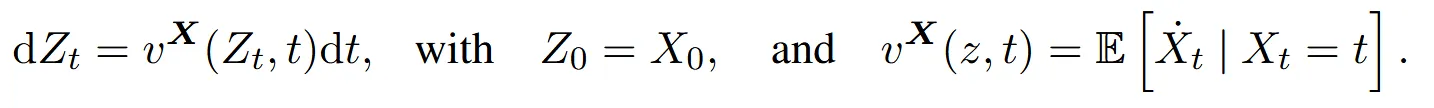
위의 수식에서 $\dot{X}_t$는 $X_t$의 시간 변화량을 나타냅니다. $v^X$를 풀기 위해 아래의 식을 보면

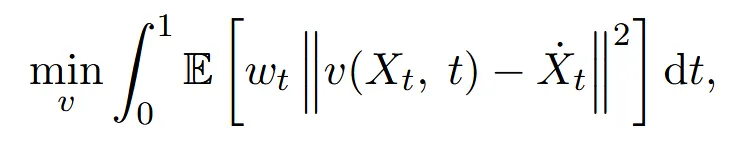
t시점에서 기대되는 속도 v와 실제 시간 변화율 간의 차이를 최소화하는 것을 목표로 합니다.

Probability Flow ODEs and DDIM

Probability flow ODEs(PF-ODEs) 모델과 denoising diffusion implicit models(DDIM) 모델은 모두 Probability flow를 사용하여 SDE를 ODE로 변환하는 과정입니다.

PF-ODE 모델들은 여러 변형들로부터 유도됩니다. 더 자세한 사항은 해당 논문 참고

• Variance-Exploding(VE) SDE: 분산이 점점 증가하는 형태의 SDE
• Variance-Preserving (VP) SDE: 분산이 일정하게 유지되는 SDE
  • DDIM의 continous time limit과 동일
• Sub-VP SDE: VP보다 낮은 분산을 가지는 SDE

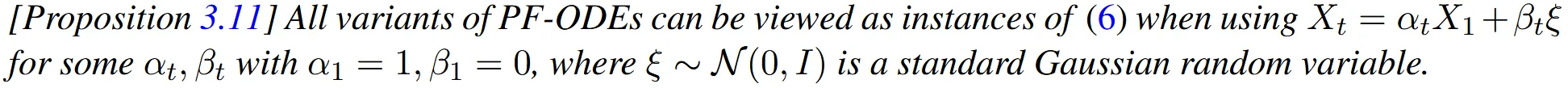
PF-ODEs는 $X_t = atX1 + Btξ$의 형태로 나타낼 수 있습니다. 기존 interpolation과 다르게 확률적 특성을 유지하면서 자연스러운 이동을 요구하기 때문에 반드시 t=0일 때 a1=1이고 B1=0일 필요는 없습니다. 하지만 시작 지점을 명확하게 정의하기 위해서 X0대신 표준 가우시안 랜덤 변수인 ξ를 도입하게 됩니다.

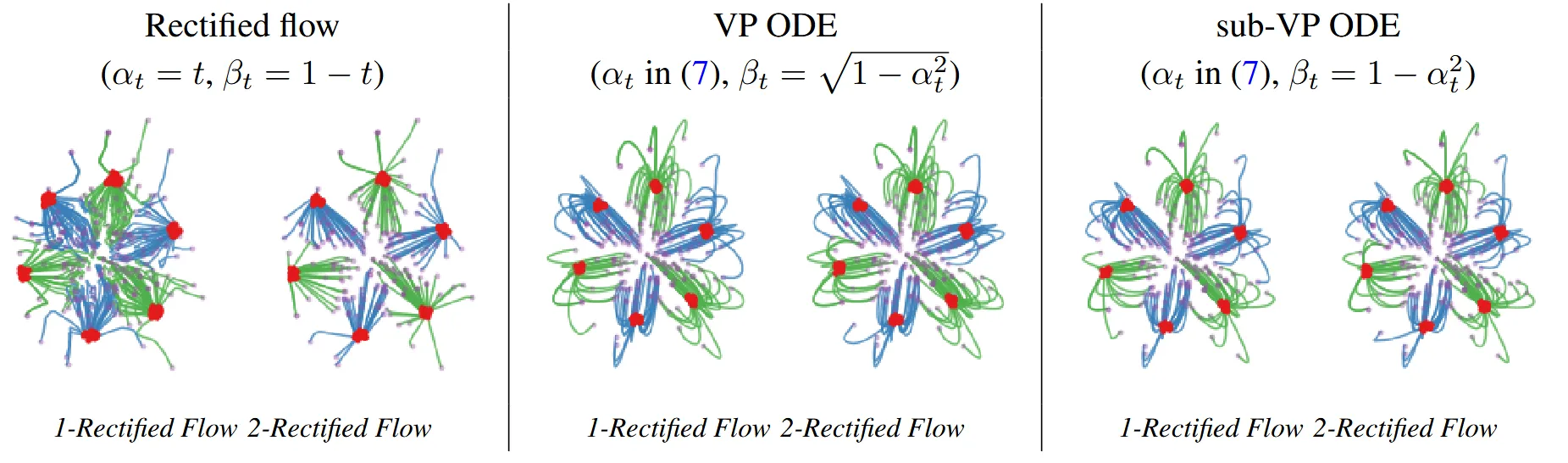
해당 그림은 Recitified flow(맨왼쪽)과 VP ODE(가운데) 그리고 sub-VP ODE(맨오른쪽)의 결과를 비교한 그림입니다. Rectified flow는 데이터의 분포의 이동에서 거의 직선형태를 보이지만, 나머지 2개의 경우 이전에 설명했던 것처럼 경로가 더 길어진 곡선형태인 것을 확인할 수 있습니다.

VP ODE and sub-VP ODE

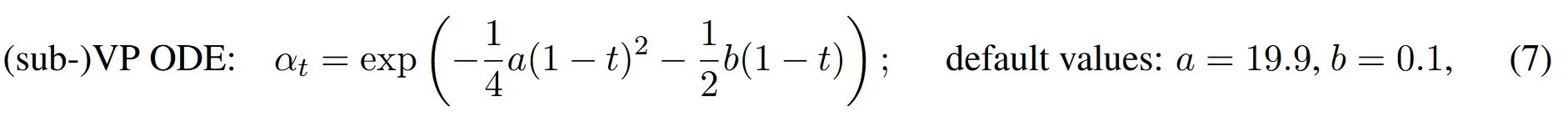
VP ODE와 sub-VP ODE는 $a_t$를 공유하면서 사용합니다.

이후 $B_t$의 값은 위의 수식처럼 서로 다르게 사용합니다. $B_0$이 1에 가까울 때 2모델 모두 데이터의 분포는 가우시안 정규분포를 따릅니다. 위에 보이는 것처럼 $B_t$를 잡았기 때문에 직선적이지 않는 경로를 가집니다. 직선적인 경로를 만들기 위해서는 $B_t = 1 - a_t$로 설정해야합니다.

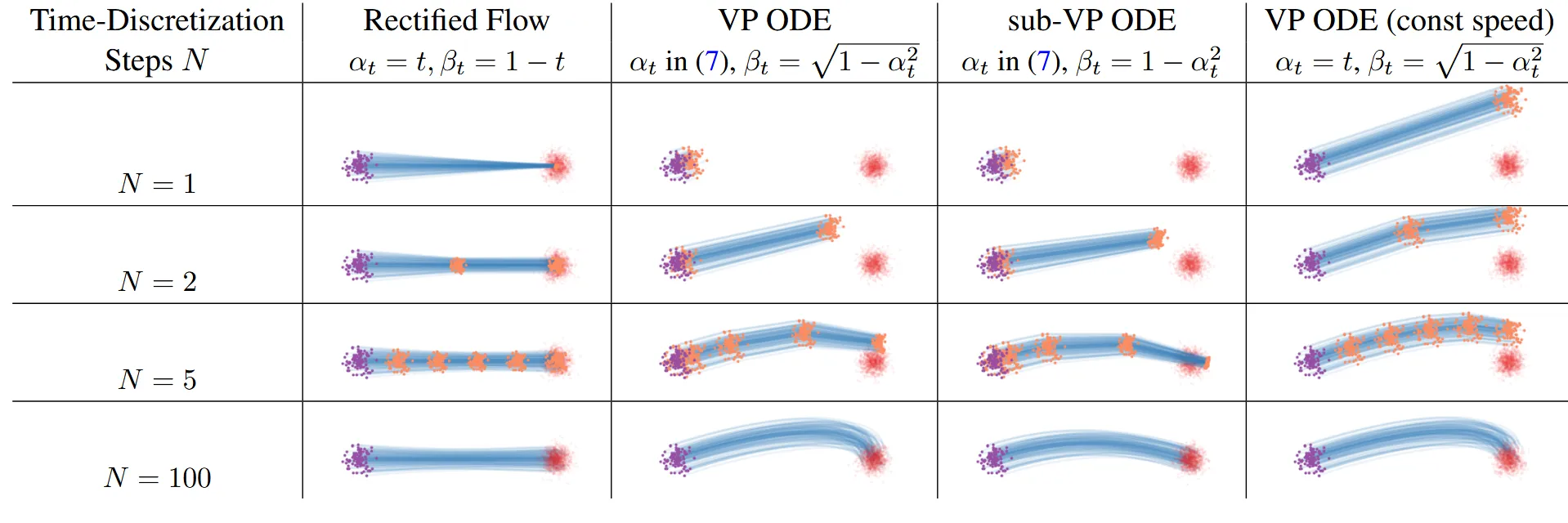
해당그림에서 보라색 점들은 $π_0$을, 빨간색 점들은 $π_1$을, 주황색 점들은 중간단계를, 파란색 곡선은 flow 궤적을 나타냅니다. Rectified flow의 경우 모든 시간간격이 균일하고 하나의 직선 경로를 나타내기 때문에 N=2인 경우에도 충분히 좋은 결과를 얻을 수 있습니다.

이에 반해 나머지 모델들은 초반에 느리고 후반에 빨라지는 것을 볼 수 있습니다. 또한 직선경로가 아닌 것을 볼 수 있습니다. 그리고 Rectified Flow 모델과는 다르게 N=2만으로는 충분한 결과를 도출할 수 없고, 더 많은 steps가 필요한 것을 시각적으로 확인할 수 있습니다.

마지막 열에서 $a_t$를 y로 지정하면서 균일한 업데이트 속도를 얻을 수 있습니다.

VE ODE

$a_t=1$, $B_t = σ_{min}\sqrt{r^2(1-t)-1}$ 로 값을 지정해서 학습을 하는 과정입니다. 즉 t=0인 시점에서 분산이 매우크기 때문에 위의 2가지 그림 예시에서 제외했습니다.

Summarize

Nonlinear Rectified Flow의 이점은 아래와 같습니다.

1. ODE 학습을 SDE 방법 없이 직접 독립적으로 고려할 수 있습니다.
2. 학습된 ODE의 경로를 어떤 매끄러운 interpolation 곡선으로 지정할 수 있습니다.
3. 초기 분포를 interpolation 경로와 독립적으로 임의로 선택할 수 있습니다.
4. 기본 interpolation 방식으로 $X_t = tX_1 + (1-t)X_0$라는 linear interpolation을 추천합니다.

Code 구현 결과

링크: https://colab.research.google.com/drive/1CyUP5xbA3pjH55HDWOA8vRgk2EEyEl_P?usp=sharing
해당 링크에 코드 구현에 대해서 자세히 나타나있어서 한번 실행시키면서 따라가면 이해에 도움이 될거같습니다.

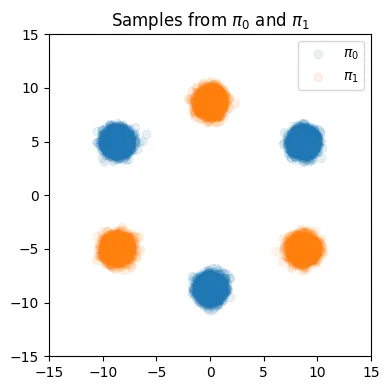
3개의 컴포넌트에 대해서 평균값에 차이를 준 2개의 데이터 분포를 시각화합니다.

학습과정은 MLP를 이용해서 했으며, 자세한 내용은 링크를 통해서 확인할 수 있습니다.

100번의 Step을 한 결과입니다.

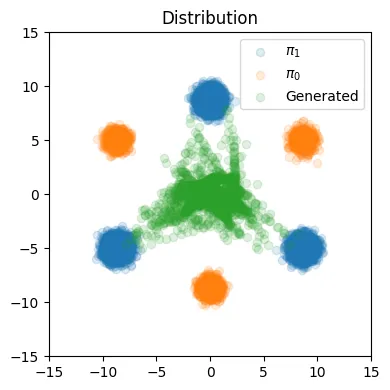
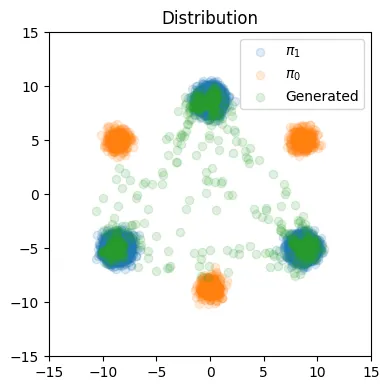
주황색이 초기분포, 파란색이 목표 분포로서 위에서 봤던 사진이었고, 초록색 점들은 Rectified flow를 한번 학습 했을 때 나온 모델의 분포입니다. 이상한 부분들이 조금은 존재하지만 대부분 파란색 점 즉 우리의 목표 분포로 잘 이동한 것을 확인할 수 있습니다.

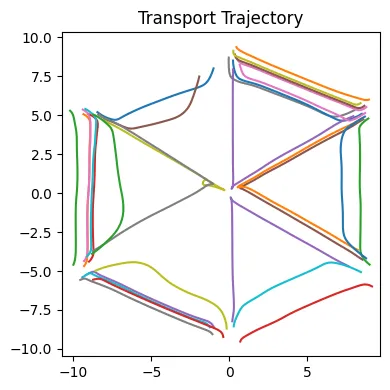
위의 사진은 초기 분포에서 목표분포로 이동하는 각 데이터의 포인트의 경로를 나타낸 것입니다. 완벽한 직선 형태는 아니지만 대부분 직선의 형태로 잘 이동하는 것을 확인할 수 있습니다. 가운데로 향하는 몇개의 직선들은 반대편의 분포로 향하다가 끝까지 안가서 학습이 완전하게 이루어지지 않은 것으로 추정할 수 있습니다.

1개의 Step만 한 경우 데이터가 효율적으로 이동하지 않은 것을 알 수 있습니다.

이제 2번의 rectified flow를 학습해서 결과의 비교를 해보도록 하겠습니다.

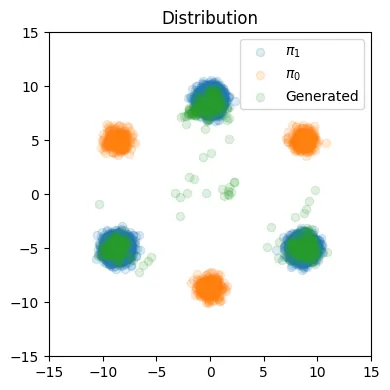
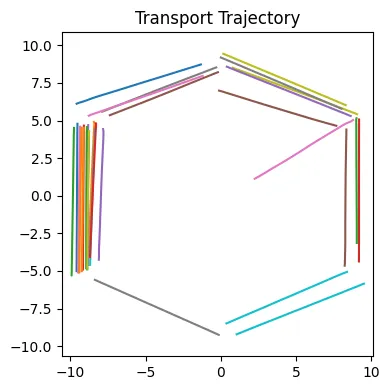
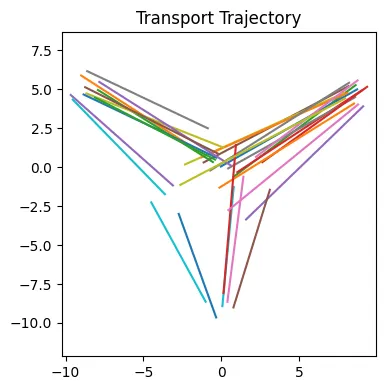
Euler step이 100인경우 위의 그림과 같은 결과가 나왔습니다.

경로도 이전에 비해서 가운데로 가는 비율이 줄었고, 훨씬 더 직선에 가까운 형태를 나타내고 있습니다.

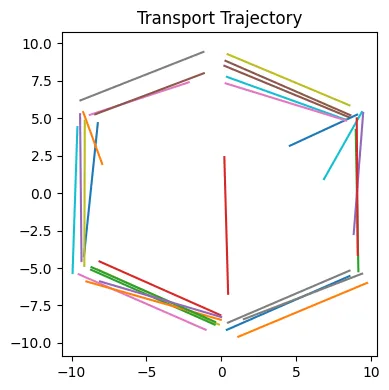
Euler step이 1인 경우도 성능이 개선된 것을 확인할 수 있습니다.