FlowEdit: Inversion-Free Text-Based Editing Using Pre-Trained Flow Models [2025 ICCV]

이한결·2025년 7월 14일

원본 이미지에서 일부를 수정하기 위해서 T2I(Text to Image)모델들에서는 Inversion을 진행합니다. 하지만 Inversion만으로는 만족스러운 결과를 얻지 못해서 추가적인 sampling 방식들을 사용했습니다. 이러한 추가적인 방식들을 통해서 성능을 높일 수 있지만, 특정 모델에 특화된 방식이다 보니 새로운 모델에 적용하기 어렵다는 단점이 존재했습니다.

FlowEdit 모델은 이러한 한계를 극복하기 위해서 inversion과 optimization 방법을 사용하지 않고 특정 모델에만 특화 되지 않은 새로운 방법을 제시했습니다. Inversion을 통해서 노이즈를 더했다가 변환하는 것이 아니라 원본 이미지에서 바로 목표로 하는 경로로 이동하는 방식입니다. FlowEdit을 사용할 경우 transport cost가 낮아져서 원본 이미지를 더 잘 보존하면서 이미지 수정이 가능해집니다. 이제 어떻게 FlowEdit이 이를 가능하게 했는지 확인해보도록 하겠습니다.

Preliminaries

Rectified Flow models

Generative Flow 모델은 $X_0$ 과 $X_1$ 이라는 두 확률분포 사이를 연결해주는 경로를 만들어주는 모델입니다.

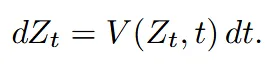
위의 식은 시간 t에 따라 V라는 vector field가 조금씩 변화하는 의미입니다. 보통 $X_1$ 을 gaussian distribution으로 잡고 우리가 원하는 이미지의 분포를 $X_0$ 로 잡습니다.

Rectified flows는 주로 위와 같이 linear interpolation 방식을 사용해서 경로를 만들기 때문에 적은 step으로도 빠른 결과를 생성할 수 있습니다.

Text-to-Image Flow model은 text prompt C를 condition으로 받아서 vector field를 예측합니다.

Image editing using ODE inversion

입력된 이미지 $X^{src}$ 와 텍스트 $c_{src}$ 이 있을 때 이를 target 텍스트 $c_{tar}$ 를 기반으로 우리가 수정하고자 하는 이미지 $X^{tar}$ 로 바꾸기 위한 과정을 진행하기 위해서 ODE inversion을 진행합니다.

우선 입력된 이미지를 다시 t=1 시점으로 보내기 위한 inversion 과정을 진행합니다. 위의 수식과 타이 t=0인 시점의 이미지는 텍스트(t, $C_{src}$ )를 기반으로 t=1인시점의 분포로 변환됩니다.

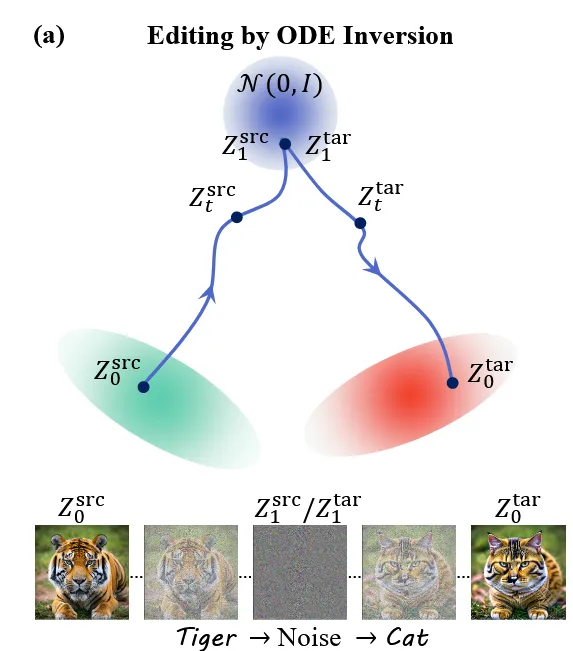
이 과정을 그림으로 나타내면 위와 같습니다. 왼쪽 아래의 그림이 입력 이미지이고, 이를 t=1인 시점으로 inversion을 한 것입니다.

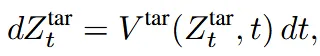
이후 위의 그림에서 빨간색 우리가 원하는 분포로 가기 위해서 다시 $c_{tar}$ 를 기반으로 backward를 진행하는 것입니다. 하지만 위의 그림에서도 보이는 것처럼 우리가 원하는 퀄리티의 결과는 나오지 않습니다.

이러한 결과를 보완하기 위해서 inversion 과정에서 feature map을 추가하는 트릭도 사용했지만, 이는 특정한 모델에 특화된 방식입니다.

Reinterpretation of editing by inversion

이미지를 바꾸기 위해서 Inversion을 통해서 noise한 분포에서 다시 backward 하는게 아닌, 이미지 분포에서 우리가 원하는 타겟 분포로 바로 변환하는 방법을 새롭게 제안했습니다.

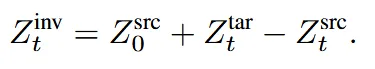
$Z_t^{inv}$ 라는 분포를 위의 수식과 같이 제안 했을 때, t=1인 경우 마지막 2개의 항이 가우시안으로 제거 돼서 원본 이미지가 되고, t=0인 경우 target 이미지가 됩니다. 즉 1 → 0 으로 갈수록 원본 이미지에서 점점 타겟 이미지로 변형 되는 분포가 된 것입니다!

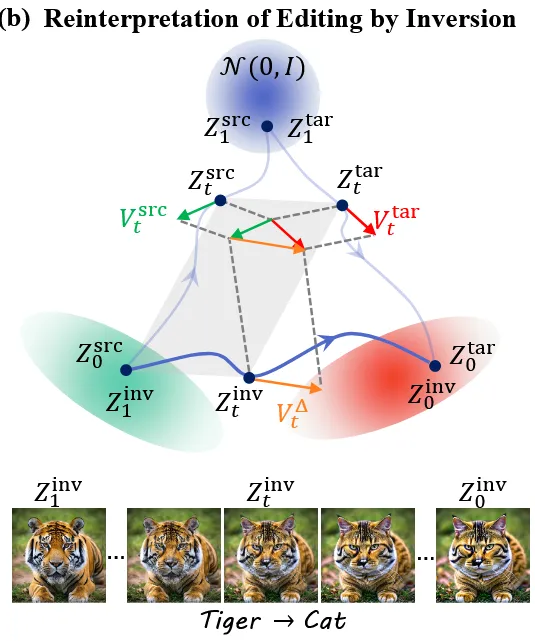
이 과정을 그림으로 나타내면 위와 같습니다. 회색 평행사변형이 방금 설명한 inversion path를 설명하는 부분입니다. $Z_0^{src}$ 에서 시작해서 target vector field(빨간색 화살표)와 source vector field(초록색 화살표)의 차이(노란색 화살표)로 이동하는 것을 알 수 있습니다.

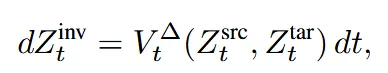
방금 화살표의 차이만큼 이동한다를 수식으로 나타낸게 위와 같습니다.

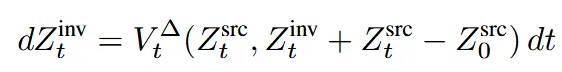
최종적으로 이전 수식에서 $Z_t^{tar}$ 을 그림 위의 수식에서 얻어서 대입하면 위와 같은 수식으로 source에 관한 수식이 나와게 됩니다.(그냥 $Z_t^{tar}$ 남기고 다 이항한다음에 값 대입! 절대 어려운 개념 아님!!)

이렇게 정의한 path의 특징은 noise-free하다는 점입니다. 그림을 기반으로 설명드리자면 2개의 화살표에는 동일한 t시점의 노이즈 성분과 vector field 값이 있는데 동일한 노이즈 성분은 동일하기 때문에 제거하면 0이므로 noise-free 하다는 것입니다.

Vector field 변화측면을 자세히 살펴보면 t=1과 가까운 시점에서 $Z_t^{tar}$ 와 $Z_t^{src}$ 는 모두 노이즈가 많이 있는 상태로서 2개의 차이를 제거하면 coarse한 값들의 차이가 나올 것이고, t=0과 가까운 시점에서 제거하면 fine한 값들의 차이가 나올 것입니다. 따라서 어느 시점에서 차이를 주냐에 따라서 coarse-to-fine editing이 가능하게 됩니다.

FlowEdit

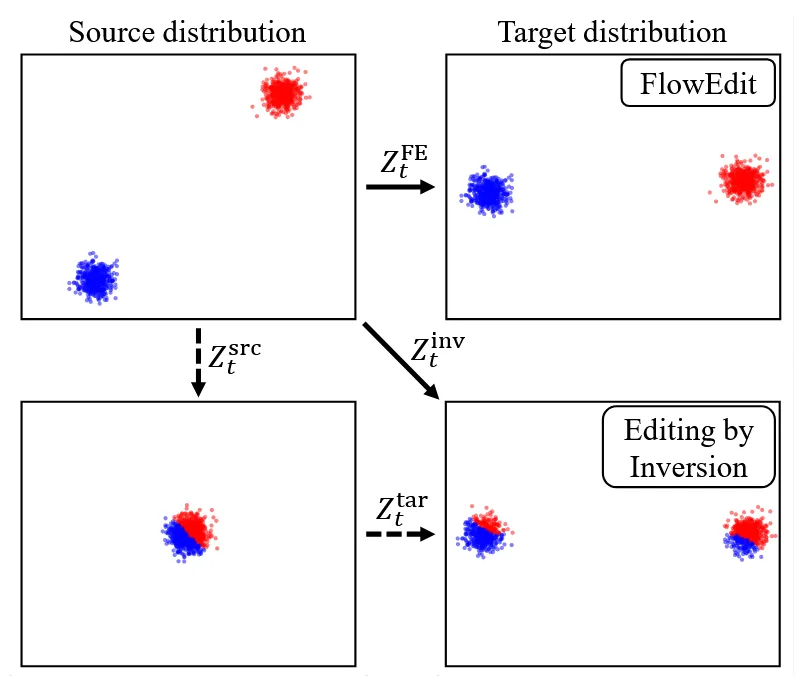
Inversion을 통해서 이미지를 변화시킬 수 있는 것은 맞지만, 우리가 원하는 형태로 변환되는 것은 아닙니다. 위의 그림에서 왼쪽 아래의 그림처럼 2개의 분포를 모두 가우시안 혼합 분포로 두고 inversion을 통해서 이미지 변환을 진행할 경우 오른쪽 아래처럼 엉뚱하게 연결되는 것을 알 수 있습니다. 이는 초기 노이즈로 매핑 되는 과정에서 샘플의 상대적 위치가 그림의 왼쪽 아래처럼 왜곡 되기 때문입니다.

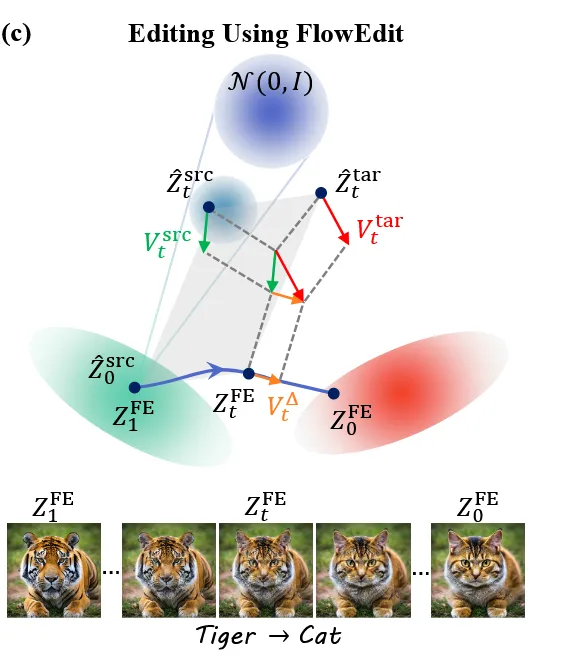
FlowEdit을 사용하면 노이즈를 평균해서 상쇄 하기 때문에 최소 경로로(low transport cost) target distribution으로 변환이 가능합니다. 최소 경로기 때문에 target distribution 중에서 가장 가까운 부분을 선택하게 됩니다. 하지만 transport cost가 작기 때문에 원본이 잘 보존되고, heursitic 한 방법이지만 가장 높은 성능을 달성했습니다.

그러면 A에서 B분포로 갈 때 어떤 경로를 따라야되는지 설명하도록 하겠습니다. A에서 B로 갈 때 각 timestep t에서 각각의 velocity field가 존재하고, 이를 전부 평균 낸 경로를 선택해서 이동하도록 해서 전체적으로 가장 덜 꼬이고, 덜 변형되는 편집이 되도록 합니다.

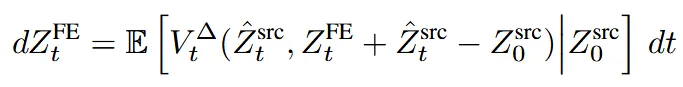
이를 수식으로 나타낸 것이 위와 같습니다. FE(FlowEdit)는 (1,0)범위에서 여러 t에 대해서 velocity field를 구하고 이를 평균(E[])낸 값을 사용하는 것입니다.

Practical considerations

실제로 사용할 때는 discrete한 time을 평균 내어서 FlowEdit를 예측합니다. 사용할 t의 개수를 $n_{avg}$ 라는 파라미터를 이용해서 정할 수 있습니다. 해당 값이 작을수록 부정확하고, 많을수록 더 정확한 값을 얻을 수 있습니다.

만약 노이즈가 서로 영향을 준다면 결과가 불안정해질 수 있으므로 $E[N_tN_s]=0$ 식처럼 2개의 노이즈는 independent 하게 작동하도록 합니다.

또한 기존 inversion 수식처럼 처음 몇개의 step은 skip 할수 있도록 설정하는 파라미터 $n_{max}$ 를 사용합니다. Inversion에서는 아마 starttimestep? 이런 변수로 지정할 수 있는데 여기서는 시작을 $T - n{max}$에서 하도록 설정할 수 있습니다.

위에서 설명한 전체적인 FlowEdit의 알고리즘은 위와 같습니다. 시작은 for문에서도 보이는 것처럼 $n_max$ 에서 시작해서 timestep 0 까지 진행합니다. 각 for문이 진행될 때 총 $n_{avg}$ 의 값을 평균한 FlowEdit을 사용해서 경로를 따라 이동합니다.

Comparison to editing by (exact) inversion

FlowEdit이 transport cost가 inversion transport cost보다 작다는 것을 증명하는 부분입니다.

초기 noise를 정확히 아는 Synthetic image(real image의 초기 latent는 추정값이지 정확한 값이 아니므로) 1000개를 활용해서 a photo of cat에서 cat을 dog로만 변환하는 과정을 진행합니다. 결과를 비교하기 위해서 source latent와 target latent와의 MSE와 LPIPS를 측정합니다. 그 결과 1376 vs. 2239 for MSE, 0.15 vs. 0.25 for LPIPS로 2개 모두 FlowEdit이 압도적으로 작은 것을 알 수 있습니다.

이번에는 SD3 모델로 만든 강아지 사진과, FlowEdit와 Inversion 각각을 Cat → Dog로 변환한 이미지에 대해서 FID와 KID 값을 비교해서 얼마나 잘 변형했는지 확인했습니다. 그 결과 FID 51.14 vs. 55.88 KID 0.017 vs. 0.023로 FlowEdit가 더 잘 변형한 것을 알 수 있습니다.