GAN논문 링크
Generative Model
데이터의 확률 분포를 학습하여 새로운 데이터를 생성하는 모델
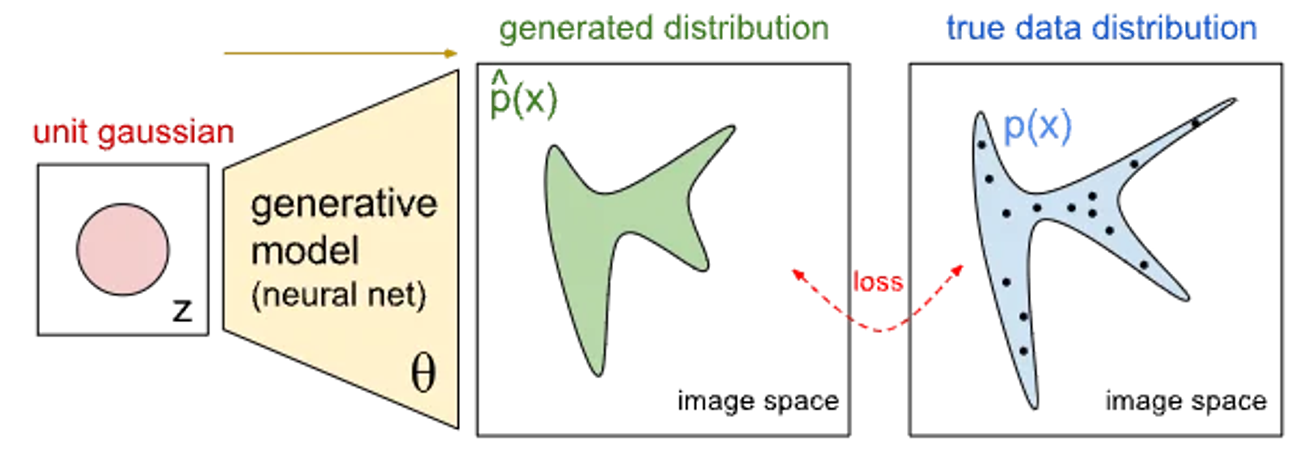
오른쪽 파란색의 true data 즉 주어진 데이터 셋의 특징을 학습해서, 초록색 우리가 원하는 새로운 데이터를 만들어내는 모델이다.
생성 모델은 확률적 모델과 신경망 기반 모델이 존재한다
확률적 모델
데이터가 특정한 확률 분포를 따른다고 가정하고, 해당 분포를 추정하여 새로운 데이터를 생성
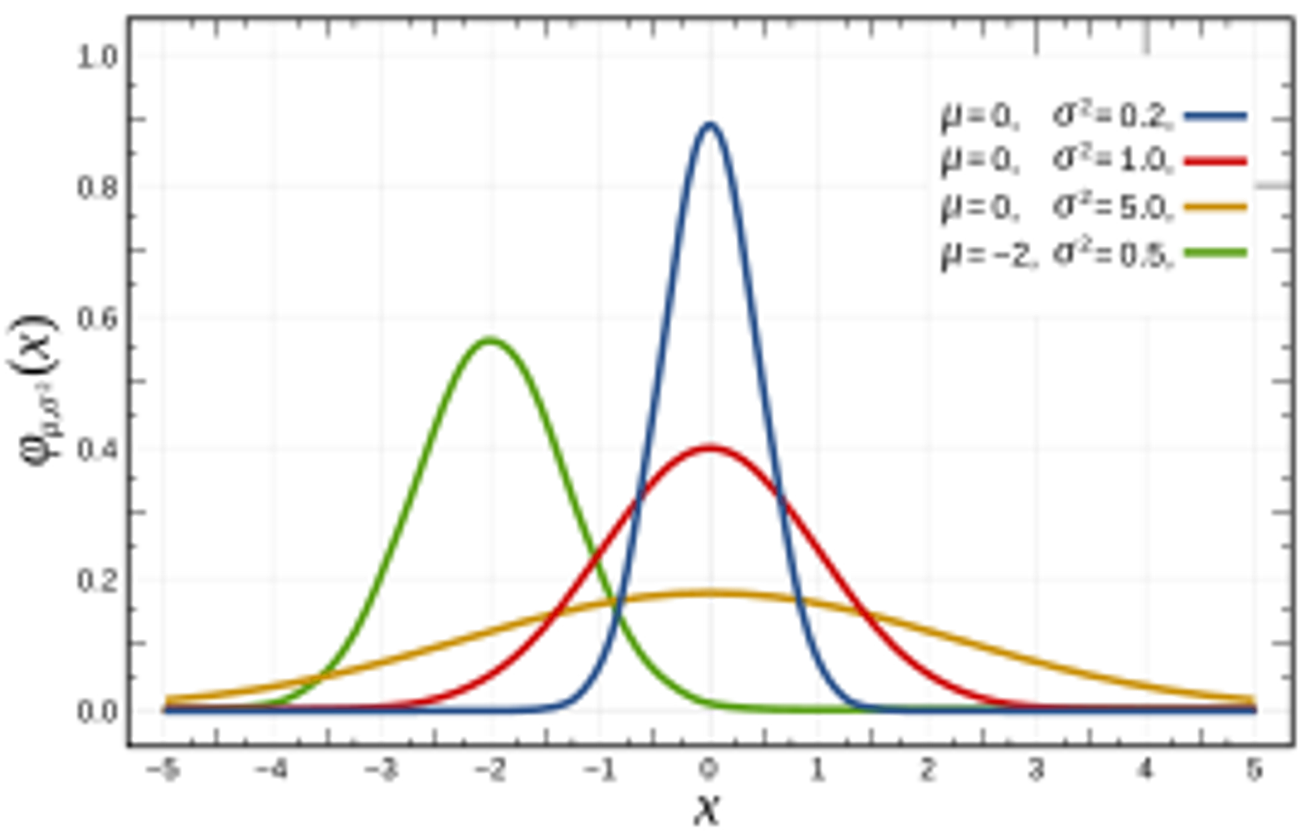
사람들의 키에 대한 분포를 그린다면 해당 분포는 정규분포를 따를것이다. 예시로는 키를 들었지만 세상의 다양한 데이터들을 많이 모아서 해당 분포를 그린다면 아마도 정규분포를 따를 가능성이 높다. 이처럼 데이터들이 정규분포 혹은 특정한 확률 분포를 다른다고 가정하고, 해당 분포를 추정해서 새로운 모델을 만드는 방법이다.
Ex: GMM(Gaussian Mixture Models), HMM(Hidden Markov Models)
신경망 기반 모델
딥러닝 기술을 활용하여 데이터 분포를 학습하고 새로운 데이터를 생성
EX: GAN(Generative Adversarial Networks), VAE(Variational Autoencoder)
Discriminator vs Generator
Discriminator(판별자)
CNN을 접해신 분들이라면 Classification(분류) 모델에 대해서 한번쯤 들어봤을 것이다. 해당 모델처럼 어떤 입력(여기서는 가짜와, 진짜 이미지)에 대해서 분류 해주는 역할을 한다
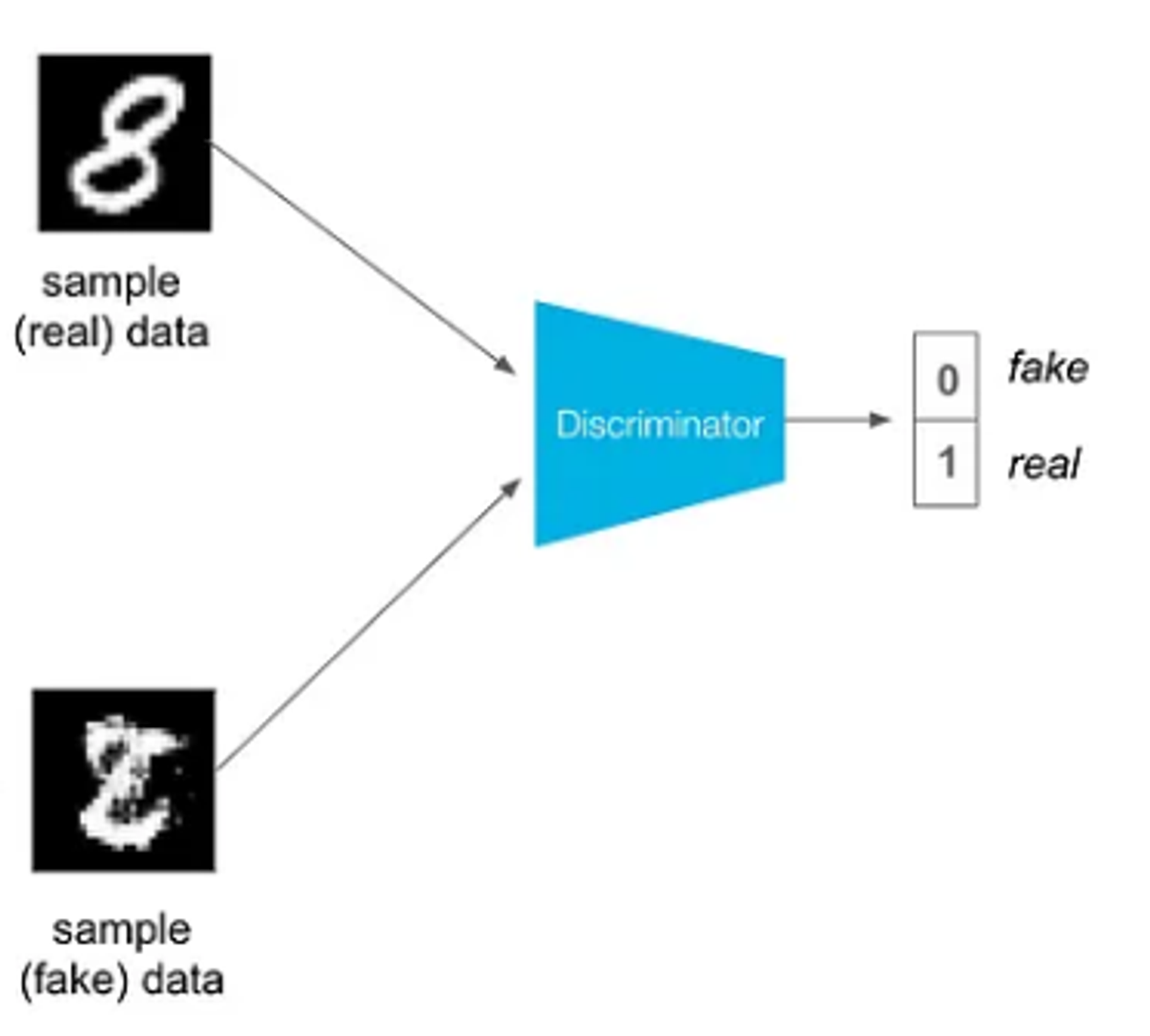
위의 진짜 숫자 8, 우리가 만든 가짜 숫자 8을 Discriminator를 통해서 분류하는 작업을 진행한다. Classification model은 multilayer perceptron을 이용했다.
Generator(생성자)
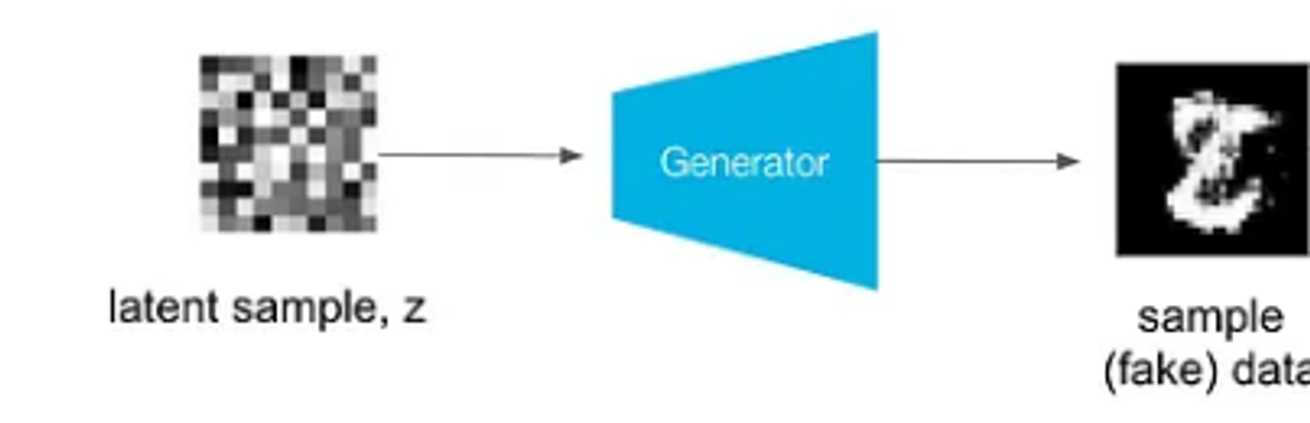
가짜 숫자를 만드는 역할을 Generator가 한다. 여기서 어떤 입력값을 넣어서 어떻게 가짜 이미지를 생성할 수 있을까? 아래에서 자세히 이야기하겠지만 지금은 어떤 임의의값이라고 생각하자(노이즈). 어떻게 생성하는지는 우리가 Classification에서 많이 봤던 multilayer perceptron이다. 파란색 부분이 이에 해당한다.
가우시안 분포(Gaussian distribution)
생성 모델을 보면 가우시안 분포의 값이 들어간다고 나온 걸 들은적이 있을것이다. 이번기회에 이 가우시안 분포에 대해서 확실하게 정리하고 지나가겠다. 가우시안 분포는 정규분포라고도 분리며 특정한 평균과 분산을 갖는 데이터를 모델링하는데 사용된다
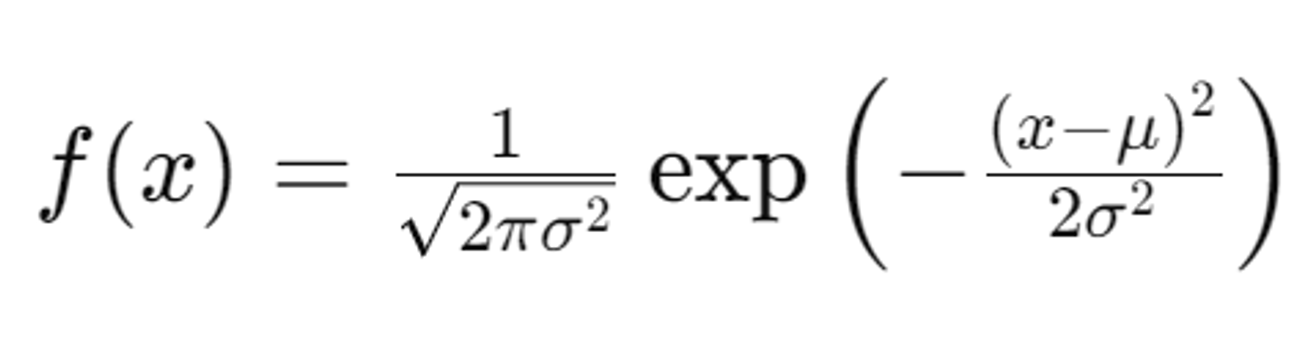
μ: 평균 / σ: 표준편차 / σ^2: 분산
가우시안 분포의 특징
- 정규성: 종 모양의 대칭적인 곡선 형태(평균을 중심으로 대칭)
- 분포의 위치는 평균에 의해, 분포의 폭은 표준편차에 의해 결정
GAN에서는 생성자가 latent space에서 샘플을 생성하는데, 이 latent space는 종종 가우시안 분포로부터 샘플링된 값을 사용
이유? 가우시안 분포의 특성 덕분에 생성자가 학습하는 동안 다양한 입력값에 대해 고르게 잘 작동하도록 돕기 때문
한마디로 다양한 패턴과 특징을 효과적으로 학습하기 위해!
minmax game
GAN 모델을 설명할 때 항상 나오는 사진은 경찰과 도둑이다. 논문에서도 이와같은 설명을 진행했다. Generator는 위조지폐를 만드는 도둑, Discriminator는 이런 위조지폐를 판단하는 경찰이다. 도둑은 경찰에게 들기지 않게 최선을 다해서 실제 돈과 비슷하게 만들것이고, 이런 가짜 돈을 경찰은 최선을 다해서 구분할것이다.
GAN의 장점
No approximate inference or Markov chains are necessary
→ 우리는 근사추론이나 마르코프 연쇄를 사용하지 않아서 간단하고 효율적이야! 라고 논문은 주장을 하고 있다. 해당 내용에대해서는 논문에 자세히 나오지않아 간단한가보다 생각하고 넘어갔다.
Network 구조

이식을 보면 이전에 나왔던 minmax게임이라는 말이 왜 나왔는지 알 수 있을 것이다.
Discriminator 입장: V(D,G) 최대화
D(x)의 값을 1로, D(G(z))의 값을 0으로 한다면 V값이 0이 되어 최대화가된다.
이때 D(X)는 실제 데이터를 실제로 인식하는 확률, D(G(z))는 가짜 데이터를 실제로 인식하는 확률이다
Generator 입장: V(D,G) 최소화
D(x)의 값을 0으로 , D(G(z))의 값을 1로 한다면 V값이 최소가 될것이다.
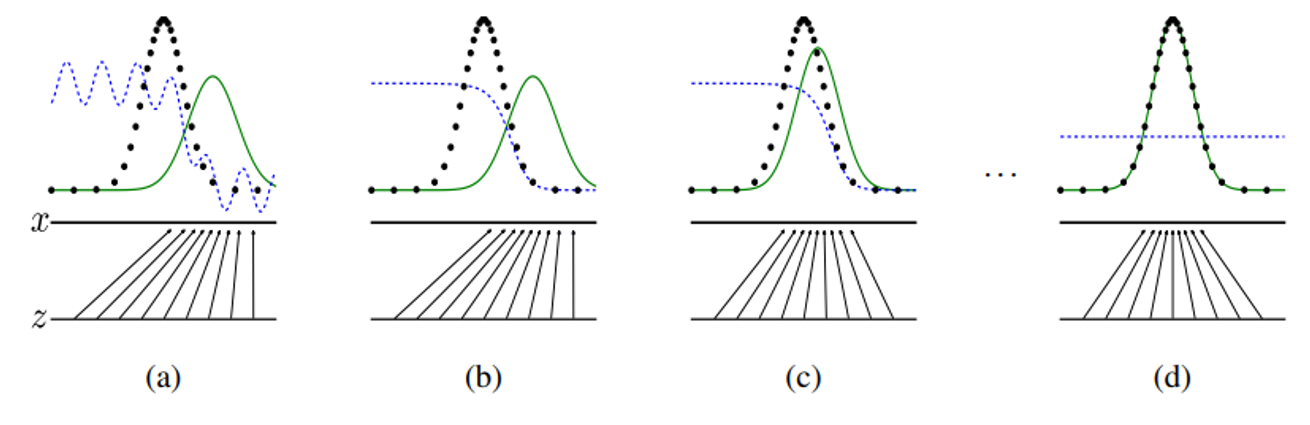
x: 데이터(실제 이미지들의 모음) // z: 입력 noise
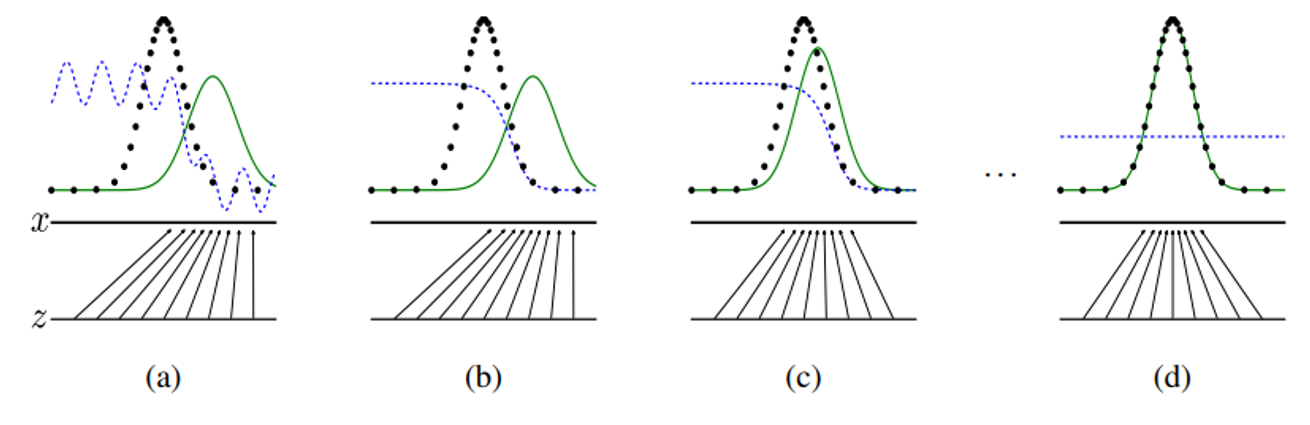
x축: 입력 공간, 랜덤하게 샘플링된 데이터 포인트
z축: latent space, 생성자 네트워크가 입력으로 사용하는 공간
검정색 점: 원본 데이터들의 분포(정규분포와 유사)
초록색 점: 생성 모델의 분포
파란색 점: 판별 모델의 분포
(a) → (b) →(c) → (d): 점점 학습이 진행되는 단계를 그림으로 나타낸다
- 초록색 점들은 점점 더 검정색 점들과 유사하게 학습이 진행된다. 즉 생성 모델의 분포는 최대한 원본 데이터들과 유사해지게 학습된다
- 위의 결과로 인해 판별자는 점점 더 실제 데이터와 생성된 데이터를 구분하지 못해 결과적으로 구분할 확률이 1/2가 된다
마치며
논문에 추가적으로 증명 부분과 Experiment 부분도 나오지만 필요한 부분만 읽고 나중에 추가적으로 해당 부분은 올려두도록하겠습니다.
