NeRF(Representing Scenes as Neural Radiance Fields for View Synthesis) 논문리뷰

https://arxiv.org/pdf/2003.08934

Introduction

NeRF는 객체의 3D 모델을 생성하는 기술이 아니라, 객체를 바라보는 모든 장면을 생성하는 View Synthesis 기술입니다.

view synthesis: 물체를 새로운 시점에서 본 영상으로 만들어주는 것

3D 모델: 장면이나 객체의 전체적인 3D 구조를 정확하게 재현하는 데 초점을 맞춘다. (SFM)

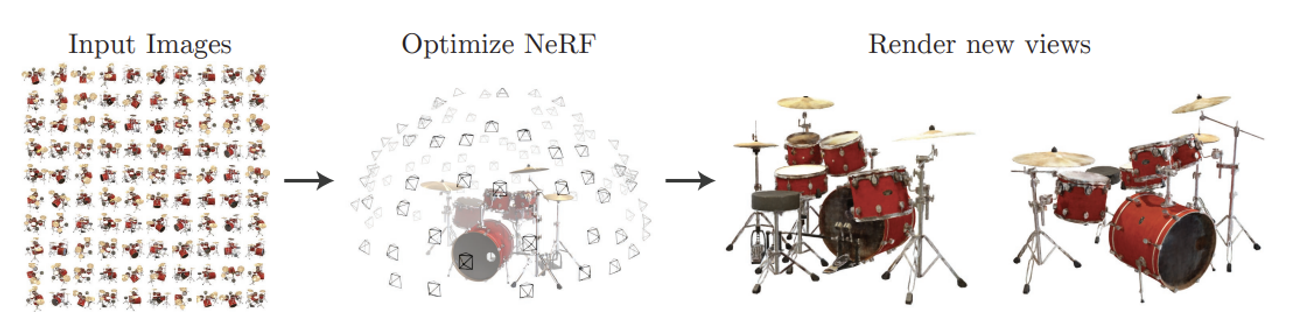
100개의 서로 다른 시점에서 찍은 이미지를 NeRF를 이용해서 학습하면, 처음 보는 시점에서 보는 드럼의 2D 이미지를 얻을 수 있습니다.

기존의 3D 모델링들은 voxel grid와 같은 많은 저장공간이 필요로 하는 데이터들을 사용했지만, NeRF의 경우 저장공간을 많이 차지하지 않는다는 장점이 있습니다.

Contribution

1. 복잡한 기하학적 구조를 5D neural radiance fields로 표현. 이를 위해 기본 MLP 네트워크 사용
2. 고전적인 볼륨 렌더링 기법을 기반으로 미분 가능 렌더링 절차를 제안
3. 각 입력 5D 좌표를 고차원 공간으로 매핑하는 위치 인코딩 방법을 사용

위의 Contribution은 논문의 설명을 다하고 다시 한번 설명하면서 하나하나 의미를 파악해보도록 하겠습니다.

Related Work

Neural 3D shape representations

3D 형상을 신경망을 사용하여 표현하는 방법, 즉 3D 공간의 좌표 (x, y, z)를 입력받아 해당 지점의 특성을 예측하는 신경망을 학습하는 것입니다.

기존의 연구들

Implicit Representation

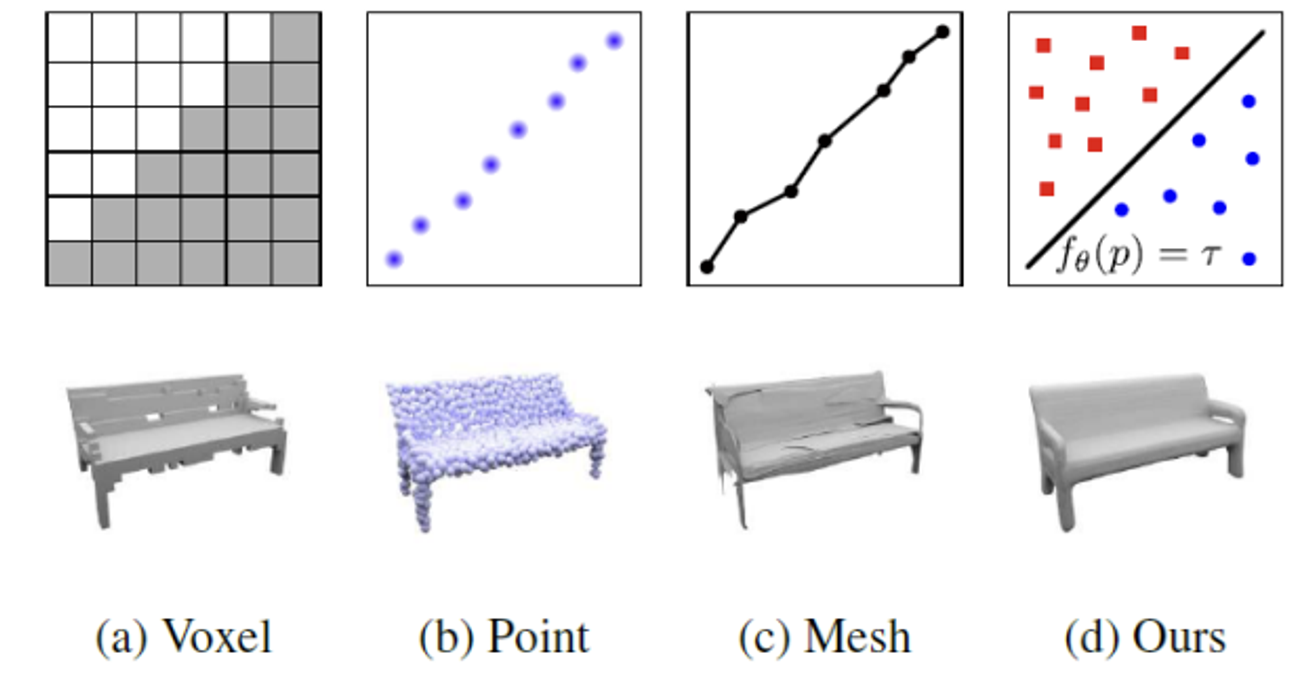
Voxel: 3차원 공간을 grid로 나눴을 때 각각의 공간을 차지하는가 차지하지 않는가(0 or 1)

Point: grid없이 점들의 집합으로 나타내는 것

Mesh: 표면이 어떻게 생겼는가를 표현하는 것

Implicit Representation: 객체의 경계면을 기준으로 값을 a와 b로 나누는 것. 그 기준은 함수를 이용해서 구한다.

실제 3D 기하학 정보(ground truth 3D geometry)에 접근해야한다는 한계가 존재했습니다.

후속 연구로 3D 형상 없이 2D 이미지만으로 신경만 기반 3D 형상을 최적화 할 수 있는 방법이 개발됐습니다. 하지만 여전히 간단한 형상에만 적용되었고, 복잡한 형상을 표현하는 데 한계가 있었습니다.

View synthesis and image-based rendering

Dense Sampling: 다양한 각도에서 매우 많은 수의 이미지를 촬영하는 방법

→ 단순히 interpolation을 이용해서 새로운 시점을 재구성 할 수 있습니다.

Sparse View Sampling: 다양한 각도에서 적은 수의 이미지를 촬영하는 방법

→ Novel View Synthesis(새로운 시점 생성): 적은 수의 이미지로부터 새로운 시점의 이미지를 생성하는 기술

Gradient-based Mesh Optimization는 입력 이미지로부터 mesh를 최적화하는 방법으로 gradient descent를 사용합니다. 하지만 Local Minima or poor conditiong 등 최적화가 어려워지는 한계가 존재했습니다.

Volumetric representations: 3D 공간을 작은 단위(예: voxel)로 나누어 그 단위마다 색상이나 밀도 등의 정보를 저장하는 방식

대규모 데이터셋을 학습해서 volume representation을 예측하는 다양한 연구들이 최근에 등장했습니다.

하지만 고해상도 이미지를 얻기 위해서는 grid를 더 세밀하게 샘플링해야 하고 학습을 더 많이 하는 등 시공간 측면에서 비효율적이었습니다.

NeRF: MLP를 이용해서 고해상도의 이미지와 적은 저장공간을 차지하는 모델을 개발 했다고 논문에서 밝히고 있습니다.

Neural Radiance Field Scene Representation

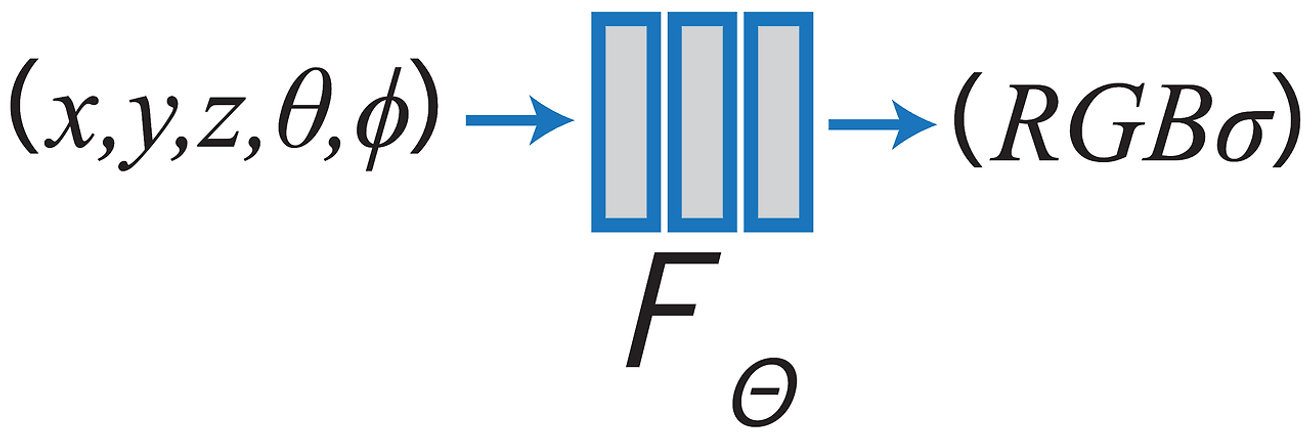
입력값: 5D-vector

3D 위치 정보 $x = (x,y,z)$, 2D 방향 정보 $(θ, φ)$

방향 정보의 부연설명

θ: z축을 기준으로 측정되는 각도로 0~π까지의 각도를 갖는다

• 0: z축의 양의 방향, π: z축의 음의 방향

φ: xy평면에서 측정되는 각도로 0~2π까지의 각도를 갖는다

• 0: x축 양의 방향, π/2: y축 양의 방향, π:x축 음의 방향 ..

출력값: 해당 점의 색깔(c)와 volume density(σ)

색깔 정보 $c=(r,g,b)$

위의 영상을 통해서 간단하게 NeRF의 작동원리를 확인하실 수 있습니다.

입력값과 출력값을 매핑하는 MLP network $F_{\theta}$를 학습시키는 것입니다.

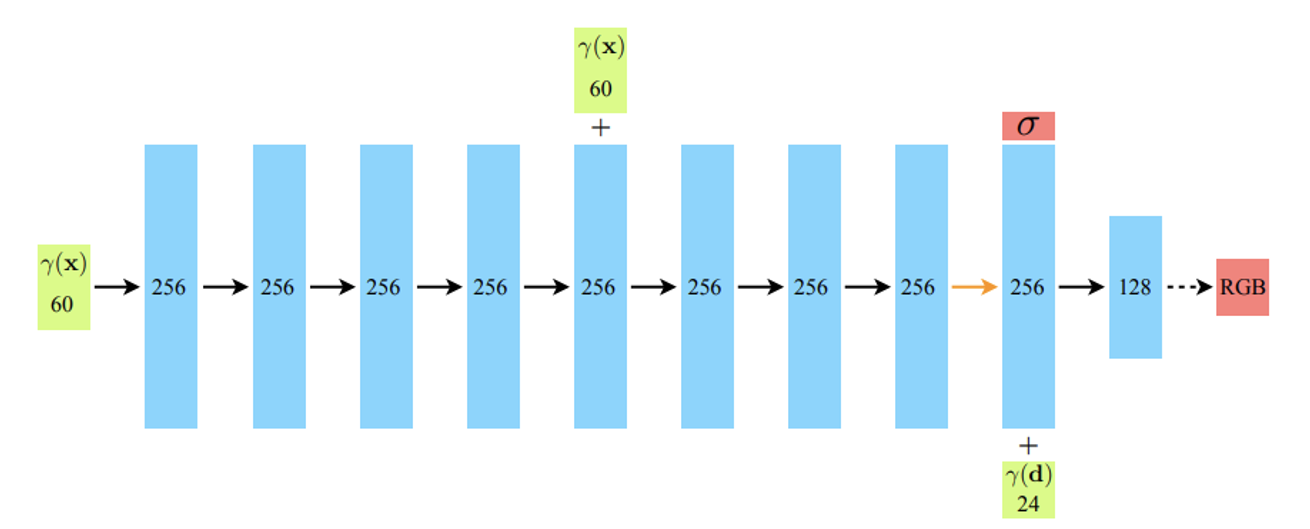
Network의 형태는 단순합니다. 8개의 fully-connected layer를 통해서 density값(빨간색)을 얻고, density값과 direction정보를 합쳐서 최종적으로 색깔(c)를 예측합니다.

예시

입력값: (x,y,z) → (1.0, 2.0, 3.0) / (θ, φ): θ = π/4, φ = π/2

출력값: σ → 0.8 / c(r,g,b) → (0.2, 0.4, 0.6)

Volume Rendering with Radiance Fields

고전적인 Volume Rendering 원리를 사용하여, NeRF는 장면을 통과하는 광선의 색상을 계산합니다.

Volume Density (밀도, σ(x)): 위치 x에서의 밀도 σ(x)는 광선이 해당 위치의 미소한 입자에서 멈출 확률

Camera Ray (카메라 광선, r(t)): 카메라의 원점 o에서 시작하여 방향 d로 진행. $r(t) = o + td$ (t: 광선의 진행 거리)

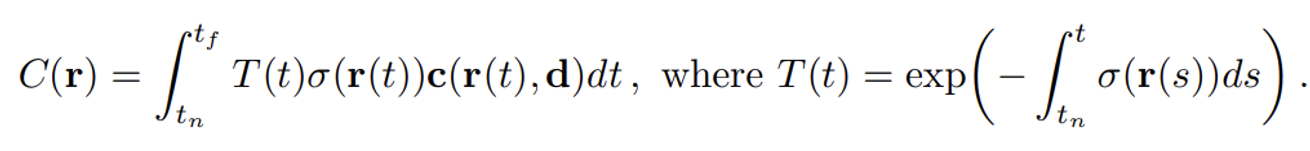
T(t): 광선이 t 지점까지 도달할 확률, 즉 tn에서 t까지의 경로 동안의 정보들을 모두 더해준다.

σ(r(t)): 위치 r(t)에서의 밀도입니다. 이는 해당 지점에서 광선이 멈출 확률
c(r(t),d): 위치 r(t)에서 방향 d로 방출되는 방사성(색상)

∫tntf: 광선의 시작 지점 tn에서 끝 지점 tf까지의 적분

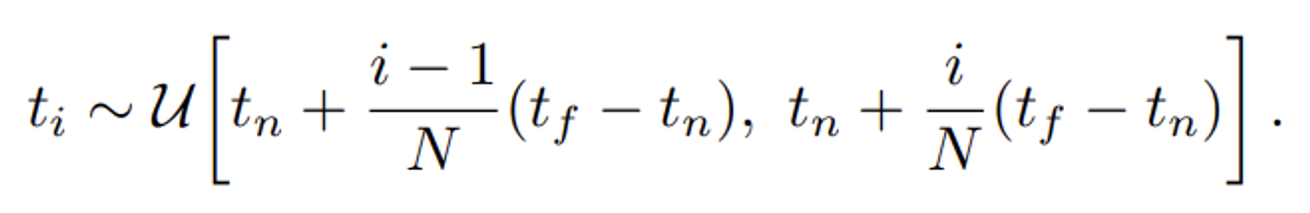
Deterministic Quadrature은 일정한 간격으로 고정된 지점에서 함수를 평가하여 적분을 근사하는 방법입니다. 고정된 지점의 함수 값을 계산하므로, 고해상도를 표현하는데 한계가 있습니다.

startified sampling: 전체 데이터를 여러 하위 그룹(층)으로 나눈 다음, 각 그룹에서 샘플을 무작위로 선택하는 방법

bin: 연속된 데이터를 구간으로 나누는 방법

이에 랜덤 샘플링인 strtified sampling을 사용하여 각 bin 마다 일정 간격으로 샘플링을 하지만, bin 내에서는 랜덤하게 샘플 포인트를 생성

위에서 설명한 것처럼 사실 적분은 모든 데이터들에 대해서 더한 값 즉 연속 적분 방식입니다. 하지만 실제 데이터들의 분포와 계산을 위해서 Discrete Sampling Approach(이산 샘플링 방식)을 실제로는 사용합니다(실제 구현 방식).

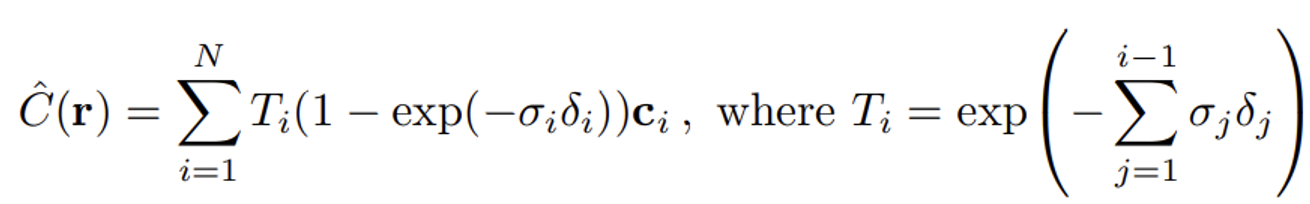
$T_i$: 이 값은 광선이 i번째 샘플 지점까지 도달할 확률

$1−exp(−σ_iδ_i)$: i번째 샘플 지점에서의 alpha 값, 즉 광선이 그 지점에서 멈출 확률

$c_i$: i번째 샘플 지점에서의 색상 값

$σ_i$: i번째 샘플 지점에서의 밀도 값

$δ_i$: 인접한 샘플 지점 간의 거리

Optimizing a Neural Radiance Field

지금까지 설명한 방법으로 새로운 시점에서의 이미지를 생성하는 성능은 좋지 않다고 논문에서 밝혔고, 이에 추가적인 최적화 기법을 사용했다고 설명했습니다.

Positional encoding

딥러닝은 예측할 때 lower frequency에 편향됐습니다. 왜냐하면 lower frequency는 주로 천천히 변하는 큰 패턴인데, 변동이 적어 학습이 더 안정적이기 때문입니다.

고해상도의 이미지를 만들기 위해서는 이러한 한계를 극복해야 합니다. 이에 논문의 저자는 high frequency 정보인 positional encoding 방식을 추가했습니다.

transformer에서도 사용된 방식으로 여기서 positional encoding(r)은 R차원의 정보를 $R^{2L}$의 고차원으로 매핑해줍니다.

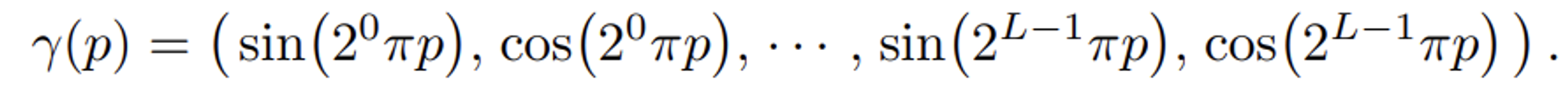
여기서 p는 x또는 d의 각 성분을 나타냅니다. 또한 각 성분은 [-1,1]까지의 값을 갖도록 정규화 되어있습니다.

x에는 L=10(20차원 벡터)으로, d에는 L=4(8차원 벡터)로 실험을 통해서 설정했다고 밝혔습니다.

Hierarchical volume sampling

기존에도 설명했지만, 광선(ray)경로를 따라 일정한 간격으로 샘플을 추출해서 네트워크를 학습하는건 비효율적입니다. 따라서 논문의 저자는 계층적 표현을 통해서 이를 해결했다고 밝혔습니다. 우선 Coare Network를 통해서 대략적인 샘플을 평가하고, Fine Network를 통해서 더 세밀한 샘플링을 수행했습니다.

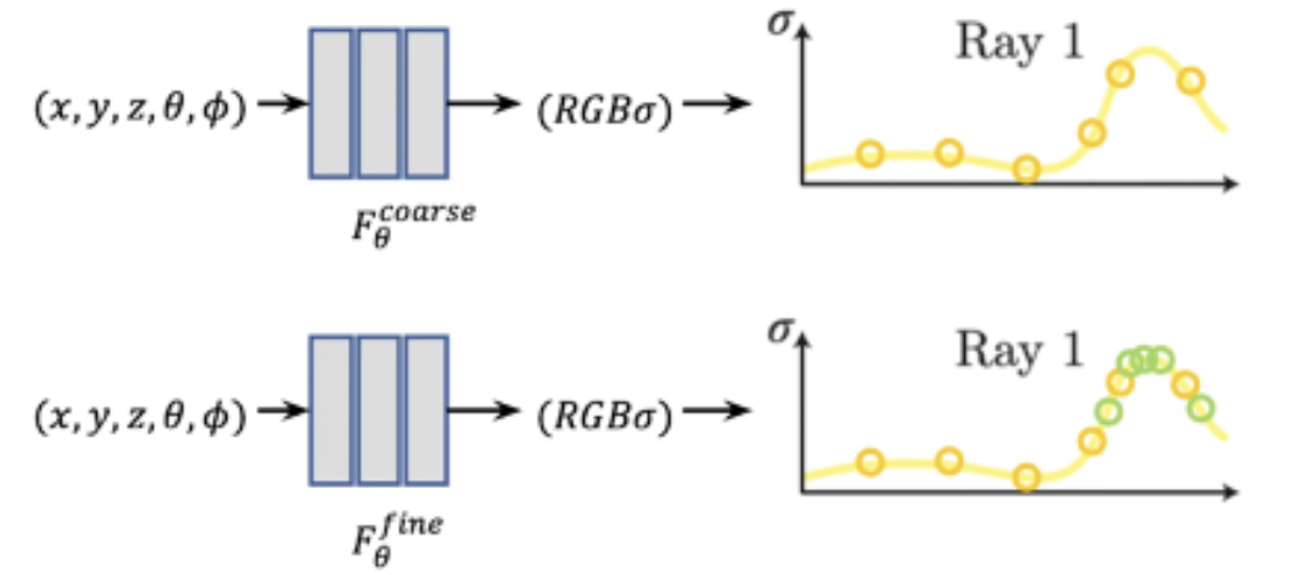
Coarse Network

startified sampling을 통해서 $N_c$개의 위치를 샘플링합니다. 이 샘플들을 바탕으로 가중치 wi(c 계산 방법과 동일)를 계산합니다.

Fine Network

가중치 wi중 높은 부분의 $N_f$개의 새로운 샘플 위치를 선택합니다. 이후 $N_c + N_f$개의 샘플 위치에서 Fine 네트워크를 학습

실험을 통해서 $N_c$는 64개, $N_f$는 128개로 설정했습니다.

Loss Function

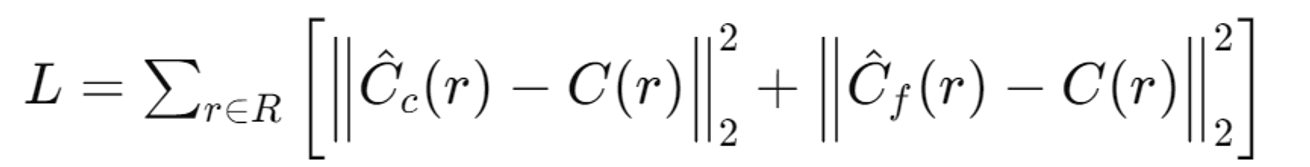
렌더링된 색상과 실제 색상 간의 차이를 최소화.

Coarse와 Fine 네트워크 모두에 대해 손실을 계산합니다.

• R: 각 배치에서 선택된 광선들의 집합
• C(r): 광선 r에 대한 실제 RGB 색상 값
• $\hat{C}_c(r)$: Coarse 네트워크가 예측한 광선 r의 RGB 색상 값
• $\hat{C}_f(r)$: Fine 네트워크가 예측한 광선 r의 RGB 색상 값

Results

Dataset & Comparisons & Discussion 생략

1~4: PE(Positional Encoding), VD(View-dependence), H(hierarchical sampling)의 유무에 따른 성능비교

VD부가 설명

View-Dependence (시점 의존성): 물체의 외관이 보는 시점에 따라 달라지는 현상을 의미

시점 의존성이 있는 경우

• 특정 위치에서 빛이 다양한 방향으로 방출되는 모습을 모델링할 수 있습니다. 예를 들어, 유리 표면이 빛을 반사하는 경우, 보는 각도에 따라 다르게 보이는 특성을 반영할 수 있습니다.

시점 의존성이 없는 경우

• 모든 방향에서 동일한 색상을 출력하게 되어, 물체의 반사나 굴절 같은 특성을 표현하지 못합니다. 이는 모델이 현실적인 이미지를 생성하는 데 한계를 가집니다.

5~6: 이미지의 개수에 따른 성능 비교

7~8: PE의 L의 수에 따른 성능 비교

정리

Contribution

1. 복잡한 기하학적 구조를 5D neural radiance fields로 표현. 이를 위해 기본 MLP 네트워크 사용
2. 고전적인 볼륨 렌더링 기법을 기반으로 미분 가능 렌더링 절차를 제안
3. 각 입력 5D 좌표를 고차원 공간으로 매핑하는 위치 인코딩 방법을 사용

이제 다시 한번 Contribution을 보겠습니다.

1. 5D vector(위치 + 방향)에 대해서 간단한 MLP 구조를 사용해서 Color + depth 정보를 파악하는 모델
2. 미분 가능하게 설정하여 학습이 가능
3. positional embeding 값을 추가해서 고차원 공간으로 매핑

지금까지 내용을 잘 이해하셨다면 충분히 Contribution의 내용들을 이해할 수 있을겁니다.

한계

하지만 NeRF모델의 한계는 존재했습니다.

가장 큰 문제는 시간입니다. 다른 시점에서 본 이미지를 생성하기 위해서는 5시간의 학습시간이 걸리는 점이 가장 큰 한계입니다.

또한 시계탑 모형처럼 4면이 동일한 경우 정면을 잘 찾지 못한다거나, 같은 물체더라도 시간이나, 날씨의 영향에 따른 환경 변화의 영향도 많이 받습니다.

개인적인 의문

MLP의 단점은 아마 누구나 알거 같습니다. 바로 지역적인 정보를 활용하지 못한다는 점입니다. 현재는 MLP를 사용하기때문에 이러한 단점들을 극복하는 논문이 나왔는지 추후에 찾아보고 업로드 하도록 하겠습니다.