Generative Modeling by Estimating Gradients of the Data Distribution[2] 논문 리뷰

이한결·2024년 12월 23일

논문 저자 Yang Song님 논문 리뷰 정리 글: https://velog.io/@guts4/Generative-Modeling-by-Estimating-Gradients-of-the-Data-Distribution1-Yang-Song-Blog-%EB%A6%AC%EB%B7%B0

위의 블로그에 포스팅된 글이 조금더 간단한 내용에 대해서 정리를 해뒀고, 아래의 글은 논문의 흐름에 따라 정리한 글입니다. 개인적으로 위의 글을 읽고 아래 내용을 읽으면 더 많은 도움을 받을 것 같습니다.

Likelihood-based methods vs Adversarial networks

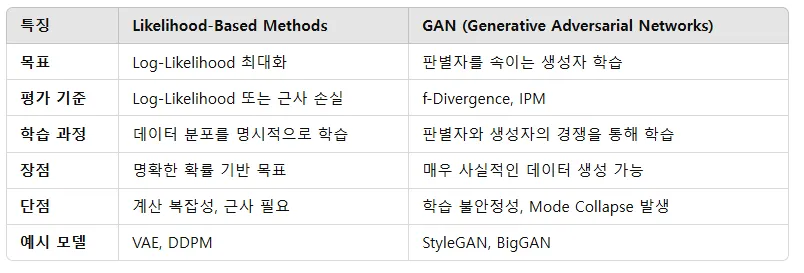
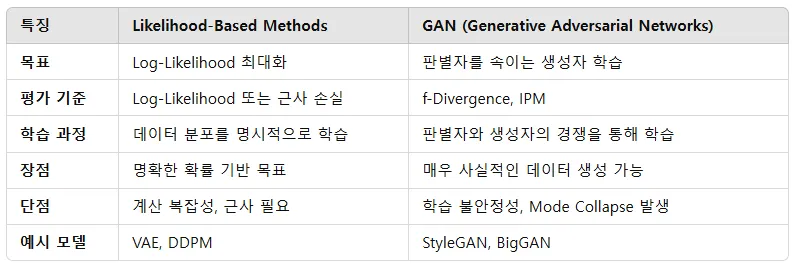
시작은 블로그의 내용처럼 2가지 최근 모델의 큰 흐름에 대해서 설명했습니다. Likelihood-based model들은 likelihood를 최대화하면서 학습이 진행되고, adversarial에서는 f-divergence와 IPM(Integral Probability Metrics)를 최소화하면서 학습이 진행됩니다.

Likelihood-based model은 specialized architecture를 사용해서 계산 비용이 높고(Autoregressive model은 데이터를 순차적으로 처리해야 하므로), 유연성이 부족(Normalizing flow에서는 invertible한 아키텍처를 필요로 함) 합니다. 또한 likelihood를 직접 구하기 못해서 surrogate loss(근사 loss)를 사용함으로써 오차가 발생할 수 있습니다.

GAN에서는 잘 아시다시피 discriminator를 속이기만 하면되기 때문에, 다양성이 떨어지고 현실적인 하나의 이미지만 생성하는 mode collapse 문제가 발생합니다.

이에 새로운 score based model을 제안했습니다. Vector field라는 log data density가 가장 많이 증가하는 방향을 가리키는 벡터 필드를 학습하는 것입니다. 이를 학습하기 위해서 score matching과 함께 neural network을 학습 시키고, Langevin dynamics를 이용해서 샘플링을 진행했습니다.

하지만 위의 방식으로 진행할 경우 2가지 문제점이 생겼습니다. 첫번째로 저차원의 데이터로 인해서 Score Matching의 학습이 일관되지 않을 수 있고, 두번째로 데이터가 부족한 영역에서 Score function이 부정확해져서 Langevin Dynamics 샘플링이 부정확해집니다.

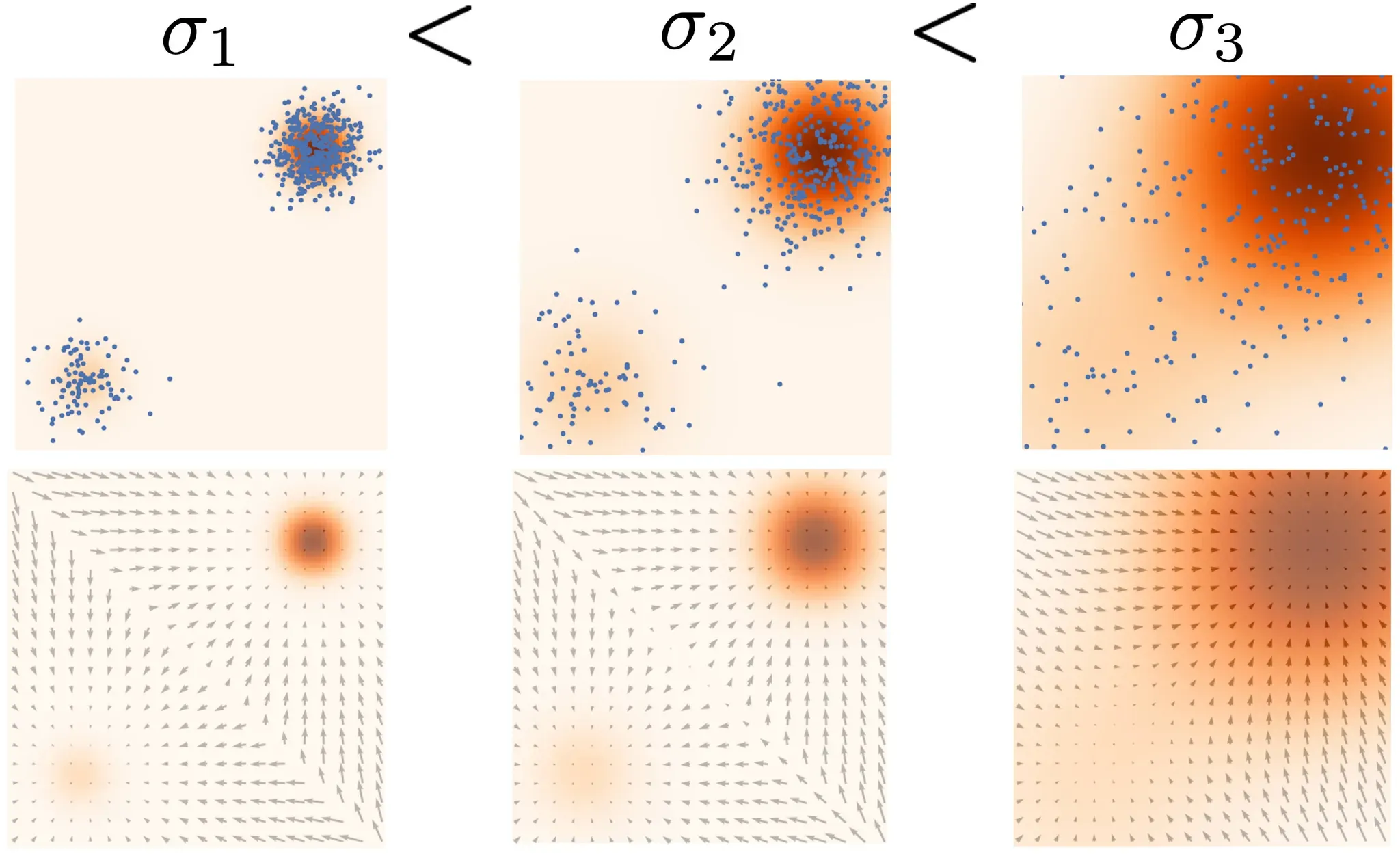
2가지 문제를 해결하기 위해서 다양한 크기의 random Gaussian을 데이터에 추가하는 방식을 제안했습니다. 큰 노이즈에서부터 점차 노이즈를 줄이는 annealed version of Langevin dynamics 적용시킴으로서 dimension과 density 부분에서 모두 적은 부분을 채워줄 수 있는 역할을 합니다. 사진에서 오른쪽에서 왼쪽으로 진행되는데, 노이즈의 크기가 컸을 때 데이터의 분포가 퍼져있고, 점점 줄일수록 한 곳으로 모이는 것을 알 수 있습니다.

논문이 기여한바는 다음과 같습니다

특별한 제한이나 아키텍처 구조 또는 approximation 없이 쉽게 학습할 수 있다.
다른 모델들과 벤치마크 비교 결과 비슷하거나 더 높은 결과를 나타냈다.

이중에서 아마 1번이 가장 큰 기여점인거 같습니다. 위에서도 말했지만 liklihood-based model들은 제약조건(VAE-ELBO)이나 제한된 아키텍처들이 한계점이었고, GAN 같은 경우도 mode collapse 문제가 한계점이었는데 두가지 한계를 모두 극복했기 때문입니다.

Score-based generative modeling

모든 데이터들은 독립적이고 동일하게 분포된(i.i.d) 상태라고 보고, 확률 밀도의 score를 $\nabla_x \log p(\mathbf{x})$ 로 정의하겠습니다. Score network( $s_{\theta}$ )는 데이터의 score를 학습하게 됩니다.

Score matching for score estimation

“Estimation of non-normalized statistical models by score matching”의 논문에서 발표한 score matching을 사용하면 데이터 분포를 직접 모델링 하는 대신 score network( $s_{\theta}$ )를 이용해서 $\nabla_x \log p(\mathbf{x})$ 를 학습할 수 있습니다.

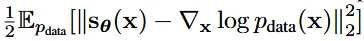
위의 수식을 통해서 score network는 데이터 분포에 log를 취한 gradient를 기반으로 최적화되게 됩니다. 하지만 우리는 데이터 분포를 정확히 알지 못하기 때문에 전개와 적분을 이용해서 아래의 수식을 얻게 됩니다.

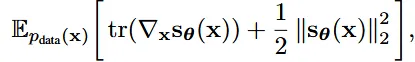
결론적으로 데이터의 분포를 알지 못해도 score network를 통해서 데이터의 분포를 근사화해서 얻을 수 있게됩니다. 하지만 위의 수식은 계산량이 너무 많아서 딥러닝에 쉽게 적용할 수 없습니다.

Denoising score matching

Denoising score matching은 score matching을 변형한 형태로서 복잡한 계산인 tr( $\nabla_xs_{\theta}(x)$ )를 피한 형태입니다. 핵심 아이디어는 우리가 알지 못해서 전개와 적분을 이용해서 얻은 Trace식을 피하는 것입니다. 피하기 위해서는 첫번째 수식에서 두번째 수식으로 넘어가지 않으면 되는데, 넘어가지 않으려면 우리가 데이터의 분포를 알고 있어야합니다.

그러면 데이터의 분포를 어떻게 알 수 있을까요? 여기서 핵심적인 개념이 우리가 알고있는 분포로 바꾸는 아이디어 입니다. 우리는 정규분포를 너무나 잘 알고 있고, 데이터의 분포를 정규분포로 바꾼다면 수식의 변환이 없어지고 그러면 계산이 쉬워질 것입ㄴ다.

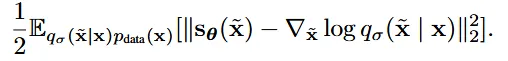
위의 수식이 핵심아이디어를 적용한 결과입니다. $\mathbf{\tilde{x}}$ 가 노이즈가 추가된 x데이터이고, $(\mathbf{\tilde{x}}|x)$ 는 데이터 x에 추가된 노이즈입니다. 위의 수식을 자세히 보면 노이즈가 추가된 데이터를 기반으로 학습하는 것이 아닌 추가한 노이즈를 기반으로 학습하는 것을 알 수 있습니다.

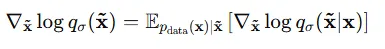
왜냐하면 전체 노이즈가 추가된 분포( $\mathbf{\tilde{x}}$ )는 추가된 노이즈의 기댓값과 동일하기 때문에 2가지가 같은 방향으로 학습되는 것입니다. 결론적으로 우리는 우리가 아는 분포를 이용해서 계산 비용을 줄이면서 score matching을 계산할 수 있게 됐습니다.

Sliced score matching

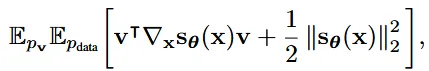
Denoising socre matching(DSM)에 이어서 계산 비용을 낮추기 위한 2번째 방법인 Sliced score matching 방법입니다. Trace항을 모든 차원에서 계산하는 대신 무작위 방향으로 projection된 gradient를 사용해 trace를 근사시키는 방법입니다. DSM 방법에 비해 계산 비용이 4배 높다는 단점이 존재하지만 노이즈를 추가하지 않는다는 장점도 존재합니다.

Sampling with Langevin dynamics

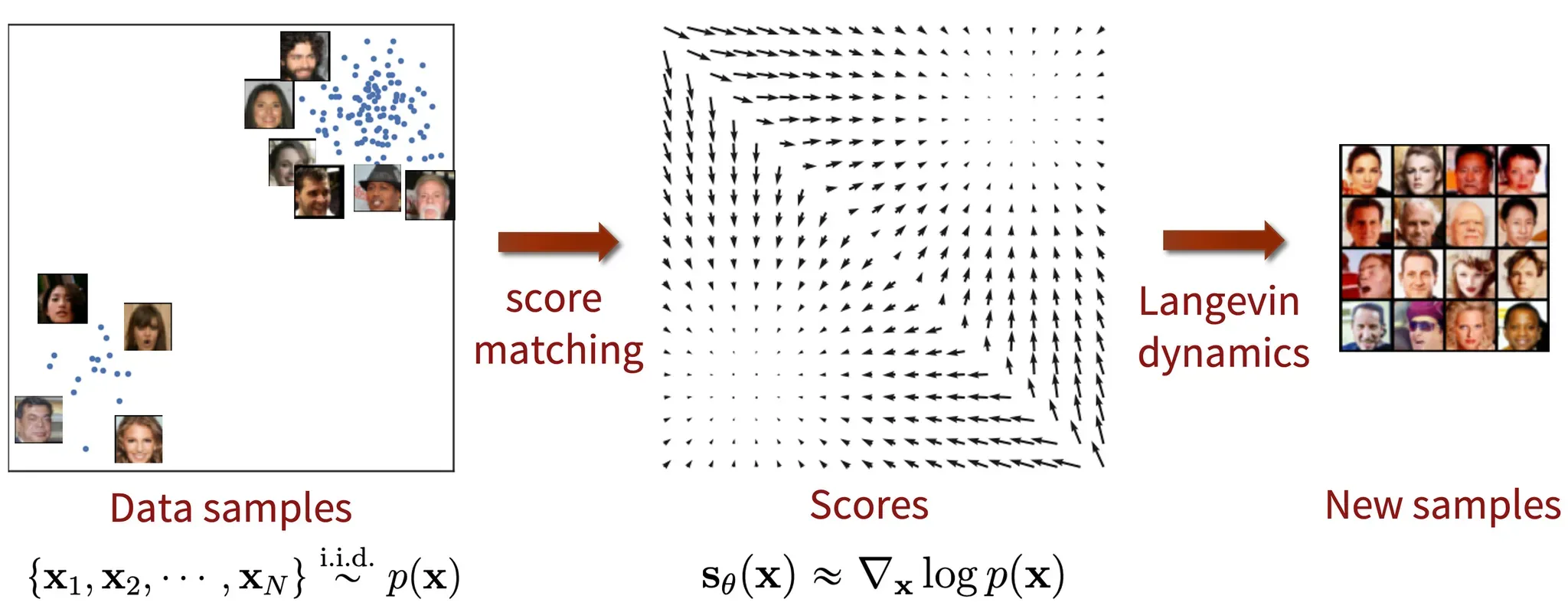
Langevin dymamics는 score function만을 이용해서 샘플링이 가능한 방법입니다.

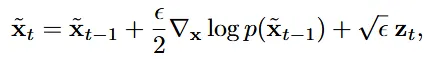
위의 수식은 직관적으로 이해하실 수 있을 겁니다. 어떤 데이터 점에서 이전 단계의 score function(화살표)를 따라서 다음 단계로 이동하는 것입니다. 이때 $z_t$ 는 정규분포를 나타내고, $\epsilon → 0$ 와 $T→\infty$ 라는 가정하에 완벽한 샘플을 만들 수 있습니다.

핵심 아이디어는 Langevin dynamics는 score function만을 이용해서 샘플링이 가능하기 때문에, 모델을 학습시킬 때 score function만 학습해도 된다는 점입니다.

Challenges of score-based generative modeling

The manifold hypothesis

실제 세계의 데이터들이 고차원에 존재하지만, 실제로 데이터들을 결정 짓는 요소들(사람의 경우 얼굴의 생김새 등)은 일부 이므로 이러한 요소들은 저차원에 존재합니다. 따라서 Ambient space(전체 공간)을 기준으로 데이터들은 특정 공간에만 분포하게되는 Manifold 현상이 발생합니다.

이렇게 될경우 첫번째로 Manifold 구간에서만 score가 정의되고, 나머지 부분에서는 score가 정의되지 않는 문제가 발생합니다. 두번째로 데이터의 분포가 일관되지 않기 때문에 score matching의 결과도 일관되지 않은 결과를 제공할 수 있습니다.

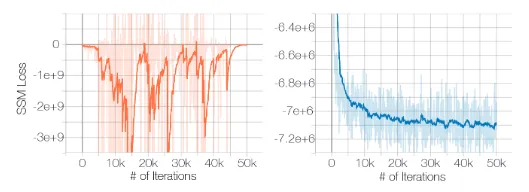
위의 사진은 왼쪽이 Sliced score matching(SSM), 오른쪽이 Denoising score matching(DSM)의 CIFAR-10을 이용한 실험 결과입니다. 왼쪽은 노이즈를 추가하지 않았기 때문에 loss가 들쑥날쑥 하는 것을 알 수 있고(ManiFold일 때는 결과가 좋고), 오른쪽의 loss는 학습할수록 수렴하는 것을 알 수 있습니다.

Low data density regions

Inaccurate score estimation with score matching

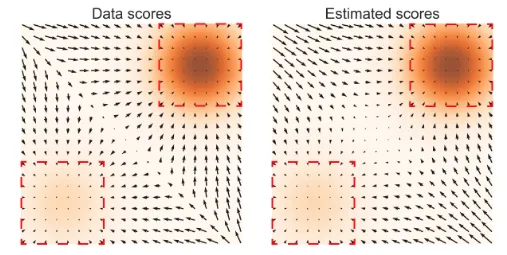
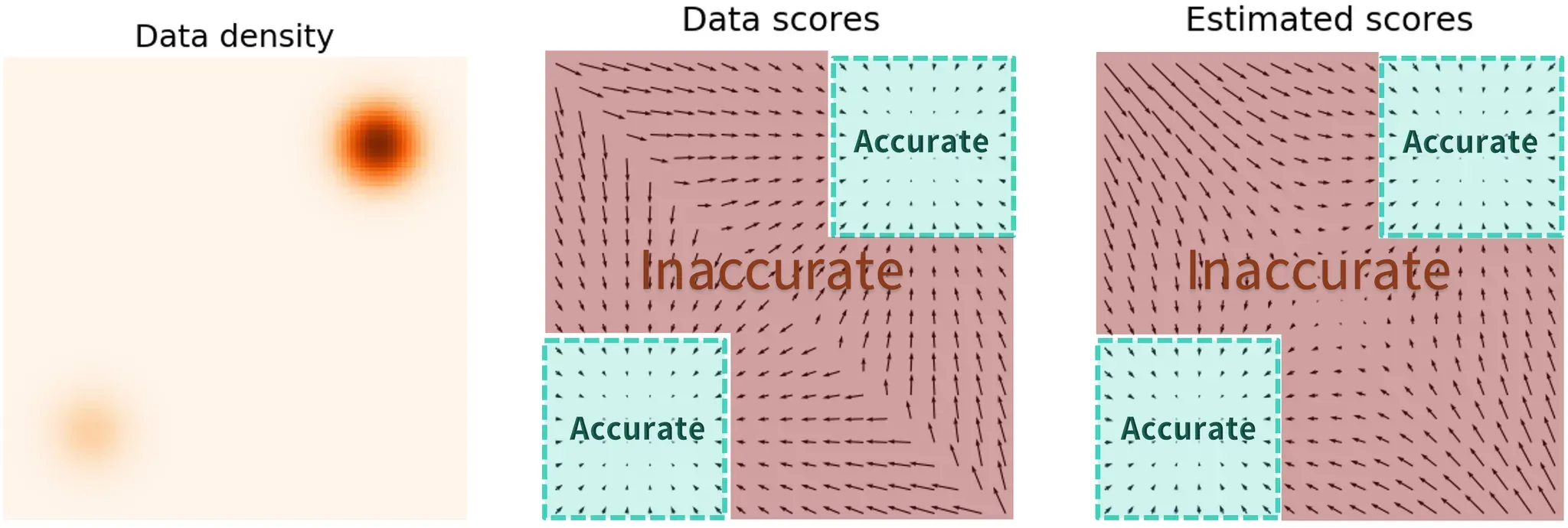
이전에는 데이터의 차원을 결정하는 요소가 적기때문에 학습이 잘안되는 내용을 설명했습니다. 차원과 비슷하지만 조금 다른 개념인 density(밀도)에 대해서 설명해 보겠습니다. 사진처럼 density에서도 데이터들은 특정 영역에만 몰려서 존재합니다. 따라서 이 역시 score matching이 잘 학습되지 않는 요소 중 하나입니다.

사진에서 색깔이 진할수록 데이터가 많이 몰려있다고 보시면됩니다. 오른쪽 위는 데이터가 많이 있어서 Data score와 Estimated score를 비교해도 화살표가 비슷하게 나타나 있습니다. 하지만 왼쪽 아래의 경우 데이터가 별로 없어 화살표의 크기와 방향이 Data score와 Estimated score에서 차이가 나타나는 것을 확인할 수 있습니다.

Slow mixing of Langevin dynamics

Low density regions(가운데)에서 Langevin dynamics를 실행시킬 경우 score(화살표)가 명확하지 않아서 relative weight를 찾기 힘들 것입니다. relative weight는 원래 남자와 여자의 비율이 5:5일 경우 비 비율을 찾기가 어렵다는 뜻입니다.

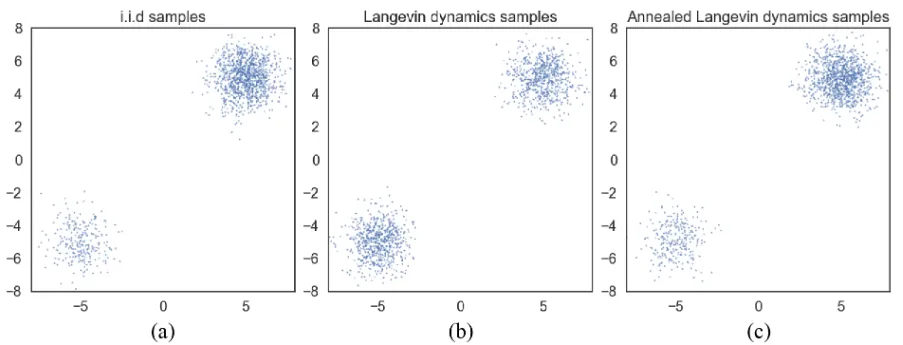
위의 그림에서 (a)는 Ground truth (b)는 Gaussian을 더해서 exact(정답) score를 기반으로 Langevin dynamcis sampling(쉽게 말하면 이전”The manifold hypothesis”에서 설명한 노이즈를 추가하는 방식 적용) (c)는 exact score를 기반으로 Annealed Langevin dynamcis 적용.

그림을 설명하면 (b)는 데이터의 분포가 원본과 다른데, Annealed Langevin dynamics를 사용한 (c)는 데이터의 분포과 원본과 같은 것을 확인할 수 있습니다.

Noise Conditional Score Networks: learning and inference

위의 문제들을 보면서 대강 이들을 어떻게 극복할지 알 수 있었습니다. low dimension 문제(데이터를 결정 짓는 요소들이 적은 문제)는 gaussian noise를 추가함으로서, low density region 문제(데이터가 가운데서 시작해서 못 빠져나가는 현상) 역시 gaussian noise를 추가함으로서 다른 구역으로 넘어가고 마지막으로 데이터의 relative weight를 맞추기 위해서 annealed langevin dynamics sampling을 적용하는 방법 이렇게 크게 3가지 일 것입니다.

Noise Conditional Score Networks

${{σ_i}}$ 는 i가 커질수록 노이즈가 작아지도록 설계 되어 있습니다. $q_σ(x)$ 가 노이즈가 추가된 분포입니다. 초기의 큰 노이즈들은 low density region에서 탈출 시키는 역할을 해주고, 작은 노이즈들은 데이터 분포를 더 세밀화하게 해줍니다. 입력값으로 x와 σ를 받는 Noise conditional score network(NCSN)은 다양한 노이즈를 통해서 이전 데이터 분포의 한계들을 극복할 수 있게해준 모델입니다.

NCSN은 U-Net 모델을 기반으로 설계 되었고, 이전 image generation task에서 사용했던 conditional instance normalization[Appendix A 참조]을 적용했습니다.

Learning NCSNs via score matching

이전에 설명한 sliced와 denoising score matching 방법을 이용해서 NCSN을 학습 시킬 수 있습니다. 그중에서 denoising 방식을 선택해서 더 빠르고 noise-perturbed data distributions에 알맞게 학습할 수 있도록 했습니다.

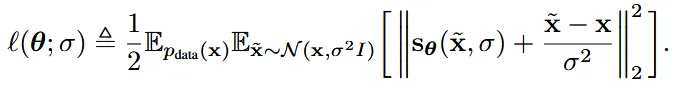
이전에 설명했던 부분에서는 노이즈를 condition으로 받지 않았고, 해당 수식에서는 노이즈를 condition으로 받은 점이 차이점입니다. 결론적으로 score matching을 이용해서 노이즈의 gradient를 예측한다! 라고 쉽게 생각하시면됩니다.

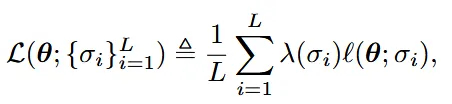
이전에 설명했던 것처럼 노이즈를 더한 분포는 더한 노이즈의 기댓값을 이용해서 구할 수 있습니다. 그 과정이 위의 식을 통해서 나타나져 있습니다. 이때 가중치 함수λ( $σ$ )는 $σ^2$ 으로 나타낼 수 있습니다. 노이즈에 다라서 Loss항의 기여도가 동일하게 나타나도록 합니다. 직관적으로 노이즈가 클 경우 high density region에서 멀어져서 화살표가 커지고, 노이즈가 작을 경우 high density region에 가까워져서 화살표가 작아지는 현상을 막는 것입니다.

NCSN inference via annealed Langevin dynamics

NCSN 학습 이후 annealed Langevin dynamics를 진행합니다.

알고리즘은 간단합니다. 시작은 고정된 prior distribution( $\tilde{x}_0$ )에서 시작해서 i가 1~L까지 노이즈를 점점 작아지게 하면서 Langevin dynamics를 진행하는 것입니다.

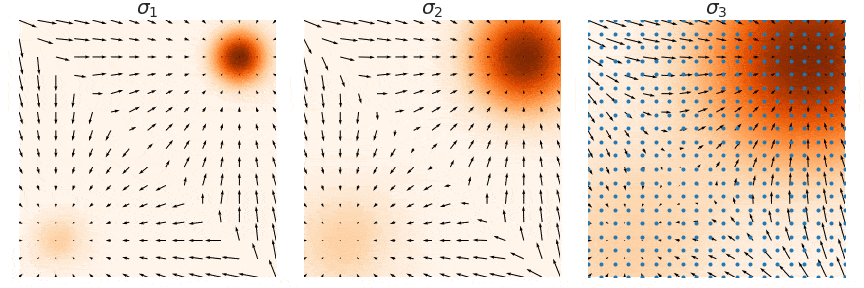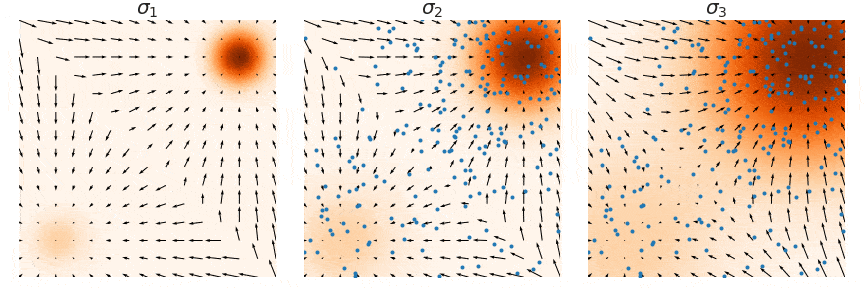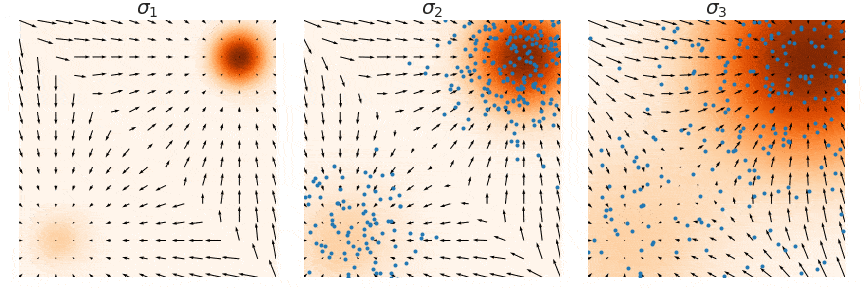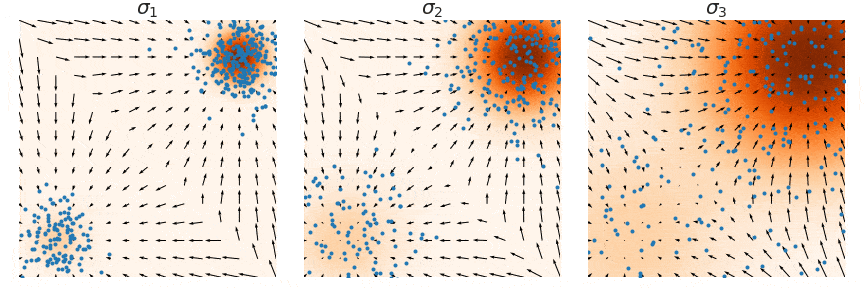
시각적으로 위와 같은 형태로 샘플링이 진행될 것 입니다. 초기의 큰 노이즈로 인해서 데이터들이 whole space에 골고루 퍼지게 되고, 노이즈가 작아질수록 gradient를 기반으로 더 세밀한 부분으로 이동하게 됩니다.

Experiments

annealed Langevin dynamics에서 사용한 L 값은 10으로 사용했습니다. 이후 데이터를 crop하고 resize하는 등의 setup을 진행했으며 자세한 사항은 논문 Appendix A,B를 참고하시면 됩니다.

위의 사진은 다양한 데이터셋에서 이미지 생성 결과입니다.

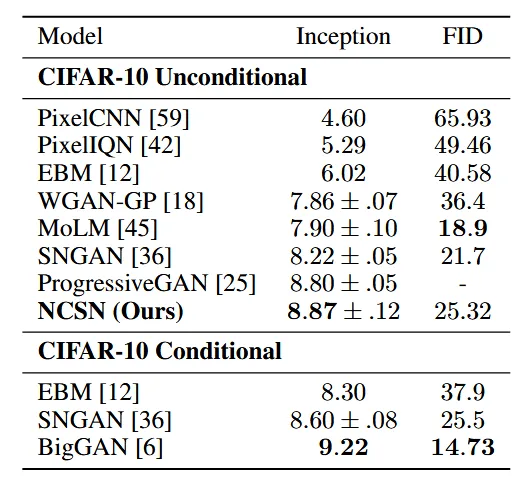
위의 Table은 inception과 FID score를 CIFAR-10에 대해서 비교한 결과입니다. Unconditional model의 경우 NCSN이 SoTA를 달성했습니다. 심지어 conditional model인 EBM보다 성능이 더 좋은 것을 확인할 수 있습니다.