3D Mesh를 text prompt에 맞게 변형하되 원래 3D 객체의 정체성을 유지하면서 원하는 스타일로 형태를 바꾸는 방법을 제시했습니다. 기존 모델들은 너무 보수적이거나 과한 접근을 했지만 Geometry in style은 normal vector를 기반으로 변형을 해서 섬세하면서도 안정적인 변형이 가능했습니다.

Related Work

Classical Deformation Representations

대표적인 Mesh를 변형하는 방법으로는 Laplacian surface editing, Gradient field mesh editing, Skinning, ARAP(As-Rigid-As-Possible) 방식이 존재합니다. 이중에서 논문은 ARAP 방식을 사용했습니다. ARAP는 가능한 한 원래 형태를 유지하면서 변형 시키는 방식입니다. Mesh를 rigid body처럼 다루기 때문에 형태는 잘 유지되면서도 자연스러운 변형이 가능합니다.

논문에서 제시한 ARAP를 deep learning에 적용한 dARAP는 기존의 여러 번 반복해서 결과는 얻는 방식과 다르게 한번의 local step + global step으로도 충분히 좋은 결과를 낼 수 있습니다.

Normal-Driven Shape stylization

기존의 법선 기반 스타일 변형은 고정된 법선 템플릿에 의존했지만, Geometry in Style은 텍스트 프롬프트를 통해 더 유연하고 의미 중심의 스타일링이 가능합니다. 또한 part-aware로 다르게 변형할 수 있어서, 더 정교하고 사용자 의도에 맞는 변형이 가능하다는 점이 핵심 차별점입니다.

Neural Shape Manipulation

2D diffusion 모델의 발전으로 3D generation도 2D diffusion prior를 distillation 방식을 이용해서 같이 발전을 했습니다. 대부분 implicit shape representation(SDF, NeRF, Gaussian Splatting) 방식을 사용해서 모델을 계발했습니다.

최근에는 생성뿐만 아니라 Text를 기반으로 3D를 수정하는 방법들도 제시 되고 있습니다. 해당 논문도 Text를 기반으로 3D를 수정하지만 기존 논문들은 단순히 mesh의 vertex 위치를 직접 옮기는(displacement) 방식이지만 해당 논문은 표면의 법선을 회전시키는 간접적인 방식으로 mesh를 변형하고, 결과는 dARAP solver로 계산합니다.

Neural Jacobian Fields

Neural Jacobian Fields(NJF)는 고전적인 미분 기반 mesh 변형 방법을 딥러닝에서 직접 다룰 수 있도록 미분 가능하게 구성했습니다. 해당 논문에서는 mesh의 각 face에 대해 국소적인 변형을 기술하기 위해 Jacobian matrix를 사용합니다(TextDeformer, MeshUp도 이 방식을 사용).

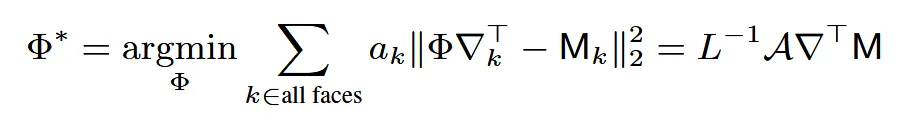
각 face마다 변형 행렬 $M_k$를 정의하고, 전체 메시 정점을 최적으로 변형시키는 $\Phi^*$를 구해야 하는데 이는 위의 수식처럼 포아송 방정식으로 풀 수 있습니다. $a_k$는 면의 면적, $∇_k$는 gradient을 나타냅니다. 위의 수식은 미분 가능하므로 backpropagation에서도 문제 없이 활용할 수 있습니다.dARAP도 포아송 방정식으로 표현할 수 있기 때문에 NJF처럼 미분 가능한 solver를 활용할 수 있습니다.

Mesh Up과 TextDeformer가 NJF 방식을 활용했지만 이들은 Jacobian을 최적화하도록 설계 됬기 때문에 변형 자유도가 너무 높아 원래 형태가 쉽게 망가질 수 있습니다. 이에 반해 dARAP 구조를 활용한 해당 논문은 더 보수적이고 정체성 보존에 유리하게 설계되어 있습니다.

Method

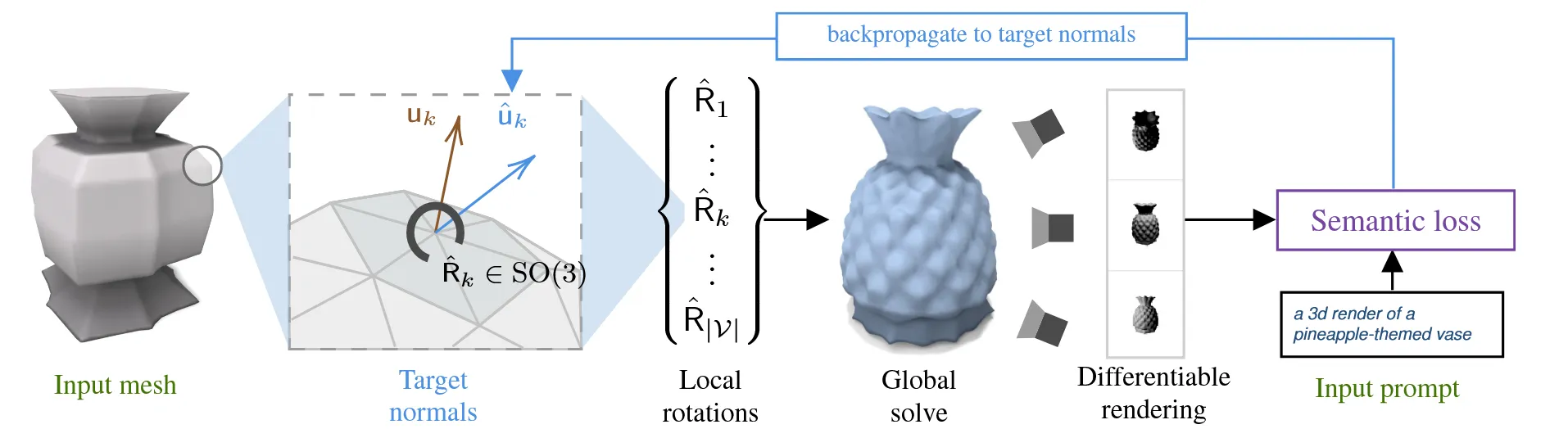
해당 모델의 입력은 Mesh(V,F)와 text prompt이고 출력은 스타일이 반영된 변형 메시 $M^*$입니다.

핵심 아이디어는 vertex들의 normal vector를 먼저 최적화 하는 것입니다. Mesh에 $|V|$개의 vertices가 있다고 할 때 gradient descent는 $|V| X 3$을 직접 optimize해서 target normal vector $\hat{u}$를 얻습니다. 이후 각 정점의 rotation $\hat{R}$을 얻기 위해 $\hat{u}$가 사용됩니다. 마지막으로 rotation matrix를 vertex position에 반영하는 과정을 진행합니다.

정리하면

1. Gradient descent로 target normal vectors($\hat{u}$) 구하기
2. Local Step: Target normal로부터 각 정점의 rotation matrix($\hat{R}$) 구하기
3. Global Step: Rotation matrix로부터 최종 vertex position 계산

여기서 2,3번을 dARAP라고 부릅니다. 기존 ARAP 방식과 다르게 vertex가 아닌 normal vector를 직접 예측하고, 딥러닝을 사용하기 때문에 한번만에 정확한 deformation 결과를 얻을 수 있습니다.

Local Rotations from Normals

우선 target normal vector를 만드는 방법은 해당 논문에서 자세히 설명하지 않았지만, 3D Paintbrush에서 사용한 CSD(Cascaded Score Distillation) loss를 이용해서 text prompt를 잘 반영하는 방법으로 normal들을 gradient descent로 조금씩 조정합니다.

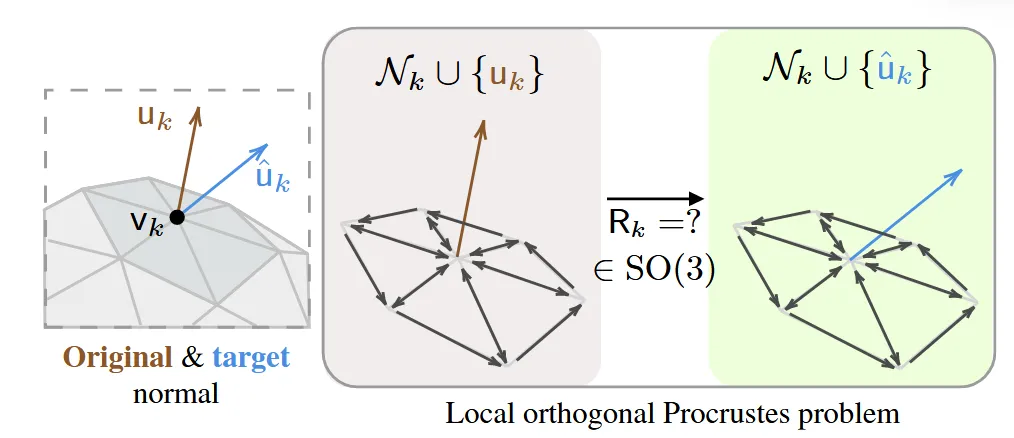
이렇게 target normal vector를 구해도 정점의 위치를 바꿀 수 없습니다. 왜냐하면 법선은 방향 벡터이기 때문에 어떻게 회전해야 될지에 대한 정보가 필요합니다. 이를 구하는 과정이 local step입니다. 위의 그림에서 파란색 화살표를 구했는데 어떻게 갈색 화살표가 회전해야 파란색 화살표 방향으로 바뀌는지를 구하는 과정입니다.

Local step에 대해서 설명하자면 정점 k 주변에는 여러 이웃 정점($v_j, v_i$)이 존재하고, 이들 사이에는 edge vector($e_{ij} = v_i - v_j$)가 있습니다. 원래 mesh의 정점 k의 normal을 $u_k$, target normal은 $\hat{u}_k$일 때 우리는 $\{e_{ij},u_k\}$를 회전시켜서 $\{e_{ij},\hat{u}_k\}$쪽으로 최대한 잘 맞추는 회전 행렬을 찾는 것입니다.

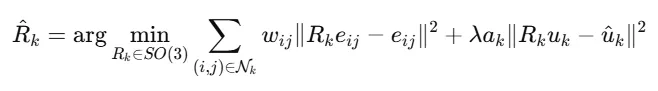
회전 행렬을 찾기 위한 ARAP 에너지 식은 위와 같습니다.

• $w_{ij}$: contangent weight
• $a_k$: 정점 k의 영역 면적(Voronoi mass of vertex k)
• λ: target noraml과 얼마나 일치할지를 결정하는 하이퍼파라미터

위의 수식은 Orthogonal Procrustes 문제, 즉 여러 벡터 쌍이 주어졌을 때 가장 잘 맞게 회전시킬 수 있는 행렬을 찾는 문제입니다. 해당 문제는 SVD로 매우 효율적으로 풀 수 있습니다.

Global Solve from Local Rotations

Rotation matrix를 구했으니 이제 해야 하는 일은 이 회전이 실제로 적용된 것처럼 보이게 vertex position들을 다시 계산하는 것입니다.

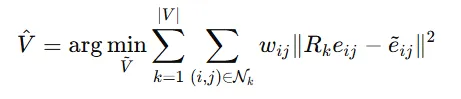
• $R_k$: vertex k의 rotation matrix
• $e_{ij}$: 원래 mesh의 edge 벡터
• $\tilde{e}_{ij}$: 변형 mesh의 edge 벡터
• $w_{ij}$: contangent weight

위의 식은 모든 정점 위치들에 대해 2차식 형태이므로 Linear Least Squares 문제입니다.

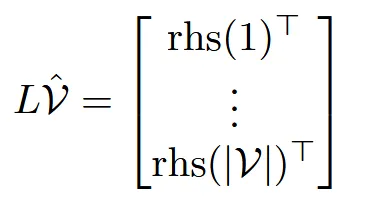
Linear Least Squares를 풀기 위해서 위의 Poisson equation을 사용합니다.

• L: cotangent Laplacian
• $\hat{V}$: 우리가 구하고 싶은 정점 위치 벡터들
• $rhs(k)$: 각 정점에 대응되는 우변 벡터

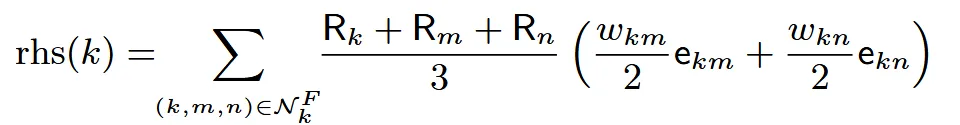
• $N_k^F$: 정점 k에 연결된 삼각형 면들(각 면은 정점 3개: k,m,n)
• $R_k, R_m, R_n$: 해당 면의 세 꼭짓점에 대한 회전 행렬들
• $e_{km}, e_{kn}$: 원래 mesh의 edge 벡터
• $w_{km}, w_{kn}$: cotangent weight

위의 수식은 각 face에서 vertex k 주변 edge들이 해당 회전들에 얼마나 영향을 받는지를 평균적으로 고려하여 vertex k가 움직여야 할 방향을 계산합니다.

Experiments

Properties of Geometry in Style

Generality and expressivity

즉 해당 논문에서는 다양한 형태의 Mesh를 text prompt를 기반으로 다양한 스타일링할 수 있으며, 원하는 부위만을 변형할 수 있습니다.

Identity preservation

원래 Mesh의 고유한 형태, 포즈, 구조를 훼손하지 않고 유지할 수 있습니다. 이는 normal 기반 rotation matrix를 사용했기 때문에 정체성을 유지하면서 부분적인 변형이 가능한 것입니다.

Specificity

Text에서 지시한 세부 스타일을 실제 mesh 구조에 아주 구체적으로 반영할 수 있습니다. 예를들어서 왼쪽 위의 결과에서 종이 접기 스타일의 text를 반영하기 위해서 접힌 자국처럼 보이는 주름이 표현된 것을 확인할 수 있습니다.

Robustness

입력 mesh가 달라도 지정한 스타일을 일관되게 잘 반영할 수 있습니다.

Tunable stylization strength

λ값의 변경을 통해서 스타일을 얼마나 강하게 적용할지를 제어할 수 있습니다.

Limitation

1. Cotangent Laplacian의 한계

해당 연산은 Mesh가 manifold여야 하고, 삼각형의 모양이 너무 찌그러지면 안됩니다. 논문에서는 이를 해결하기 위해서 isotropic explicit remeshing(삼각형의 크기와 모양을 균등하게 리샘플링)하고 manifold preprocessing(mesh를 매끄럽고 연속적인 구조로 미리 정리)하는 방식을 사용했습니다. 이는 기존 MeshUP가 TextDeformer에서도 발견된 문제입니다.

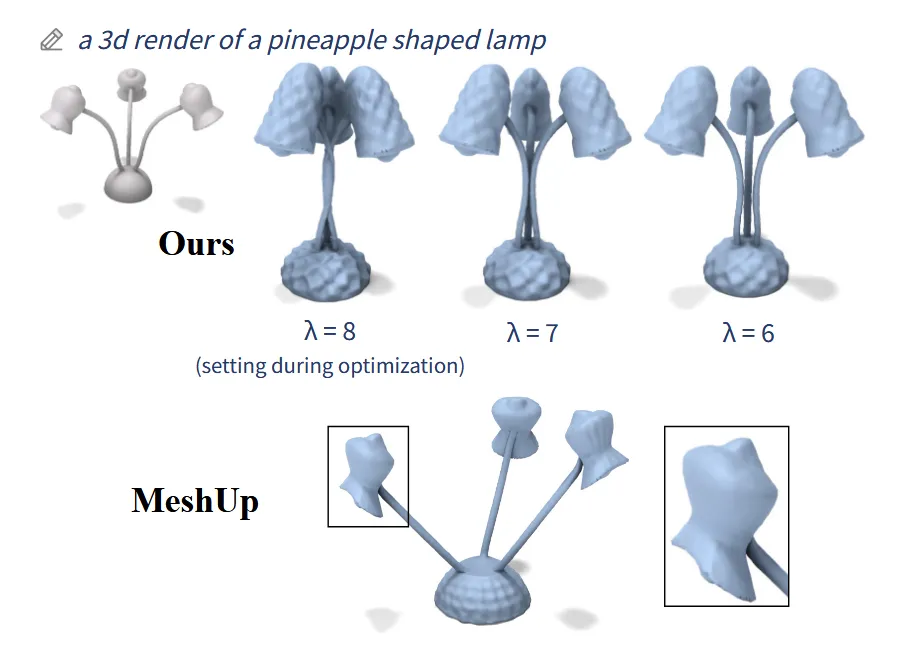
2. Self-intersection

어떤 스타일 변형에서는 mesh의 일부가 자기 자신과 겹치는 현상(self-intersection)이 생길 수 있습니다. 위의 그림을 보면 램프의 막대들이 중심을 향해 회전하면서 서로 관통해버렸습니다. 이럴 때는 λ값을 유동적으로 변경하면 됩니다.