Mip-NeRF: A Multiscale Representation for Anti-Aliasing Neural Radiance Fields 논문리뷰

논문링크

https://arxiv.org/pdf/2103.13415

Abstact

NeRF 모델에서 training과 testing과정에서 다른 해상도의 이미지를 사용할 경우 흐릿해지거나 aliased 현상이 발생한다.

하나의 픽셀에 대해서 여러개의 ray를 사용하는 supersampling방법으로 이를 해결할 수 있지만 이는 비효율적이다.

따라서 우리는 mip-NeRF라는 continuously-valued scale을 이용해서 이를 해결할 것이다.

NeRF보다 7% 빠르고, 평균 에러 비율은 17%감소, 멀티스케일 변형에서는 60%까지 에러 비율을 감소시킨다.

Introductioin

NeRF의 한계

blurring

PE를 통해서 고차원으로 임베딩 시켰지만, 샘플링 해상도가 고정적이므로 high frequency 성분을 포함하는 텍스처나 경계 부분이 부드럽게 표현되면서, 전체 이미지가 뭉개진 듯한 효과가 나타난다. 주로 close-up(가까운) view에서 발생한다.

Aliasing

위에서도 말했지만, 고정된 해상도에서 샘플링을 수행하기 때문에, 먼 거리나 작은 물체의 경우 충분한 샘플링 밀도를 확보하지 못합니다. 이에 세밀한 패턴을 제대로 표현하지 못하게 하여, 계단 현상이나 깜빡임과 같은 Aliasing 현상이 나타난다. 주로 distant(멀리 떨어진) view에서 발생한다.

해결책

offline raytracing

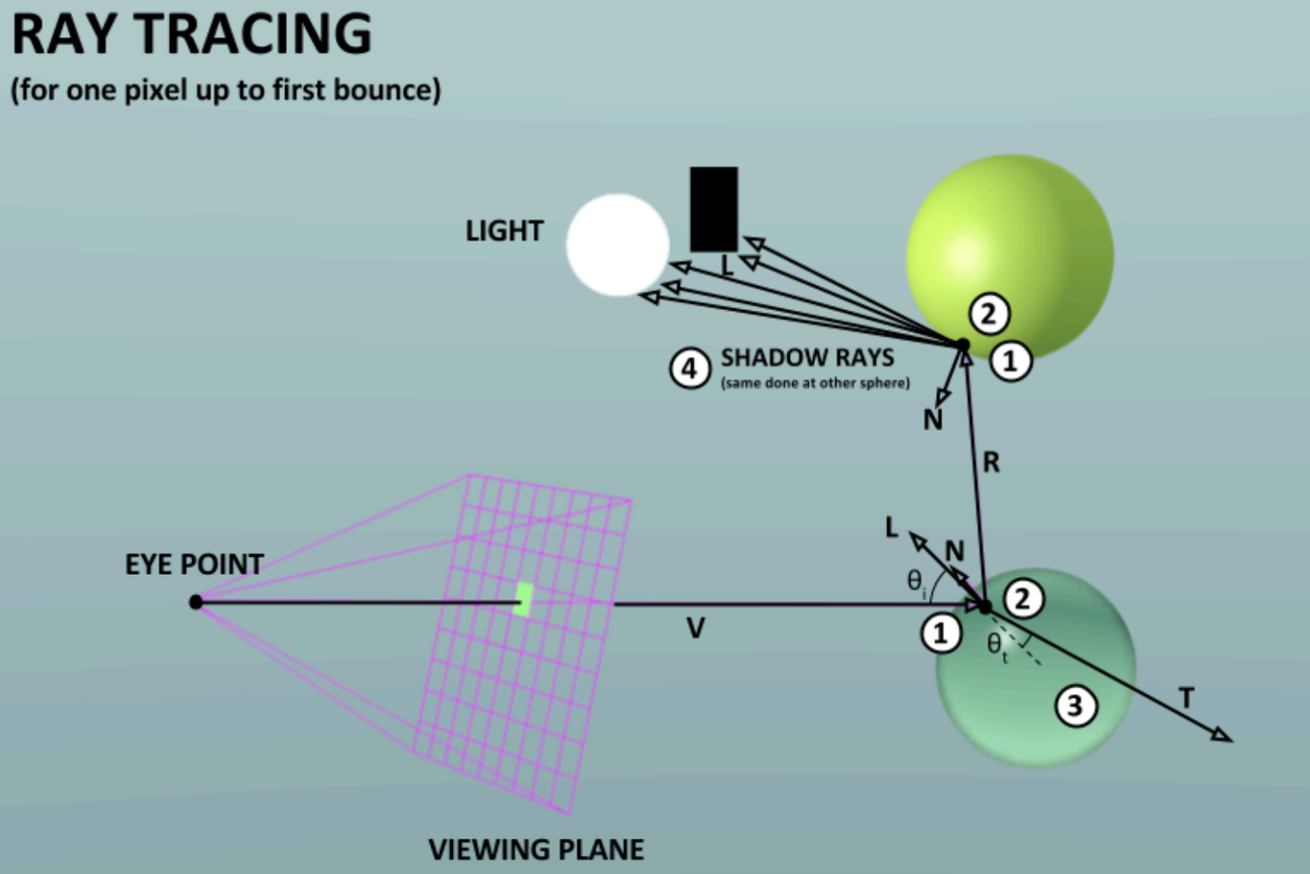
광선이 장면을 탐색하고 물체와 상호작용하는 방식을 시물레이션하여 매우 사실적인 이미지를 생성하는 과정이다. 성능이 매우 좋지만 수백번의 MLP계산을 하는 NeRF에서 사용하기에는 너무 많은 계산이 필요하다.

mipmapping

screen의 다양한 해상도에대해서 texture의 다양한 해상도를 미리 만들어 놓은 것. 이러한 방식은 pre-filtering이라고 불린다.

기존에는 카메라에서부터 하나의 픽셀까지의 ray에대해서 점을 샘플링할 때 점은 말 그대로 하나의 점이었다. 하지만 다양한 해상도를 고려하는 Mip-NeRF에서는 이 점이 하나의 원이 되고 픽셀에 가까워질수록 원은 커진다. 이러한 형태를 conical frustum이라고 정의한다.

추가적으로 원이 커지면 저해상도, 작아지면 고해상도인 이유에 대해서 간단히 설명하겠다. 원의 크기가 커진다는 것은 더 넓은 영역을 샘플링하기때문에 여러 픽셀의 정보를 통합하여 평균적인 값을 계산하는 과정이다. 이는 전체적인 정보를 제공하므로 저해상도의 정보를 갖는다.

Conical frustum 내의 샘플링 포인트들은 Gaussian 분포로 통합된다.원의 중심은 Gaussian분포의 평균, 원의 크기는 Gaussian분포의 공분산 행렬로 변환된다. Gaussian분포로 바꾸는 이유는 샘플링 영역을 더 정확하고 통합적으로 표현하기 위해서라고 나와있다(자세히는 이해가 안됐지만 Positioinal Encoding을 추가하기 위함이지 않을까라는 개인적인 의견).

추가적으로 NeRF의 optimizing 방법 중 hierarchical sampling에서 ‘coarse’와 ‘fine’의 MLP가 분리되어있었지만, Mip-NeRF에서는 하나로 합쳤다.

Related Work

이전에 나왔던 해결책으로 supersampling을 사용한 연구들이 나왔지만 위에서 말한 것처럼 cost측면에서 적절하지 않다.

따라서 Prefiltering 방법을 사용해서 lowpass-filtered를 사용해 고주파수 성분을 줄이도록 한다.

다양한 원이 다양한 해상도를 갖는 것을 알기 때문에, 미리 다양한 원을 갖는 conical frustum은 준비해두고 이에 대해서 우리가 샘플링할 부분만 가져와서 사용하면된다.

Mip-NeRF에서의 prefiltering 방법

장면의 기하학적 정보는 학습을 통해 아는 것이지 사전에 미리아는 정보가 아니기때문에 다양한 해상도의 표현을 사전에 계산해두는 것이 불가능하다. 따라서 prefiltering 방법을 training동안에 학습해야한다. 여기서 말하는 prefiltering 방법은 카메라에서의 반경(r1)과 픽셀에서의 반경(r2)에 대해서의 값을 학습해서 sampling하는 점에서의 반경을 바꾸도록 학습하는 것이다.

그리고 ray에 있는 각 점들은 연속적이기때문에 고정된 몇가지 해상도가 아닌, 임의의 해상도에서 장면을 학습한다. 즉 Continuous scale에 대해서 표현이 가능하고 이중 임의의 점에서 학습을 진행

Method

Cone Tracing

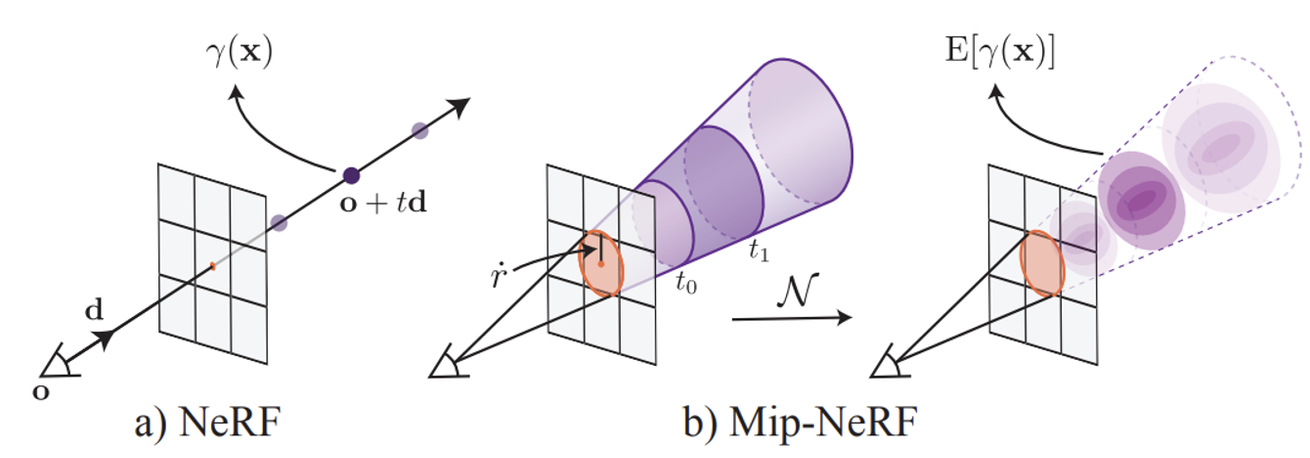
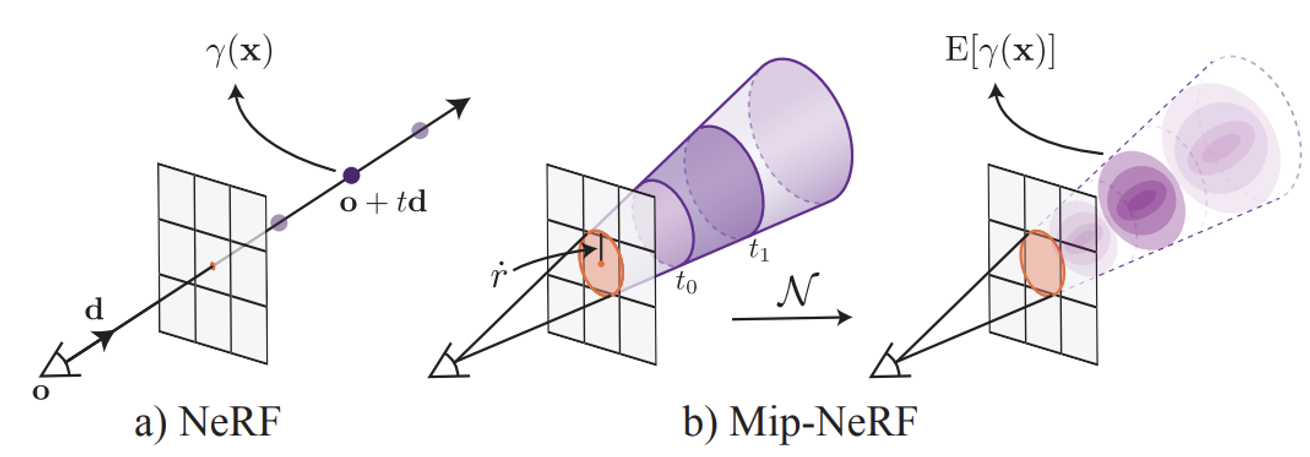
1. NeRF와 동일하게 카메라의 중심 o에서 픽셀의 중심을 통과하는 방향 d로 원뿔을 투사한다.
   
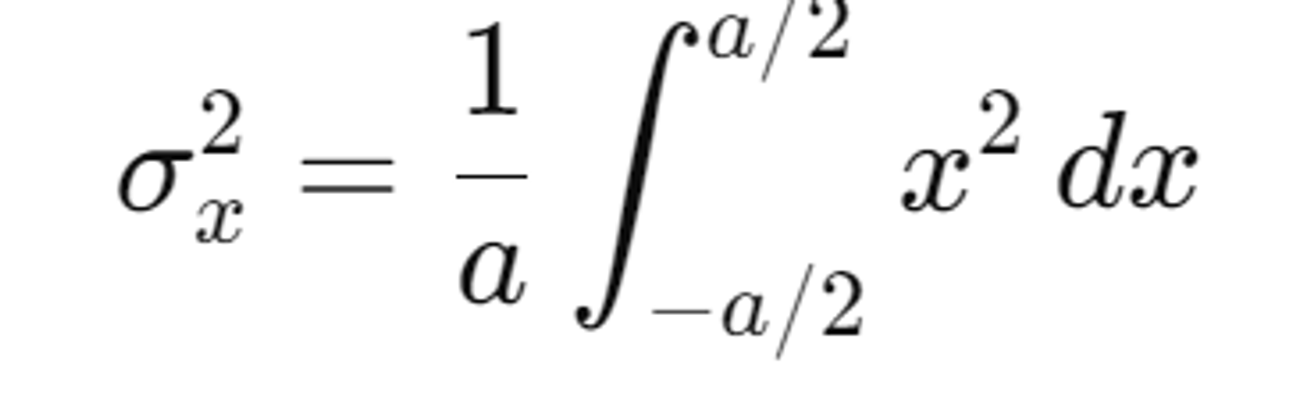
2. 이미지 평면에서의 반경 r’은 Wold 좌표계에서의 픽셀의 너비를 기준으로 $\frac{2}{\sqrt{12}}$로 스케일링하여 설정한다. 이는 픽셀의 분산과 일치하는 원뿔 단면을 생성한다.
   스케일링값이 $\frac{2}{\sqrt{12}}$인 이유는 우선 $x^2$(픽셀의 너비, 높이의 곱)을 중심에서 각 지점까지의 거리(a/2)로 적분을 하면 분산을 1/12로 알 수 있고, 2를 곱해주는 이유는 원뿔의 단면적이 픽셀의 면적과 정확히 일치하도록 설정하기 위해서(정확히 몰라도된다)
   
3. 특정 t값의 범위 내에서 원뿔의 위치를 정의하여 샘플링 영역을 설정한다.

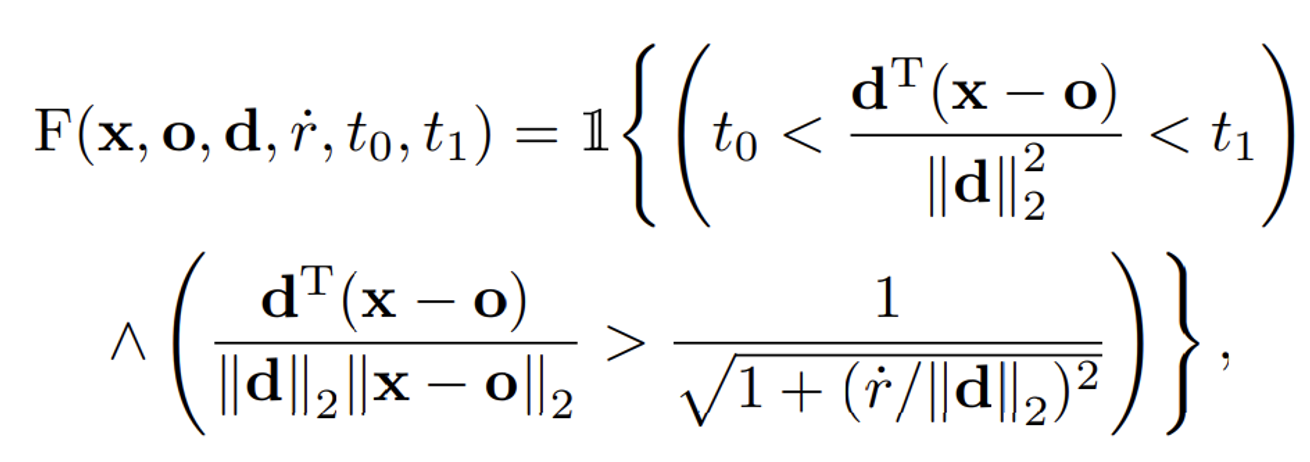
구성요소

• x: 검사하려는 3차원 점의 위치.
• o: 원뿔의 정점 (카메라의 중심).
• d: 원뿔의 축 방향 벡터 (광선의 방향).
• r˙: 원뿔의 반경, 픽셀의 너비를 기반으로 설정됨.
• t0와 t1: 원뿔의 시작과 끝을 정의하는 두 값.
• 1{⋅}: 조건이 참이면 1, 거짓이면 0을 반환하는 지표 함수.

수식

점 x가 원뿔의 축을 따라 t0와 t1사이의 범위에 위치하는지를 검사

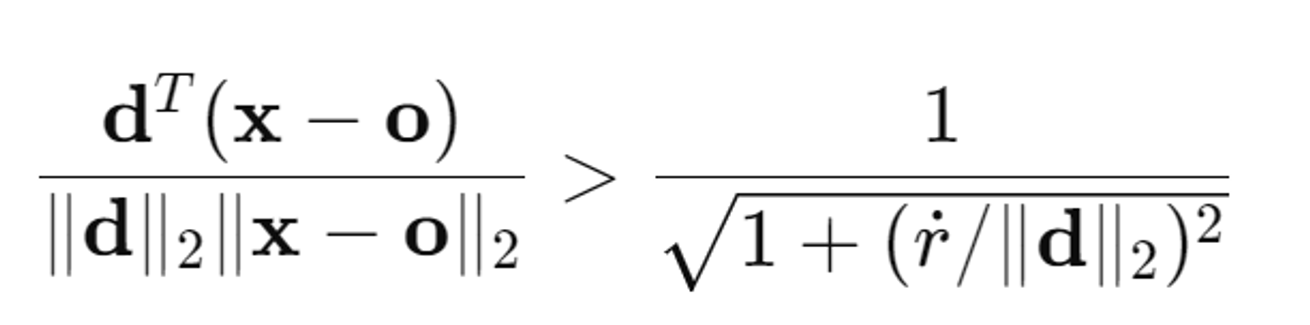
왼쪽의 수식은 벡터 d와 x-0간의 코사인 각도이다.

오른쪽의 수식은 원뿔의 각도에 따라 달라지는 임계값이다. 반경과 높이의 비율이 클수록 원뿔의 각도가 넓어진다, 즉 오른쪽 수식의 값은 원뿔의 코사인 각도이다.(아래 사진 참조)

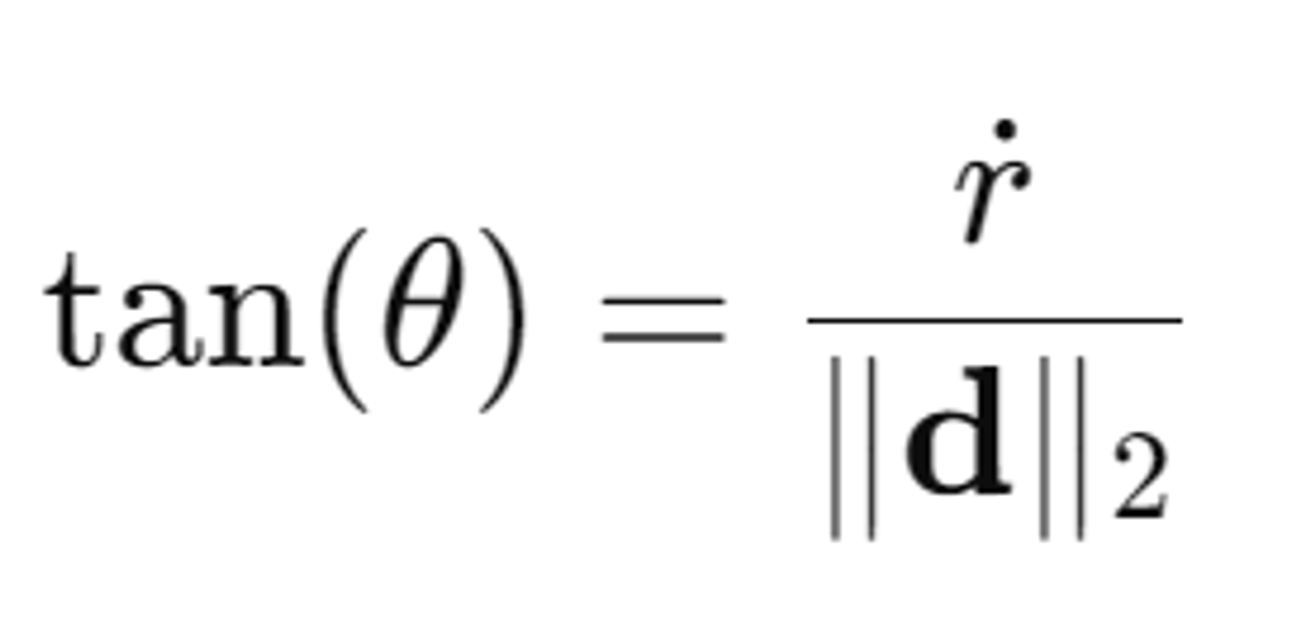
결국 이 조건은 점 x가 원뿔 내부에 있는지 여부를 확인하기 위한 것이다. 이 조건이 모두 만족되면, 수식 $F(\mathbf{x}, \mathbf{o}, \mathbf{d}, \dot{r}, t_0, t_1)$는 1을 반환하고, 그렇지 않으면 0을 반환

Integrated Positional Encoding

NeRF에서도 나왔듯이 PE를 추가한 효과는 굉장하다. 따라서 Mip-NeRF에서도 동일하게 추가할것이지만 현재의 값은 conical frustum이기때문에 이에 적적하게 추가해야한다.

conical frustum에 적절한 PE를 IPE(integrated positional encoding)라고 명명했다.

IPE를 적용하기 위해 수학적 편의를 고려해서 conical frustum을 가우시안 분포로 변경한다. (자세한 수식은 Appendix 참조)

midpoint: tµ = (t0 + t1)/2 and half-width: tδ = (t1 − t0)/2

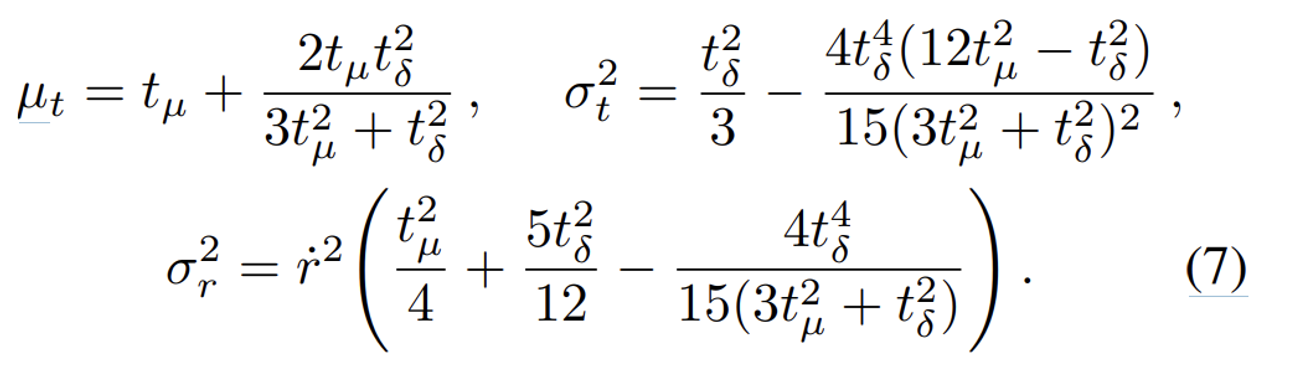
• 평균 거리 ( μt ): 원뿔의 축을 따라 위치하는 평균 거리
• 축을 따라 변하는 분산 ( $\sigma_t^2$): 원뿔의 축을 따라 변하는 거리의 분산
• 축에 수직인 방향으로 변하는 분산 ( $\sigma_r^2$ ): 원뿔의 단면 반경의 분산

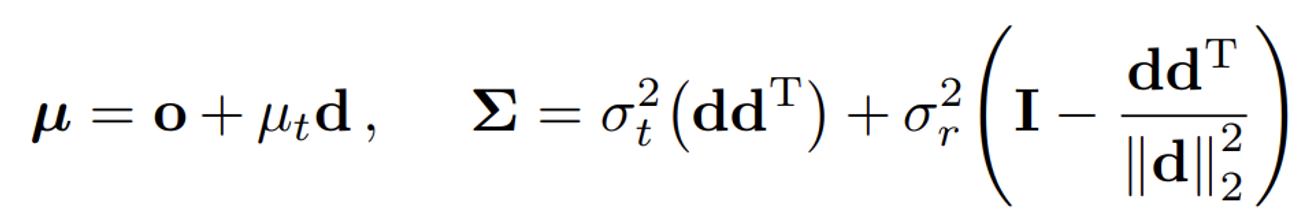
최종적으로 위와 같은 형태의 평균과, 분산을 얻는다.

IPE를 적용하기 위해 우선 PE를 Fourier feature로 변환한다.

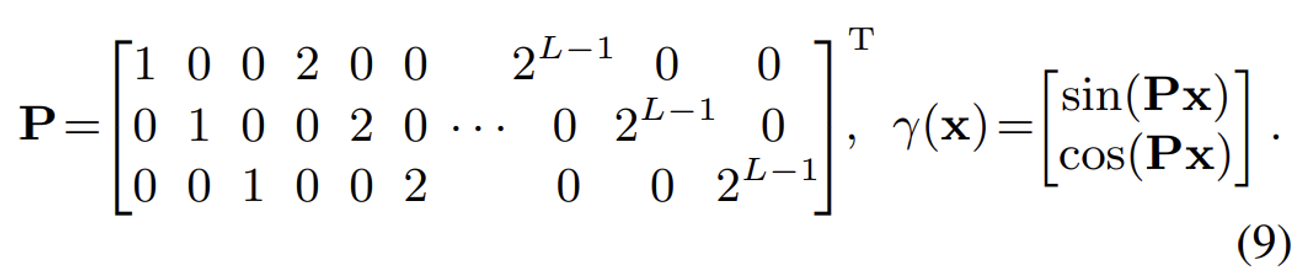
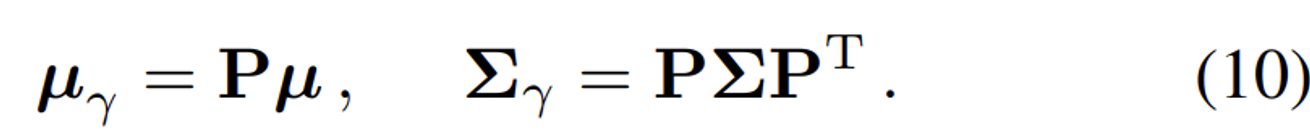
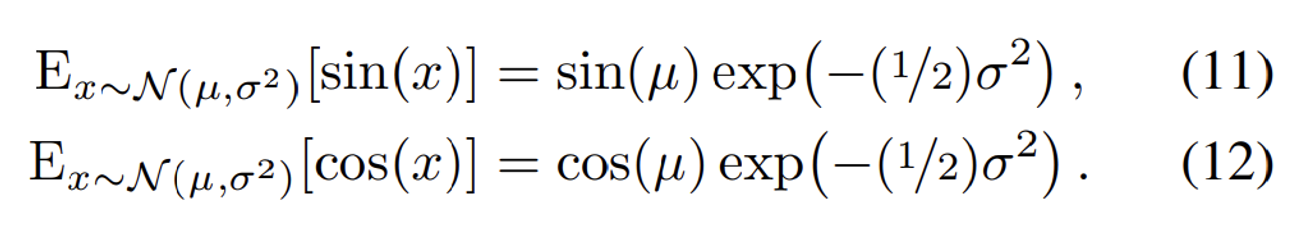
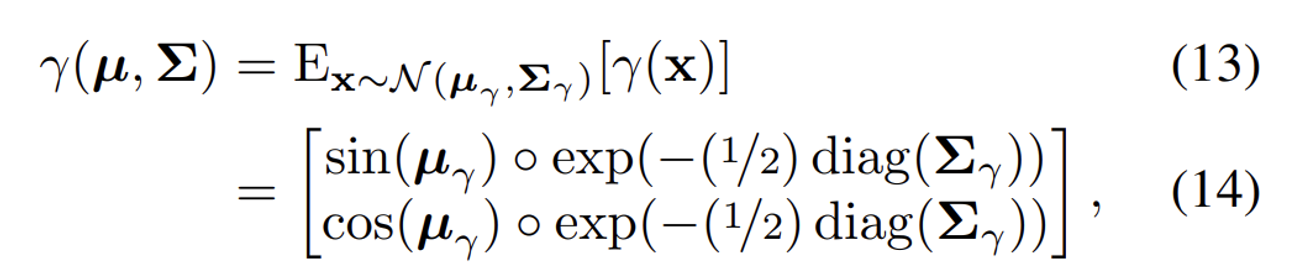
Gaussian의 평균과 공분산을 PE 공간으로 변환한 형태는 위와 같다. 마찬가지로 수식에 대한 부분은 따로 찾아보면 좋을거 같다.

결론만 말하자면 가우시안 분포의 평균과 분산에 대해서 각각 PE를 취하는 방식이 IPE라고 보면된다.

추가 수식

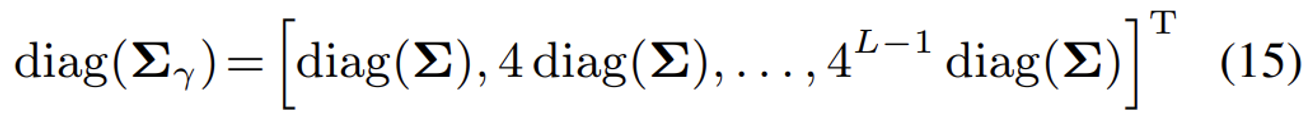
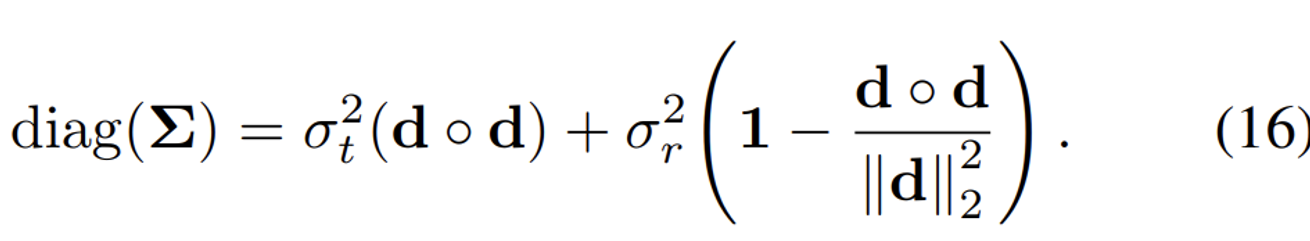
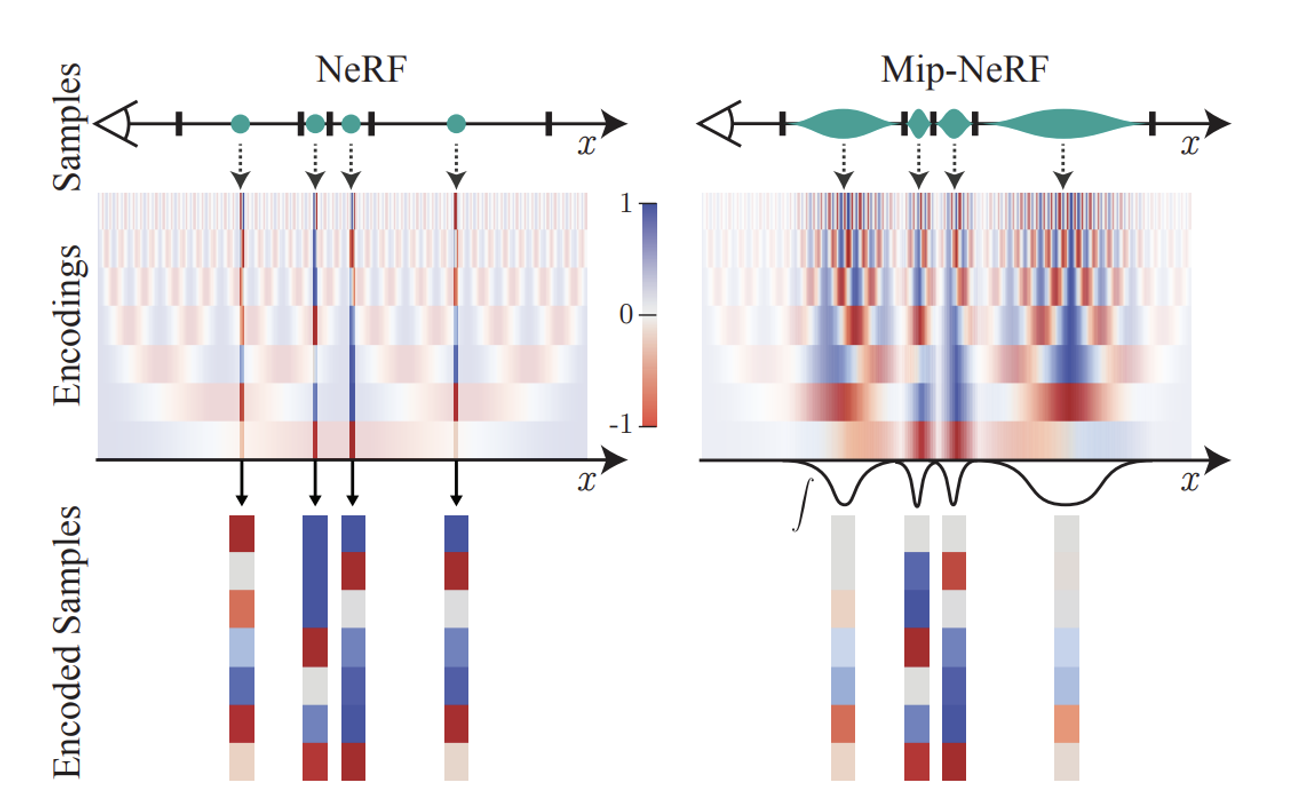
위의 사진은 1차원에서의 PE와 IPE의 차이를 보여준다.

사진에서 초록색 부분이 구간의 너비, 주파수가 Encoding에서 나타나는 빨간색 파란색 회색의 패턴들.

1. 주파수와 주기의 관계

PE의 경우:

• PE는 입력 좌표에 대해 주파수 성분을 추가하여 신호를 확장
• 여기서 각 주파수 성분은 특정 주기를 가진다. 예를 들어, 주파수가 높을수록 주기는 짧아진다.

IPE의 경우:

• IPE는 PE와 달리, 주파수가 특정 구간(interval)의 너비보다 큰 경우에는 주파수 성분이 영향을 받지 않는다.
• 반면, 주파수가 구간의 너비보다 작은 경우, 해당 주파수 성분은 구간 내에서 여러 번 진동하게 되므로, 그 주파수 성분이 감소된다.

2. 직관적인 설명

PE의 경우:

• 모든 주파수 성분을 보존
• 주파수 성분의 상한은 수동으로 조정되는 하이퍼파라미터 L에 의해 결정

IPE의 경우:

• 구간 내에서 일정한 주파수는 보존
• 구간 내에서 변하는 주파수는 부드럽게 제거
• 이는 각 사인(sine) 및 코사인(cosine) 성분을 조정하여 이루어진다.

3. IPE의 장점

• Anti-aliasing: IPE는 효과적으로 앨리어싱을 방지한다. 이는 변하는 주파수를 부드럽게 제거하고, 일정한 주파수를 보존하기 때문
• 자동 조정: IPE는 L을 매우 큰 값으로 설정하고 조정할 필요 없이 사용할 수 있다.

Architecture

하나의 coarse & fine Network

NeRF모델에서는 PE가 단일 스케일에서만(하나의 점에서만) 작동하기 때문에 coarse와 fine 네트워크가 필요했다. coarse 네트워크는 대략적인 장면을 모델링하고, fine 네트워크는 세부사항을 모델링 했다.

하지만 Mip-NeRF는 conical frustum과 IPE를 사용하기 때문에 멀티 스케일 정보를 이용하므로 단일 MLP가 여러 스케일에서의 정보를 학습할 수 있다.

→ 모델 사이즈가 반으로 줄고, 렌더링이 정확해지고, 샘플링이 효율적이고, 알고리즘이 단순해진다.

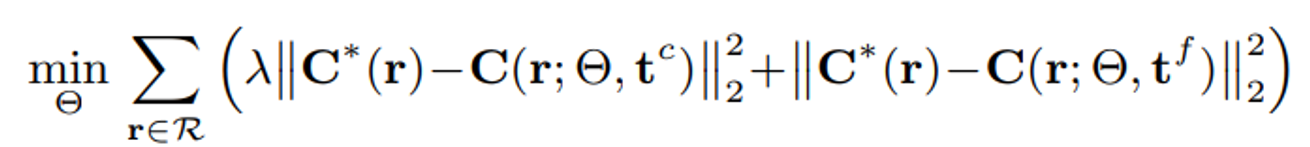
[NeRF] coarse samples: 64 & fine samples:128

[Mip-NeRF] coarse samples: 128 & fine samples:128

추가적으로 coarse sample의 결과에 대한 가중치 부분도 수정했다

가중치 w를 부드럽고 연속적인 분포로 만들어 샘플링의 안정성을 높이고, 빈 공간에서도 최소한의 샘플이 선택되도록 한다.

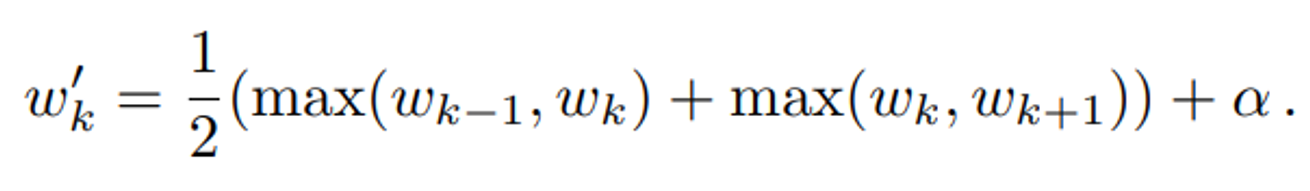
• 2-tap max filter로 가중치 값을 최대값으로 대체 → 큰 가중치 값이 인접하면 큰 값으로 대체되므로, 강한 특징이 더욱 두드러 진다.
  
• 2-tap blur filter로 가중치 값을 주변 값과 평균화
• 하이퍼파라미터 α를 더해 빈 공간에서도 샘플이 선택되도록 한다.
• 가중치 값을 다시 정규화하여 합이 1이 되도록 한다.

Results

dataset: Blender(NeRF에서 사용한 데이터)

해당 데이터의 focal lenght과 해상도 그리고 물체와의 거리가 모두 동일하기 때문에 실제 데이터보다는 상당히 쉽게 학습이 가능하다.

따라서 NeRF의 한계를 나타내기 위해서 Multiscale Blender dataset을 이용했다.

• Downsampling: 원래의 Blender dataset의 각 이미지를 다음과 같이 다운샘플링:
  • 원래 이미지 크기에서 1/2 (factor of 2)
  • 원래 이미지 크기에서 1/4 (factor of 4)
  • 원래 이미지 크기에서 1/8 (factor of 8)
• Camera Intrinsics 수정: 다운샘플링된 이미지들에 맞추어 카메라 내부 파라미터(intrinsics)를 수정
• Dataset 통합: 원래 이미지들과 세 가지 다운샘플링된 이미지를 하나의 데이터셋으로 결합

추가적으로 Mip-NeRF를 multiscale Blender 데이터셋에서 학습할 때, 각 픽셀의 손실(loss)을 원본 이미지에서 그 픽셀의 면적으로 스케일링한다. 이렇게 하는 이유는 저해상도 이미지의 적은 수의 픽셀이 고해상도 이미지의 많은 수의 픽셀과 비교하여 동일한 영향을 미치도록 하기 위함이다.

예를들어 1/2 해상도 이미지의 픽셀: 원래 이미지에서 픽셀 면적의 1/4이므로 손실을 4배로 스케일링

3가지 평가지표

PSNR(Peak Signal-to-Noise Ratio)

원본 이미지와 압축된 이미지 또는 변환된 이미지 간의 품질을 비교(단위: dB, 클수록 좋다)

계산 방법

1. 두 이미지 간의 Mean Squared Error (MSE)를 계산합니다.
   • MSE는 두 이미지 간의 각 픽셀 차이를 제곱하여 평균을 낸 값입니다.
   • ${MSE} = \frac{1}{N} \sum_{i=1}^N (I_{i} - K_{i})^2$
2. PSNR을 계산합니다.
   • ${PSNR} = 10 \log_{10} \left( \frac{\text{MAX}^2}{\text{MSE}} \right)$
   • 여기서 MAX는 이미지의 최대 픽셀 값입니다 (예: 8비트 이미지는 255).

SSIM(Structural Similarity Index)

두 이미지 간의 구조적 유사성을 측정하는 지표. SSIM 값은 -1에서 1 사이이며, 1에 가까울수록 두 이미지가 유사하다.

계산 방법

SSIM은 세 가지 요소를 결합하여 계산:

1. 밝기(luminance) 비교
   • 두 이미지의 평균 밝기 비교
   • $l(x, y) = \frac{2\mu_x \mu_y + C_1}{\mu_x^2 + \mu_y^2 + C_1}$
2. 명암 대비(contrast) 비교
   • 두 이미지의 표준 편차 비교
   • $c(x, y) = \frac{2\sigma_x \sigma_y + C_2}{\sigma_x^2 + \sigma_y^2 + C_2}$
3. 구조(structure) 비교
   • 두 이미지의 공분산 비교
   • $s(x, y) = \frac{\sigma_{xy} + C_3}{\sigma_x \sigma_y + C_3}$

SSIM(x,y)=l(x,y)⋅c(x,y)⋅s(x,y)

LPIPS(Learned Perceptual Image Patch Similarity)

두 이미지 간의 유사성을 측정하는 지표.LPIPS 값은 낮을수록 두 이미지가 유사하다는 것을 의미

계산 방법

사전 학습된 신경망 (예: VGG, AlexNet)에서 두 이미지의 특징 맵을 추출

추출된 특징 맵 간의 거리를 계산

가중치를 적용하여 두 이미지 간의 유사성을 측정

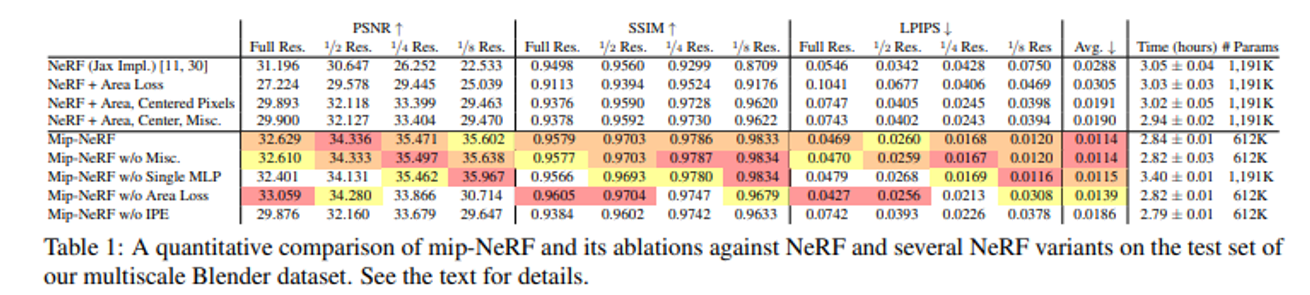
NeRF가 blender dataset의 SoTA이기때문에 NeRF와 해당 모델을 변형한 모델들과의 비교만 진행

w/o Misc: removes those small changes(뜻을 몰라서 논문의 원본 내용을 가져왔다.)

w/o Sinlge MLP: NeRF처럼 2개의 MLP를 사용했을 때의 결과

w/o Area Loss: 해상도를 변경했을 때 loss도 똑같이 변경안하는 경우

w/o IPE: IPE방식이 아닌 PE방식을 사용한 경우

Multi-sacle에서도 당연히 성능이 좋았고, single-scale에 대해서도 NeRF보다 성능이 좋았다.

추가적으로 Introduction에 나온 Supersampling방식을 이용해서도 성능 비교를 했는데 성능의 큰 차이는 없지만 시간적인 측면이 매우 다르다는 것을 알 수 있다.

Conclusion

결론적으로 NeRF에 비해서 multi-scale resolution 성능 뿐만아니라, single-scale과 시간 단축까지 성공한 Mip-NeRF모델이다. 해당 모델을 기반으로 나온 Mip-NeRF 360도 추후에 업로드 하겠다.