Mip-Splatting: Alias-free 3D Gaussian Splatting 논문 리뷰

프로젝트 링크

https://niujinshuchong.github.io/mip-splatting/

논문링크

https://drive.google.com/file/d/1Q7KgGbynzcIEyFJV1I17HgrYz6xrOwRJ/view

Summary

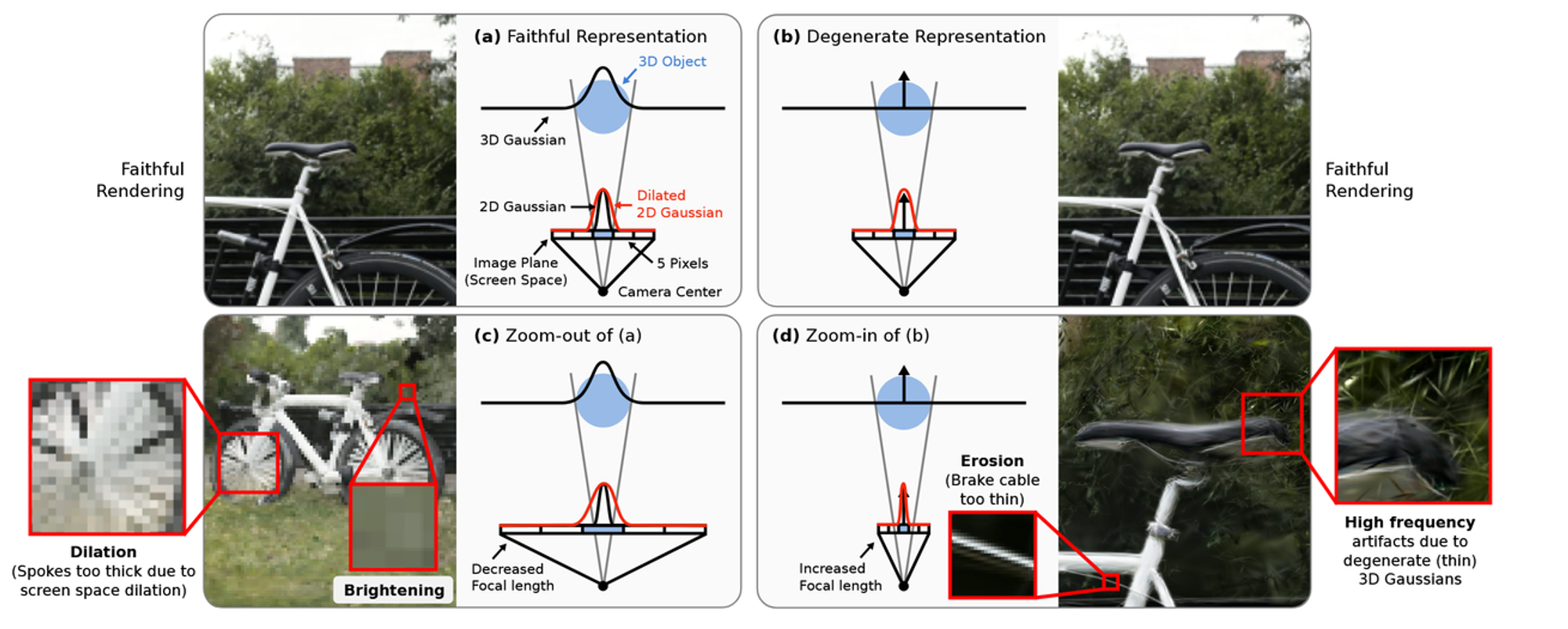
기존 3D Gaussian Splatting에서 2가지 부분의 코드만 바꿈으로써 Aliasing 문제를 해결했습니다.

(b)를 보면 Gaussian이 너무 작게 보여서 직선의 형태로 보여진다고 나타나 있는 그림 이고,

(c)를 보면 Zoom-out을 했기 때문에 많은 확장을 해서 깨지는 현상입니다. 예를들어 바퀴의 디테일을 표현하지 못합니다.

(d)는 Zoom-in을 했기 때문에 적은 확장을 해서 high frequency문제가 발생하는 현상입니다. 예를들어 브레이크 선이 너무 얇게 나타나는 현상과 높은 주파수의 artifact가 보이는 현상입니다.

3D Smoothing Filter

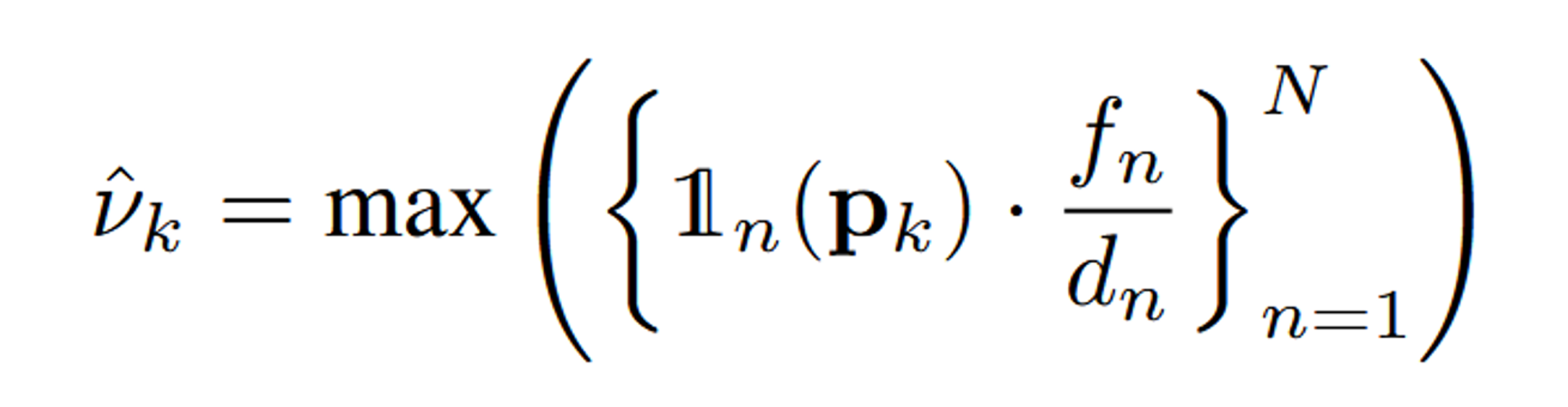
Nyquist’s theorem 이론에 따르면, 샘플링 주파수가 최대 주파수 신호의 2배이상이어야지 신호를 적절하게 변환할 수 있기때문에 최대 주파수를 제한하는 것입니다. 이때 최대 주파수는 여러가지 뷰에서 본 카메라를 기반으로 나타냅니다.

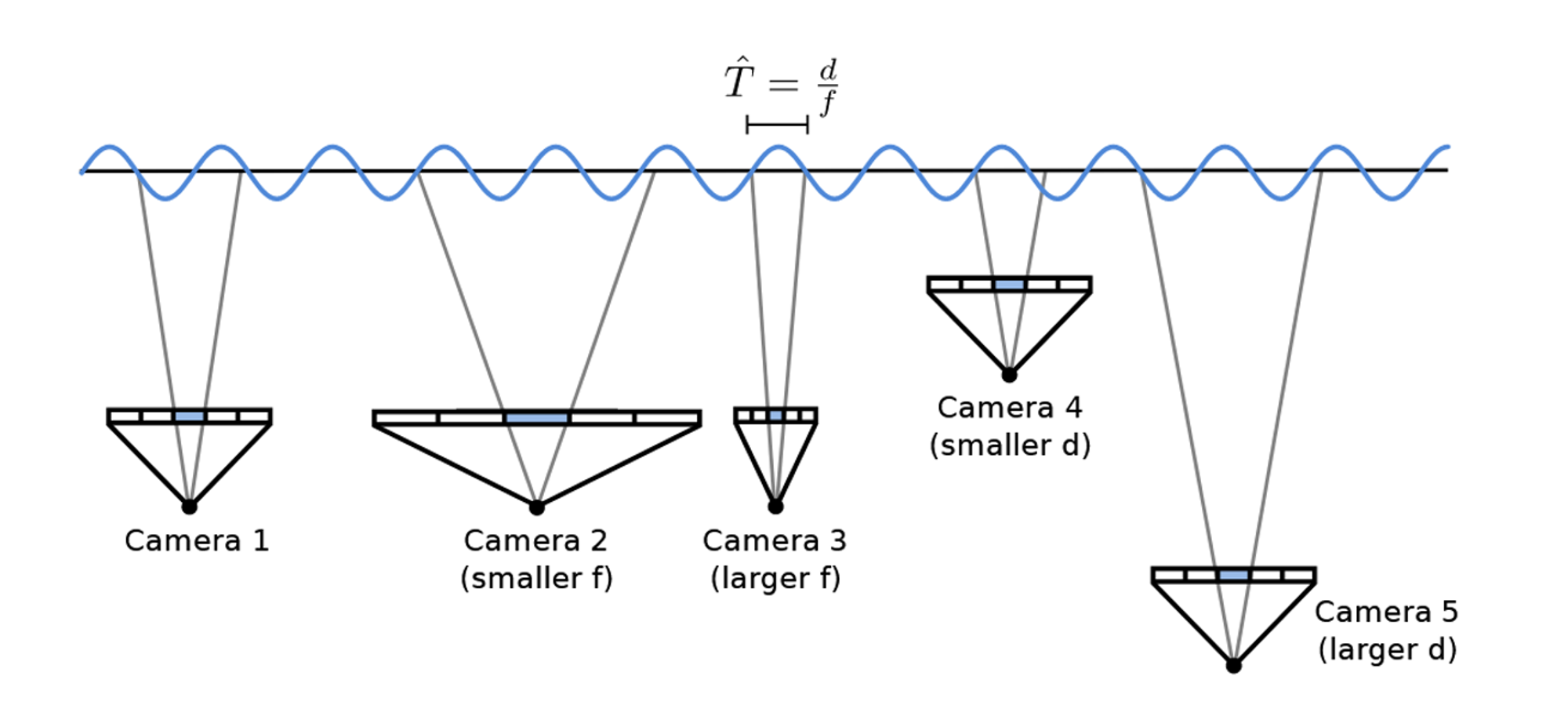
2가지 요소가 영향을 미치는데 카메라에서 gaussian의 중심까지의 거리 d와, focal lenght인 f입니다.

f값은 망원경 거리라고 생각하면 길어지면 더 좁은 범위를 자세히 봅니다. 따라서 샘플링 간격을 작게해서 세부적인 내용을 파악해야됩니다.

d값은 클수록 더 멀리 떨어져서 넓은 시야를 보게 됩니다. 따라서 샘플링 간격을 크게해서 global한 내용을 파악해야합니다.

Gaussian low-pass filter

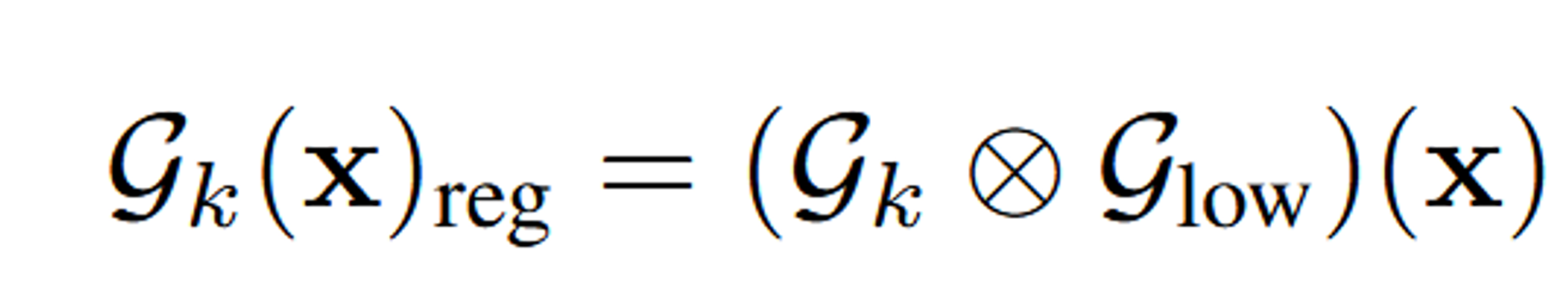
위의 과정을 통해서 최대 샘플링 주파수를 고정시키고, Guassian Low-Pass filter를 적용시켜서 고주파 성분을 제거합니다. 쉽게 고주파 성분을 제거하기 위해 low-pass filter를 convolution 연산해준다고 생각하면됩니다.

2D Mip filter

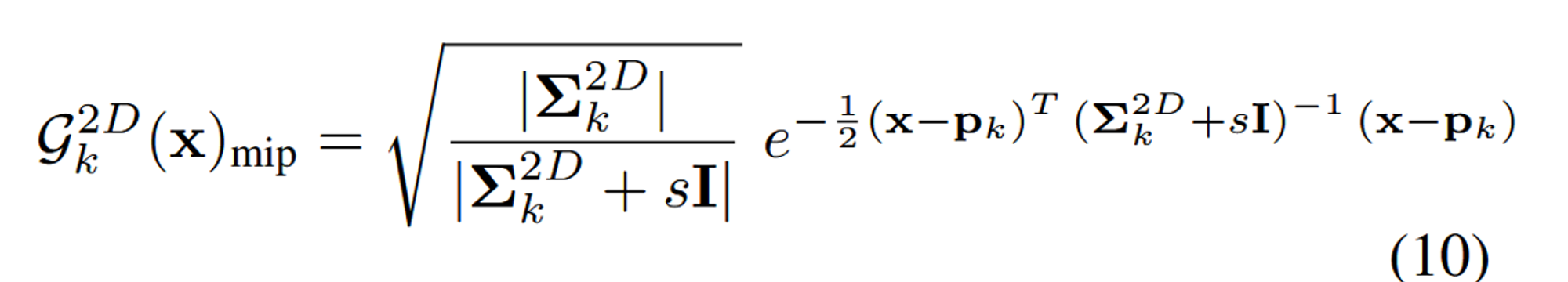
2D Mip Filter를 통해서 샘플링 속도가 낮아지면서 발생하는 aliasing 문제를 해결했습니다. 기존 3DGS에서 사용되는 dilation은 단순 확장이기때문에 특정 샘플링 비율에서만 효과적이었지만, 픽셀 안에 있는 모든 빛을 동일하게 더하는 방식을 사용하는 2D Mip filter를 사용해서 모든 샘플링 비율에서 효과적인 방식을 나타냈습니다.

결과적으로 artifact문제를 해결하게 됐습니다.

이 논문자체가 수식 위주다보니 상당히 어렵고 마지막에 나온 Limitation에서 결과적으로 zoom out 상황에서 오류가 발생하고, 최대 샘플링 비율을 계산하고 저장하는 과정에서의 비효율성이 존재한다고 하다보니 개인적으로 의문이 생기는 논문이었습니다.

Abstract

3D Gaussian Splatting의 등장으로 novel view synthesis 분야에서는 빠르고 좋은 결과를 낼 수 있었습니다. 하지만 Smapling rate의 변화(focal lenght, camera distance)가 artifact를 야기했습니다. 이는 3D frequency constraints의 부족과 2D dilation filter 때문에 발생하는 현상임을 찾았습니다. 이 문제를 해결하기 위해서 Mip-Splatting에서는 3D smoothing filter와 2D Mip filter를 이용했습니다.

Introduction

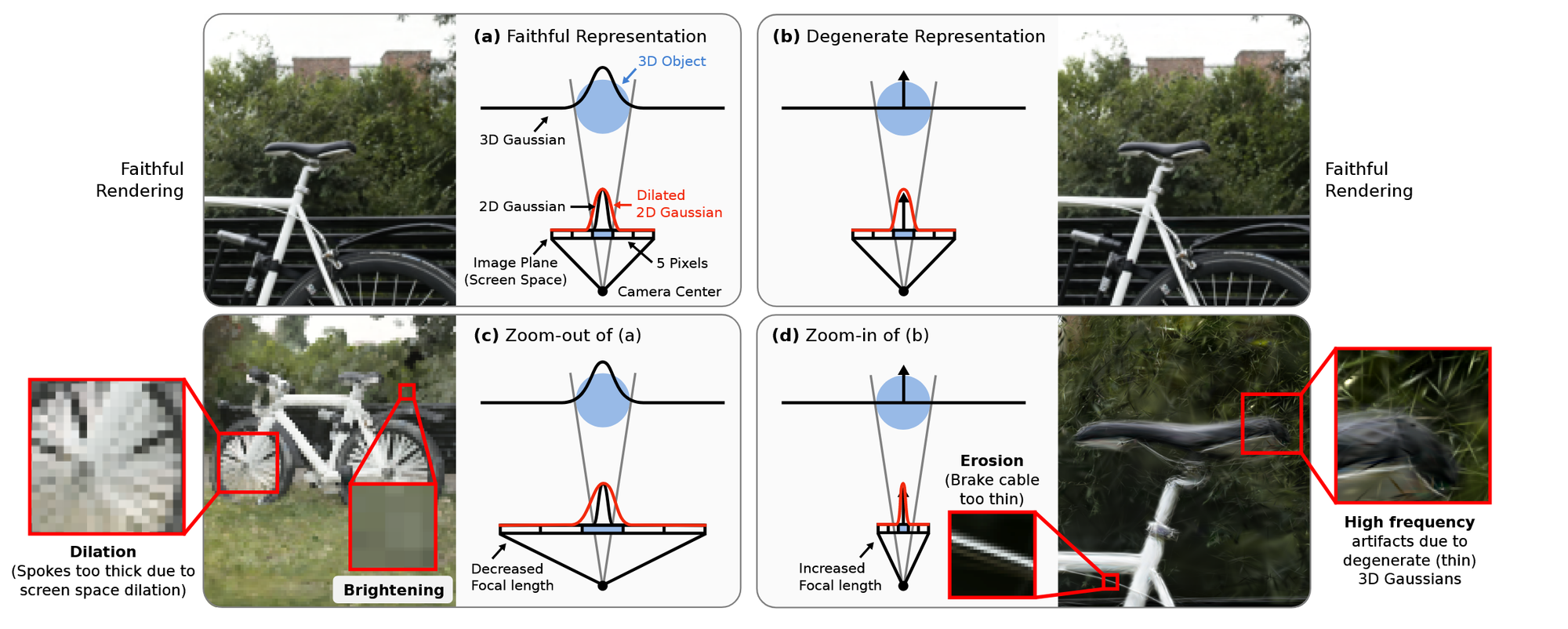
NVS(Novel View Synthesis)에서 NeRF에 이어 3D GS의 등장으로 효율적이고 좋은 성능을 낼 수 있었습니다. 하지만 위의 그림처럼 sampling rate의 변화에 따라서 artifact(인공적인 현상)이 나타납니다. 구체적으로 설명하면, zoom out을 하면 투영되는 2D Gaussian의 크기가 줄어들고 동일한 양의 dilation을 수행했을 때 dilation artifact를 야기합니다. (c)그림을 보면 이 자전거의 바퀴의 디테일들이 표현되지 못하는 것으로 이는 2D Gaussian의 크기가 작아져서 local적인 특징을 반영하지 못하는 현상입니다. 반대로 zoom in을 하면 2D Gaussian의 크기가 늘어나서 erosion 현상이 나타납니다. (d) 그림을 보면 브레이크 선이 너무 얇게 나타나거나, 높은 주파수의 artifact가 나타납니다.

이에 논문에서는 3D GS에서 조금의 코드 변화를 통해서 Sampling rate를 변화하더라도 위와 같은 artifact 현상들이 발생하지 않게 3D smoothing filter와 2D Mip filter를 도입하여서 문제를 해결했습니다.

Related Work

Novel View Synthesis

이전에 나온 내용이 반복돼서 생략하겠습니다.

Primitive-based Differentiable Rendering

Primitive-based Differentiable Rendering은 기하학적 Primitive(점, 구 등)를 이미지 평면에 rasterize하는 기술입니다. 3D Gaussian Splatting은 anisotropic 3D Gaussian을 사용하여 장면을 표현하며, tile-based sorting을 통해 렌더링 효율성을 높인 기술입니다. 하지만 이전에 설명한 문제 때문에 3D smoothing filter와 2D Mip filter를 도입했습니다.

Anti-aliasing in Rendering

Aliasing(계단 현상과 같은 잘못된 결과를 보이는 현상)을 해결하기 위해 2가지 방법이 제시됐습니다.

• Supersampling: sample의 개수를 늘리는 것
• prefiltering: 신호에 low-pass filtering을 적용하는 것

이 논문에서는 3D Space에서 band-limited filter를 적용하며, 필터 크기는 훈련 이미지에 의해 결정됩니다. 또한, 2D Mip filter는 3D Gaussian을 2D Gaussian low-pass filter로 대체합니다.

Preliminaries

Sampling Theorem

Sampling Theorem은 NyquistShannon Sampling Theorem이라고도 불리는데, 이는 연속적인 신호를 정확한 이산적인 신호로 변환해주는 방법입니다. 정보 손실 없이 이산적인 신호로 변환해 주기 위해서는 아래와 같은 2가지 조건을 만족해야 합니다.

• 조건1: band-limited, 즉 최고 주파수 v를 넘으면 안됩니다.
• 조건2: sampling rate $\hat{v}$ 가 연속 신호에서의 최고 주파수의 2배이 상이어야합니다.( $\hat{v}$ ≥ 2ν)

실제로 2조건을 만족시키기 위해서 low-pass나 anti-alising filter를 샘플링 이전에 적용시킵니다.

3D Gaussian Splatting

간략한 3DGS에 대한 설명을 하는 구절입니다.

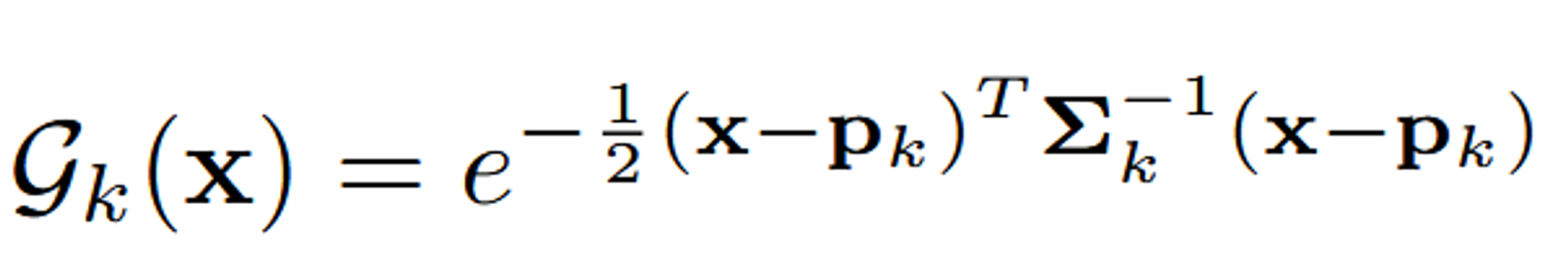
위의 수식은 3D 공간상에서 Gaussian을 표현하는 방법입니다.

• $p_k$: Gaussian의 중심
• $a_k$: (opactiy) 투명도를 나타내는 값
• $Σ_k$: 공분산(covariance) 행렬 (3x3) → $Σ_k = O_ks_ks^T_ kO^T_k$ (s: scaling vector, O: rotation matrix)

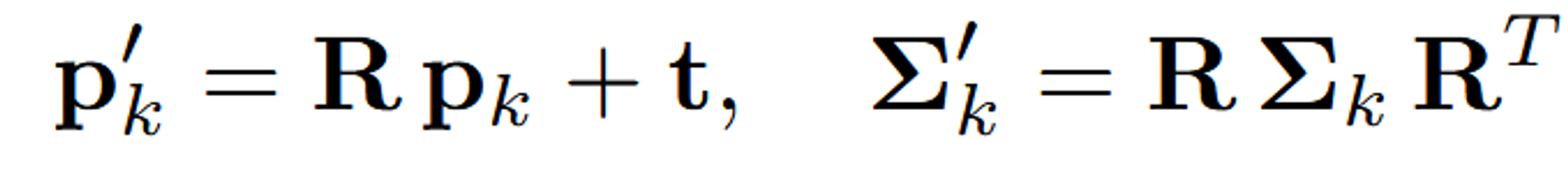
주어진 3D Gaussian 값을 2D Camera 좌표계로 Projection하는 과정입니다.

• R: Camera Rotation
• t: Camera translation

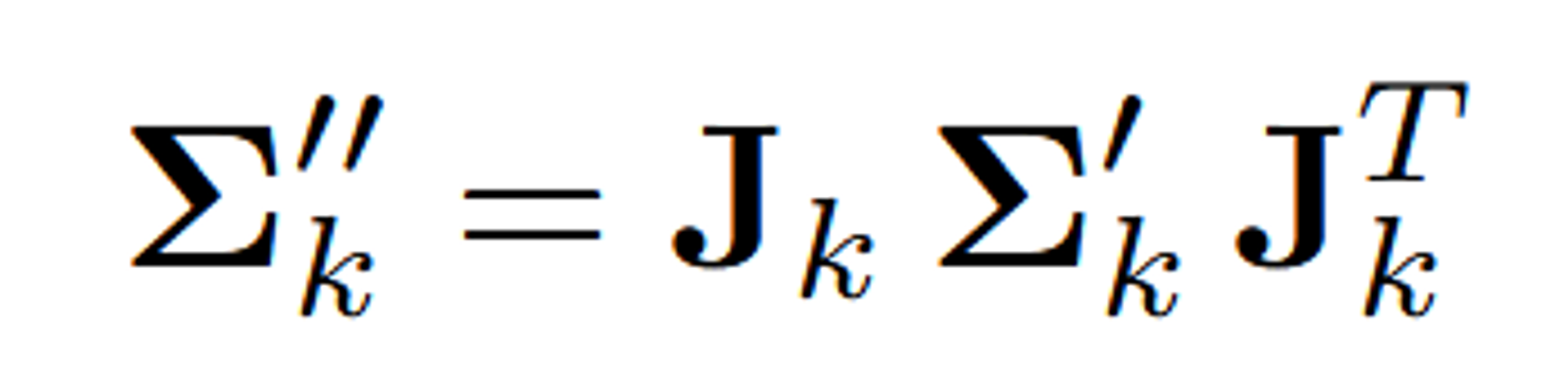
이후에 local affine transformation을 통해서 ray space로 projection 됩니다.

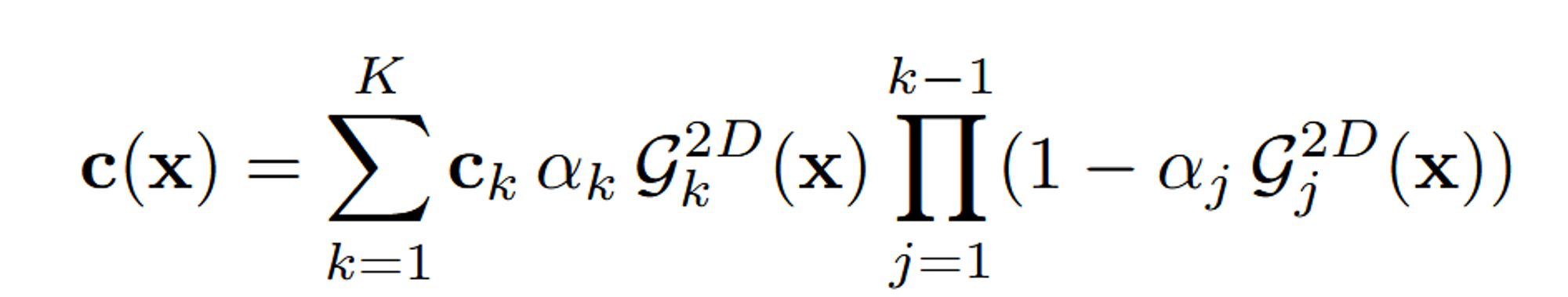
픽셀 x에서 최종적인 색깔은 위와 같이 alpha-blending 방식을 기반으로 이전 값들에 영향을 받으며 계산됩니다.

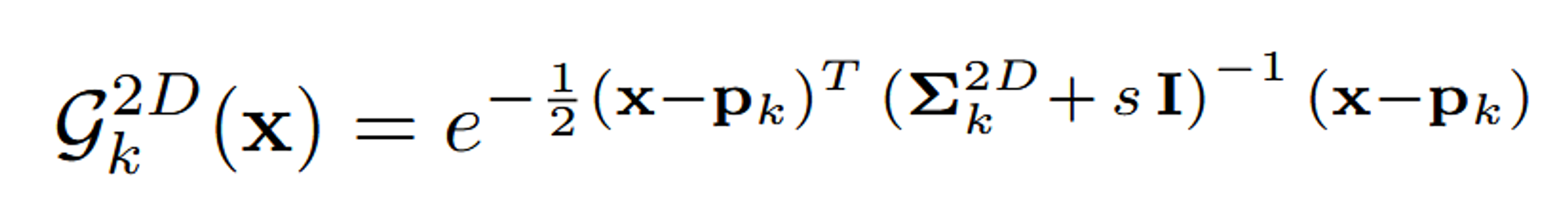
Dilation은 Gaussian의 크기가 픽셀보다 작은 경우 확장하는 것입니다.

Sensitivity to Sampling Rate

해당 그림을 이제 다시 한번 자세히 보도록 하겠습니다.

아래에 나와있는 2D space상에서 5개의 픽셀을 통해서 3D object를 관찰하고 있습니다.

(b)의 경우 Gaussian이 너무 작게 보여서 지금 위쪽에 불록 나오지 않고 선으로 잘못 표현되고 있고 심지어 직선처럼 보인다고 나타납니다. 이는 잘못된 표현 방식입니다.

(c)는 zoom-out을 했기 때문에 많은 확장을 해서 깨지는 현상

(d)는 zoom-in을 했기 때문에 적은 확장을 해서 high frequency 문제가 발생하는 현상입니다.

이러한 문제는 Dilation 즉 확장 때문에 발생하는 문제인데 단순히 확장을 제거하더라도 최적화 문제와, Aliasing 문제가 발생하기때문에 제거할 수 없습니다.

Mip Gaussian Splatting

3D Smoothing Filter

“Reconstruction된 3D Representation의 최고 frequency는 train view에 정의된 sampling rate에 의해 제한시킨다!”

아래 식이 장황하고 어려운데 한마디로 쉽게 정리하면 Nyquist’s theorem를 만족시키기 위해서 샘플링 주파수의 최대값을 고정시키는 것입니다.

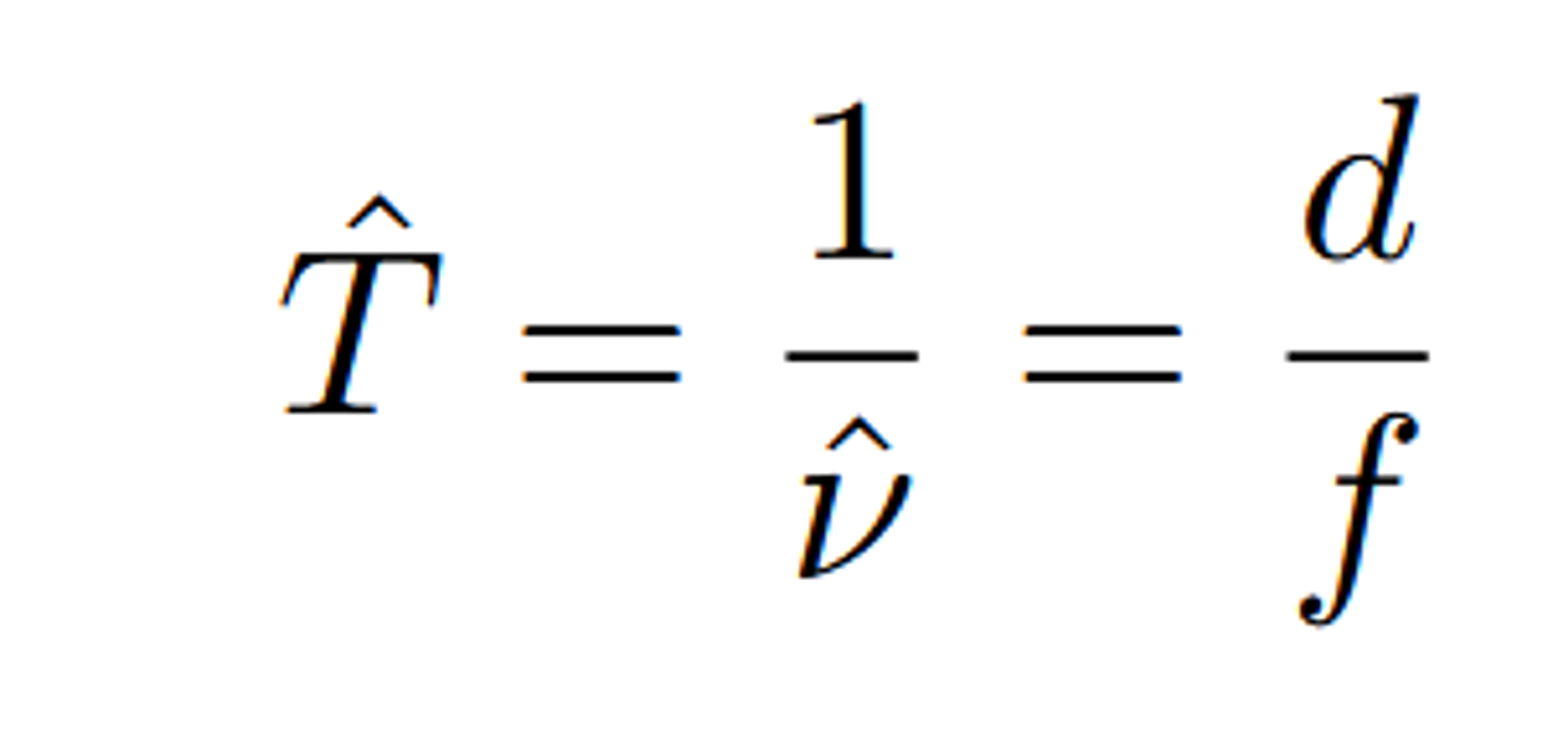
$\hat{T}$는 샘플링 간격으로 샘플링 주파수 $\hat{v}$의 역수 값을 갖습니다.

또한 샘플링 간격은 depth d와, focal lenght f와 d/f의 관계를 갖습니다.

• d: 카메라와 장면 사이의 거리를 나타냅니다.
  • 값이 클수록 더 넓은 시야로 볼 수 있고, 이때는 세부사항이 덜 중요하므로 샘플링 간격을 크게합니다.
  • 반대로 값이 작을수록 장면과 가까이 있으므로 세부사항이 중요해져 샘플링 간격을 작게합니다.
• f: 카메라 렌즈의 초점거리를 나타냅니다.
  • 초점거리가 길어지면 더 좁은 범위를 더 자세히 보기 때문에 샘플링 간격을 작게합니다.
  • 반대로 커지면 더 넓은 범위를 보므로 샘플링 간격을 크게 합니다.

이전에 설명한 Nyquist’s theorem( $\hat{v}$ ≥ 2ν)에 따르면 샘플링 주파수가 최대 주파수 신호의 2배이상 이어야합니다. 다시 설명하면 샘플링 간격은 샘플링 주파수의 역수이므로, 샘플링 간격은 최대 주파수 신호의 절반보다 작아야합니다. 따라서 최대 주파수 신호가 2 $\hat{T}$보다 작으면 aliasing이 발생합니다.

• $n = 1, 2, \ldots, N$:
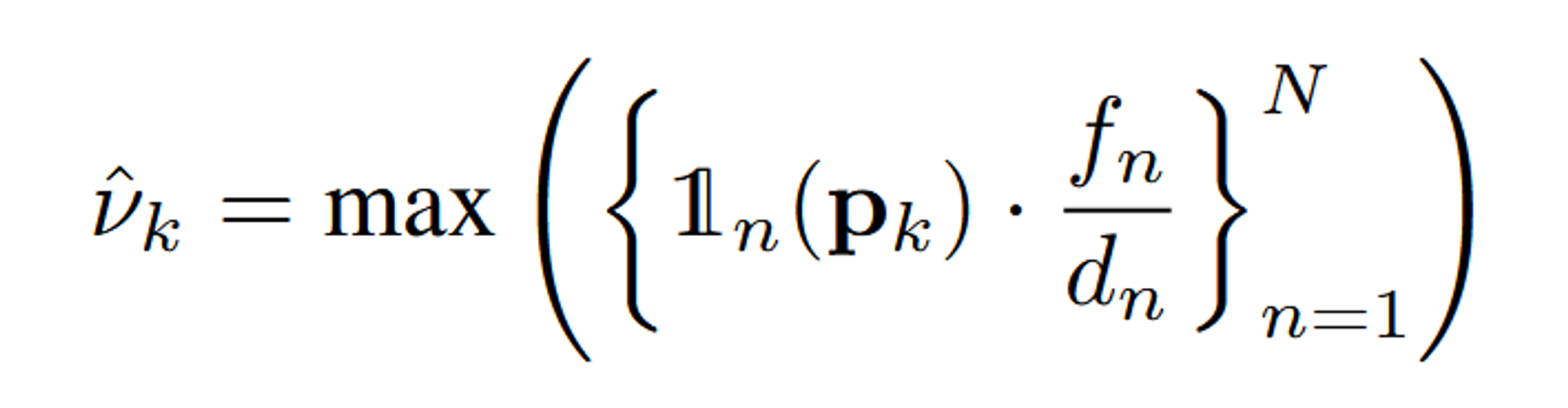
  • 여기서 N은 사용된 카메라 뷰의 수입니다. 각 카메라는 다른 위치에서 장면을 촬영한 것이며, 따라서 각 카메라에 대해 샘플링 주파수를 계산할 수 있습니다.
• $1_n(\mathbf{p}_k)$:
  • 이 함수는 Gaussian primitive $G_k$의 중심 $p_k$가 n번째 카메라의 시야(frustrum) 내에 존재하는지를 나타내는 Indicator 함수입니다. (존재하면 1 아니면 0)
• $\frac{f_n}{d_n}$:
  • $f_n$은 n번째 카메라의 focal length입니다.
  • $d_n$은 n번째 카메라에서 Gaussian primitive Gk의 중심 $p_k$까지의 거리입니다.
  • 이 비율은 해당 카메라에 대해 샘플링 주파수를 나타냅니다.
• $\max \left( \left\{ \cdot \right\} \right)$:
  • 이 부분은 N개의 카메라 중에서 $1_n(\mathbf{p}_k) \cdot \frac{f_n}{d_n}$ 값이 가장 큰, 즉 최대 샘플링 주파수를 선택합니다.

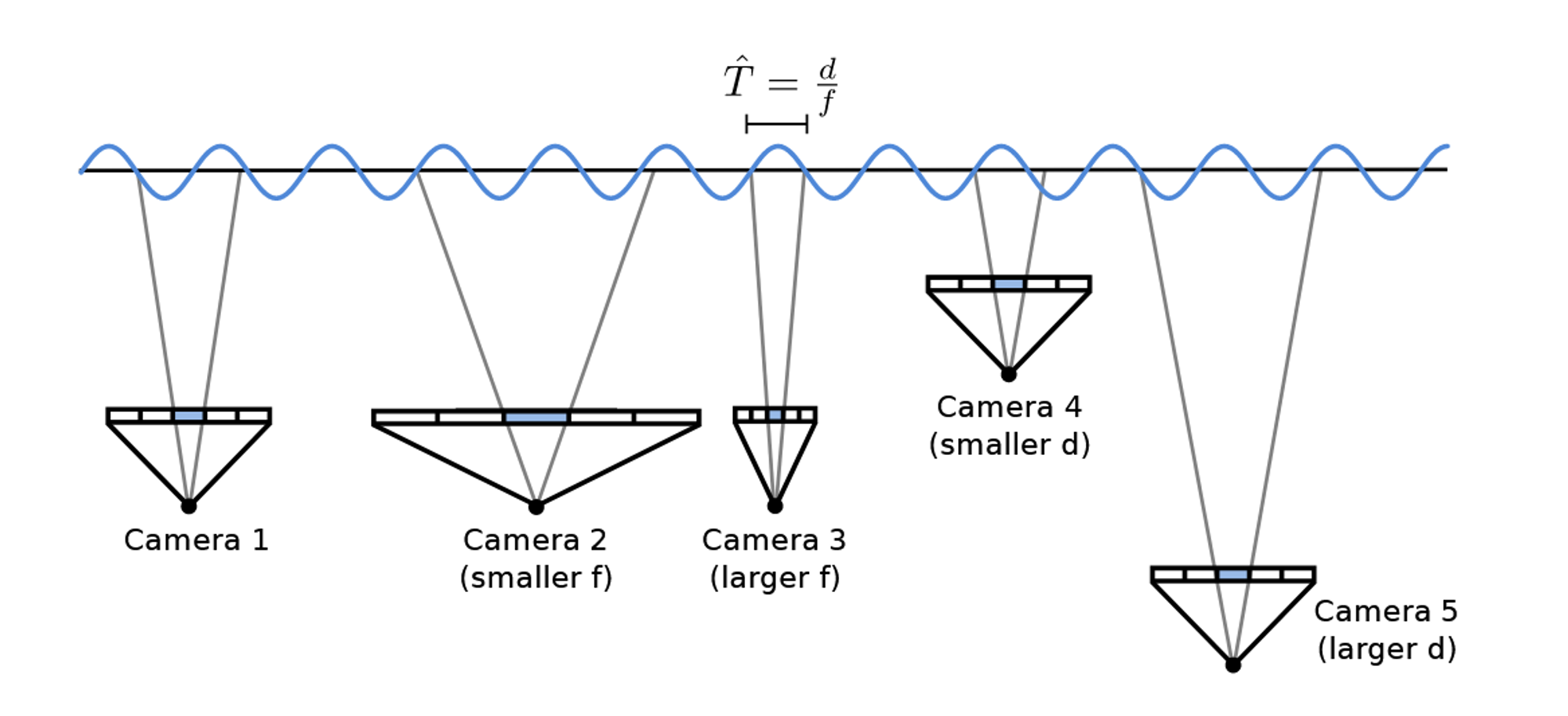
위의 사진은 5개의 Camera에 대해서 f와 d값을 변경했을 때 어떻게 변하는지를 나타내는 것입니다. 최종적으로 Camera3이 선택이 될것으로 보입니다.

Gaussian low-pass filter

위의 과정을 통해서 최대 샘플링 주파수를 고정시키고 Gaussian Low-Pass filter를 적용시켜서 고주파 성분을 제거합니다. 2개의 Gaussian을 합성하는 과정이라고 생각하시면 됩니다.

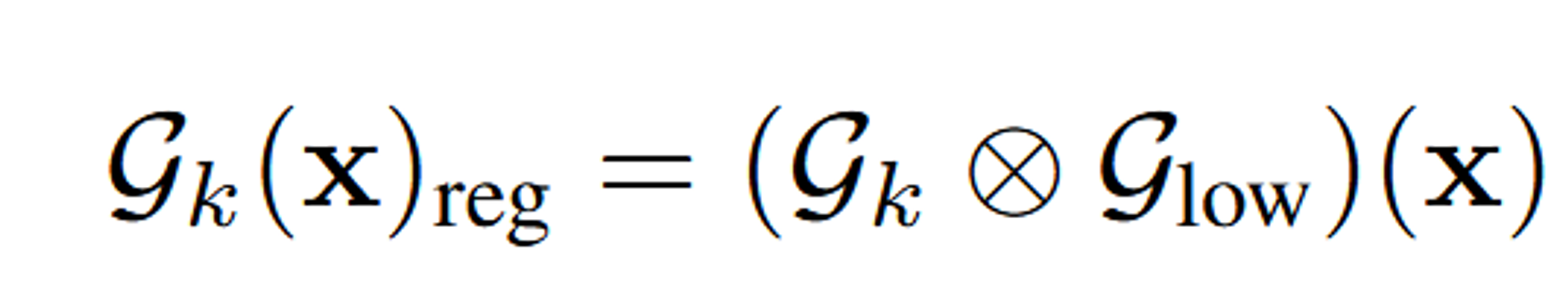
위의 식을 조금더 자세히 적으면 아래와 같습니다.

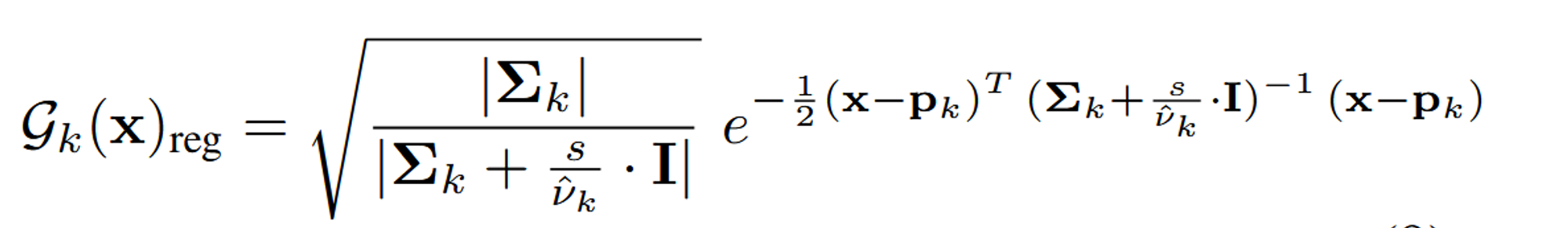
이 식은 Gaussian이 특정 주파수 이상의 정보를 포함하지 않도록 제한하는 효과를 줍니다. 따라서, 이 필터를 적용함으로써 고주파 artifact를 줄이고, 3D 표현의 품질을 향상시킬 수 있습니다.

2D Mip Filter

위에서는 샘플링 주파수를 고정시키고, low-pass filter를 통해서 고주파 성분을 제거했습니다. 다음으로 dilation대신 2D Mip Filter를 통해서 샘플링 속도가 낮아지면서 발생하는 aliasing 문제를 해결했습니다.

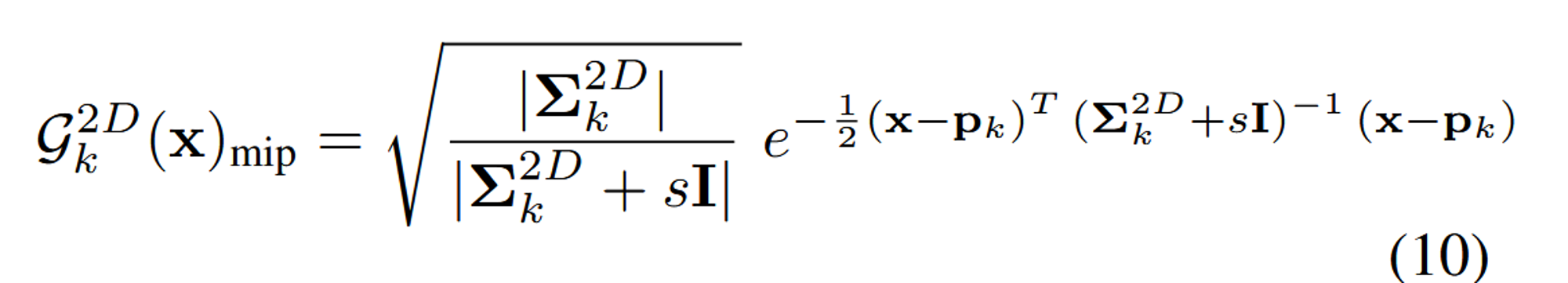
루트안에 있는 부분은 가우시안의 크기를 스케일링 합니다. (s: 하이퍼파라미터 값)

이 필터는 이미지의 디테일을 유지하면서도 에일리어싱을 방지하기 위해 사용되며, zoom in/out이나 샘플링 속도 변경 시에도 적절한 렌더링 결과를 제공합니다.

기존 dilation은 특정 샘플링 비율에서만 효과적이었지만, Box filter를 기반으로한 2D Mip filter는 모든 샘플링 비율에서 효과적으로 작동합니다.

Experiment

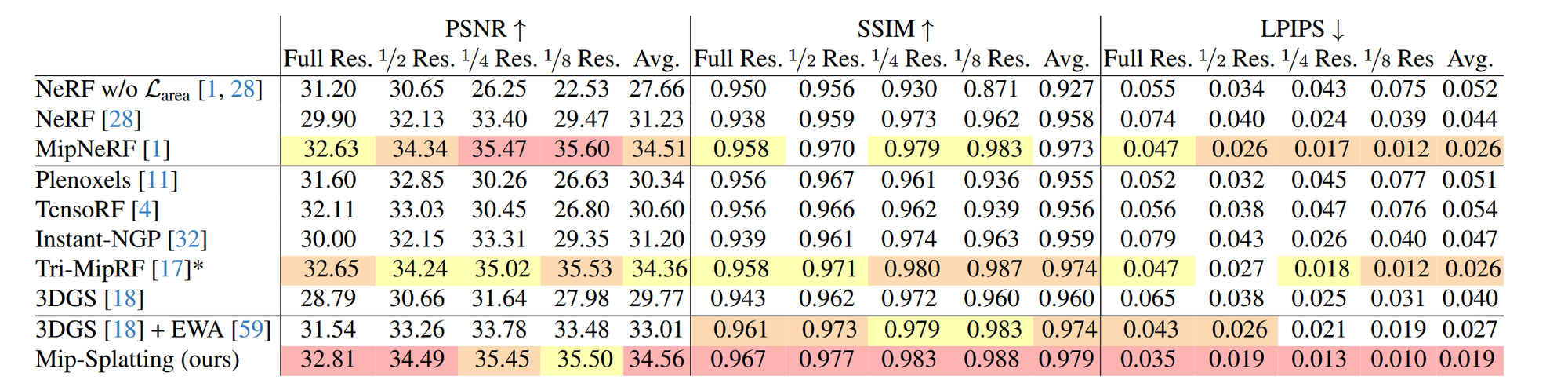
Experiment 부분은 추후에 업데이트 하도록 하겠습니다.

Limitations

• Gaussian 필터의 근사 오차: 박스 필터를 근사하기 위해 Gaussian 필터를 사용하는데, 이로 인해 특히 화면에서 Gaussian이 작아질 때(예: 줌 아웃 상황) 필터링 과정에서 오차가 발생할 수 있습니다. 이 오류는 줌 아웃이 클수록 더 커지는 경향이 있습니다.
• 샘플링 비율 계산의 오버헤드: 매 100번째 반복마다 3D Gaussian의 샘플링 비율을 계산해야 하며, 이 과정이 PyTorch로 구현되어 있어 약간의 트레이닝 오버헤드를 발생시킵니다. 더 효율적인 CUDA 구현으로 오버헤드를 줄일 수 있는 가능성이 제시됩니다.
• 샘플링 비율의 사전 계산과 저장 필요성: 샘플링 비율은 카메라의 위치와 파라미터에 따라 결정되므로, 이를 미리 계산하고 저장하는 더 나은 데이터 구조가 필요할 수 있습니다. 이는 트레이닝 중의 오버헤드를 줄이기 위한 제안입니다.
• 렌더링 중 오버헤드 문제 해결: 제안된 3D smoothing 필터는 트레이닝 후에 Gaussian primitive와 융합되어, 렌더링 시에는 추가적인 오버헤드를 발생시키지 않습니다.