아주 다양한 형태의 3D mesh에 대해 아주 정확하게 다른 공간이나 형태로 변환하는 방법을 deep learning을 이용해서 예측할 수 있는 새로운 프레임워크를 제안합니다.

Approach

기존 Mesh deformation 방법들은 triangulation(삼각형으로 변환한 뒤 진행하는 방법)이 같아야 하는 전제가 있었습니다. 하지만 NJF(Neural Jacobian Fields)는 piecewise-linear-map(조각별 선형 변환)을 예측할 수 있는 프레임워크를 만들어서 어떠한 3D Mesh도 deformation 할 수 있습니다.

입력으로는 Mesh(S)와 global code(z)가 들어옵니다. Global code는 여러가지 값들이 들어갈 수 있는데, 포즈처럼 메시를 어떻게 변형할지에 대한 정보입니다.

Preliminaries

Mesh는 기본적으로 vertex(V)와 face(T)로 이루어져 있습니다. 각 face($t_i$)에 대해 그면에 수직인 벡터 normal이 존재합니다. 이 nomral과 수직인 2차원 평면이 바로 tangent space($T_i$)입니다. 이 tangent space를 좌표로 삼으려면 3차원 공간 속에서 서로 수직이고, 방향이 정해진 벡터인 프레임($B_i$)를 선택해야됩니다.

Piecewise linear maps

각각의 삼각형에서 꼭짓점 3개의 위치를 바꿔가면서 mesh 전체의 구조를 바꾸는 방법을 의미합니다. $V_i → Φ_i$로 새로운 좌표로 이동하는 방식을 사용하는 것입니다. 즉 mesh 전체의 변환(Φ)는 꼭짓점의 새로운 좌표 집합($Φ_i$)만 있으면 완전히 정의됩니다.

Jacobians

Jacobians는 어떤 삼각형 $t_i$에 대해 그 삼각형 평면의 tangent space를 3D 공간으로 가는 linear transformation(3x2)을 말합니다.

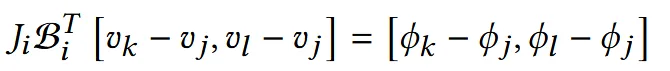
Jacobian을 계산하기 위해서 기존에 설명드린 프레임($B_i$)개념을 사용합니다. 입력과 출력의 3개의 꼭짓점 정보가 주어졌을 때 2개의 변 벡터와 매핑 후 변화를 비교해서 $J_i$라는 3x2 행렬을 계산할 수 있습니다. 이 연산을 프레임 좌표계에서 정의함으로써, 삼각형의 위치, 방향에 상관없이 계산할 수 있게 됩니다. 프레임 좌표계를 사용하면 각각의 삼각형마다 자신의 공간을 정의하는 프레임(basis)가 존재하기 때문에 단순히 Jacobian을 사용해서 2D와 3D의 변환만을 진행하면됩니다. 만약에 프레임 좌표계를 사용하지 않으면 삼각형마다 공간이 다 다르기 때문에 계산이 복잡해집니다.

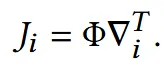
결론적으로 우리는 tangent space에서 3D 공간으로 변환하는 Jacobian행렬을 학습하는 것입니다.

Poisson equation

Jacobian을 정확하게 구했다면 각 삼각형마다 원하는 형태로 변환할 수 있습니다. 하지만 전체 mesh를 어떻게 가장 잘 맞게 만들 수 있을까? 라는 의문이 드실 것입니다.

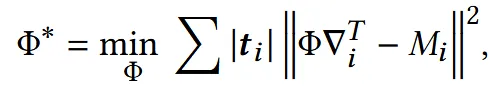
각 삼각형마다 Jacobian($M_i$)가 하나씩 주어져 있을 때 우리가 구하고자 하는 최적의 메시 $Φ^*$는 위의 수식과 같이 각 삼각형의 면적($|t_i|$)와 Φ가 만들 실제 Jacobian($Φ∇_i^T$)와 $M_i$를 최소화하는 방향으로 생성합니다.

실제로 모든 $M_i$를 완벽하게 반영하는 mesh는 구하기 힘들기 때문에 least squares 방식을 사용해서 오차를 최소화하도록 한 것입니다.

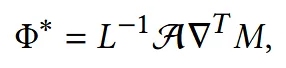
Linear system으로 푼다면 위와 같이 수식을 정리할 수 있습니다.(같은 말이니 이해가 안되시면 생략하셔도 됩니다ㅣ.) A는 삼각형 면적 등으로 만들어진 행렬이고 L은 cotangent Laplacian 그리고 M은 각 삼각형의 jacobian 행렬의 모음입니다. 위 수식을 풀면 $Φ^*$를 한번에 구할 수 있습니다.

Predicting Triangulation-Agnostic, Intrinsic Mappings

해당 프레임워크는 입력 mesh 의 삼각형 개수나 배열에 상관 없이 동작하는 Triangulation-agnostic과 mesh의 실제 디테일을 잘 보존해야하는 Intrinsic, gradient-domain mapping 2가지 목표를 제시했습니다. 이를 위해 2stage 알고리즘을 제시했습니다. 1단계에서는 MLP를 이용해서 임의의 점에 대해 condition으로 global code를 받아서 3x3 행렬을 예측하고, 2단계에서는 3x3 행렬을 tagent space에 맞게 Jacobian으로 변환하고 Poisson solve로 넣어서 실제 메시를 얻습니다. 각 과정을 조금 더 자세히 설명하도록 하겠습니다.

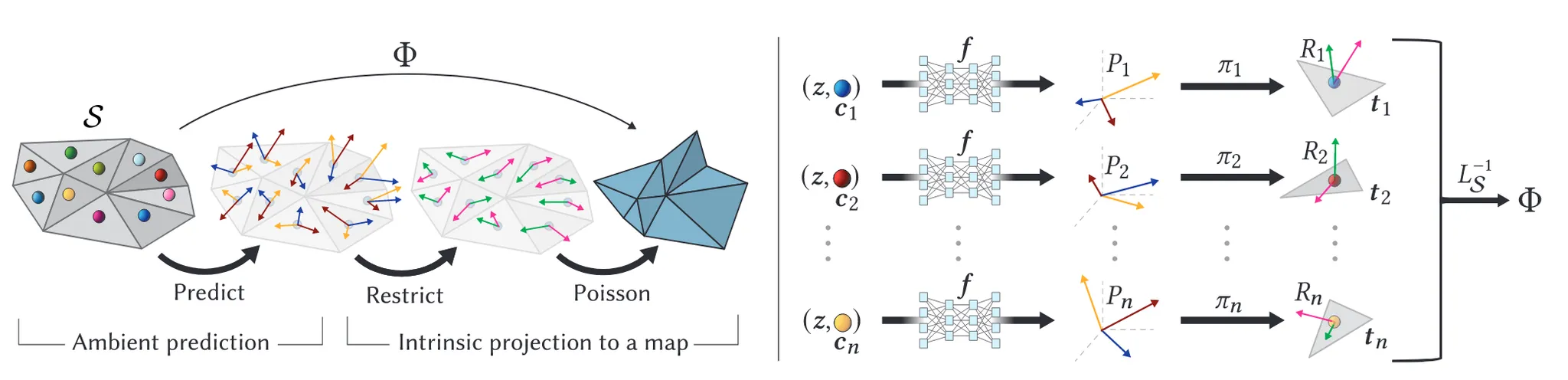
Step1: Predicting matrices in $R^{3X3}$

입력값

• global code(z): Mesh가 어떤 포즈나 상태에 있을지 나타내는 벡터
• point(p): 각삼각형의 중심점($c_i$)사용. 아래 3가지 정보를 합쳐서 입력
  • 3D 위치 좌표
  • Normal vector
  • Wave-Kernel Signature(WKS, 삼각형의 지역적 특징을 요약한 값)

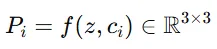
MLP에 병렬적으로 2가지 정보를 넣어서 3x3 행렬 $P_i$를 예측

Step2: Compute a map from the extrinsic field, using the mesh’s intrinsic differential operators

각각의 삼각형 마다 $P_i$를 예측했으니 이걸 각 삼각형의 공간으로 변환하는 jacobian $R_i$를 구해야합니다.

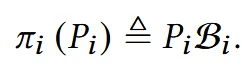
우리는 프레임($B_i$)를 알고 있으니 이를 $P_i$에 곱해서 $R_i$를 위와 같이 얻을 수 있습니다. 최종적으로 jacobian을 Poisson system에 입력하면 우리가 원하는 mesh를 얻을 수 있습니다. Poisson 방정식이 다행히 Linear이기 때문에 backpropagation 이에 대한 역으로 계산만 다시 하면 쉽게 구할 수 있습니다.

빠른 계산을 위해서 각 mesh별로 라플라시안 행렬의 LU 분해를 미리 해두고 이를 이용해서 계산을 진행합니다. 계산전에 진행하는 preprocessing 과정은 위와 같은 알고리즘2처럼 작동합니다.

전처리된 데이터들을 이용해서 Inference하는 과정은 위와 같은 알고리즘1처럼 작동합니다.

Training

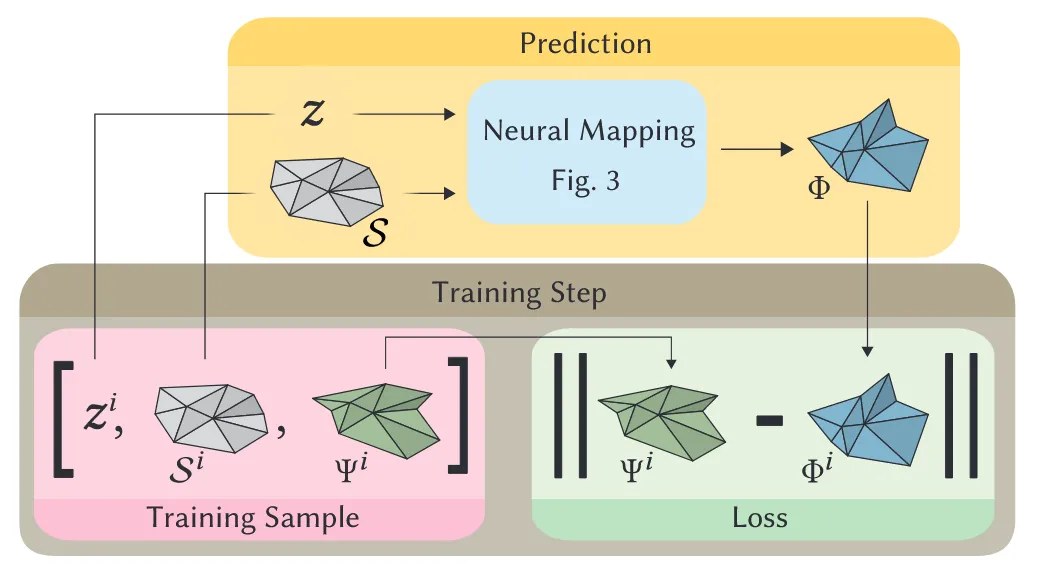
훈련 과정은 위와 같습니다. 사용하는 데이터셋은 변형하고자 하는 mesh인 $S^i$에서 pointNet encoder를 통해서 추출한 global code $Z^i$와 ground truth 값인 $Ψ^i$ 이렇게 3개가 training sample로 들어갑니다. z와 S를 학습시켜서 우리가 예측한 Φ와 Ψ를 비교하면서 2개의 차이를 최소화하면서 학습을 합니다.

Losses

Vertex loss

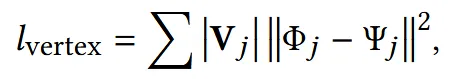
첫번째 loss는 Vertex간 loss로 예측한 Φ와 ground truth Ψ와의 L2 loss입니다. 여기서 $|V_j|$는 해당 꼭짓점 주변의 lumped mass(삼각형 면적)입니다.

Jacobian loss

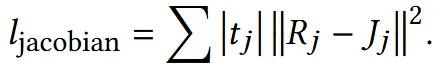
우리가 예측한 Jacobian $R_i$와 ground truth Jacobian $J_i = Ψ∇^T_i$와의 L2 loss를 통해서 차이를 줄입니다. 이전에도 말했지만 $|t_j|$는 j 삼각형의 면적입니다.

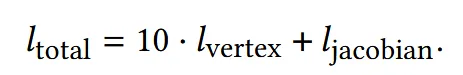
최종적인 loss는 위와 같습니다.

최종적인 학습 방식은 위의 알고리즘 3과 같습니다.

Encoding the global code z and the centroids

Global code z는 크게 2가지로 나눌 수 있습니다. 첫번째로 SMPL pose parameters을 사용하고, 두번째로 Pointnet Encoder로 나온 임베딩 값을 사용합니다.

Discussion: restriction through the frames {Bi}

해당 문단에서는 Frame의 선택에 대해 걱정할 필요가 없는 이유를 설명합니다. Tangent space를 정의하는 basis를 frame이라고 정의했는데, 무작위로 frame을 골라도 문제가 없다고 논문에서 밝히고 있습니다. 왜냐하면 frame이 바뀌면 이에 따라 예측된 jacobian $R_i$도 바뀌고, 동일한만큼 ground-truth jacobian $J_i$도 바뀌기 때문입니다.

RESULTS

Limitation

• Ground truth mapping 데이터셋 필요
• 삼각형별 Jacobian을 계산할 경우 복잡한 곡면 변환은 불가능