Score Jacobian Chaining: Lifting Pretrained 2D Diffusion Models for 3D Generation [CVPR 2023]

이한결·2025년 6월 19일

3D 모델의 기초가 되는 SDS 방식에 대해서 연구를 하는 중 Dreamfusion이 SDS의 시작점이라고 생각했는데, 시작점이 되는 또 다른 논문인 Score Jacobian Chaining을 가져왔습니다. SDS랑 어떤게 다른지, 같다면 정확히 어떤 개념이 사용 됐는지 알아보도록 하겠습니다.

지금까지 아는 SDS 내용을 간략하게 요약하면, Text prompt를 condition으로 사용하는 diffusion 모델을 사용해서 3D를 생성하는 것 입니다.

Preliminaries

Denoising score matching

Score matching loss

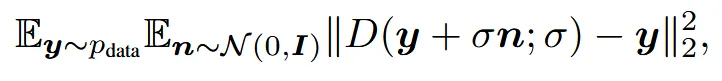
Data(y)에 noise를 더한 형태인 y + $\sigma$ n에서 노이즈를 예측해서 제거하는 denoiser(D)를 통해서 원본 Data(y)를 생성하는 과정이 위와 같습니다. Denoiser(D)는 일반적으로 ConvNet을 사용합니다.

DDPM → Denoiser

Denoiser는 기존 ddpm과 같은 diffusion 모델의 노이즈 예측 모델을 사용하는데, 위의 식처럼 예측한 노이즈를 빼는 형식으로 존재합니다.

Score from denoiser

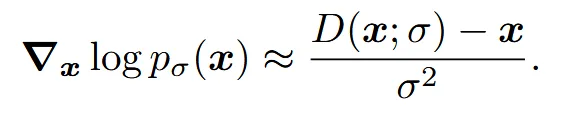
$p_{data}(y)$ 에 표준편차 $\sigma$ 의 gaussain 노이즈를 더한 분포를 $p_{\sigma}(x)$ 라고 정의합니다. 학습된 denoiser(D)는 denoising score(위의 식)을 잘 근사합니다.

결과적으로 위의 수식은 노이즈가 섞인 데이터가 어느 방향으로 가야 원본 데이터로 이동하는지를 학습하는 과정을 나타냅니다.

Score as mean-shift

지금까지 설명한 위의 개념이 mean-shift와 비슷합니다. Denoising score가 원본 데이터로 향하는 방향을 학습한다고 했는데, 이 방향 자체가 mean 방향으로 가는 것과 유사합니다.

Denoiser는 MMSE를 최소화하는 방식으로 학습되는데, MMSE는 posterior의 평균으로 이동하기 때문에 결과적으로 mean-shift와 개념적으로 유사합니다.

Score Jacobian Chaining for 3D Generation

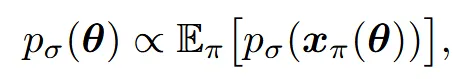
우리에게 2D로 학습된 분포의 정보는 있지만, 3D 분포에 대해서 학습된 정보는 없는 상태입니다. 따라서 우리는 3D 파라미터에 대응하는 voxel의 분포( $p_{\sigma}(\theta)$ )를 여러 시점의 2D 이미지 분포 $p_{\sigma}(x_{\pi}(\theta))$ 의 기댓값에 비례하도록합니다. 여기서 $\pi$ 는 카메라 pose이고, $x_{\pi}(\theta)$ 는 해당 pose에서 렌더링된 이미지입니다. 위의 수식이 이 과정을 나타냈습니다.

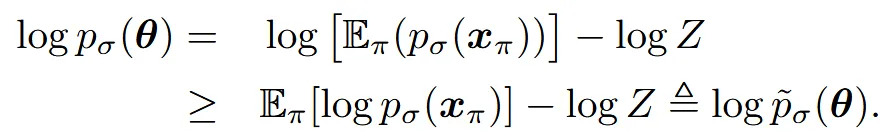
Z는 정규화 상수로서 비례를 부등호로 바꿔주는 역할을 합니다. 이후에 마지막 줄(크거나 같다 부등호 있는 줄)로 바꾸기 위해서 우리는 Jensen’s inequality를 활용합니다. 쉽게 평균을 취한 뒤 log를 씌우는 값이, log를 씌운 뒤 평균을 내는 값 보다 항상 크거나 같다는 것 입니다.

Chain rule에 의해서 3D denoising score는 2D denoising score에 Jacobain render를 곱해주는 결과와 같다는 것을 수학적으로 증명한 것입니다. 간단하게 생각하면, 3D의 score를 학습하기 위해서 결국 2D score를 학습하면 된다고 보시면 됩니다.

Computing 2D Score on Non-Noisy Images

우리는 3D score를 학습 하기 위해서 2D score를 학습해야 되는 점을 알아냈습니다. 그러면 어떻게 2D score를 학습해야 될까요?

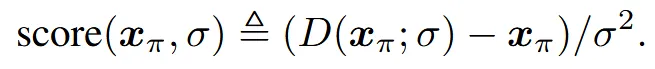
가장 직관적인 방법은 기존의 denoising socre 방식을 그대로 이용하는 것 입니다. 하지만 특정 카메라 시점에서 렌더링 된 이미지는 우리가 전혀 본적 없는 데이터의 분포기 때문에 out-of-distribution(OOD)를 발생시킵니다. 왜냐하면 지금까지 denoising socre는 원본 데이터에 노이즈가 섞인 형태만 봤는데, 렌더링된 이미지는 지금까지 학습한 방식과 전혀 다른 분포이기 때문입니다.

OOD를 위의 예시를 통해서 자세히 설명해 보겠습니다. FFHQ라는 얼굴 데이터로 학습한 이미지에서 주황색 점(blob) 하나만 있는 이미지를 넣으면, 가운데 그림처럼 그냥 artifact가 발생되게 됩니다. 우리가 본 적 없는 데이터의 분포를 갖고 있는 이미지가 입력으로 들어왔기 때문입니다.

Perturb-and-Average Scoring

직관적인 방법을 사용했을 경우 전혀 새로운 분포이기 때문에 잘못된 결과가 나오는 것을 확인했습니다. 따라서 우리는 우리가 학습한 분포로 변환하기 위해 적절한 크기의 노이즈( ${\sigma}n$ )를 더하고, denoiser가 예측한 score를 여러번 샘플링하여 평균을 내면 노이즈 효과가 사라지면서 우리가 원하는 데이터를 얻을 수 있습니다. 이 과정을 Perturb-and-Average Scoring (PAAS)라고 합니다.

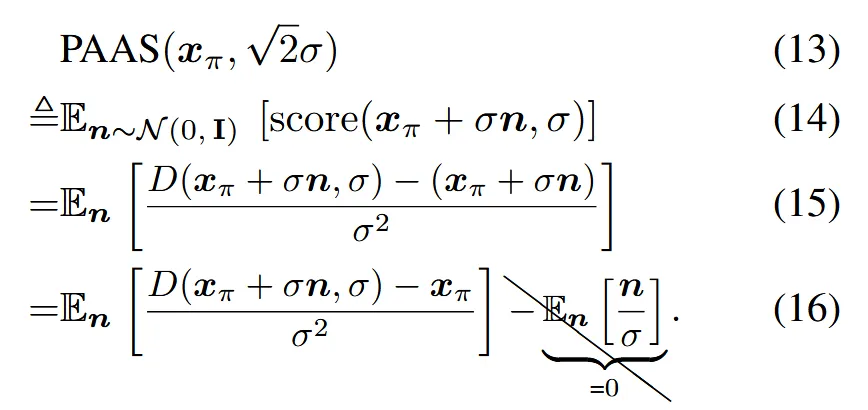
PAAS의 수식 과정은 위와 같습니다.

14 → 15: Denoising score 대입
15 → 16: 노이즈 항 분리(E[n]=0 → i.i.d 정규분포니까!)

실제로는 Monte Carlo estimation 방식을 사용해서 추정합니다.

먼저 렌더링 된 이미지( $x_{\pi}$ ) 주변에서 K개의 노이즈 벡터 ( $n_1 ~ n_K$ )를 샘플링 합니다.(위의 그림 초록색 화살표)
Denoiser를 통해서 파란 점들을 예측 합니다.
파란색 점과, 시작 위치인 초록색 벡터의 끝 점을 이용해서 이동 벡터를 구합니다.

→ 여러개의 파란색 화살표를 평균 낸 결과가 결국 PAAS의 결과랑 유사하다 → Monte Carlo

Justifying PAAS in PAAS(xπ, √2σ)

해당 절에서는 PAAS가 노이즈 세기를 $\sqrt2\sigma$ 로 늘린 분포의 score와 근사한 근거를 2 단계로 제시합니다. 단순히 노이즈 세기를 $\sqrt2\sigma$ 로 정한 이유이기 때문에 수식적으로 확인할 필요가 없으면 건너 뛰어도 괜찮습니다.

한문장 요약: 원본에 표준편차 σ인 Gaussian 노이즈를 한 번 더한 분포(pₛ(x)) 위에, PAAS에서 다시 σ 노이즈를 추가하면 두 독립 노이즈의 분산(σ² + σ²)이 더해져 2σ²가 되고, 따라서 최종 노이즈 세기는 √(2σ²)=√2·σ가 됩니다.

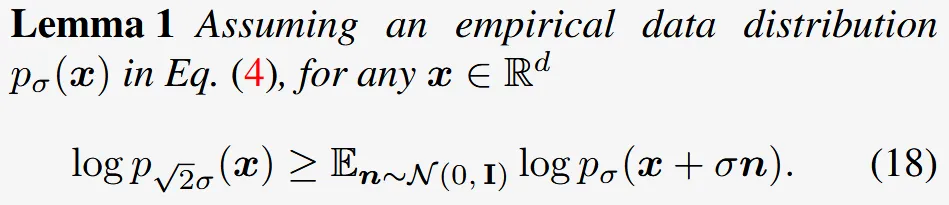
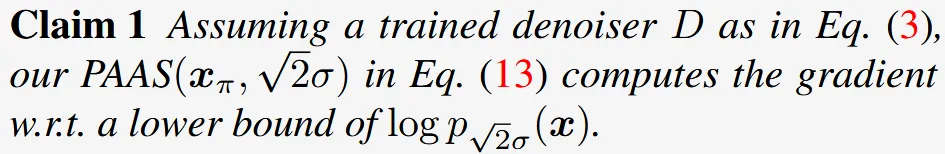
Inverse Rendering on Voxel Radiance Field

3D Representation

3D에서 업데이트 할 파라미터 $\theta$ 를 voxel radiance fiel로 정의 했습니다. $\theta$ 는 density voxel grid( $V^{(density)} ∈ R^{1XN_xXN_yXN_z}$ )와 voxel grid의 생김새 ( $V^{(app)} ∈ R^{cXN_xXN_yXN_z}$ )로 이루어 졌습니다. 일반적으로 appearance는 voxel에서의 RGB 값을 예측하고, c는 3입니다.

Inverse Volumetric Rendering

해당 절에서는 3D voxel을 어떻게 2D로 전환하는지를 나타냅니다.

Camera ray로부터 우리는 동일한 길이(d)로 샘플링을 하고, i번째 Segment 값에서 $(RGB_i, τ_i)$ 를 가져옵니다. 샘플링 된 부분이 정확하게 voxel과 대응하지 않을 수 있기 때문에 보간(trilinear interpolation) 방식을 사용합니다.

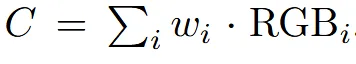
각각의 샘플에서의 weight 값을 이용해서 최종적인 pixel color(C)를 위의 수식으로 예측하게 됩니다.

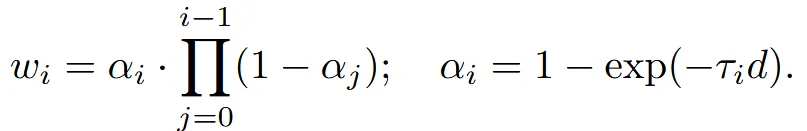
각 샘플의 weight 값은 alpha-composited를 이용해서 위와 같이 구합니다. 간단히 설명하면 픽셀의 불투명도(alpha)에 따라서 가중치가 결정됩니다. τi는 그 지점의 density 값을 나타냅니다.

이 모든 과정은 미분이 가능하고, 따라서 Jacobian을 이용해서 back-propogating이 위의 weight를 구하는 수식이 가능합니다.

Regularization Strategies

Grid 전체에 살짝 denisty를 채워 넣음으로써 그럴싸한 3D를 생성하는 현상을 막기 위해서 정규화 전략을 사용합니다.

Emptiness Loss

작은 밀도로 인해서 작은 $w_i$ 가 생성되는 현상을 막기 위한 정규화 방식입니다. 이를 통해 물체가 존재하지 않는 영역에 흐릿하게 흩어진 점들을 제거할 수 있게 됩니다.

수식적으로 살펴보면 Weight 값에 B(=10)을 곱해줘서, 작은 밀도 값들에 대해서도 penalty를 주게 돼서 흐릿한 점들을 제거할 수 있습니다.

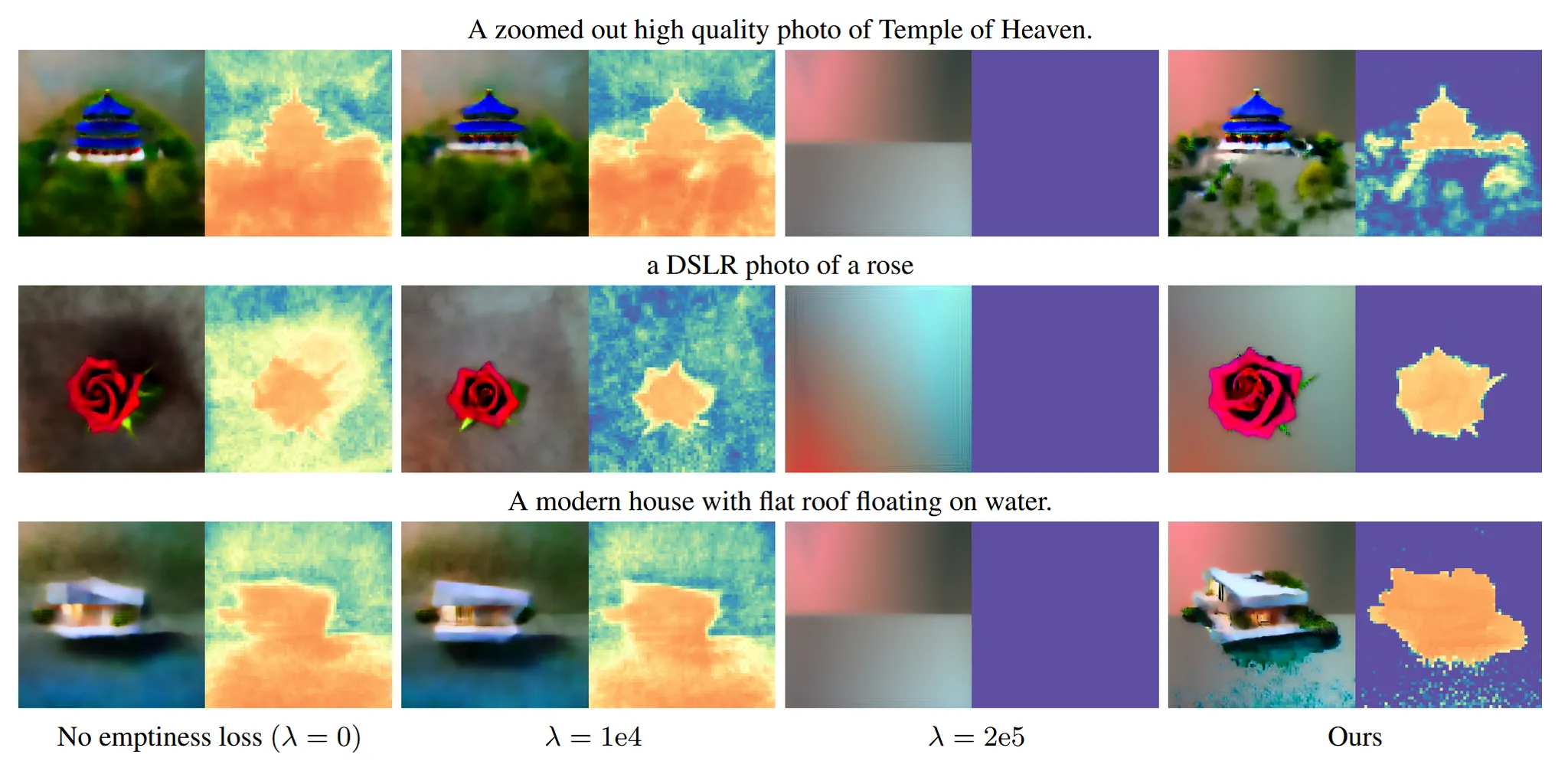
Empatiness loss의 계수(λ)는 초기 K iteration에서 작은 $λ_1 = 1 X 10^4$ 를, 이후 K iteration에서는 조금 더 큰 $λ_2 = 2 X 10^5$ 를 실험적으로 정해서 사용했습니다.

Center Depth Loss

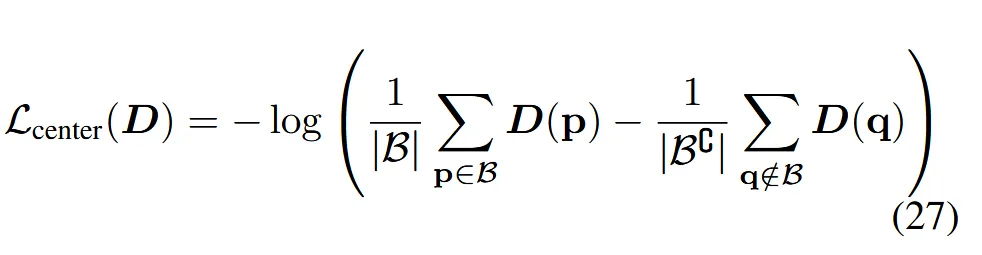
렌더링된 뷰의 중앙과 테두리 픽셀 depth를 비교해, 화면 중심에 물체가 오도록 끌어당기는 손실 함수입니다. D는 depth image, B는 중심 이미지의 box(pixel 위치), $B^C$ 는 B의 complement입니다.

SJC vs. DreamFusion

논문 리뷰 처음에서도 언급한 SDS와 SJC가 어떤 차이가 있는지 자세히 살펴 보도록 하겠습니다.

결론: 같다

Differences from DreamFusion

Dreamfusion에서 U-net jacobian term을 생략하는 것이 더 좋다고 언급했었습니다. SJC에서는 이에 대해서 사용하지 않고 단순히 render jacobian만을 사용했습니다.
OOD의 이유와 노이즈를 추가로 더하는 PAAS 개념을 자세히 설명했습니다.
Dreamfusion은 score residual에서 직접 Monte Carlo방식을, SJC는 denoiser의 출력 자체에 Monte Carlo 방식을 적용. 하지만 성능 면에서 차이는 존재하지 않습니다.

Influences by DreamFusion

Random σ Scheduling: 3D 최적화 단계에서 σ 값을 다양하게 바꿔가며 쓰면 하이퍼파라미터 튜닝이 쉬워진다
View-Augmented Prompting: 카메라 뷰(front view, side view, back view)를 텍스트 프롬프트에 포함시켜주면 3D 품질이 향상된다