SyncTweedies: A General Generative Framework Based on Synchronized Diffusions 논문 리뷰

이한결·2025년 1월 24일

Tweedie’s formula

해당 논문 이름부터 Tweedies라는 개념이 적혀있고, Abstract에서도 Tweedie’s formula를 사용했다고 밝혔기 때문에 해당 개념이 어떤건지부터 자세히 짚고 넘어가도록 하겠습니다.

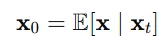
Tweedie 공식은 관찰된 데이터 x에서 클린한 데이터( $X_0$ )를 추정하는 방법 입니다.

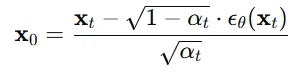
노이즈를 제거? 바로 diffusion 모델을 많은 분들이 쉽게 떠올리실 수 있을 것입니다. 위의 공식이 diffusion 모델의 t시점에서 노이즈를 제거해서 $X_0$ 시점으로 변환해주는 과정입니다. 이 과정이 Tweedie 공식이라고 보시면 됩니다.

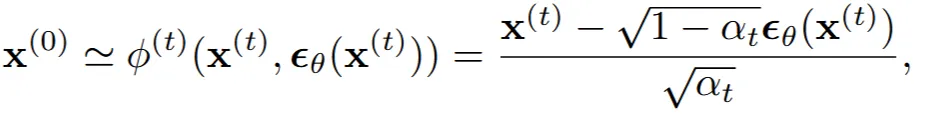
논문에서는 Tweedie 공식을 위와 같이 작성했습니다. DDIM을 설명할 때 작성했으므로 t시점의 정보와 0시점의 정보가 입력값으로 들어가는 것을 알 수 있습니다.

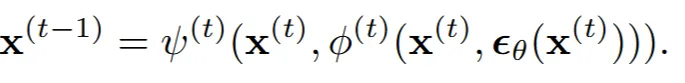
이를 간단한 형태로 나타냈을 때 결론적으로 t-1시점을 예측하기 위해서 t와 0시점을 예측한다. 다시 0시점은 t시점에서 해당 시점의 노이즈를 뺀만큼으로 나타낼 수 있다. 방금 제가 한말을 수식화한 것이 위의 그림이 됩니다.

Problem Definition

NeRF와 같이 여러장의 2D 이미지를 사용해서 3D를 만드는 과정을 기반으로 개념들을 설명해보겠습니다. 일단 최종적으로 생성된 3D 공간을 해당 논문에서는 canonical space $Z$ 라고 정의 했습니다. 그리고 2D 이미지들이 존재하는 공간을 instant space $\{W_i\}_{i=1:N}$ 라고 정의했습니다.

3D에서 2D로의 변환과정은 특정 시점에서 projection을 하면되겠죠? 이렇게 projection 하는 함수를 해당 논문에서는 $f_i: Z → W_i$ 로 표시했습니다. 그리고 그 역변환 2D → 3D의 과정을 unprojection( $g_i$ )라고 정의했습니다.

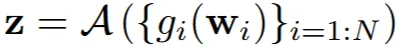
최종적으로 NeRF에서는 여러장의 2D 이미지를 이용해서 3D를 생성하죠? 그 과정을 위와 같이 나타낸 것입니다. 우선 2D → 3D의 과정을 $g_i(w_i)$ 로 나타냈고, 이렇게 변환된 모든 정보를 합치는 과정을 aggregation(A)로 나타낸 것입니다.

Diffusion Synchronization Processes

Instance space(2차원)

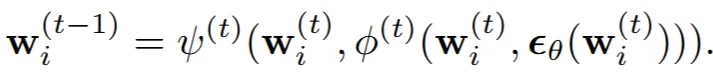
단순히 DDIM의 수식에 x대신 w는 대입한 결과 입니다. w는 2D space 즉 instantce space라고 이전에 설명해드렸죠? 그냥 naive한 방법으로 접근했을 때 instance space상에서 2D 이미지들을 업데이트 하고 이를 기반으로 마지막에 Aggregate(A)해서 3D를 생성할 수 있겠죠? 하지만 이렇게 되면 뷰끼리의 consistency가 일치하지 않아서 좋지 않은 결과를 나타냅니다.

따라서 Instance space에서 계산을 끝까지 한 후 결과를 Aggregation 하는 대신, 계산 과정 중간에 projection & unprojection을 통해 canonical space에서 동기화를 반복적으로 수행함으로서 consistency를 유지시키는 방식을 제시했습니다.

그러면 각 time step 별로 동기화를 할건데 언제 할거냐? 라고 물었을 때 저자는 3가지 경우가 존재한다고 설명했습니다.

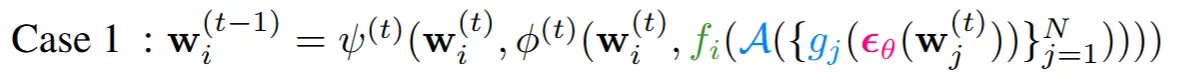
첫번째 경우는 $x_0$ 를 구하는 과정에서 우리는 $x_t$ 에서의 노이즈를 예측하는데, 노이즈를 예측하고 canonical space(3차원)에서 동기화를 진행하고 다시 projeciton으로 동기화된 노이즈를 이용해서 $x_0$ 를 구하는 경우

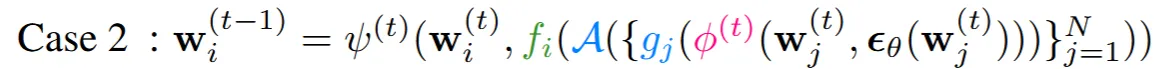
두번째 경우는 $x_0$ 를 예측하고 나서 canonical space(3차원)에서 동기화를 진행하고 다시 projection으로 동기화된 $x_0$ 를 이용해서 $x_{t-1}$ 을 예측하는 경우

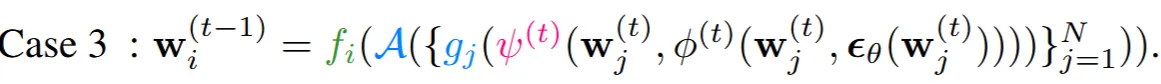
마지막 세번째 경우는 $x_{t-1}$ 까지 예측하고 나서 canonical space(3차원)에서 동기화를 진행하고 다시 projection으로 동기화된 $x_{t-1}$ 을 이용하는 경우

각 경우에서 computation layer(노이즈, $x_0$ , $x_{t-1}$ 예측)를 빨간색으로 표시해뒀습니다.

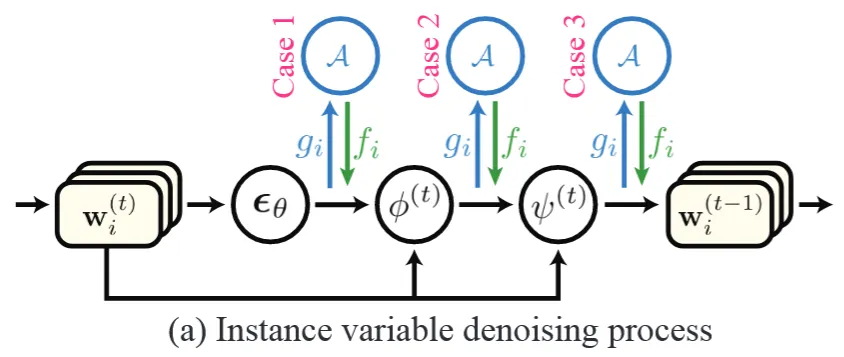
3가지 경우를 시각화 한 것이고 어느 시점에서 동기화를 할지 한눈에 파악할 수 있습니다.

Canonical space(3차원)

이전에는 2차원에서 언제 동기화를 할지 알아 봤었는데, 이번에는 3차원에서 denoising 과정을 진행할 때 언제 동기화할지 알아보도록 하겠습니다. 사실 3차원에서 denoising 과정은 불가능합니다. 3차원 diffusion 모델이 존재하지 않기 때문입니다. 그럼에도 불구하고 아래와 같은 간접적인 방식으로는 가능합니다.

$z^{(t)}$ 상에서 projection을 통해서 canonical space로의 정보를 얻습니다. $f_i(z^{(t)})$
1에서 projection된 각각의 정보들은 denoising 과정을 거칩니다.
2에서 denoising된 정보들을 다시 unprojection( $g_i$ )를 진행하고 Aggregation(A)을 통해서 canonical space상에서의 정보를 얻습니다.

약간 헷갈릴 수 있겠지만 2차원에서는 instance space상의 2D정보를 기준으로 t(time step)를 잡은거고, 지금은 canonoical space상의 3D를 기준으로 t를 잡은거다 라고 생각하시면 이해가 되실겁니다.

어쨌든 이 경우도 2가지 동기화 과정을 진행할 수 있습니다. 해당 과정은 이해를 위해서 전체적인 그림을 먼저 보도록 하겠습니다.

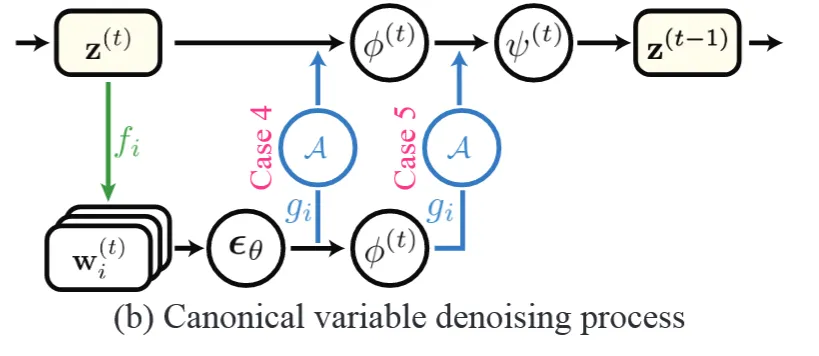
Instance space상에서 노이즈를 예측하고 Aggregate해서 동기화시킬지(Case 4),노이즈 예측하고 $x_0$ 까지 예측하고 동기화 시킬지(Case 5)에 대한 그림인 것을 한눈에 확인할 수 있습니다. 그러면 이제 수식을 확인해보도록 하겠습니다.

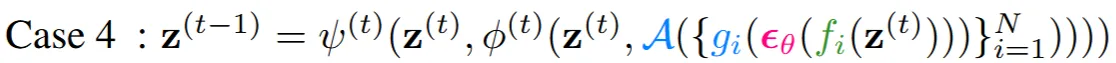
2차원에서는 g→A→f(unprojection → Aggregation → projeciton)이었다면, 3차원에서는 반대로 f→A→g의 형태인 것을 알 수 있습니다. 그리고 이 동기화 과정이 Case4에서는 그림에서 확인했던것처럼 노이즈를 예측한 후 진행됩니다.

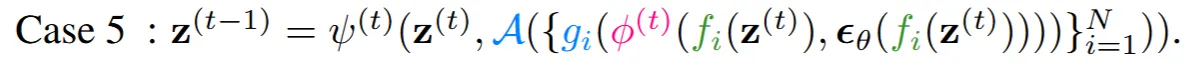
그리고 Case5는 $x_0$ 를 예측하고 진행됩니다.

추가적으로 Instance Space와 Canonical Space에서 동시 노이즈를 예측하는 실험과, Aggregation(A)을 여러번 진행하는 실험도 했지만 성능이 좋지 않았습니다. 이에 대해서 저자가 59개의 케이스로 Appendix H에 작성해주셨습니다.

Connection to Previous Diffusion Synchronization Methods

이부분에서는 이전에 어떻게 동기화를 진행했는지 설명하고 있습니다.

Zero-shot-Based Methods

Ambiguous Image Generation

Ambiguous Image란 시점의 변화(90도 회전, 좌우 반전)로 인해서 다른 이미지가 되는 것을 말합니다. 3차원에서 시점을 변화시킨다음에 2차원으로 projection해서 이미지를 얻을 수 있습니다. Visual Anagrams 논문은 Case 4를 이용해서 Canonical space상에서 noise prediction의 결과를 동기화 했습니다.

Arbitrary-Sized Image Generation

지금까지 Canonical Space가 3차원, Instance Space가 2차원인 경우만 다뤘는데 사실 그렇지 않습니다. 해당 부분에서는 diffusion 모델이 512X512 이미지로 학습되어있는데 임의의 이미지 크기(예:1024X1024)를 생성하기 위해서 512X512를 하나의 패치로 설정하고, 이를 여러개 붙여서 1024X1024사이즈의 이미지를 생성하는 과정을 다룹니다. 여기서 512X512 처럼 하나의 패치를 Instance space, 1024X1024처럼 임의의 이미지 크기를 Canonical space라고 정의합니다. 그러면 projeciton과정은 1024X1024 이미지에서 512X512 이미지를 cropping 하는 과정이 되겠죠? MultiDiffusion과 SyncDiffusion이 $X_{t-1}$ 까지 예측하고 동기화를 진행하는 Case 3를 이용해서 학습을 했었습니다.

Mesh Texturing

Ambiguous Image는 2차원상에서 시점이 변화된 이미지를 다루는 거고, Mesh Texturing은 3D 물체에 어떻게 texture를 입힐지(어떻게 색을 채울지)에 대해서 학습하는 과정입니다. 3D 공간이 canonical space, 렌더링된 이미지가 instance space가 될것입니다(Ambiguous Image에서는 2D공간이 모두 canonical, instance space). SyncMVD 논문이 3차원을 projection해서 $x_0$ 를 예측하고 동기화하는 Case 5를 이용해서 학습을 했었습니다.

Finetuning-Based Methods

이전 연구들중에서 finetuning을 진행해서 동기화를 시도한 것들이 있습니다. SyncDiffusion과 MVDream이 diffusion 모델을 finetuning 해서 다른 시점의 이미지를 생성했습니다. MVDiffusion과 DiffCollage는 360도 파노라마 이미지를 finetuning해서 생성했습니다. 추가적으로 Paint3D 인코더를 학습해서 3D mesh의 texture 이미지를 UV space에서 학습하도록 했습니다. 하지만 이러한 파인튜닝은 적은 수의 데이터로만 진행했다는 단점이 존재합니다. 그래서 오버피팅이 발생하는 경우가 많습니다. 추가적으로 많은 수의 데이터로 학습을 해도 3D texture의 결과는 좋지 않았습니다.

Comparison Across the Diffusion Synchronization Processes

이 부분은 5개의 Case에 대해서 비교해보는 실험을 설명하는 과정입니다.

Toy Experiment Setup: Ambiguous Image Generation

새로운 시점에서의 이미지를 생성하는 Ambiguous Image Genration에 대한 실험 부분입니다. 실험에서는 원본 그대로의 이미지를 잘 생성하는지랑, 약간의 변형(회전, 좌우 반전 등)을 줬을 때 잘 생성하는지 2가지를 확인하려고 합니다.

여기서 3가지로 나눠서 실험을 하는데 canonical space와 instance space의 비율에 따라서 1-to-1, 1-to-n, n-to1으로 나눠지게 됩니다. 1-to-1은 canonical space에서 이미지의 변형을 가한게 하나, 1-to-n은 n개 그리고 n-to-1은 n개의 canonical space가 1개의 instance space로 매핑 되는 것을 말합니다.

1-to-1 Projection

5가지 Case를 비교했을 때 결과가 거의 정량적으로 비슷했습니다.

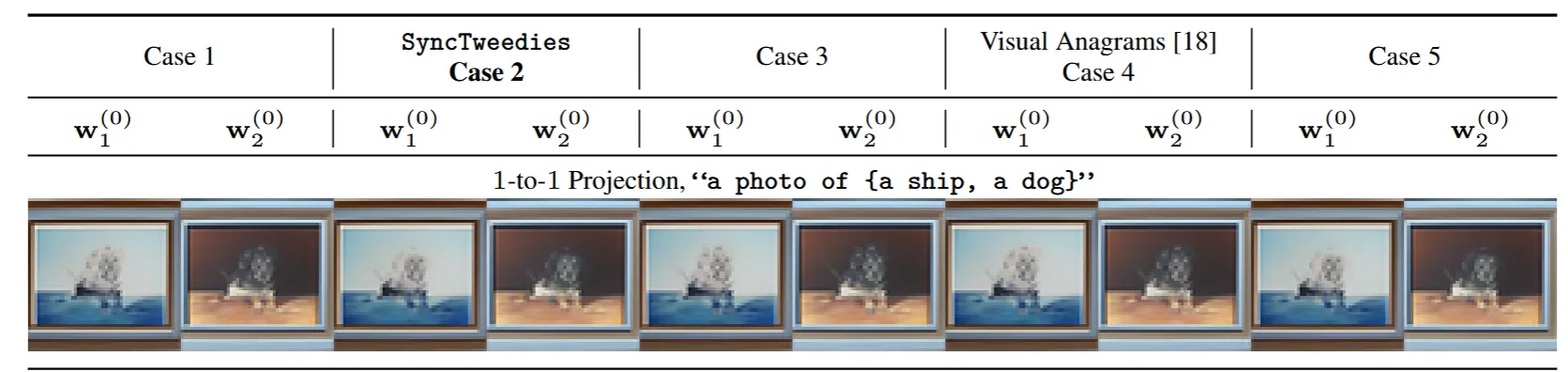
정성적인 비교도 거의 비슷했습니다.

1-to-n Projection

1-to-n Projection의 projection의 역변환이 미분 불가능하다는 문제가 발생할 수 있습니다. 미분이 불가능할 경우 초기 조건인 $f_i(g_i(w_i))=w_i$ 가 성립하지 않게 됩니다.

문제가 발생하는 경우의 예시를 들어드리면, 3D texture를 만들기 위해서 UV Map을 canonical space, 시점에서 projection된 이미지를 instance space라고 가정해보겠습니다. 이때 어떠한 시점에서 하나의 픽셀이 여러개의 instance space에서의 픽셀과 매핑될 수 있습니다. 함수로 조금더 쉽게 설명해드리면 x=1일 때 y=1,2,3의 값을 갖고, x=2일 때 y=2,3,4의 값을 갖는다고 할 때 y=2일 때 역함수가 x=2,3인지 알 수 없다는 점입니다, 단지 reprojection error의 값을 최소화 시키는 방향으로 학습된다는 것입니다.

Case 5개중에서 위의 역변환 문제가 발생하는 경우가 있고, 발생하지 않은 경우가 있어서 1-to-1 projection의 경우보다 성능의 차이가 많이 발생하게 됩니다. Case2,5가 가장 좋은 성능이 나왔고 그다음으로 Case3의 성능이 좋은데 여기서 알 수 있는 점은 denoising 과정이 매우 예민하기 때문에 Tweedie 공식이 적용되기 전에 aggregation을 하면 성능이 안 좋다(Case1,4)는 점입니다.

사진으로 봤을 때도 Case2,3,5가 성능이 좋은 것을 확인할 수 있습니다.

n-to-1 Projection

n-to-1 projection의 대표적인 예시는 NeRF가 될 것입니다. volume rendering을 통해서 여러 3D 상의 픽셀들이 하나의 픽셀로 n-to-1 projection 됩니다. 이경우 역시 1-to-n과 마찬가지로 역변환을 할 때 y에 해당하는 하나의 x값을 명확히 찾을 수 없습니다. 따라서 Case별로 가역 유무에 따라서 성능이 달라지게 됩니다.

추가적으로 1-to-n projection과 다르게 Case 5의 성능이 낮아진 점을 variance decrease 문제가 발생해서라고 설명합니다.

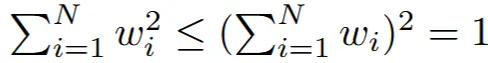
여기서 $w_i$ 는 random variable의 가중치 값입니다. 수학시간에 제곱의 합이, 합의 제곱보다 작다는 수식(triangle inequality(?))에 대해서 들어보신 적 있으실 겁니다. Case5가 첫번째 항에 대한 부분, 그리고 Case2가 가운데 항의 부분으로서 1의 값을 갖습니다. 해당 수식을 통해서 Case5의 가중치 즉 분산이 Case2보다 작은(작거나 같은) 이유가 위의 수식 때문에 발생하고 이 분산이 작은 문제 때문에 성능 차이가 발생한다고 보았습니다. 분산이 감소하면 노이즈가 표현하는 범위가 작아져서 blurry해지거나 단조로워지기 때문입니다.

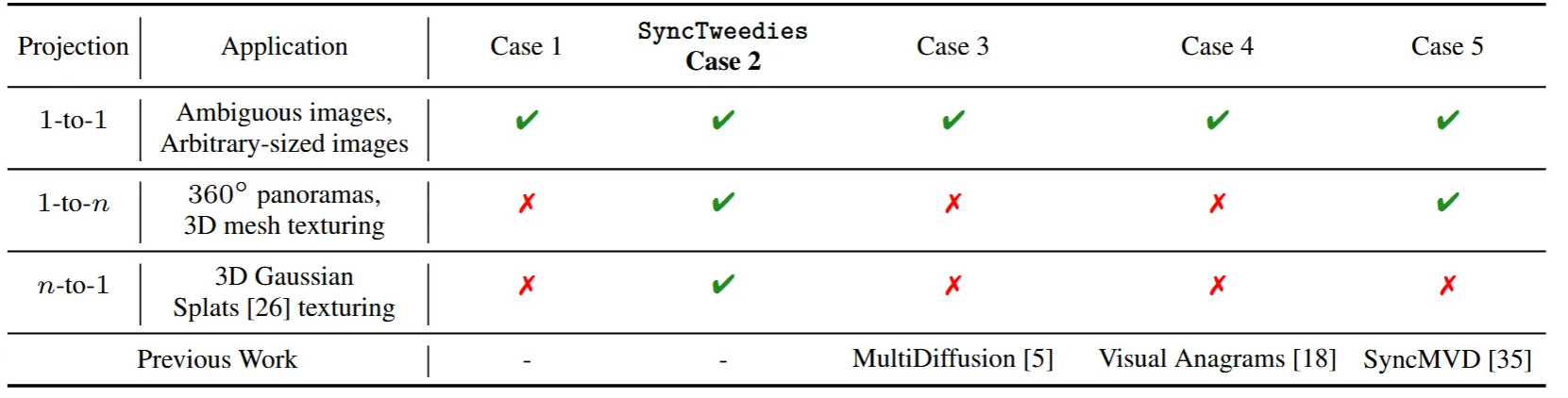
결론적으로 3개의 경우에 따라서 우리는 Case2만이 좋은 성능을 낸다는 것을 확인했고, 해당 경우를 SyncTweedies라고 명명했습니다.

Applications

3D Mesh Texturing

Paint-3D, Paint-it, TEXTure, Text2Tex의 모델과 함께 5개의 Case에 대해서 실험을 진행했습니다. SyncTweedies의 5가지 경우는 SyncMVD와 사전 학습된 diffusion 모델을 기반으로 만들었습니다. 1-to-n projection의 이전결과와 동일하게 Case2,5가 가장 잘나왔고, 나머지 비교 모델 4개보다 잘 나온것을 확인할 수 있습니다.