[머신러닝 완벽 가이드] 5장_회귀 - 다항 회귀

📌 다항 회귀

✅ 개요

• 회귀가 독립변수의 단항식이 아닌 2차, 3차 방정식과 같은 다항식으로 표현되는 것을 다항(Polynomial) 회귀라고 한다.

• 한 가지 주의할 것은 다항 회귀를 비선형 회귀로 혼동하기 쉽지만, 다항 회귀는 선형 회귀라는 점이다.

  • 회귀에서 선형 회귀/비선형 회귀를 나누는 기준은 회귀 계수가 선형/비선형인지에 따른 것이지 독립변수의 선형/비선형 여부와는 무관하다.

예시

다항 회귀식:
$y=w_0+w_1*x_1+w_2*x_2+w_3*x_1*x_2+w_4*x_1^2+w_5*x_2^2$
$=w_0+w_1*z_1+w_2*z_2+w_3*z_3+w_4*z_4+w_5*z_5$

새로운 변수 Z:
$z=[x_1, x_2, x_1*x_2, x_1^2, x_2^2]$

✅ 실습

• 다항 회귀 역시 선형 회귀이기 때문에 비선형 함수를 선형 모델에 적용시키는 방법을 사용해 구현 가능

• PolynomialFeatures

  • degree: 입력 받은 단항식 degree에 해당하는 다항식 피처로 변환

from sklearn.preprocessing import PolynomialFeatures
import numpy as np

# 다항식으로 변환할 단항식 생성, [[0,1],[2,3]]의 2X2 행렬
X = np.arange(4).reshape(2,2)
print('일차 단항식 계수 feature:\n', X)

# degree=2: 2차 다항식으로 변환
poly = PolynomialFeatures(degree=2)
poly.fit(X)
poly_ftr = poly.transform(X)
print('변환된 2차 다항식 계수 feature:\n', poly_ftr) #[[1. 0. 1. 0. 0. 1.]
                                                  # [1. 2. 3. 4. 6. 9.]]

• 단항 계수를 2차 다항 계수로 변환
  $[x_1, x_2]$ → $[1, x_1, x_2, x_1^2, x_1x_2, x_2^2]$

• ex) $[0, 1]$ → $[1, 0, 1, 0, 0, 1]$

• 3차 다항 회귀 함수 예시: $y=1+2x_1+3x_1^2+4x_2^3$

• PolynomialFeatures로 피처를 변환한 후에
  Linear Regression으로 다항 회귀 구현

# 결정 값 반환 함수
def polynomial_func(X):
    y = 1 + 2*X[:,0] + 3*X[:,0]**2 + 4*X[:,1]**3
    return y

X = np.arange(0, 4).reshape(2, 2)
y = polynomial_func(X)

# 3차 다항식 변환 
poly_ftr = PolynomialFeatures(degree=3).fit_transform(X)

# Linear Regression에 3차 다항식 계수 feature와 3차 다항식 결정값으로 학습 후 회귀 계수 확인
model = LinearRegression()
model.fit(poly_ftr, y)
print('Polynomial 회귀 계수\n' , np.round(model.coef_, 2))
print('Polynomial 회귀 Shape :', model.coef_.shape) # (10,)

• Pipeline객체를 이용해 한 번에 다항 회귀를 구현

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
import numpy as np

def polynomial_func(X):
    y = 1 + 2*X[:,0] + 3*X[:,0]**2 + 4*X[:,1]**3 
    return y

# Pipeline 객체로 Streamline하게 Polynomial Feature 변환과 Linear Regression을 연결
model = Pipeline([('poly', PolynomialFeatures(degree=3)),
                  ('linear', LinearRegression())])
X = np.arange(4).reshape(2,2)
y = polynomial_func(X)

model = model.fit(X, y)
print('Polynomial 회귀 계수\n', np.round(model.named_steps['linear'].coef_, 2))

✅ 과소적합 및 과적합

• 다항식의 차수가 높아질수록 매우 복잡한 피처 간의 관계까지 모델링이 가능하다.

• 하지만 다항 회귀의 차수를 높일수록 학습 데이터에만 너무 맞춘 학습이 이뤄져서 정작 테스트 데이터 환경에서는 오히려 예측 정확도가 떨어진다(과적합 발생).

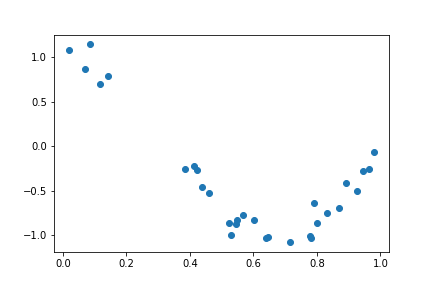
# 다항 회귀를 이용한 과소적합과 과적합 예시

import numpy as np
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score
%matplotlib inline

# random 값으로 구성된 X값에 대해 Cosine 변환값을 반환
def true_fun(X):
    return np.cos(1.5 * np.pi * X)

# X는 0 부터 1까지 30개의 random 값을 순서대로 sampling 한 데이터
np.random.seed(0)
n_samples = 30
X = np.sort(np.random.rand(n_samples))

# y 값은 cosine 기반의 true_fun()에서 약간의 Noise 변동값을 더한 값
y = true_fun(X) + np.random.randn(n_samples) * 0.1

plt.scatter(X, y)

plt.figure(figsize=(14, 5))
degrees = [1, 4, 15]

# 다항 회귀의 차수(degree)를 1, 4, 15로 각각 변화시키면서 비교
for i in range(len(degrees)):
    ax = plt.subplot(1, len(degrees), i + 1)
    plt.setp(ax, xticks=(), yticks=())
   
    # 개별 degree별로 Polynomial 변환
    polynomial_features = PolynomialFeatures(degree=degrees[i], include_bias=False)
    linear_regression = LinearRegression()
    pipeline = Pipeline([("polynomial_features", polynomial_features),
                         ("linear_regression", linear_regression)])
    pipeline.fit(X.reshape(-1, 1), y)
   
    # 교차 검증으로 다항 회귀 평가
    scores = cross_val_score(pipeline, X.reshape(-1,1), y,scoring="neg_mean_squared_error", cv=10)
    coefficients = pipeline.named_steps['linear_regression'].coef_
    print('\nDegree {0} 회귀 계수는 {1} 입니다.'.format(degrees[i], np.round(coefficients),2))
    print('Degree {0} MSE 는 {1:.2f} 입니다.'.format(degrees[i] , -1*np.mean(scores)))
   
    # 0 부터 1까지 테스트 데이터 세트를 100개로 나눠 예측을 수행
    # 테스트 데이터 세트에 회귀 예측을 수행하고 예측 곡선과 실제 곡선을 그려서 비교
    X_test = np.linspace(0, 1, 100)
    # 예측값 곡선
    plt.plot(X_test, pipeline.predict(X_test[:, np.newaxis]), label="Model") 
    # 실제 값 곡선
    plt.plot(X_test, true_fun(X_test), '--', label="True function")
    plt.scatter(X, y, edgecolor='b', s=20, label="Samples")
   
    plt.xlabel("x"); plt.ylabel("y"); plt.xlim((0, 1)); plt.ylim((-2, 2)); plt.legend(loc="best")
    plt.title("Degree {}\nMSE = {:.2e}(+/- {:.2e})".format(degrees[i], -scores.mean(), scores.std()))

plt.show()

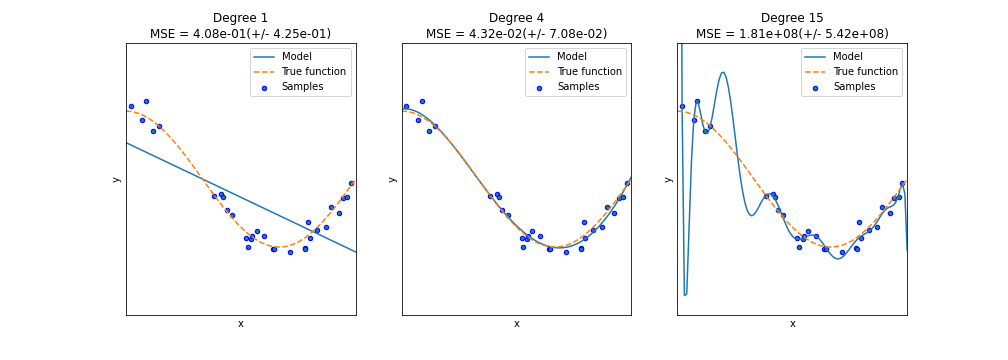
• 실선: 다항 회귀 예측 곡선
• 점선: 실제 코사인 곡선
• 학습 데이터는 0부터 1까지의 30개의 임의의 X 값과 그에 따른 코사인 Y 값에 잡음을 변동 값으로 추가해 구성했으며, MSE 평가는 학습 데이터를 10개의 교차 검증 세트로 나누어 측정해서 평가한 것이다.

• Degree 1: 단순한 직선으로서 단순 선형 회귀와 똑같다. 실제 데이터 세트인 코사인 데이터 세트를 직선으로 예측하기에는 너무 단순해 보인다. 예측 곡선이 학습 데이터의 패턴을 제대로 반영하지 못하고 있는 과소적합 모델로, MSE 값은 약 0.41이다.

• Degree 4: 실제 데이터 세트와 유사한 모습이다. 변동하는 잡음까지 예측하지는 못했지만, 학습 데이터 세트를 비교적 잘 반영해 코사인 곡선 기반으로 테스트 데이터를 잘 예측한 곡선을 가진 모델이다. MSE 값은 약 0.04로 가장 뛰어난 예측 성능을 나타내고 있다.

• Degree 15: MSE 값이 약 180526263가 될 정도로 어처구니없는 오류 값이 발생했다. 예측 곡선을 보면 데이터 세트의 변동 잡음 값까지 지나치게 반영한 결과, 예측 곡선이 학습 데이터 세트만 정확히 예측하고 테스트 값의 실제 곡선과는 완전히 다른 형태의 예측 곡선이 만들어졌다. 결과적으로 학습 데이터에 너무 충실하게 맞춘 과적합이 심한 모델이 되었고 어이없는 수준의 높은 MSE 값이 나왔다.

• 좋은 예측 모델은 Degree 1과 같이 학습 데이터의 패턴을 지나치게 단순화한 과소적합 모델도 아니고 Degree 15와 같이 모든 학습 데이터의 패턴을 하나하나 감안한 지나치게 복잡한 과적합 모델도 아닌, 학습 데이터의 패턴을 잘 반영하면서도 복잡하지 않은 균형 잡힌(Balanced) 모델을 의미한다.

✅ 편향-분산 트레이드 오프 (Bias-Variance Trade off)

• Degree 1: 매우 단순화된 모델로서 지나치게 한 방향성으로 치우친 경향이 있다. → 고편향(High Bias)성

• Degree 15: 학습 데이터 하나하나의 특성을 반영하면서 매우 복잡한 모델이 되었고 지나치게 높은 변동성을 가지게 되었다. → 고분산(High Variance)성

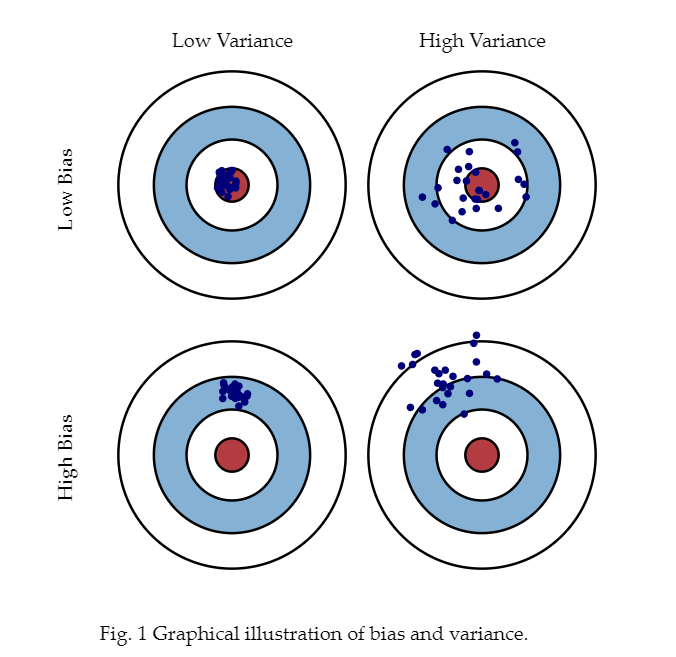
1. 저편향/저분산 (Low Bias/Low Variance)

• 예측 결과가 실제 결과에 매우 잘 근접하면서도 예측 변동이 크지 않고 특정 부분에 집중돼 있는 아주 뛰어난 성능을 보인다.

2. 저편향/고분산 (Low Bias/High Variance)

• 예측 결과가 실제 결과에 비교적 근접하지만, 예측 결과가 실제 결과를 중심으로 꽤 넓은 부분에 분포돼 있다.

3. 고편향/저분산 (High Bias/Low Variance)

• 정확한 결과에서 벗어나면서도 예측이 특정 부분에 집중돼 있다.

4. 고편향/고분산 (High Bias/High Variance)

• 정확한 예측 결과를 벗어나면서도 넓은 부분에 분포돼 있다.

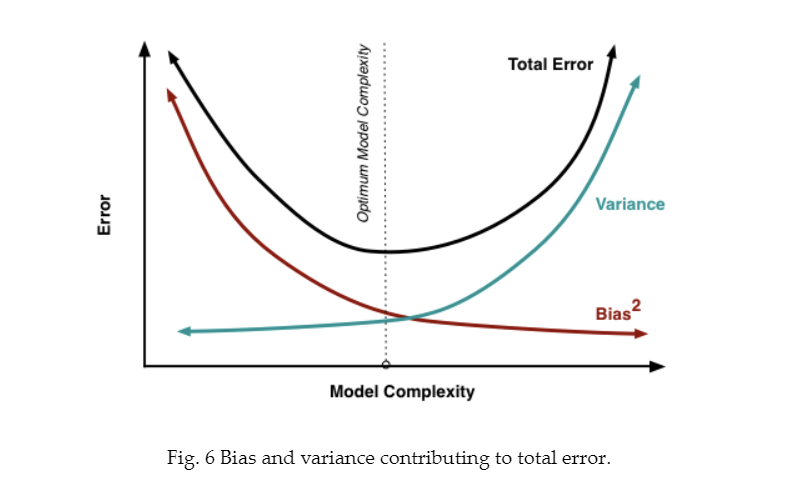
• 높은 편향/낮은 분산에서 과소적합되기 쉬우며 낮은 편향/높은 분산에서 과적합되기 쉽다.

• 편향과 분산이 서로 트레이드오프를 이루면서 오류 Cost 값이 최대로 낮아지는 모델을 구축하는 것이 가장 효율적인 머신러닝 예측 모델을 만드는 방법이다.

이미지 출처