3 Acoustic Feature Extraction
- Mel-Frequency Cepstral Coefficients(MFCC)를 추출하는 방법
- MFCC - 음성 인식과 관련해 불필요한 정보는 버리고 중요한 특질만 남긴 것
- 음성 도메인의 지식과 공식에 기반한 추출 방법
- 음성 입력이 주어지면 피처가 고정된(deterministic) 형태
- MFCC - 음성 인식과 관련해 불필요한 정보는 버리고 중요한 특질만 남긴 것
3-1 Fourier Transform
- 정의: 시간과 주파수 도메인 관련 함수를 이어주는 수학적인 연산
- 음성 신호의 스펙트럼 분석 등에 필수
1] Discrete Fourier Transform
-
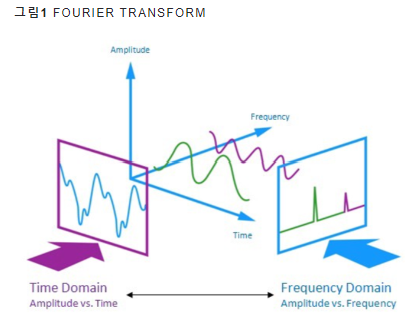
푸리에 변환(Fourier Transform): 시간(time)에 대한 함수(혹은 신호)와 주파수(frequency)에 대한 함수(혹은 신호)를 잇는 수학적인 연산
-
두 개의 단순파(simple wave) -> 시간 도메인에서 복합파로 표현
-
푸리에 변환 실시
-
주파수 도메인에서 두 개의 주파수 성분으로 분해 가능
-
음성 인식 -> 대개 이산 푸리에 변환사용
- 컴퓨터가 이산신호 처리에 적합해서
-
이산푸리에 변환 = 특정 도메인의 이산신호를 다른 도메인의 이산신호로 변환하는 과정
- 이산 = 값이 연속적X, (제외한 시간/주파수에서는 값이 0인 것)
-
이산푸리에 변환
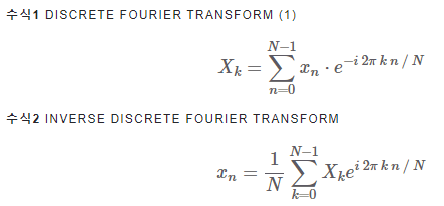
-
역푸리에 변환: 이산 푸리에 변환을 실시한 뒤 이를 다시 원래 도메인으로 변환하는 과정
-
이산 역푸리에 변환: 역푸리에 변환을 이산 신호에 대해서 실시한 것
(exp 지수 부분에 음수 유무 차이)
2] Concepts
-
오일러 공식
- 삼각함수, 지수함수 관의 관계
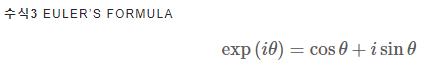
- i는 허수 (제곱시 -1이 됨)
- 오일러의 등식: exp(iπ)+1=0
- exp(iθ) -> 복소 평면상 반지름이 1인 단위원
- 오일러 공식에 의해 실수 + 허수의 합으로 표현 가능
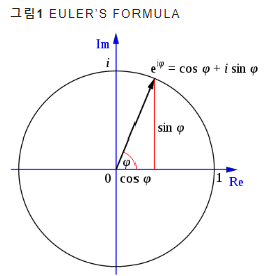
- 오일러 공식에 의해 실수 + 허수의 합으로 표현 가능
- 삼각함수, 지수함수 관의 관계
-
복소 지수 함수 (cis): 오일러 공식에서 바로 유도 가능
- 푸리에 변환의 시작점!
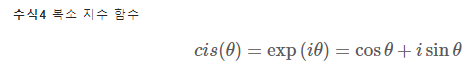
- 푸리에 변환의 시작점!
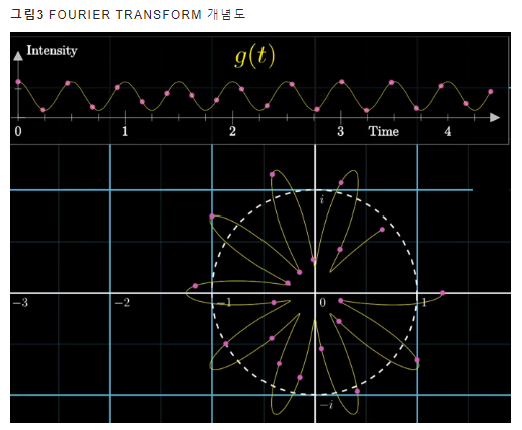
- 시간에서 주파수 도메인으로 푸리에 변환을 실시한다면,
- x_n은 시간 도메인의 n번째 샘플
- x_k는 주파수 도메인의 k번째 푸리에 변환 결과물
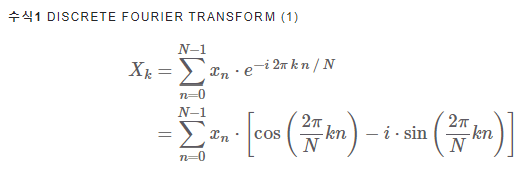
첫쨰줄
- K/N = 복소평면상 단위원에서 얼마나 빠른 속도로 회전하는지 나타내는 각 속도
- n: 시간 인덱스
둘째줄
-
푸리에 변환 결과는 복소수 형태
- 실수부(코사인 함수와 관게 있음) + 허수부 (사인함수와 관계있음)
-
exp 앞에 시간 도메인의 원래 시그널 x_n이 곱해짐
-
지수를 포함한 exp 항: 복소평면 단위원 위에서 이뤄지는 운동
- 단위원의 반지름은 1 -> 수식1의 시그마 안에 있는 점들의 복소평면상 좌표값은 xn
에 의존적일 것
- 단위원의 반지름은 1 -> 수식1의 시그마 안에 있는 점들의 복소평면상 좌표값은 xn
-
복소평면상 이들 점들을 모두 더하는 것 = 이산 푸리에 변환을 적용한 X_k
- 주파수가 k/N 일 때 시간 도메인의 원래 신호의 무게 중심
- X_k => 시간 도메인 원래 신호에서 k/N에 해당하는 주파수 성분
3] DFT Matrix
-
이산 푸리에 변환을 matrix form으로

-
벡터 x: 시간 도메인의 원래 신호
-
행렬 W: 수식1 exp 항에 대응 (N * N), 행 인덱스: k, 열 인덱스:n
- w의 각 행 -> 복소평면상단위원에서 도는 각기 다른 속도
=> 이산푸리에 변환의 본질은, "선형 변환"
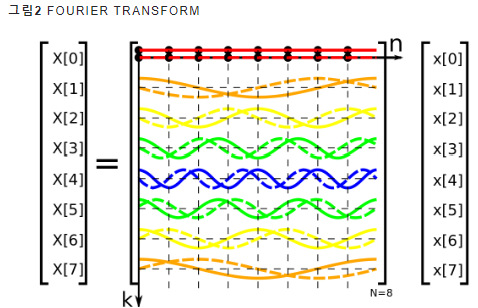
- w의 각 행 -> 복소평면상단위원에서 도는 각기 다른 속도
-
행렬 W = DFT 행렬

4] Python Implementation
- DFT 구현
import numpy as np
def DFT(x):
x = np.asarray(x, dtype=float)
N = x.shape[0]
n = np.arange(N)
k = n.reshape((N, 1))
W = np.exp(-2j * np.pi * k * n / N)
return np.dot(W, x)- Numpy 패키지로 구현
x = np.random.random(1024)
np.allclose(DFT(x), np.fft.fft(x))3-2 MFCCs
음성 인식과 관련해 불필요한 정보는 버리고 중요한 특질만 남긴 피처
Framework
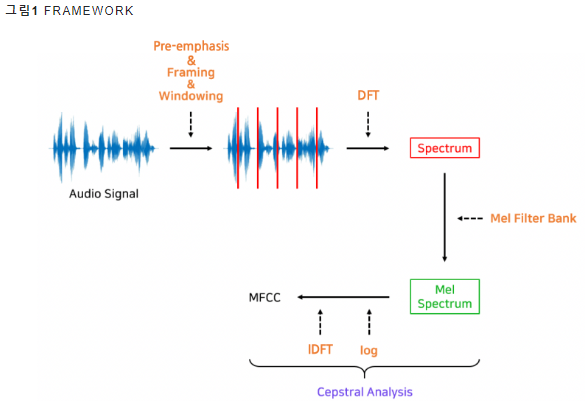
-
입력 음성을 짧은 구간으로 분할
- 잘게 쪼개진 음성 = 프레임
-
프레임 각각에 푸리에 변환 실시 => 해당 구간 음성에 담긴 주파수 정보를 추출
-
스펙트럼: 모든 프레임 각각에 푸리에 변환 실시 결과
-
필터: 스펙트럼에 말소리에 민감한 주파수는 세밀하게, 나머지는 덜 보게 분석하기 위해 쓰임 => 멜 스펙트럼
-
로그 멜 스펙트럼: 멜 스펙트럼에 로그 취함
-
MFCC: 로그 멜 스펙트럼에 역푸리에 변환을 해서, 주파수 도메인의 정보를 새로운 시간 도메인으로 바꾼 것
- 가우시안 믹스처 모델의 입력으로 쓰임 (기존 음성 인식 시스템에서)
-
MFCC: 말 소리 인식에 중요한 특징들 추출한 결과 -> 도메인 지식 활용해 전문가가 공식화한 것 !!
Raw Wave Signal
MFCC 어떻게 만들까???
- wave file 읽기
import scipy.io.wavfile
sample_rate, signal = scipy.io.wavfile.read('example.wav')- dtype=int16 => 음성신호가 16비트로 양자화되어져있다
- 실수 범위의 이산 음성신호가 -32768~32767 범위로 변환 !
- sampling rate가 1초에 몇번 샘플했을까? 이기에 signal 길이를 sample rate로 나누면 음성 시간 확인 가능
len(signal) / sample_rate- 음성 자르기 (앞에서부터 3.5초 자름)
signal = signal[0:int(3.5 * sample_rate)]Preemphasis
-
사람 말소리를 스펙트럼으로 변환해서 관찰하면
- 일반적으로 저주파 에너지가 고주파보다 많음
- => 모음에서 자주 확인
- 고주파 성능 에너지 올리면 => 음성 인식 모델 성능 개선 가능 ! 이걸 하는 전처리를 => preemphasis !
-
다음 세 효과
- 상대적으로 에너지가 적은 고주파를 강화해 원시 음성 신호가 전체 주파수 영역대에서 비교적 고른 에너지 분포를 갖도록 함.
- 푸리에 변환시 발생할 수 있는 numerical problem 예방.
- Signal-to-Noise Ratio(SNR) 개선.
-
t번째 시점의 원시 음성 신호를 xt => 게산 식

-
coefficient α -> 보통 0.95나 0.97을 사용
-
코드
import numpy as np
pre_emphasis = 0.97
emphasized_signal = np.append(signal[0], signal[1:] - pre_emphasis * signal[:-1])Framing
- MFCC 만들 때 푸리에 변환 실시 -> 스냅샷 찍듯이 음성의 주파수별 정보 확인 가능
- 원시 음성 신호는 빠르게 변화하기에, 정확하게 찾기 어려움
- stationary하다 가정할 정도로 -> 아주 짧게 조갬 @@
- stationary = 시점이 변해도 신호가 변하지 X (계속 울리는 사이렌)
- Framing: 음성 신호를 짧은 시간 단위로 쪼개는 과정
- 일정 시간 단위(25ms)로 자르되 일정 구간(10ms)은 겹치도록 => 왜? window 와 관련
frame_size = 0.025
frame_stride = 0.01
frame_length, frame_step = frame_size * sample_rate, frame_stride * sample_rate
signal_length = len(emphasized_signal)
frame_length = int(round(frame_length))
frame_step = int(round(frame_step))
num_frames = int(np.ceil(float(np.abs(signal_length - frame_length)) / frame_step))
pad_signal_length = num_frames * frame_step + frame_length
z = np.zeros((pad_signal_length - signal_length))
pad_signal = np.append(emphasized_signal, z)
indices = np.tile(np.arange(0, frame_length), (num_frames, 1)) + \
np.tile(np.arange(0, num_frames * frame_step, frame_step), (frame_length, 1)).T
frames = pad_signal[indices.astype(np.int32, copy=False)]- pad signal: preemphasis를 수행한 신호(emphasized_signal)에 제로 패딩(z)를 이어붙인 것
- indices: pad_signal에서 인덱스(index) 기준으로 값을 참조하려 만든 변수
- 자세히 보면, 이전 프레임과 다음 프레임이 서로 겹침
- indices와 frames의 shape
- frame size = 25ms, fame_length = 400, sampling rate=16000
- 400이 프레임당 길이
- 348 = num_frames
=> 원시 음성을 짧은 구간(25ms)으로 자르되 일부 구간(10ms)은 겹치게 처리
Windowing
-
정의: 각각의 프레임에 특정 함수를 적용해 경계를 스무딩하는 기법
-
대표 예시: 해밍 윈도우 함수
- => 원리: 개별 프레임에 해밍 윈도우를 적용하면 프레임 중간에 있는 값들은 1이 곱해져 살아남고 양 끝 부분은 0에 가까운 값이 곱해져 그 값이 작아짐
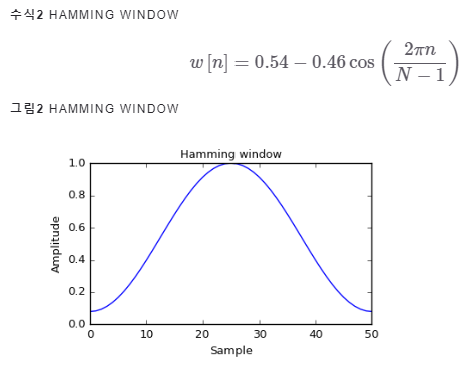
- => 원리: 개별 프레임에 해밍 윈도우를 적용하면 프레임 중간에 있는 값들은 1이 곱해져 살아남고 양 끝 부분은 0에 가까운 값이 곱해져 그 값이 작아짐
-
왜? 이렇게 할까?
- 앞서했던, 원시 음성 신호를 짧은 구간 단위로 잘게 쪼개는 framing은, 그림 3에서 Rectangular Window를 적용한 것이랑 같음
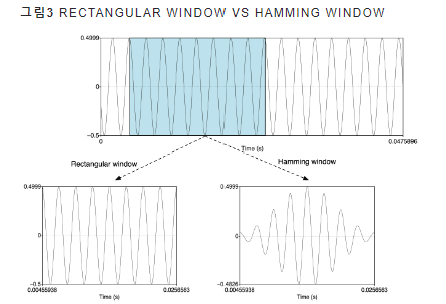
- 앞서했던, 원시 음성 신호를 짧은 구간 단위로 잘게 쪼개는 framing은, 그림 3에서 Rectangular Window를 적용한 것이랑 같음
-
문제점 => Rectangular Window로 자른 프레임의 양끝에서는 신호가 살아 있다가 갑자기 죽는(=0) 상황이 발생 ~> 프레임에 이후 푸리에 변환을 실시하게 되면 불필요한 고주파(high frequency) 성분이 살아남게 됨
-
Hamming window 적용한 경우, 양 끝이 스무딩 되어서 -> 부작용 완화가 가능해짐
Fourer Transform
-
정의: 시간(time) 도메인의 음성 신호를 주파수(frequency) 도메인으로 바꾸는 것
-
이산 푸리에 변환: 이산 신호(discrete signal)에 대한 푸리에 변환
- = 입력 프레임 각 주파수 정보를 확인하는 과정
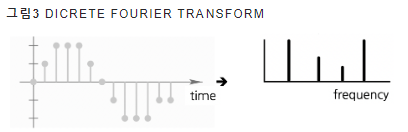
- = 입력 프레임 각 주파수 정보를 확인하는 과정
-
실제 적용할 때 => 고속 푸리에 변환 사용 (기존 방법에서 중복 계산량 줄이는 방법)
-
파이썬 -> np.fft.fft 함수
NFFT = 512
dft_frames = np.fft.rfft(frames, NFFT)- NFFT는 주파수 도메인으로 변환할 때 몇 개의 구간(bin)으로 분석할지 나타내는 인자 (256, 512 주로)
- 근뎅 왜 np.fft.rfft를 썼느냐 -> 과정 생략하게 되어서 결국 똑같다 (계산량 적게 하려면 rfft 쓰자)
Magnitude
- 이산 푸리에 변환의 결과 = 복소수(complex number) = 실수부 + 허수부
- 진폭은 이 주파수 성분의 크기를, 위상은 해당 주파수의 (복소평면상 단위원상)위치
Power Spectrum
- 이산 푸리에 변환 결과(스펙트럼)에 수식3을 적용한 결과를 파워 스펙트럼(Power Spectrum)

- 이산 푸리에 변환 결과가 복소수 형태이어서 -> 모두 실수로 변환
Filter Banks
- 사람의 소리 인식은 1000Hz 이하의 저주파수 영역대가 고주파수 대비 민감함
- 저주파수 영역대세밀하게 보는 과정 필요 => 필터뱅크 사용 (멜 스케일 필터 사용)
Log-Mel Spectrum
- 사람의 소리 인식은 로그(log) 스케일에 가까움
- 두 배 큰 소리라고 인식하려면 -> 에너지 100배 큰 소리 !
MFCCs
- 변수 내 상관관계
- Mel-frequency Cepstral Coefficients(MFCCs): 로그 멜 스펙트럼에 역푸리에 변환(Inverse Fourier Transform)을 수행해 변수 간 상관관계를 해소한 피처
Post Processing
- MFCCs를 입력으로 하는 음성 인식 시스템의 성능을 높이기 위해 몇 가지 후처리
- Lift, Mean Normalization 등