본 논문은 Neurips 2024 에 게재되었다. 작성일자 (24.02.23) 기준 480회나 인용된 논문이다.
1 Introduction
1. 기존 LLM 연구에 대한 의문점
LLM이 많은 사고를 필요로 하는 넓은 범위의 task에서 엄청난 가능성을 보여주고 있다.
이런 방법들은 여전히 text를 생성할 때 autoregressive mechanism가 모든 과정들에 기반해있다. (아직 autoregressiv mechanism 쓰는데도 이렇게 좋은 성능을 내다니 신기해~~)
그런 간단한 방법이 LM이 일반적인 problem solver가 되기에 과연 충분할까? 만일 그렇지 않다면 어떤 것이 현재의 패러다임에 변화를 주면서 대안이 될 수 있을까?
2. Human cognition으로 해결책을 찾아볼까?
human cognition과 관련된 문헌들은 앞선 질문에 답이 될 clue들을 제공한다.
“dual process” model에 관한 연구들은 사람들이 어떤 결정을 할 때 두 가지 모드가 있다고 말한다.
1. 빠르고 자동화된, 무의식적인 모드 (시스템 1)
2. 느리고, 의도적이고 의식적인 모드 (시스템 2)
이 두 모드들은 ML에서 쓰이는 많은 수학적인 모델들과 이전에 연결되어왔다.
예를 들어서, "사람과 동물에 대한 reinforcement learning" 관련 연구는 (1) 그들이 언제 관련있는 "model free" learning에 개입하는지, 아니면 더 (2) 의도적인 "model based" planning에 개입하는지 탐구해왔다.
LM의 간단한 연관 token-level choices는 "System 1"을 연상하며, 의도적으로 "system 2" planning process을 augment하는 것이 더 장점으로 이어질 수 있다 -> 예시로는, (1) 현재 선택에 대해 더 대안적인 것들을 유지/탐색, (2) 현재 상태를 평가하고, 더 global decision을 만들고자 더 앞을 보거나 뒤를 백트래킹하기.
3. 구체적인 방법
그런 계획 방법을 고안하고자, 본 연구에서는 AI의 origin을 반환한다 -> 이 때 선행연구의 planning process에서 영감을 받는다 (Newell, Shaw, Simon)
Newell은 problem solving을 tree로 대변하면서 복합적인 문제 공간을 통한 search로 특징화했다.
그 사실에 기반해서 본 논문은 Tree of Thoughts (ToT) 프레임워크를 언어모델에서의 일반적인 문제 해결 방법으로 제시한다.
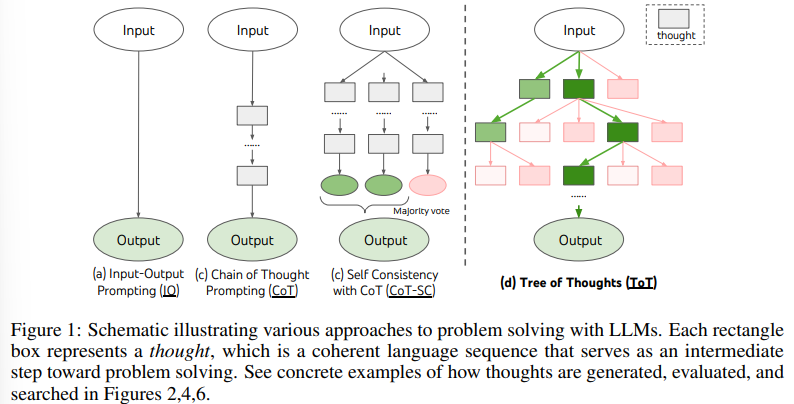
Fig 1에 나와있듯이, 기존 방법들은 문제 해결을 위해 연속적인 언어 시컨스를 샘플링하지만, ToT는 활발하게 tree of thoughts를 진행한다.
ToT에서 각 thought는 문제 해결로 나아가는 데 중간 단계를 역할을 하며, 그는 coherent language sequence다(Table1).
그러한 high-level semantic unit은 LM이 different intermediate thoughts 에 대한 progress를 self-evaluate하도록 하며 문제 해결을 deliberate reasoning process(language에 설명된)로 하도록 유도한다
이처럼 search heuristics을 실행하여 가능해진 LM self-evaluation과 deliberation은 novel하다. 이전 search heuristics이 프로그래밍화되었거나 학습화되었기 때문에.
마지막으로 language-based capability를 결합하였다 -> search algorithms로 다양한 생각들을 생성하고 평가하기 위해서 -> 그런 search algorithms느 BFS, DFS로 ToT가 lookahead, backtracking할 때 systematic exploration을 가능하게 해준다.
경험적 입증을 위한 3가지 문제 상황
경험적으로 본 연구는 기존의 LM inference method를 SOTA 언어모델(GPT-4)로 진행하여 3가지 새로운 문제를 제시했다.
1. Game of 24
2. Creative Writing
3. Crosswords

해당 task 들은 수학적, 기타등등의 능력들을 필요로 하기에 체계적인 계획이나 방법을 통합하는 방법이 필요하다.
본 논문은 ToT가 세 가지 방법 모두에서 우수한 결과를 만들어낸다는 것을 보였였다.
또한 Lm이 한 선택들이 모델 성능에 어떤 영향을 끼쳤는지 알고자 체계적인 ablation study와 future direction을 논의한다.
2 Background
problem-solving을 위해 LLM에서 쓰이는 기존의 방법들을 형식화한다.
pθ: 파라미터 θ로 pre-trained 된 LM을 뜻함
lowercase letters x, y, z, s, · · · : language sequence를 나타냄
x = (x[1], · · · , x[n]) 일 때
x[i]는 token이고,
pθ(x) = Qni=1 pθ(x[i]|x[1...i]).
S : language sequences의 collection
Input-output (IO) prompting
해당 방법은 LM을 사용하여 problem input x를 output y로 바꾸는 가장 흔한 방법이다
y ∼ pθ(y|promptIO(x))
여기서 promptIO(x)는 input x를 task instructions나 few-shot input-output examples로 wrap한다
간단함을 위해,
pθ^prompt(output | input) = pθ(output | prompt(input))라 명명해서,
IO prompting이 y ∼ pθ^IO(y|x)로 공식화될 수 있게 해보자
Chain-of-thought (CoT) prompting
Self-consistency with CoT (CoT-SC)
3 Tree of Thoughts: Deliberate Problem Solving with LM
기존 방법 한계점
인트로 때 언급한 Newell의 연구와 다시 연관지어서 생각해보면,
인간의 문제 해결에 관한 선행 연구는 사람들이 조합적 문제 공간(combinatorial problem space)을 통해 탐색한다는 것을 시사함\
여기서 조합적 문제 공간(combinatorial problem space)란 나무 같은 것으로, 노드는 부분적인 해결책을 나타내고 가지는 그것들을 수정하는 연산자에 해당한다
이렇게 사람이 문제를 해결하는 방법과 관련한 선행 연구에 따르면, 사람은 문제를 해결할 때, 조합적이고 복합적으로 사고해서 결정을 나아간다는 것을 알 수 있다.
하지만 현재까지 문제를 해결할 때 쓰이는 LM의 일반적인 방법들에는 사람이 복합적으로 사고함을 고려할 때 다음 두 가지 단점이 있다.
1) Locally와 관련해서, 기존의 LM은 사고 과정 내에서 다른 계속을 탐색하지 않음 - 즉, 트리의 가지들이 다양하게 뻗어가지 않는다
2) Globally와 관련해서, 기존의 LM은 다양한 옵션을 평가하는 데 도움이 되는 계획, 미래 예측 또는 되돌아가기와 같은 것들을 포함하지 않음
이런 되돌아가기와 같은 휴리스틱 방법들은 인간의 문제 해결에서 특히 특징적이다
Tree of Thoughts (ToT)
앞서 얘기한 두 가지 한계를 극복하고자, 본 연구는 TOT를 제시했다.
ToT는 한 문제에 대해 해결과정을 트리로 만들고 각 노드가 state가 된다고 보고 다음 4가지의 과정을 거치는 패러다임으로 구성된다.
1. intermediate process를 추론 단계 단위로 어떻게 쪼갤 것인가
2. 각 state에서 가능한 thought을 어떻게 생성할 것인가
3. 어떻게 경험적으로 state를 평가할 것인가
4. 어떤 탐색 알고리즘을 쓸 것인가
-
Thought decomposition.
첫번째 단계로, Thought Decomposition을 진행한다.
여기서 Thought는 문제해결에 따라서 문장이 될수도, 단어, 숫자가 될 수도 있다.
24 게임에서는
처음 시작인 4, 9, 10, 13으로 했지만, 10-4를 하는 중간단계를 통해 6, 9, 13이 남게 되는데 이런 식으로 생각을 분해하는 과정을 thought decomposition이라 부름
중간 중간 수식과 남은 숫자들을 표시하여, thought decomposition을 수행하게 됨
그래서 오른쪽 24게임에서는 남은 3개의 중간 결과들이 thought가 되게 된다. -
Thought generator. G(pθ, s, k)
두번쨰 단계는, 현재 상태에서 가능한 다음 생각을 위해 K개의 후보를 생성하는 것이다, 이 때 두 가지 전략을 사용한다
(a) CoT(Chain of Thought) 프롬프트에서 독립적으로 동일하게 분포한(i.i.d.) 생각들을 생성.
이는 thought space가 문단처럼 길어서 풍부할 때 잘 작동하며 i.i.d를 다양화하게 하는 것을 가능하게 해준다.
예를 들어서 task의 목표가 뒤에서 나올 창의적인 글쓰기 이어서, 문단을 쓰는 것 처럼 thought space가 클 때 이 과정이 특히 효과를 발휘한다는 뜻이다.
두번쨰 방법은 아래 그림에 표현되어져있는데,
(b) 제한된 상황에서 다양한 생각을 생성하기 위해 propose prompt를 사용하여 순차적으로 생각하는 것을 제안하는 방법이다.
아래 그림을 활용해서 다시 설명하면,
Possible next step을 통해서 LM이 다음 단계에는 뭐가 남아 있는지 left 10 13 13이런식으로 결과를 알려줌 (그런 노드들이 생기게 됨) -> 그걸 또 넣고 생각을 만들어 내고 이런 과정들이 반복되도록 도와주는 것을 “propose prompt”라 명명함.
- State evaluator V (pθ, S).
3번째 단계에서 나오는 state evaluator는 search algorithm에서 흔히 쓰이는 휴리스틱 처럼 작동하면서 문제를 푸는 과정들을 평가합니다.
여기서 휴리스틱은 탐색하는 과정을 어떤 순서로 할지 결정하는 것을 뜻합니다.
이런 기존의 Heuristics는 탐색문제를 해결하기 위해 딥블루처럼 프로그래밍화되었거나 알파고처럼 학습된 경우가 많은데,
본 논문에서는 이 두가지 방식이 아닌, 또다른 세 번째 방식으로 LM이 state에 대해 의도적으로 reason하는 것을 이용함.
이런 세 번째 방법을 쓰면,deliberate heuristic은 기존에 프로그래밍화해둔 방법보다 더 유연할 수 있고, 학습된 방법보다 더 효율적인 샘플을 할 수 있다는 장점을 가진다.
결론적으로 State evaluator에 해당하는 3번째 단계에서는,
현재 상태를 평가하여 문제 해결에 얼마나 가까운지 판단하는데 크게 두 가지 방법이 있다.
(a) 첫번째 방법은 독립적으로 각 상태를 평가하는 것으로 현재 상태를 숫자 값이나 클래스로 평가하는 것이다.
예를 들어서 1, 2, 3 숫자를 산술기하를 통해 24에 가기에는 너무 모자르다 같은 상황을 평가하는 것이다.
이런 valuation 과정은 완벽할 필요가 없고, 추후에 결정을 내릴 때 도움이 되라고 있는 과정이다.
(b) 두번째 방법은 여러 상태를 비교하는 것으로 주로 vote prompt를 사용하여 상태 간 비교 및 투표하는 과정이 이루어진다.
이렇게 투표하고 비교하는 방법은 self-consistency에서 step-wise를 위해 쓰인 방법과 유사하다.
=> value, vote 두 방법은 모두 BFS, DFS로 LM을 여러번 prompting하면서 작동한다
- Search algorithm.
ToT 프레임워크 내에서는 트리 구조에 따라 다양한 탐색 알고리즘을 연결하고 사용 가능.
우리는 두 가지 비교적 간단한 탐색 알고리즘을 탐구하고 미래 작업에서 더 고급 알고리즘들 (예: A* [11], MCTS [2])을 진행할 예정임
(a) 너비 우선 탐색 (BFS) (알고리즘 1)은 각 단계마다 b개의 가장 유망한 상태를 유지. 이는 Game of 24 및 Creative Writing와 같은 트리 깊이가 제한된 경우 (T ≤ 3)에 사용. 초기 생각 단계를 평가하고 작은 집합으로 가지를 제거 가능 (b ≤ 5).
(b) 깊이 우선 탐색 (DFS) (알고리즘 2)은 가장 유망한 상태부터 먼저 탐색하며, 최종 출력이 도달될 때까지 진행 (t > T) 또는 현재 s로부터 문제를 해결할 수 없다고 상태 평가자가 판단할 때 (V(pθ, {s})(s) ≤ vth, 값 임계값 vth에 대한). 후자의 경우, s에서부터의 하위 트리는 탐사 대 가치 추출을 교환하기 위해 가지를 제거함. 두 경우 모두 DFS는 s의 부모 상태로 백트래킹하여 탐사를 계속함.
개념적으로, ToT는 LMs를 사용한 일반적인 문제 해결 방법으로 여러 가지 이점을 가지고 있음:
(1) 일반성. IO, CoT, CoT-SC 및 자기 수정은 ToT의 특수한 경우로 볼 수 있음 (즉, 제한된 깊이와 너비의 트리; 그림 1).
(2) Modularity. 기본 LM뿐만 아니라 생각 분해, 생성, 평가 및 탐색 절차도 모두 독립적으로 변형 가능.
(3) 적응성. 다양한 문제 특성, LM 능력 및 자원 제약 조건을 수용 가능.
(4) 편리함. 추가적인 교육이 필요하지 않으며, 사전 훈련된 LM만으로 충분함.

4 Experiments
GPT-4 [23]에서 표준 IO 프롬프팅이나 사고 연쇄 (CoT) 프롬프팅을 사용하더라도 어려운 세 가지 과제를 제안.
우리는 의도적인 탐색인 Tree of Thoughts (ToT)에서 더 나은 결과를 얻는 방법과 더 중요한 것은, 탐색이나 계획이 필요한 문제를 해결하기 위해 언어 모델을 사용하는 새롭고 흥미로운 방법을 보여wna. 그 외의 경우를 언급하지 않는 한, 우리는 Chat Completion 모드 GPT-41을 사용하여 실험을 수행하며 샘플링 온도는 0.7임.
4.1 Game of 24
24 게임은 수학적 추론 도전 과제로, 목표는 4개의 숫자와 기본 산술 연산 (+-/)을 사용하여 24를 얻는 것. 예를 들어, 입력 "4 9 10 13"이 주어지면, 해결책 출력은 "(10 - 4) (13 - 9) = 24"가 될 수 있음
Task Setup.
우리는 인간의 해결 시간에 따라 쉬운 것부터 어려운 것까지 정렬된 1,362개의 게임을 가지고 있는 4nums.com에서 데이터를 수집하고, 테스트를 위해 상대적으로 어려운 게임 중에서 인덱스 901-1,000의 하위 집합을 사용. 각 작업에 대해 출력이 입력 숫자를 각각 정확히 한 번 사용하여 24와 같은 유효한 방정식이면 성공으로 간주. 메트릭으로서 100개의 게임 전체의 성공률을 보고.
Baselines.
우리는 5개의 문맥 예제를 사용하는 표준 입력-출력 (IO) 프롬프트를 사용. 사고 연쇄 (CoT) 프롬프팅의 경우, 각 입력-출력 쌍을 3개의 중간 방정식으로 보충하며, 각각은 남은 두 숫자에 대해 작동합니다. 예를 들어, 입력 "4 9 10 13"이 주어지면, 생각은 "13 - 9 = 4 (left: 4 4 10); 10 - 4 = 6 (left: 4 6); 4 * 6 = 24 (left: 24)"가 될 수 있습니다. 각 게임에 대해, 평균 성능을 위해 100번의 IO와 CoT 프롬프팅을 샘플링합니다. 또한 CoT 자기 일관성 기준선을 고려하며, 이는 100개의 CoT 샘플에서 다수의 출력을 취하는 반복적인 개선 접근법을 사용합니다. 각 반복에서 LM은 이전 모든 이력에 대해 조건을 부여하여 "잘못된 답변을 반성하고 개선된 답변을 생성하십시오"라고 명령합니다. 출력이 올바르지 않은 경우. 방정식의 정확성에 대한 실측 피드백 신호를 사용합니다.
ToT Setup.
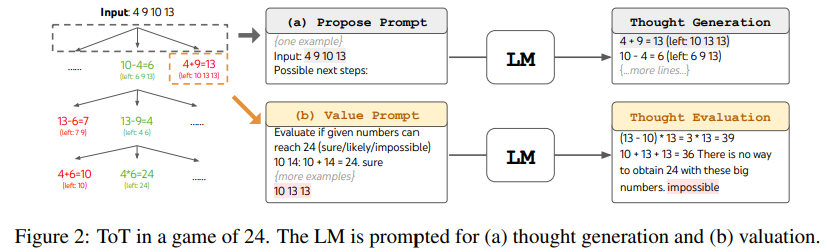
24 게임을 ToT로 구성하기 위해, 생각을 3단계로 분해함, 각각은 중간 방정식입니다. 그림 2(a)에 나와 있는 것처럼, 각 트리 노드에서 우리는 남은 숫자를 추출하고 LM에게 가능한 다음 단계를 제안하도록 합니다. 모든 3개의 생각 단계에 대해 동일한 "제안 프롬프트"를 사용하지만, 이것은 4개의 입력 숫자와 함께한 예제만 있습니다. ToT에서 우리는 너비 우선 탐색 (BFS)을 수행하는데, 각 단계에서 우리는 최고의 b = 5개 후보를 유지합니다. ToT에서 의도적인 BFS를 수행하기 위해, 그림 2(b)에 나와 있는 것처럼, LM에게 각 생각 후보를 "확실함/어쩌면/불가능함"으로 평가하도록 요청합니다. 목표는 몇 가지 미래 예측 시도 내에서 판단 가능한 올바른 부분적 해결책을 촉진하고, "너무 크거나 작은" 상식을 기반으로 불가능한 부분적 해결책을 제거하고 나머지를 "어쩌면"으로 유지하는 것입니다. 각 생각에 대해 값을 3번 샘플링합니다.
Results.
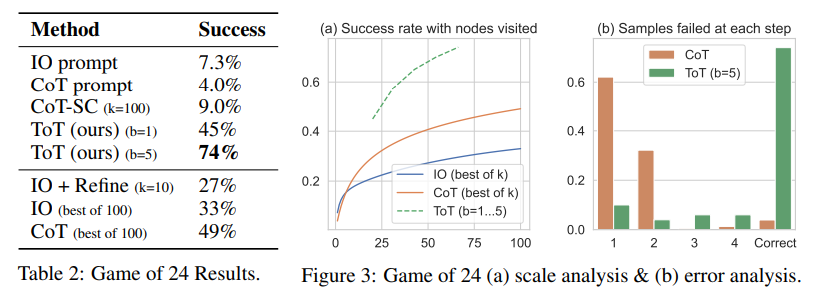
표 2에서 보듯이, IO, CoT 및 CoT-SC 프롬프팅 방법은 작업을 잘 수행하지 못하며, 각각 7.3%, 4.0%, 9.0%의 성공률을 달성합니다. 반면, 너비가 b = 1인 ToT는 이미 45%의 성공률을 달성하고, b = 5인 경우 74%를 달성합니다. 우리는 또한 IO/CoT의 오라클 설정을 고려합니다. 이는 k 개의 샘플 중에서 최고의 성공률을 계산하여 성공률을 계산합니다 (1 ≤ k ≤ 100). IO/CoT (최상의 k)를 ToT와 비교하기 위해, ToT에서 작업 당 방문한 트리 노드 수를 계산하고 b = 1 · · · 5에 걸쳐서 5개의 성공률을 그림 3(a)에 매핑하고, IO/CoT (최상의 k)를 밴딧에서 k 개의 노드를 방문하는 것으로 취급합니다. 예상대로, CoT는 IO보다 더 잘 확장되며, 100 개의 CoT 샘플 중 최상의 k가 49%의 성공률을 달성하지만, 여전히 ToT에서 더 많은 노드를 탐색하는 것보다 훨씬 나쁩니다 (b > 1).
Error analysis.
그림 3(b)는 CoT와 ToT 샘플이 작업을 실패하는 단계를 분석합니다. 즉, 생각 (CoT의 경우) 또는 모든 b 개의 생각 (ToT의 경우)이 잘못되거나 24에 도달할 수 없습니다. 특히, 대략 60%의 CoT 샘플은 첫 번째 단계를 생성한 후에 이미 작업을 실패했습니다. 혹은 동등하게, 처음 세 개의 단어 (예: "4 + 9")입니다. 이것은 직접 왼쪽에서 오른쪽으로 디코딩하는 문제를 강조합니다.
Ref
[1] 유튜브 영상, https://www.youtube.com/watch?v=Yk3jpAhkpUI
[2] 블로그 정리 글, http://blog.mahler83.net/archives/3800