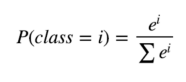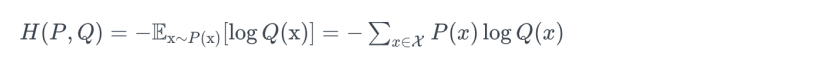Softmax Classification

📒 Softmax Classification

---

이거 먼저 읽기

📝 Softmax

---

• softmax는 하단 수식을 활용해서 모든 확률의 합을 1로 만들어준다.
  

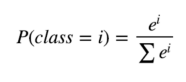
>>> z = torch.FloatTensor([1, 2, 3])
>>> hypothesis = F.softmax(z, dim=0)
>>> print(hypothesis)
tensor([0.0900, 0.2447, 0.6652]) # softmax 적용
>>> print(hypothesis.sum())
tensor(1.) # 합은 1이다.

📝 Cross Entropy

---

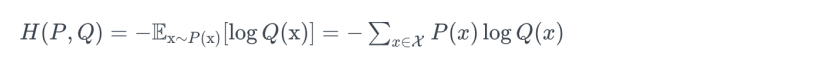
• P, Q 두개의 확률분포가 있다.
• P에서 x를 샘플링하고, Q에 넣은 후에 log를 취한 값의 평균을 구한다.
  
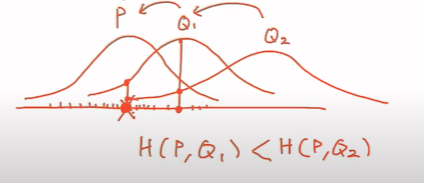
• Q가 점점 P에 가까워지게 만드는 작업이다.
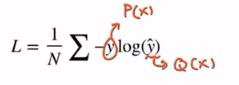
• Loss function은 다음과 같다.
  

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

# 항상 똑같은 결과를 보장하기 위해
torch.manual_seed(1)

z = torch.rand(3, 5, requires_grad=True) # | z | = (3, 5)
hypothesis = F.log_softmax(z, dim=1) # classes = 5, samples = 3
y = torch.randint(5, (3,)).long()
print(y) # 정답 인덱스
# tensor([0, 2, 1])

# 원-핫 벡터로 만들기
y_one_hot = torch.zeros_like(hypothesis)
y_one_hot.scatter_(dim=1, y.unsqueeze(1), 1) # inplace

# cost function 3개가 같은 식
cost = y_one_hot * -F.log_softmax(z, dim=1))).sum(dim=1).mean()
cost = F.nll_loss(F.log_softmax(z, dim=1), y)
cost = F.cross_entropy(z, y)
print(cost)
# tensor(1.4689, grad_fn=<MeanBackward1>)

📝 Training code

---

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

# 항상 똑같은 결과를 보장하기 위해
torch.manual_seed(1)

class SoftmaxClassifierModel(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = nn.Linear(4, 3) # 4개의 Input, 3개의 Output
        
    def forward(self, x):
        return self.linear(x) # | x | = (M, 4) => (M, 3)

# Dataset
x_train = [[1, 2, 1, 1],
           [2, 1, 3, 2],
           [3, 1, 3, 4],
           [4, 1, 5, 5],
           [1, 7, 5, 5],
           [1, 2, 5, 6],
           [1, 6, 6, 6],
           [1, 7, 7, 7]]
y_train = [2, 2, 2, 1, 1, 1, 0, 0] # 정답 인덱스
x_train = torch.FloatTensor(x_train)
y_train = torch.LongTensor(y_train)

model = SoftmaxClassifierModel()
optimizer = optim.SGD(model.parameters(), lr=0.1)

nb_epochs = 1000
for epoch in range(nb_epochs + 1):
    # H(x) 계산
    prediction = model(x_train)
    # Cost 계산
    cost = F.cross_entropy(prediction, y_train)
    # cost로 H(x) 개선
    optimizer.zero_grad()
    cost.backward()
    optimizer.step()
    
    # 100번마다 로그 출력
    if epoch % 100 == 0:
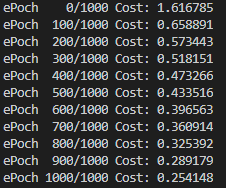
        print('ePoch {:4d}/{} Cost: {:.6f}'.format(epoch, nb_epochs, cost.item()))

• 점점 Cost가 낮아지는 것을 확인할 수 있다.