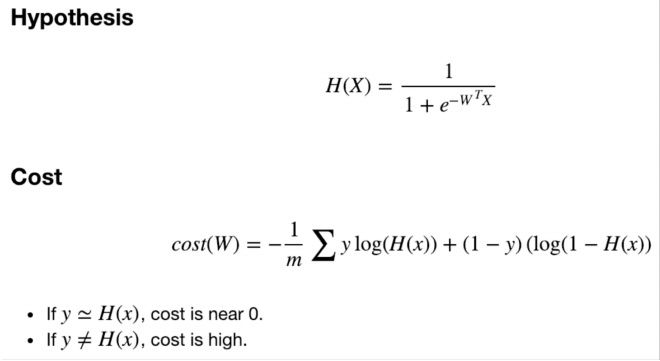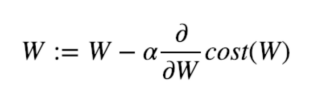Logistic Regression

📒 로지스틱 회귀

---

이거 먼저 읽기

📝 Reminder

---

• M개의 sample로 이루어져있고, D size의 vector의 을 갖는 데이터 X
  👉 M개의 0과 1로 이루어진 정답을 구할 수 있는 model을 구한다.
  
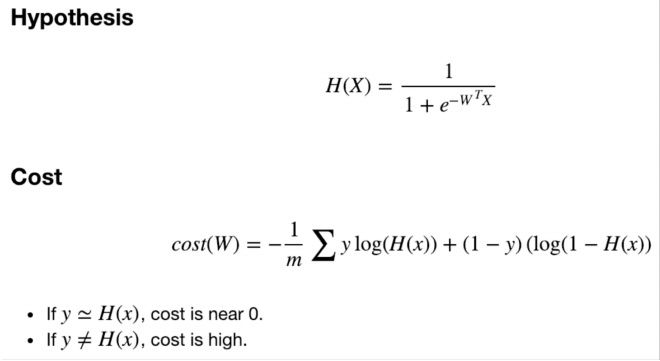
• W는 d개의 값을 갖는 벡터이다.
• Weight를 경사하강법으로 업데이트 하는 수식은 다음과 같다.
  

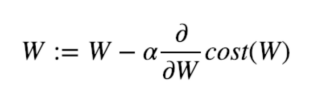
📝 in PyTorch

---

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

# 계속 똑같이 결과를 재현하기 위해서
torch.manual_seed(1)

# Traning Data
x_data = [[1, 2], [2, 3], [3, 1], [4, 3], [5, 3], [6, 2]] # torch.Size([6, 2])
y_data = [[0], [0], [0], [1], [1], [1]] # torch.Size([6, 1])
x_train = torch.FloatTensor(x_data)
y_train = torch.FloatTensor(y_data)

# H(x) 계산
W = torch.zeros((2, 1), requires_grad=True) # 2, 1의 크기를 가져야 됨. (D = 2)
b = torch.zeros(1, requires_grad=True)

# optimizer 설정
optimizer = optim.SGD([W, b], lr=1)

nb_epochs = 1000
for epoch in range(nb_epochs + 1):
    # Cost 계산
    hypothesis = 1 / (1 + torch.exp(-(x_train.matmul(W) + b))) # 수식을 그대로 옮김
    hypothesis = torch.sigmoid(x_train.matmul(W) + b) # 간편한 함수가 구현되어있다.
    losses = -(y_train * torch.log(hypothesis) + \
          (1 - y_train) * torch.log(1 - hypothesis)) # 수식을 그대로 옮김
    cost = losses.mean()
    cost = F.binary_cross_entropy(hypothesis, y_train) # 위 두 줄을 대체하는 간단한 함수이다.
    
    # Cost로 H(x) 개선
    optimizer.zero_grad()
    cost.backward()
    optimizer.step()
    
    # 100번마다 로그 출력
    if epoch % 100 == 0:
        print('Epoch {:4d}/{} Cost: {:.6f}'.format(epoch, nb_epochs, cost.item()))

• 역시 점점 Cost가 감소하는 것을 확인할 수 있다.
  

📝 Higher Implementation with Class

---

class BinaryClassifier(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = nn.Linear(8, 1) # D는 8개
        self.sigmoid = nn.Sigmoid()
        
    def forward(self, x):
        return self.sigmoid(self.linear(x))
    
model = BinaryClassifier()

# optimizer 설정
optimizer = optim.SGD(model.parameters(), lr=1)

nb_epochs = 100
for epoch in range(nb_epochs + 1):
    # H(x) 계산
    hypothesis = model(x_train)
    # cost 계산
    cost = F.binary_cross_entrophy(hypothesis, y_train)
    #cost로 H(x) 개선
    optimizer.zero_grad()
    cost.backward()
    optimizer.step()