📒 페이지랭크
작년 텍스트랭크로 프로젝트를 진행한적이 있어 대충 알고있는 내용이었다.
배경부터 시작해서 밑바닥부터 알아가니까 더 이해가 잘 됐다.
웹페이지로 이런 알고리즘을 만들 생각을 한 구글은 대단하다.
📝 배경
웹은 웹페이지와 하이퍼링크로 구성된 거대한 방향성 있는 그래프이다.
웹페이지는 정점에 해당하고, 웹페이지가 포함하는 하이퍼링크는 해당 웹페이지에서 나가는 간선에 해당한다. 단, 웹페이지는 추가적으로 키워드 정보를 포함하고 있다.
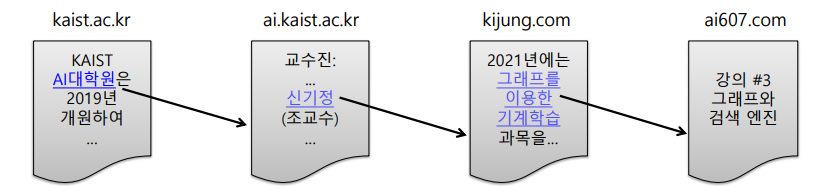
처음에는 웹을 거대한 디렉토리로 정리하였다. 하지만 웹페이지의 수가 증가함에 따라 카테고리의 수와 깊이도 무한정으로 커졌다. 또한, 카테고리 구분이 모호한 경우가 많아 저장과 검색이 어렵다.
다음에는 웹페이지에 포함된 키워드에 의존한 검색 엔진을 시도했다. 이는 사용자가 입력한 키워드에 대해, 해당 키워드를 포함한 웹페이지를 반환한다. 하지만 이 방법은 악의적인 웹페이지에 취약하다는 단점을 갖는다.
📝 정의
페이지랭크의 핵심 아이디어는 투표이다. 즉, 투표를 통해 사용자 키워드와 관련성이 높고 신뢰할 수 있는 웹페이지를 찾는다. 투표의 주체는 바로 웹페이지이다. 웹페이지는 하이퍼링크를 통해 투표를 한다.
사용자 키워드를 포함한 웹페이지를 고려할 때, 웹페이지 u가 v로의 하이퍼링크를 포함한다면 u의 작성자가 판단하기에 v가 관련성이 높고 신뢰할 수 있다는 것을 의미한다. 즉, u가 v에게 투표했다고 생각 할 수 있다.
👉 들어오는 간선이 많을수록 신뢰할 수 있다.
하지만 이는 약용될 소지가 있다. 웹페이지를 여러 개 만들어서 간선의 수를 부풀릴 수 있다. 즉, 관련성과 신뢰도가 높아 보이도록 조작할 수 있다. 이런 악용에 의한 효과를 줄이기 위해 페이지랭크에서는 가중 투표를 한다. 관련성이 높고 신뢰할 수 있는 웹사이트의 투표를 더 중요하게 간주한다. 반면, 그렇지 않은 웹사이트들의 투표는 덜 중요하게 간주한다.
측정하려는 웹페이지의 관련성 및 신뢰도를 패이지랭크 점수라고 부른다. 각 웹페이지는 각각의 나가는 이웃에게 (자신의 페이지랭크 점수 / 나가는 이웃의 수) 만큼의 가중치로 투표를 한다.
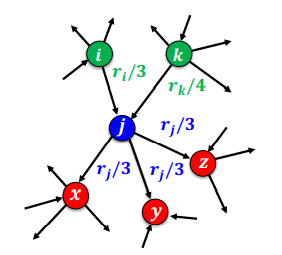
따라서, 페이지랭크 점수의 정의는 다음과 같다.

임의 보행을 통해 웹을 서핑하는 웹서퍼가 t번째 방문한 웹페이지가 i일 확률을 pi(t)라고 하면 p(t)는 길이가 웹페이지 수와 같은 확률분포 벡터가 되어 아래 식이 성립한다.

t가 무한히 커지면, 확률 분포 p(t)는 수렴하여 정상 분포가 된다.
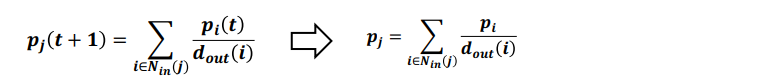
이는, 투표 관점에서 정의한 페이지랭크 점수와 동일하다.
📝 반복곱
페이지랭크 점수의 계산에는 반복곱(Power Iteration)을 사용한다. 이는 세 단계로 구성된다.
- 각 웹페이지 i의 페이지랭크 점수 ri(0)을 동일하게 (1 / 웹페이지의 수)로 초기화한다.
- 아래 식을 이용하여 각 웹페이지의 페이지랭크 점수를 갱신한다.

- 페이지랭크 점수가 수렴하였으면 종료한다. 아닌 경우 2로 돌아간다.
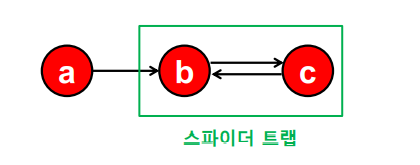
하지만 반복곱이 항상 수렴하는 것을 보장할 수 없다. 들어오는 간선은 있지만 나가는 간선은 없는 정점 집합인 스파이더 트랩(Spider Trap)의 경우가 그렇다.
또 반복곱이 합리적인 점수로 수렴하는 것을 보장할 수 없다. 들어오는 간선은 있지만 나가는 간선은 없는 막다른 정점(Dead End)의 경우가 그렇다.
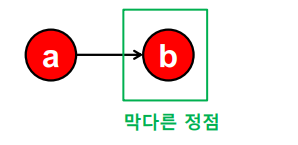
문제 해결을 위해 순간이동(Teleport)을 도입한다. 임의 보행 관점에서, 웹서퍼의 행동을 다음과 같이 수정한다.
- 현재 웹페이지에 하이퍼링크가 없다면, 임의의 웹페이지로 순간이동한다.
- 현재 웹페이지에 하이펄이크가 있다면, 앞면이 나올 확률이 α인 동전을 던진다.
- 앞면이라면, 하이퍼링크 중 하나를 균일한 확률로 선택해 클릭한다.
- 뒷면이라면, 임이의 웹페이지로 순간이동한다.
α를 감폭 비율(Damping Factor)이라고 부르며 값으로 보통 0.8 정도를 사용한다.
이는 페이지랭크 점수 계산을 다음과 같이 바꾼다.
- 각 막다른 정점에서 (자신을 포함) 모든 다른 정점으로 가는 간선을 추가한다.
- 아래 수식을 사용하여 반복곱을 수행한다.
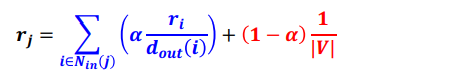
| V | 는 전체 웹페이지의 수를 의미한다.
파란색 부분은 하이퍼링크를 따라 정점 j에 도착할 확률을 의미한다.
빨간색 부분은 순간이동을 통해 정점 j에 도착할 확률을 의미한다.
📒 전파 모형
전파 모형도 이론이 쉽고 간단했다.
networkX를 자주 써보면서 사용법을 익혀놓자.
📝 의사결정 기반 전파 모델
주변 사람들의 의사결정을 고려하여 각자 의사결정을 내리는 경우에 의사결정 기반의 전파 모형을 사용한다. 선형 임계치 모형(Linear Tresholde Model)은 가장 간단한 형태의 의사결정 기반의 전파모형이다.

아래의 상황에서 u가 A를 선택하면 2a가 증가하고, B를 선택하면 3b가 증가한다.
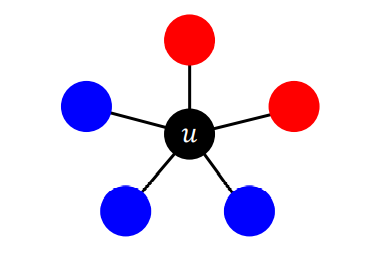
이를 최대화하기 위해서는 2a와 3b중 더 큰 경우를 선택할 것이다. p 비율의 이수이 A를 선택했다고 가정하면, 1 - p 비율의 이웃이 B를 선택했을 것이다. 이때는, ap > b(1 - p)일 때 A를 선택한다.
정리하면, p > b / (a + b) 라는 식이 나온다. 이 식을 임계치 q라고 부른다. 그리고 이 모형을 선형 임계치 모형이라고 한다. 각 정점은 이웃 중 A를 선택한 비율이 임계치 q를 넘을 때만 A를 선택한다.
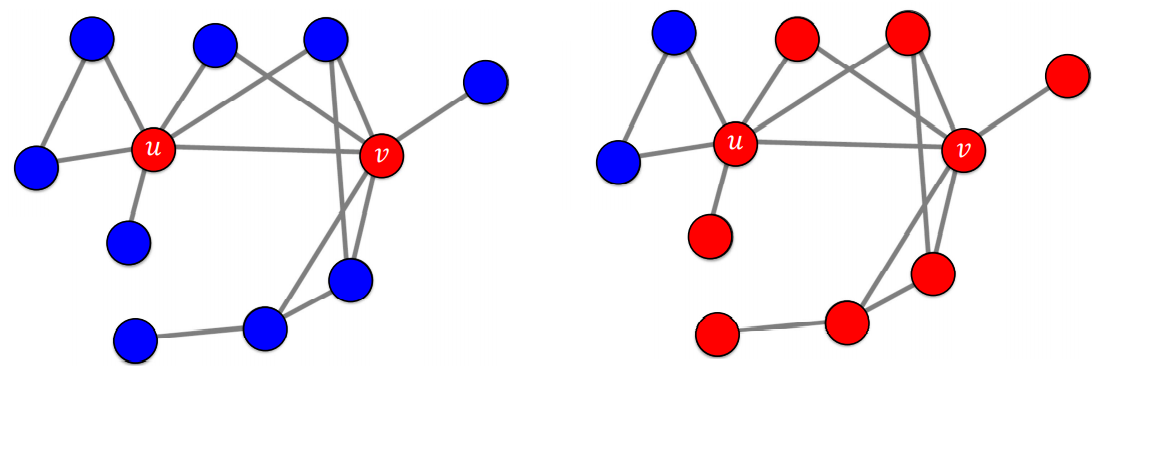
아래 모형은 전부 B를 사용하는 상황을 가정한다. 그리고 처음 A를 사용하는 얼리 어답터들을 가정한다. 시드 집합(Seed Set)이라고 불리는 얼리 어답터들은 항상 A를 고수한다고 가정한다. 왼쪽 얼리어답터 u, v를 포함한 그래프는 전파가 끝나면 오른쪽 모양으로 바뀐다.
📝 확률적 전파 모델
확률적 과정을 갖는 전파는 확률적 전파 모형을 고려해야 한다. 독립 전파 모형(Independent Cascade Model)은 가장 간단한 형태의 확률적 전파 모형이다.
아래 방향성이 있고 가중치가 있는 그래프에서 각 간선 (u, v)의 가중치 puv는 u가 감염되었을 때(그리고 v가 감염되지 않았을 때) u가 v를 감염시킬 확률에 해당한다. 즉, 각 정점 u가 감염될 때마다, 각 이웃 v는 puv 확률로 전염된다.
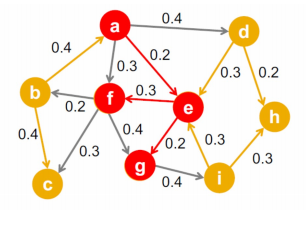
모형은 최초 감염자들로부터 시작한다. 첫 감염자들을 시드 집합(Seed Set)이라고 부른다. 각 최초 감염자 u는, 각 이웃 v에가 puv 확률로 병을 전파하며 이를 새로운 감염자가 없을때까지 반복한다.
📝 전파 최대화
바이럴 마케팅은 소비자들로 하여금 상품에 대한 긍정적인 입소문을 내게 하는 기법이다. 이를 효과적으로 하기 위해서는 소문의 시작점이 중요하다. 시작점이 어디인지에 따라서 입소문이 전파되는 범위가 영향을 받기 때문이다. 따라서 시드 집합은 전파 문제에서 중요한 역할을 갖는다. 그래프, 전파 모형, 그리고 시드 집합의 크기가 주어졌을 때 전파를 최대화하는 시드 집합을 찾는 문제를 전파 최대화(Influence Maximization) 문제라고 부른다. 하지만 최고의 시드 집합을 찾는 것은 NP-hard이다.
전파 최대화 문제의 대표적 휴리스틱으로 정점의 중심성(Node Centrality)을 사용한다. 이는 시드 집합의 크기가 k개로 고정되어 있을 때, 정점의 중심성이 높은 순으로 k개의 정점을 선택하는 방법이다. 정점의 중심성으로는 페이지랭크 점수, 연결 중심성, 근접 중심성, 매개 중심성 등이 있다. 합리적인 방법이지만 최고의 시드 집합을 찾는다는 보장은 없다.
그리디 알고리즘 역시 많이 사용된다. 이는 아래의 순서를 갖는다.
- 정점의 집합 {1, 2, ... , | V |} 을 비교하여 전파를 최대화하는 시드 집합을 찾는다. 이 때, 전파의 크기를 비교하기 위해 시뮬레이션을 반복하여 평균 값을 사용한다. 뽑힌 집합을 { x }라고 한다.
- 집합 {x, 1}, {x, 2}, .. , {x, | V | }를 비교하여, 전파를 최대화하는 시드 집합을 찾는다. 뽑힌 집합을 {x, y}라고 한다.
3 위 과정을 목표하는 크기의 시드 집합에 도달할 때까지 반복한다.
이는 최초 전파자 간의 조합의 효과를 고려하지 않고 근시안적으로 최초 전파자를 선택하는 과정을 반복한다. 독립 전파 모형의 경우 이론적으로 정확도가 일부 보장된다.

