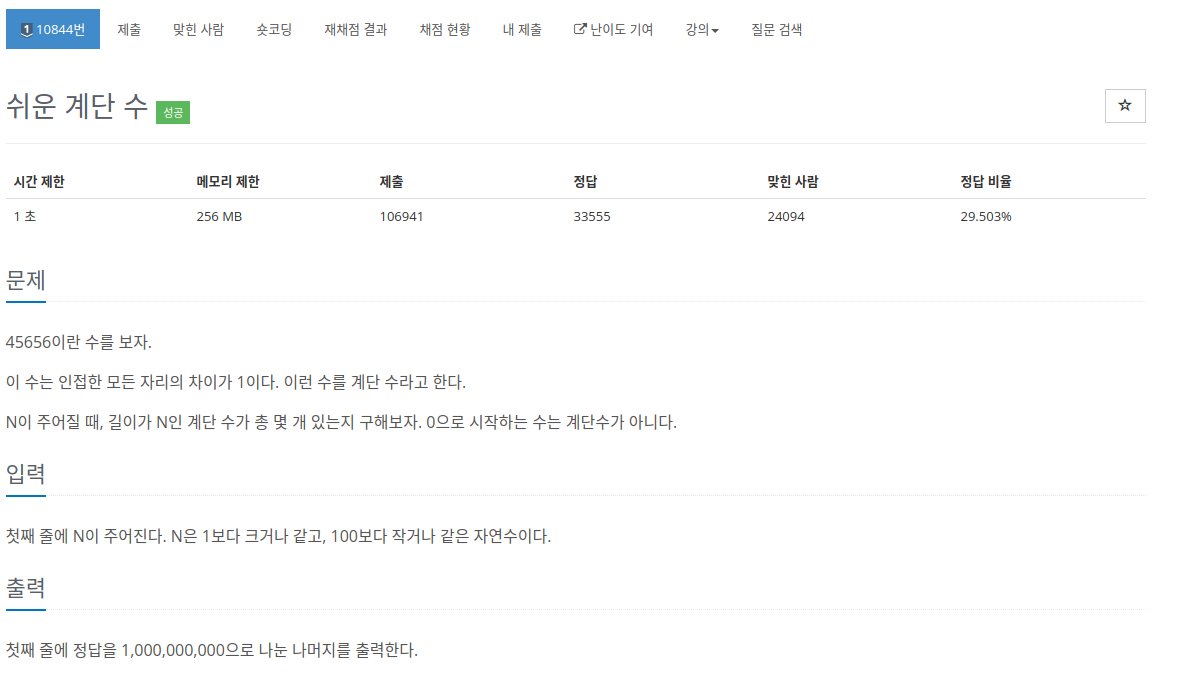
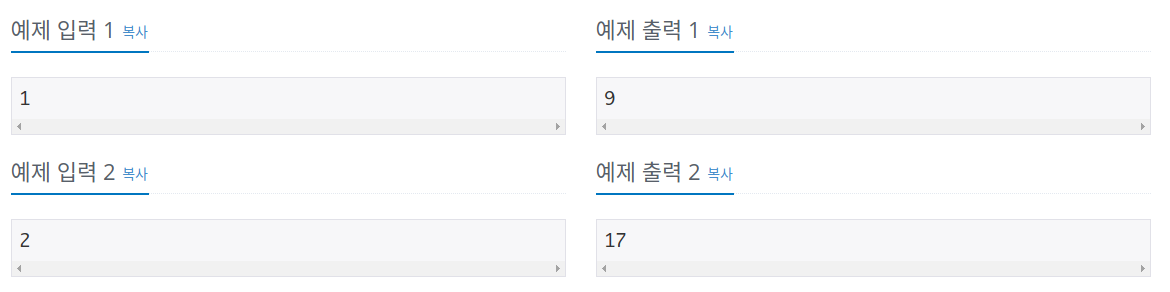
문제

풀이

먼저 이문제는 상당히 삽질하며 풀었던 문제이다. 1차원 리스트로 dp테이블을 만들어서 해결하려다가 정말 시간낭비를 많이했다.
먼저 이문제를 해결할때 생각순서는 이렇다.
모든 경우의 수에서 이 수가 계단수인지 검사하는 직관적으로 떠오르는 방법이 있는데
이방법을 할경우 연산횟수가 최대 2 ^100 개수의 숫자를 각 계단수인지 판별해야해서
무조건 시간초과가 발생할 것이고,

따라서 dp로 해결해 볼 수도 있을것이다.
그렇다면 내가 해결한 방식은 dp테이블을 1차원 테이블로 해서 해결하려다보니 해결방법이 쉽게 보이지 않아 2차원 테이블로 해보니

dp 테이블 d[i][j]는 j번째 자릿수가 숫자i인 계단수의 개수를 의미하고

점화식을 도출해보면

i가 1~8일경우에는 d[i][j] = d[i+1][j-1], d[i-1][j-1]이 될것이다.

왜냐하면!!
d[i][j]는 마지막 자리가 i인 계단수의 개수이므로 i와 1만 차이나는 경우만 숫자가 들어갈 수 있기 때문에 j-1자리의 수가 i + 1이거나 i-1일때의 계단수를 더해주면 d[i][j]가나오고

비슷한 논리로

i가 0일때는 d[0][j] = d[1][j-1]
i가 9일때는 d[9][j] = d[8][j-1]이 된다.

왜냐하면 i가 0이거나 9일때는 1씩차이나는 숫자가 각각 1개씩이기 때문이다.

따라서 이 점화식에 기반해 코드를 짜보면

코드

#입력
# 첫째 줄에 N이 주어진다. N은 1보다 크거나 같고, 100보다 작거나 같은 자연수이다.

#점화식
# dp[i][j]가 의미하는 것은 j번째 자리의 숫자가 i일때 가능한 계단수의 개수로 놓는다면

# i가 1~8일 때는 d[i][j] = d[i-1][j-1] + d[i+1][j-1]이된다 
# i가 0 일 때는 d[i][j] = d[i+1][j-1]
# i가 9 일 때는 d[i][j] = d[i-1][j-1]

N = int(input())

dp = [[0] * (N+1) for _ in range(10)]

for i in range(1,10):
  dp[i][1] = 1

for j in range(2, N+1):
  for i in range(10):
    if(i == 0):
      dp[i][j] = dp[1][j-1]
    elif(i == 9):
      dp[i][j] = dp[8][j-1]
    else:
      dp[i][j] = dp[i-1][j-1] + dp[i+1][j-1]

result = 0

for i in range(10):
  result += dp[i][N]
  
print(result % 1000000000)